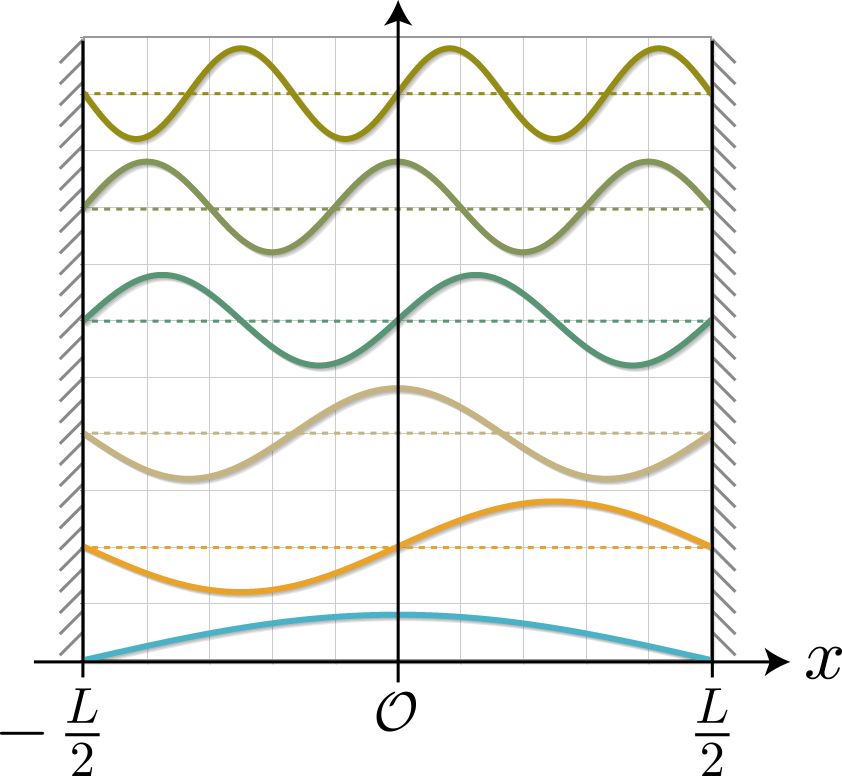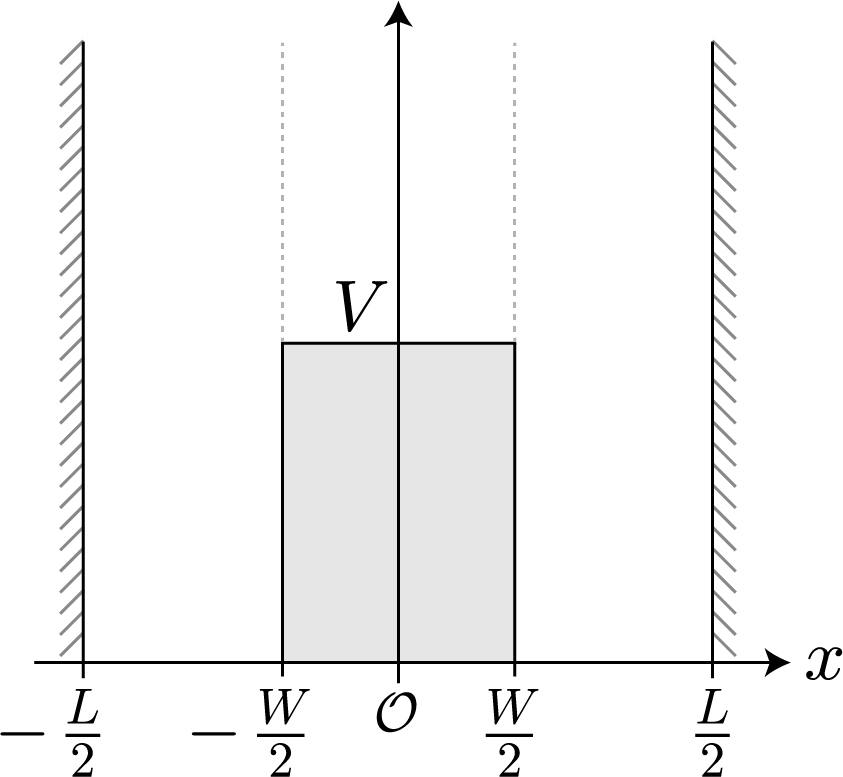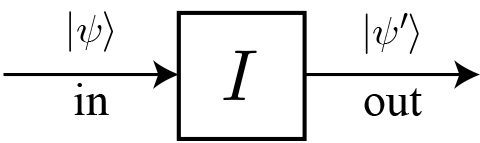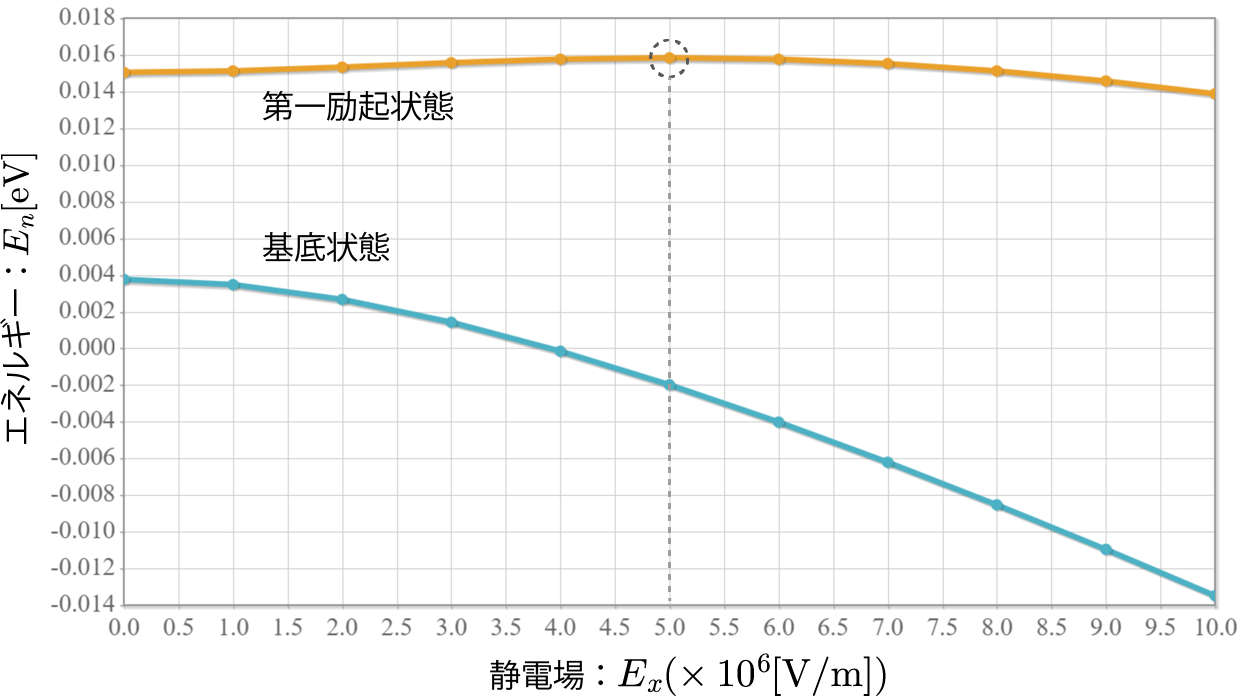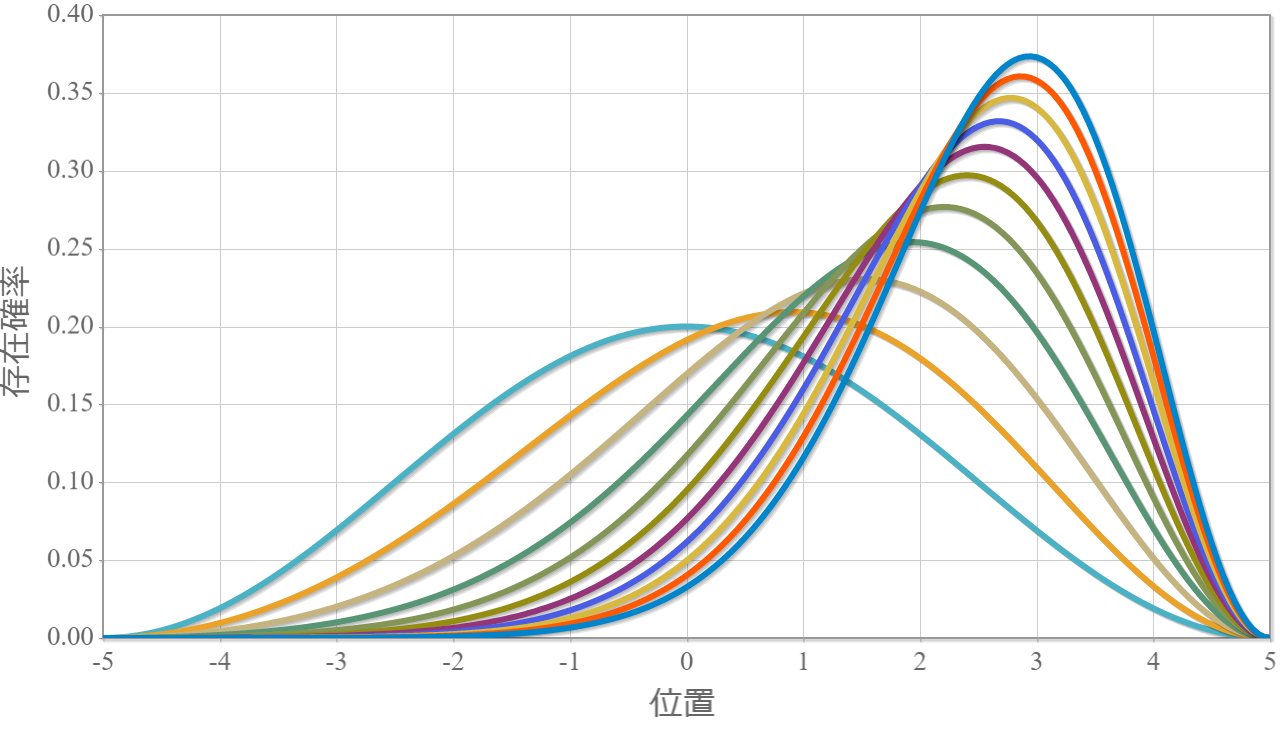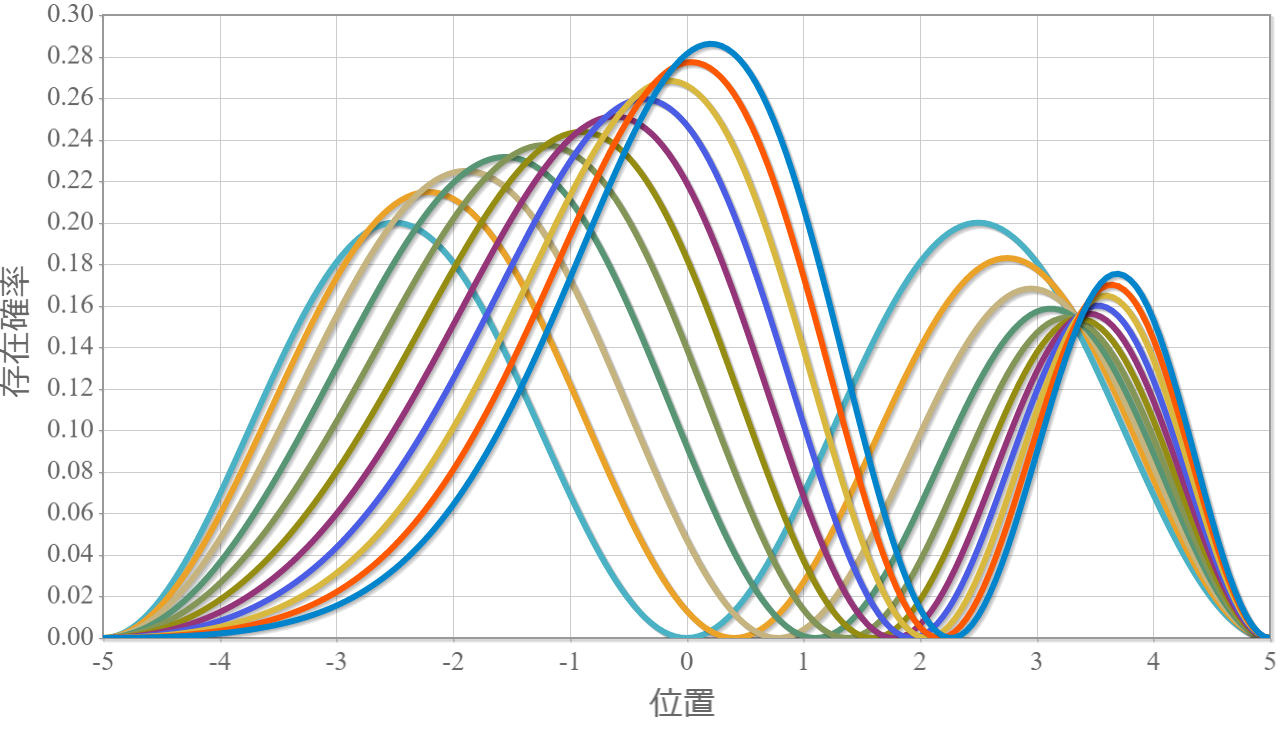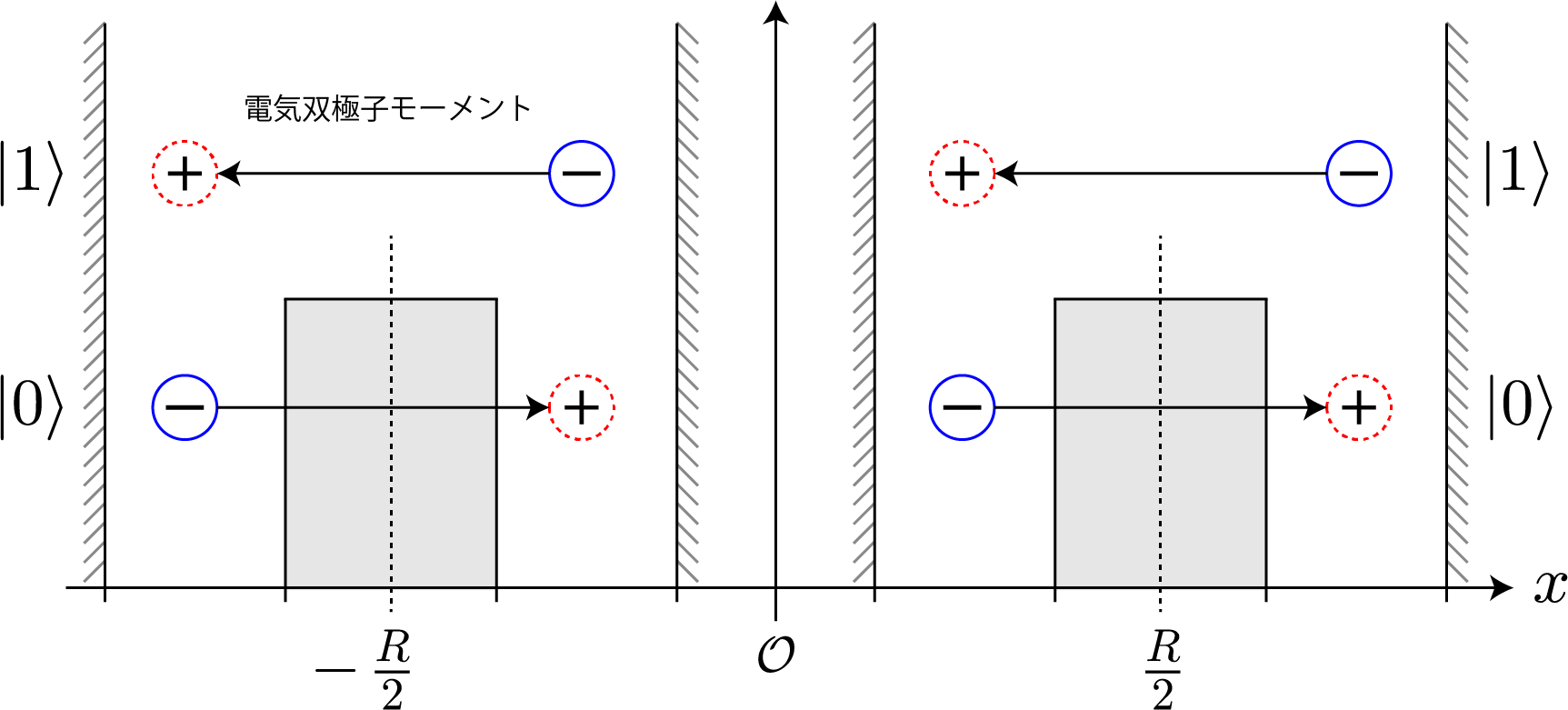
前回までで、1量子ビットを表現する量子井戸に束縛された電子の振る舞いを大体シミュレーションすることができたね。今回は、この量子井戸を2つ並べて2量子ビットとして利用するための表現方法と、2量子ビットの万能量子ゲートとして動作させるための動作原理についてまとめるよ。2量子ビットの表現を考える前にちょっと電磁気学の復習するよ。1つの量子ドットに束縛された電子に外部からx軸方向に静電場を加えた場合、電子が基底状態($| 0\rangle$)に存在する場合には電子は左に分布し、励起状態($| 1\rangle$)に存在する場合には電子は右に分布するんだったね(参照:(10)2重量子ドットに束縛された電子に静電場を加えたときの固有状態の計算結果)。この電子分布の偏りは第1次近似として次式で定義される電気双極子モーメント
\begin{align}
\boldsymbol{p}_E^{(1)} \equiv \int \boldsymbol{r}_1 \rho(\boldsymbol{r}_1) d\boldsymbol{r}_1 = \left\{ \matrix{ +\boldsymbol{p}_E & \cdots |0\rangle \cr -\boldsymbol{p}_E & \cdots|1\rangle }\right.
\end{align}
で表すことができるね。電気双極子モーメントは基底状態の場合は電気双極子が正の方向、励起状態の場合には負の方向に向くね。2つ目の量子井戸でも同様に
\begin{align}
\boldsymbol{p}_E^{(2)} &\ \equiv \int \boldsymbol{r}_2 \rho(\boldsymbol{r}_2) d\boldsymbol{r}_2 = \left\{ \matrix{ +\boldsymbol{p}_E & \cdots |0\rangle \cr -\boldsymbol{p}_E & \cdots|1\rangle }\right.
\end{align}
と表すことができるね。一般に2つの電気双極子モーメントが存在する場合、片方からもう片方への位置ベクトルを $\boldsymbol{R}$ として、相互作用によるポテンシャルエネルギーは
\begin{align}
U_E(\boldsymbol{R}) = \frac{1}{4\pi \epsilon_0}\, \frac{\boldsymbol{p}_E^{(1)}\cdot\boldsymbol{p}_E^{(2)}}{R^3} – \frac{3}{4\pi \epsilon_0}\, \frac{(\boldsymbol{p}_E^{(1)}\cdot\boldsymbol{R}) (\boldsymbol{p}_E^{(2)}\cdot\boldsymbol{R})}{R^5}
\end{align}
となるね。今回のように $\boldsymbol{R}$ の方向と電気双極子モーメントの向きが一直線の場合、
\begin{align}
U_E(R) = -\frac{1}{2\pi \epsilon_0}\, \frac{p_E^{(1)}p_E^{(2)}}{R^3} \equiv \mp \Delta U
\end{align}
となるので、電気双極子モーメントの向きが平行の場合には一致する場合にはエネルギーは $\Delta U$ 下がり、反対に向きが反平行の場合にエネルギーは $\Delta U$ 上がるね。この事実を用いて2量子ビットの量子ゲートを設計することができよ。
2量子ビットの量子状態の表現
1量子ビットの場合、量子井戸の基底状態と励起状態の固有関数の具体的な関数形は考えずに、それぞれケットを用いて $|0\rangle$ , $|1\rangle$ と表せることをはすでに解説したね。2量子ビットの場合、1つ目の「0」or「1」を第1量子ビットの状態、2つ目の「0」or「1」を第2量子ビットの状態として、$|0\rangle \otimes |0\rangle$ , $|0\rangle \otimes |1\rangle$ , $|1\rangle \otimes |0\rangle$ , $|1\rangle \otimes |1\rangle$ と表すことができるよ。「$\otimes$」は数学的には直積と呼ばれ、「$\otimes$」の前後の異なる座標系の状態をつなぐ役割を果たすよ。なお、「$\otimes$」を毎回書くのが煩わしい場合は、「$\otimes$」を省略して、$|00\rangle$, $|01\rangle$, $|10\rangle$, $|11\rangle$ とも表すよ。
電気双極子モーメント演算子と相互作用演算子
先に解説したとおり、量子井戸の基底状態と励起状態のどちらに存在するかによって、電気双極子モーメントの向きが異なるね。状態 $|0\rangle$ と $|1\rangle$ に作用する電気双極子モーメント演算子 $\hat{\boldsymbol{p}}_E$ を次のように定義するよ。
\begin{align}
\hat{\boldsymbol{p}}_E |0\rangle &\ = +\boldsymbol{p}_E |0\rangle \\
\hat{\boldsymbol{p}}_E |1\rangle &\ = -\boldsymbol{p}_E |1\rangle
\end{align}
この電気双極子モーメント演算子は2つの量子井戸の電子それぞれ個別に作用するので、先の2量子ビットの量子状態の表現を用いると
\begin{align}
\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E |00\rangle &\ = +\boldsymbol{p}_E^2 |00\rangle \\
\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E |01\rangle &\ = -\boldsymbol{p}_E^2 |01\rangle \\
\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E |10\rangle &\ = -\boldsymbol{p}_E^2 |10\rangle \\
\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E |11\rangle &\ = +\boldsymbol{p}_E^2 |11\rangle \\
\end{align}
と計算することができるよ。つまり、電気双極子モーメント同士の相互作用を表す演算子 $V_E$は
\begin{align}
V_E = -\frac{1}{2\pi \epsilon_0}\, \frac{\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E}{R^3}
\end{align}
と表すことができるね。
2量子ビットのハミルトニアン
電気双極子モーメントの相互作用演算子を定義できたので、あとはそれぞれの量子井戸の電子単体のハミルトニアンを考えるだけだね。$\hat{H}_1$ と $\hat{H}_2$ はそれぞれの量子井戸中の電子に静電場が加えられたときのハミルトニアンとして、第1量子ビットと第2量子ビットの基底状態エネルギーをそれぞれ $E_1^{(0)}$ と $E_2^{(0)}$、励起状態のエネルギーをそれぞれ $E_1^{(1)}$ と $E_2^{(1)}$ と表した場合、次のような固有状態とあらすことができるね。
\begin{align}
(\hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 ) |00\rangle &\ = (E_1^{(0)} + E_2^{(0)}) |00\rangle\\
(\hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 ) |10\rangle &\ = (E_1^{(1)} + E_2^{(0)}) |10\rangle\\
(\hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 ) |01\rangle &\ = (E_1^{(0)} + E_2^{(1)}) |01\rangle\\
(\hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 ) |11\rangle &\ = (E_1^{(1)} + E_2^{(1)}) |11\rangle
\end{align}
このハミルトニアンに先の電気双極子モーメントの相互作用演算子を加えると、ハミルトニアン $\hat {H}$ が完成するね。
\begin{align}
\hat {H} &\ = \hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 + \hat{V}_E \\
\hat{V}_E &\ = -\frac{1}{2\pi \epsilon_0}\, \frac{\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E}{R^3}
\end{align}
2量子ビットの量子状態はこのハミルトニアンの固有状態となっているよ。
\begin{align}
\hat {H} |00\rangle &\ = (E_1^{(0)} + E_2^{(0)} – \Delta U_E) |00\rangle\\
\hat {H} |10\rangle &\ = (E_1^{(1)} + E_2^{(0)} + \Delta U_E) |10\rangle\\
\hat {H} |01\rangle &\ = (E_1^{(0)} + E_2^{(1)} + \Delta U_E) |01\rangle\\
\hat {H} |11\rangle &\ = (E_1^{(1)} + E_2^{(1)} – \Delta U_E) |11\rangle
\end{align}
2量子ビット万能量子ゲートについて
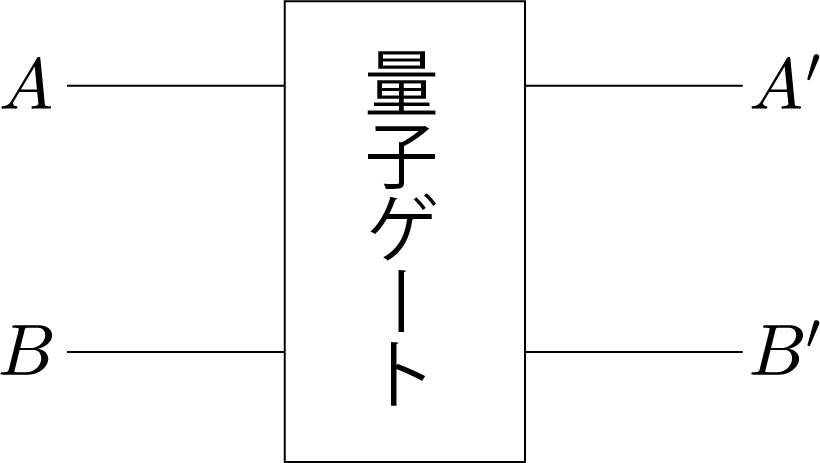
2量子ビット量子ゲートとは、2つの量子ビットの状態を入力とし、変化した2つの量子ビットの状態を出力とみなす素子を抽象化した表現だよ。右図のAとBが入力前の量子ビットの状態を表していて、A’とB’が変化後の量子ビットの状態を表しているよ。A, B, A’, B’ はそれぞれ $|0\rangle$ と $|1\rangle$ の任意の重ね合わせで与えられるよ。このような2量子ビット量子ゲートで最も重要なのは、A, B, A’, B’ の関係が下の真理値表で表される「制御・NOT演算(CNOT)ゲート」と呼ばれる量子ゲートだよ。
| A | B |
|---|---|
| 0 | 0 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
| A’ | B’ |
|---|---|
| 0 | 0 |
| 0 | 1 |
| 1 | 1 |
| 1 | 0 |
制御・NOT演算ゲートは、入力Aが $0$ の場合はBには何の変化もなく、入力 A が $1$ の場合は入力された B のビットを反転(NOT演算)させるよ。論理式で表すと
\begin{align}
A’&\ =A\\
B’&\ = A \otimes B
\end{align}
となるよ。この場合の「$\otimes$」は排他的論理和を表す記号で、先の直積とは違う意味だよ。そして実は、制御・NOT演算ゲートは複数組み合わせることで2量子ビットで構成される論理ゲートをすべて表現することができるんだよ!そのため、制御・NOT演算ゲートは2量子ビットの万能量子ゲートとも呼ばれるよ。2量子ビットの状態をケットベクトル
\begin{align}
|00\rangle = \left( \matrix{ 1\cr 0 \cr 0 \cr 0} \right) , |01\rangle = \left( \matrix{ 0\cr 1 \cr 0 \cr 0} \right), |10\rangle = \left( \matrix{ 0\cr 0 \cr 1 \cr 0} \right) , |11\rangle = \left( \matrix{ 0\cr 0 \cr 0 \cr 1} \right)
\end{align}
で表した場合、制御・NOT演算ゲート(CNOT)は
\begin{align}
{ \rm CNOT} = \left( \matrix{ 1& 0& 0&0 \cr 0&1 &0 & 0 \cr 0 & 0 & 0 & 1 \cr 0 & 0 &1& 0} \right)
\end{align}
と表すことができるね。実際に上記の真理値表を満たしていることが確認できるね。
\begin{align}
{\rm CNOT} |00\rangle &\ = |00\rangle\\
{\rm CNOT} |01\rangle &\ = |01\rangle\\
{\rm CNOT} |10\rangle &\ = |11\rangle\\
{\rm CNOT} |11\rangle &\ = |10\rangle\\
\end{align}
制御・NOT演算ゲートの動作原理
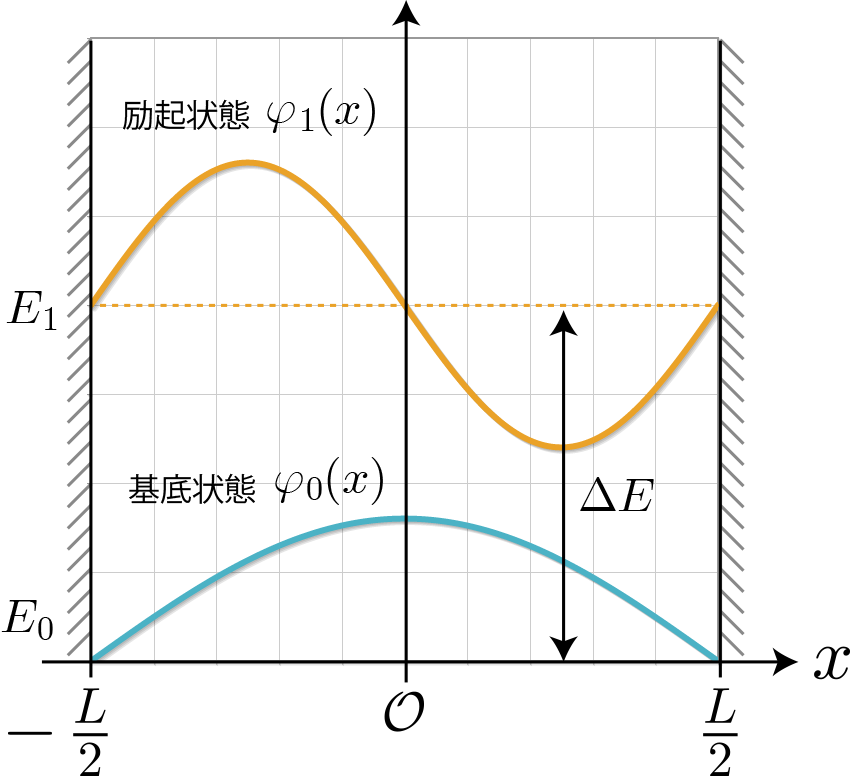
次に2量子ビット万能量子ゲートである制御・NOT演算ゲートを、2つの量子井戸を用いて具体的にどのようにして作ることができるのか解説するよ。本稿の前半で示したとおり、静電場が加えられた量子井戸中の電子は、基底状態($|0\rangle$)と励起状態($|1\rangle$)で異なる向きの電気双極子モーメントをもつので、相互作用の結果、第1量子井戸の電子状態が $|0\rangle$ か $|1\rangle$ によって、第2量子井戸の基底状態のと励起状態のエネルギー準位は変化するね。具体的には、第1量子井戸の電子状態が $|0\rangle$ の場合には第2量子井戸のエネルギーギャップは広がり、反対に第1量子井戸の電子状態が $|1\rangle$ の場合には第2量子井戸のエネルギーギャップは狭まるね。次の図はその模式図だよ。
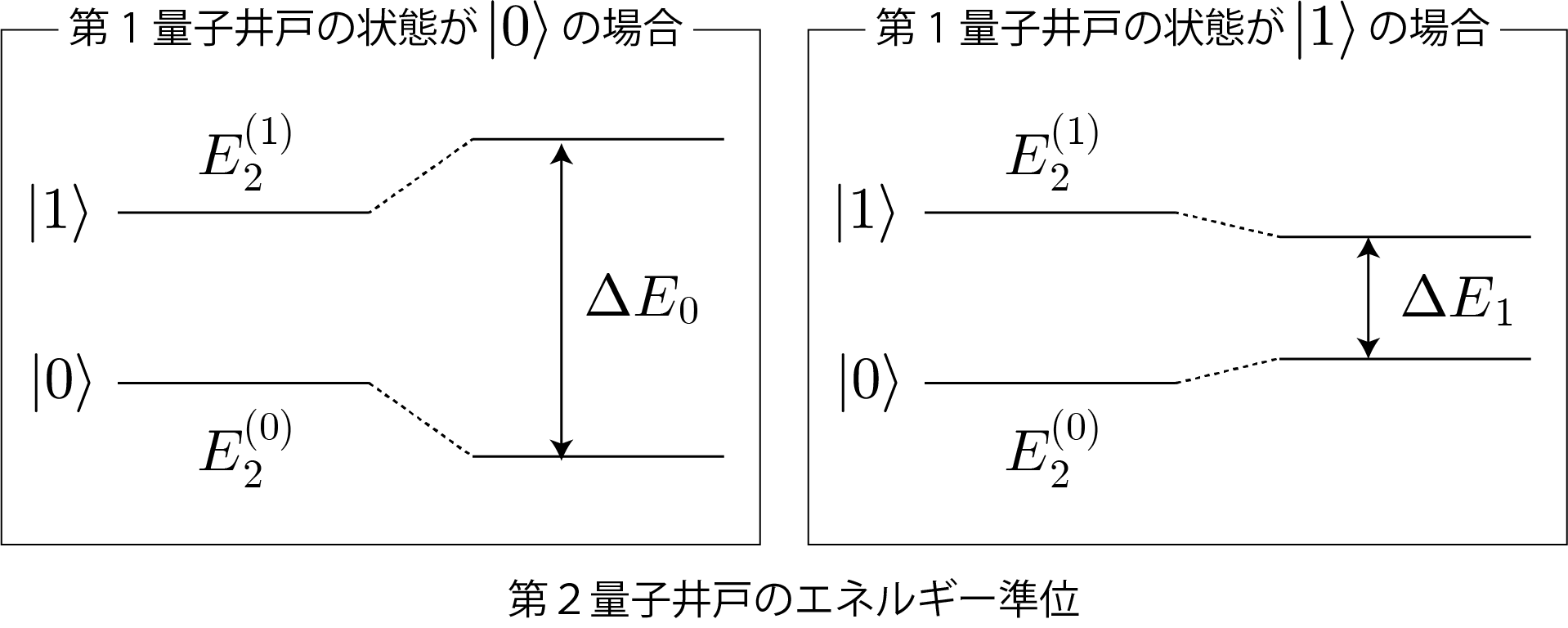
一方、エネルギーギャップに対応する電磁波を入射すると、これまでに何度か示したラビ振動を引き起こすことができるんだったね。つまり、狭まったエネルギーギャップ($\Delta E_2$)に相当する電磁波を入射すると、第1量子井戸の電子状態が $|0\rangle$ の場合には変化しないけれども、第1量子井戸の電子状態が $|0\rangle$ の場合には第2量子井戸の状態をラビ振動させることができるので、入射時間を適切にコントロールすることで、制御・NOT演算ゲートと同じ動作をさせることができるね。
制御・NOT演算ゲートに対応するハミルトニアンと計算方法
以上から2つの量子井戸に束縛された電子を量子ビットとして用いた場合の制御・NOT演算ゲートに対応するハミルトニアンは次のような式に与えられる。
\begin{align}
\hat{H} = \hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes \hat{H}_2 + \hat{V}_E + \boldsymbol{1} \otimes \hat{V}_A(t)
\end{align}
$\hat{H}_1$ と $\hat{H}_2$ は電子の運動エネルギーと外部静電場によるポテンシャル項をあわせたもの、$\hat{V}_E$ は電気双極子モーメントによる相互作用項、$\hat{V}_A(t)$ は第2量子井戸に入射する電磁波との相互作用項だよ。この内、時間に依存する項は最後の $\hat{V}_A(t)$ だけだね。実際にシミュレーションするには、任意の状態 $\psi(t)\langle$ を
\begin{align}
|\psi(t)\rangle = a_{00}(t)|00\rangle + a_{01}(t)|01\rangle + a_{10}(t)|10\rangle + a_{11}(t)|11\rangle \equiv \sum\limits_{n=0} a_n (t) |n\rangle
\end{align}
と展開しておいて、時間に依存するシュレーディンガー方程式
\begin{align}
i\hbar \frac{d}{dt}|\psi(t)\rangle = \hat{H}|\psi(t)\rangle
\end{align}
に代入して、左から $\langle m |$ を掛けて得られる連立微分方程式
\begin{align}
i\hbar \frac{d a_{m}(t)}{dt} \, = \sum\limits_{n=0} \langle m |\hat{H}|n\rangle a_n(t)
\end{align}
を計算すればいいね。次回は実際に計算を行うけれども、その前に上記のハミルトニアンは重要な近似がなされているのがちょっと気になるね。というのも、2つの電子同士の相互作用を電気双極子モーメントの相互作用だけを取り込んでいる点が不満だね。やはりできるだけ第一原理的にやりたいので、$V_E$ をクーロンポテンシャル
\begin{align}
\hat{V}_E = \frac{1}{4\pi \epsilon_0}\, \frac{1}{|x_1 – x_2|}
\end{align}
として、まずは2つの量子井戸の電子相互作用を踏まえた固有状態を計算してみるね。