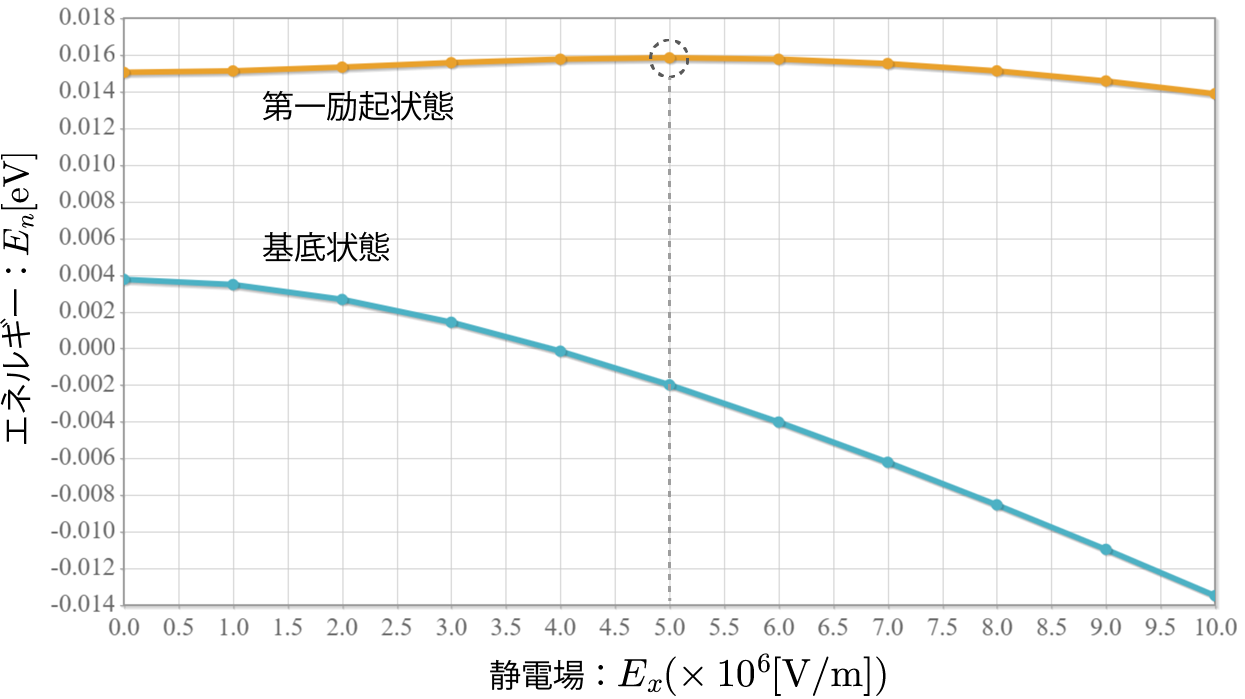
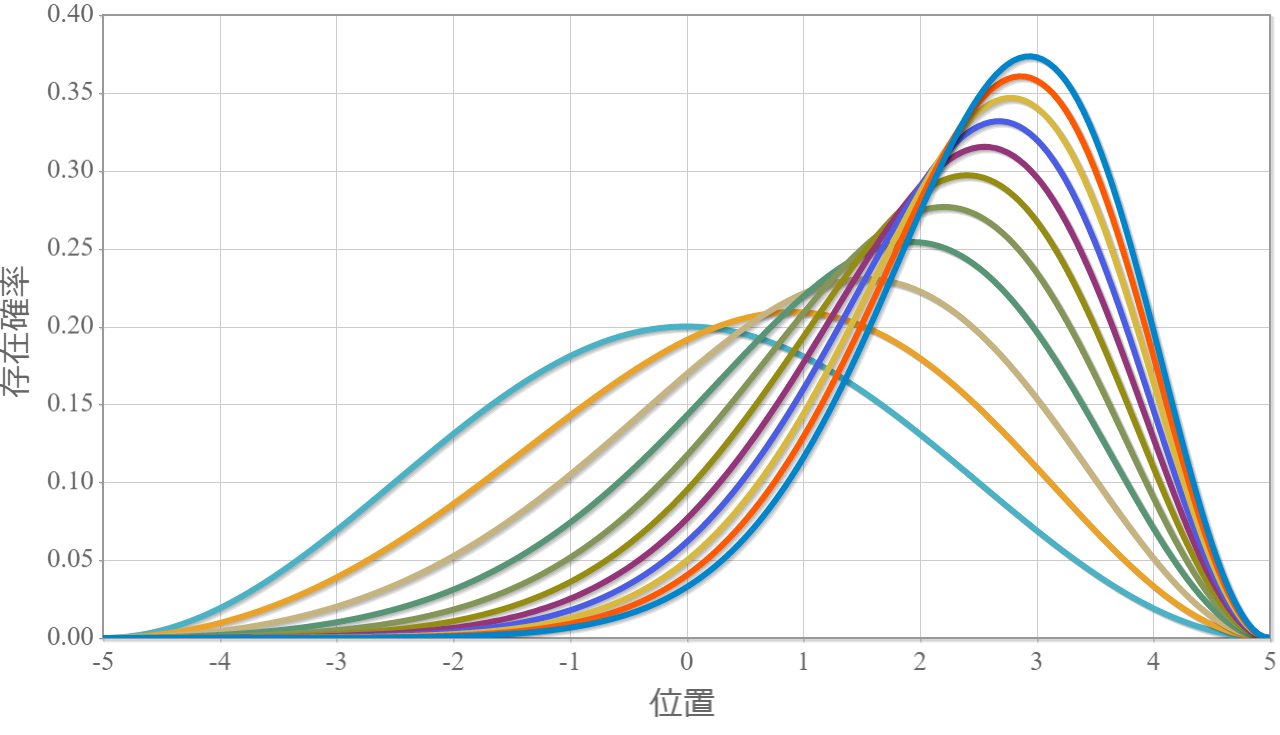
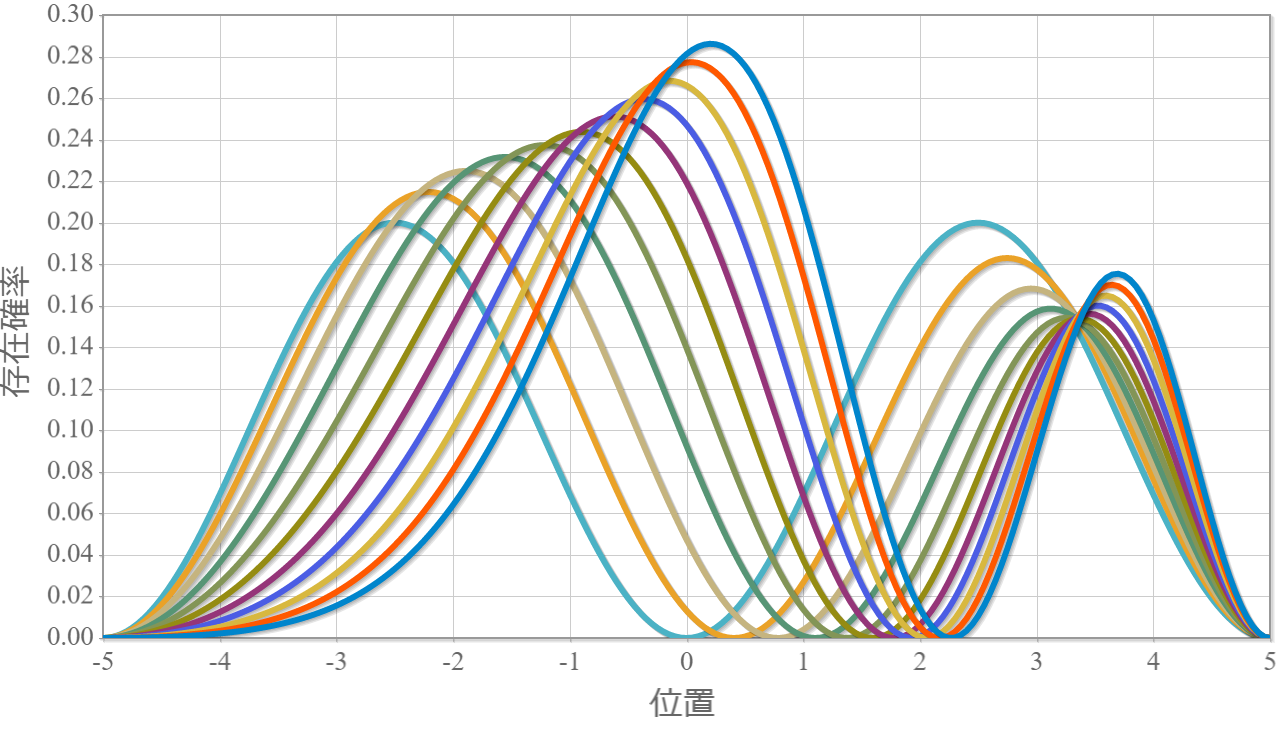
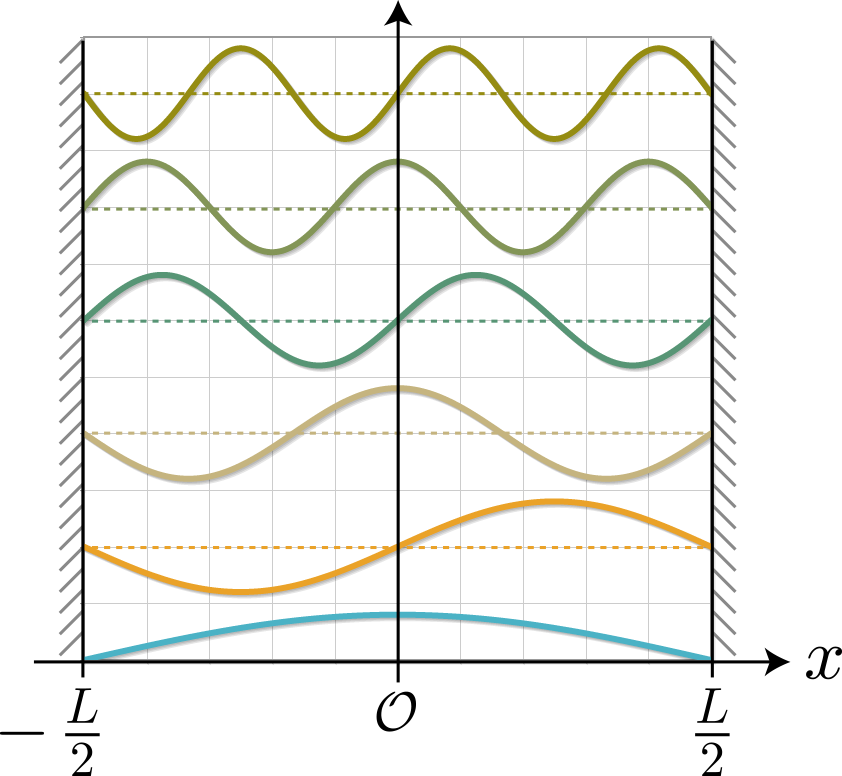
今度は静電場の代わりに、量子ドットに束縛された電子に電磁波(直線偏光)を外部から与えて、基底状態と第一励起状態との間のラビ振動を確認するよ。電磁波を表すベクトルポテンシャルを $\boldsymbol{A}$ とした場合のハミルトニアンは次のとおりだね(参考)。
\begin{align}
\hat{H} = \hat{H}_0 + \hat{V}(t) = -\frac{\hbar^2}{2m_e} \frac{d^2}{dx^2} + \frac{e}{m_e} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}
\end{align}
今回は1次元系で考えているので、ベクトルポテンシャルを $\boldsymbol{A}(t) = (A_x(t), 0, 0)$ として、
\begin{align}
A_x(t) = A_0 \cos(kx-\omega t)
\end{align}
と考えるよ。そして、このハミルトニアンの固有関数を外場が無いときの固有関数
\begin{align}
\varphi_n(x) = \sqrt{\frac{2}{L}} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ E_n = \frac{\hbar^2 k_n^2}{2m_e} \ , \
k_n = \frac{\pi(n+1)}{L}
\end{align}
で展開して、その係数の値が時間に依存するとして展開するよ。
\begin{align}
\psi(x, t) = \sum\limits_{n=0} a_n(t) \varphi_n(x)
\end{align}
これを時間依存を考慮したシュレーディンガー方程式
\begin{align}
i \hbar \frac{\partial }{\partial t} \psi(x, t) = \hat{H} \psi(x, t)
\end{align}
に代入して、両辺に $\varphi^*_m(x)$ を掛けて全空間で積分するよ。すると、$a_m(t)$ に関する連立常微分方程式が得られるね。
\begin{align}
i \hbar \frac{d a_m(t)}{d t} = E^{(0)}_m a_m(t) + \sum\limits_{n=0} \langle m | \hat{V}(t) | n \rangle a_n(t)
\end{align}
$\langle m | \hat{V}(t) | n \rangle$ は、$\hat{p}_x/m_e = [\hat{H}_0, x ]/i\hbar$ を考慮すると
\begin{align}
\langle m | \hat{V}(t) | n \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_m(x) \hat{V}(t)
\varphi_n(x)\, dx = \frac{eA_0}{m_e} \langle m | \cos(kx-\omega t) p_x | n \rangle = \frac{eA_0}{i\hbar} \langle m | \cos(kx-\omega t) [\hat{H}_0, x ] | n \rangle
\end{align}
と変形できて、波長が量子ドットのサイズよりも十分大きいと仮定すると、$kx \simeq 0$ と近似することができるので
\begin{align}
\langle m | \hat{V}(t) | n \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) \left[ E^{(0)}_m – E^{(0)}_n \right] \langle m |
x | n \rangle
\end{align}
となるので、$a_m(t)$ に関する連立常微分方程式は
\begin{align}
i \hbar \frac{d a_m(t)}{d t} = E^{(0)}_m a_m(t) + \frac{eA_0}{i\hbar} \cos(\omega t)\sum\limits_{n=0} \left[ E^{(0)}_m – E^{(0)}_n \right] \langle m | x | n \rangle a_n(t)
\end{align}
となるね。$\langle m |x | n \rangle $ は時間に依存しないので、一度計算するだけでいいね。電磁波の角振動数が2準位間のエネルギー差 $\Delta E$ と表して $\omega = \Delta E / \hbar$ となるときに、2準位間を周期的に遷移するね。次回はこれをシミュレーションするよ。