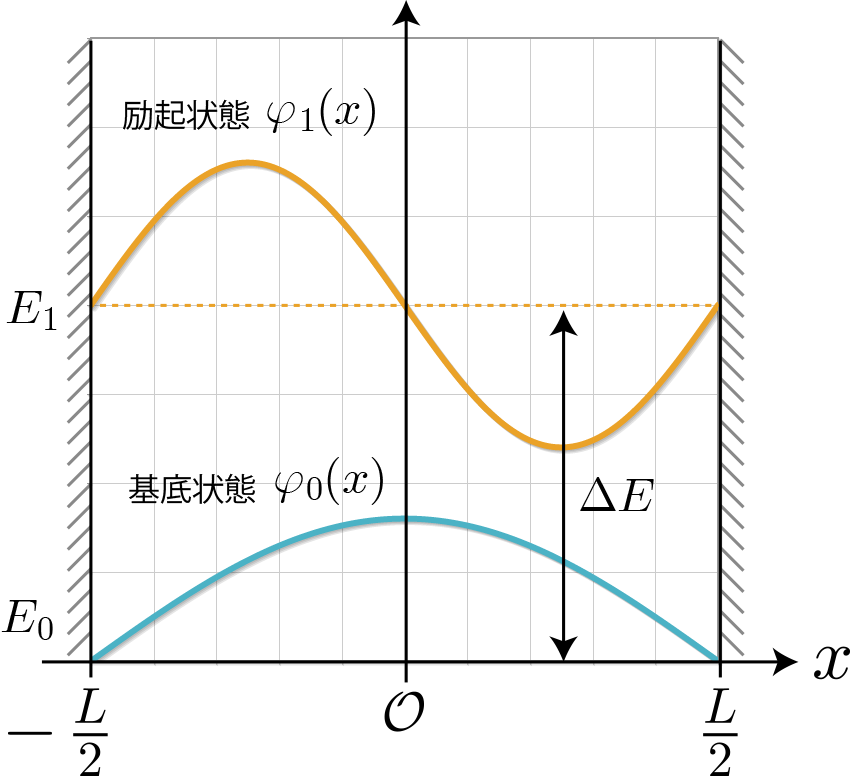
本シリーズは、右図のような量子ドットに束縛された電子の基底状態(固有関数:$\varphi_0(x)$、固有エネルギー:$E_0$)と第一励起状態(固有関数:$\varphi_1(x)$、固有エネルギー:$E_1$)の2準位を量子ビットとみなした計算機である、量子ドット量子コンピュータの動作をシミュレーションするよ。本稿では、この量子ドット型の量子ビットの表現と操作方法を解説するよ。
量子ドット型の量子ビットの表現
量子ドット型の量子ビットは、電子が基底状態に存在する状態と励起状態に存在する状態が重なり合った状態で表現されるよ。時間依存性まで考慮すると具体的には
\begin{align}
\psi(x,t) = a_0(t) \varphi_0(x) + a_1(t) \varphi_1(x)
\end{align}
と表されるね。$a_0(t)$ と $a_1(t)$ は基底状態と励起状態の重ね合わせの度合いを表わす複素数で、$|a_0(t)|^2$ と $|a_1(t)|^2$ がそれぞれの状態に存在する確率を表すよ。 この $a_0(t)$ と $a_1(t)$ は基底状態と励起状態はエネルギーから決まる角振動数 $\omega_0$ と $\omega_1$ で
\begin{align}
a_0(t) = a_0 e^{-i\omega_0 t} \ , \ a_1(t) = a_1 e^{-i\omega_1 t}
\end{align}
という感じで単振動しているよ。ちなみに各準位の角振動数はエネルギーと $\omega_0 = E_0 / \hbar$、 $\omega_1 = E_1 / \hbar$ の関係があるよ。基底状態と励起状態の角振動数が異なるので、時間が経過するに連れて位相差(位相比?)が生じるね。後で解説するけれども、
\begin{align}
\psi(x,t) = e^{-i\omega_0 t} \left[ a_0 \varphi_0(x) + a_1\varphi_1(x)e^{-i\omega_{01} t} \right]
\end{align}
この位相差の重要になるよ($\omega_{01} \equiv \omega_{1}-\omega_{0} $)。上記の量子ビットの表記は、量子ドットの固有関数を用いているけれども、量子ビットそのものは様々な系で実現することができるので、一般的にはブラ・ケット表記を用いて、2つの量子状態を $| 0 \rangle , | 1 \rangle$ と抽象的に表現するね。これに倣えば、
\begin{align}
| \psi(t) \rangle = a_0 (t) | 0 \rangle + a_1 (t) | 1 \rangle
\end{align}
と表されるね。今後、量子ビットを表す場合にはこちらの表記を用いるよ。ちなみに、この $| 0 \rangle, | 1 \rangle$ と $\varphi_0(x), \varphi_1(x)$ とは $ \varphi_0(x) = \langle x | 0 \rangle , \varphi_1(x) = \langle x | 1 \rangle$ という関係があるよ。
1量子ビットの基本量子ゲート
量子ビットを制御するための操作は量子ゲートと呼ばれるよ。この量子ゲートは、量子力学的には量子状態に対してユニタリー変換を施すことに対応するよ。このユニタリ変換は、固有状態を縦ベクトルで表現したときに正方行列で表すことができるよ。$|0 \rangle$ と $|1 \rangle$ を要素数2個の縦ベクトル
\begin{align}
| 0 \rangle = \left( \matrix{ 1 \cr 0} \right) \ , \ | 1 \rangle = \left( \matrix{ 0 \cr 1} \right)
\end{align}
で表わすと、1量子ビットは
\begin{align}
| \psi \rangle = a_0 | 0 \rangle + a_1 | 1 \rangle = a_0 \left( \matrix{ 1 \cr 0} \right) + a_1 \left( \matrix{ 0 \cr 1} \right) = \left( \matrix{ a_0 \cr a_1} \right)
\end{align}
と表すことができて、ユニタリー変換はユニタリー行列と呼ばれる2×2の行列で表現ことができるよ。量子ゲートを表すユニタリー行列の例は次のとおりだよ。
恒等ゲート $I$
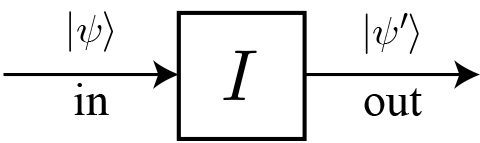
恒等ゲート $I$ は、入力状態と出力状態が同じとなる量子ゲートで、行列は単位行列で表されるよ。
\begin{align}
I = \left( \matrix{ 1 & 0 \cr 0 & 1} \right)
\end{align}
もちろん、量子ゲート通過後の状態 $| \psi’ \rangle$ は、通過前の状態 $| \psi \rangle$ と一致するよ。
\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \left( \matrix{ 1 & 0 \cr 0 & 1} \right) \left( \matrix{ a_0 \cr a_1} \right)= \left( \matrix{ a_0 \cr a_1} \right)
\end{align}
否定ゲート $X$
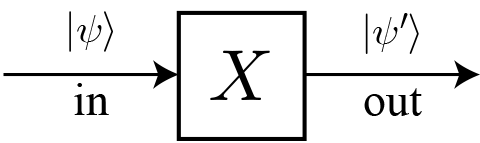
否定ゲート $X$ は、量子ビットの状態を反転させる量子ゲートで、行列は次のように表されるよ。
\begin{align}
X = \left( \matrix{ 0 & 1 \cr 1 & 0} \right)
\end{align}
次の計算でわかる通り、量子ゲートを通過すると行列要素が反転していることが分かるね。
\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \left( \matrix{ 0 & 1 \cr 1 & 0} \right)\left( \matrix{ a_0 \cr a_1} \right) = \left( \matrix{ a_1 \cr a_0} \right)
\end{align}
この量子ゲートは、外部から特定の振動数の電磁波を特定時間与えることで生じるエネルギー準位間の遷移で実現することができるよ。
位相シフトゲート $P_{\theta}$
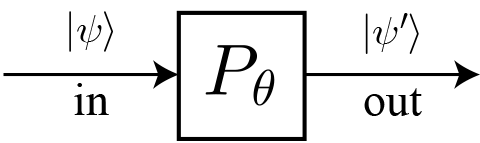
位相シフトゲート $P_{\theta}$ は、量子ビットの2つの状態の相対的な位相をずらす量子ゲートで、行列は次のように表されるよ。
\begin{align}
P_{\theta} = \left( \matrix{ 1 & 0 \cr 0 & e^{i\theta}} \right)
\end{align}
次の計算でわかる通り、量子ゲートを通過すると $a_1$ に位相因子 $e^{i\theta}$ が掛かるよ。
\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \left( \matrix{ 1 & 0 \cr 0 & e^{i\theta}} \right) \left( \matrix{ a_0 \cr a_1} \right) =
\left( \matrix{ a_0 \cr a_1e^{i\theta}} \right)
\end{align}
この量子ゲートは、先に示したとおり、異なるエネルギー状態で振動数が違うことを考慮すると、特定時間だけ放っておくことで実現することができるよ。
アダマールゲート $H$
アダマールゲート $H$ は、量子ビットの回転を表す量子ゲートで、行列は次のように表されるよ。
\begin{align}
H = \frac{1}{\sqrt{2}} \left( \matrix{ 1 & 1 \cr 1 & -1 }\right)
\end{align}
次の計算でわかる通り、量子ゲートを通過すると、等しい重みで混合されるよ。$H^2 = I$ となるので、アダマールゲートは2回通すと元にもどるね。
\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \frac{1}{\sqrt{2}} \left( \matrix{ 1 & 1 \cr 1 & -1 }\right) \left( \matrix{ a_0 \cr a_1} \right) =\frac{1}{\sqrt{2}} \left( \matrix{ a_0 + a_1 \cr a_0 – a_1} \right)
\end{align}
このゲートの重要性を示す一例として、入力状態が $a_0 = 1 , a_1 =0$ (100% $| 0 \rangle$ 状態 )とすると、
\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \frac{1}{\sqrt{2}} \left( \matrix{ 1 & 1 \cr 1 & -1 }\right) \left( \matrix{
1 \cr 0} \right) =\frac{1}{\sqrt{2}} \left( \matrix{ 1 \cr 1} \right)
\end{align}
となり、均等に混合した状態($| 0 \rangle$ と $| 1 \rangle$ が50%ずつの状態 )を作り出すことができるね。
なお、この量子ゲートも外部からの特定の振動数の電磁波を特定時間与えることで生じるエネルギー準位間の遷移で実現することができるよ。
1量子ビットの万能量子ゲート
まず、任意の1量子ビットの状態は
\begin{align}
| \psi \rangle = e^{i\gamma } \left[ \cos\frac{\theta}{2} | 0 \rangle + \sin\frac{\theta}{2} e^{i\phi} | 1 \rangle \right]
\end{align}
で表されることが知られているよ($ 0 \leq \theta \leq \pi \ , \ 0 \leq \phi \leq 2\pi $)。ただし、全体に掛かる因子 $e^{i\gamma}$ は観測には掛からないので無視できるので、
\begin{align}
| \psi \rangle = \cos\frac{\theta}{2} | 0 \rangle + \sin\frac{\theta}{2} e^{i\phi} | 1 \rangle
\end{align}
ですべての状態を表しているよ。この状態を生み出すことのできる量子ゲートは「1量子ビットの万能量子ゲート」と呼ばれるよ。このゲートはアダマールゲート $H$ と 位相シフトゲート $P_{\theta}$ の2つを組み合わせることで作ることができるよ。例えば、初期状態として $ | \psi \rangle =| 0 \rangle $ から任意の状態を生成するには、
\begin{align}
U = P_{\phi+\frac{\pi}{2}} H P_{\theta} H
\end{align}
という演算で実現することができるよ。実際に確かめてみよう。
\begin{align}
| \psi’ \rangle &\ = P_{\phi+\frac{\pi}{2}} H P_{\theta} H | 0 \rangle = P_{\phi+\frac{\pi}{2}} H P_{\theta} \frac{ | 0 \rangle + | 1 \rangle }{\sqrt{2}} = P_{\phi+\frac{\pi}{2}} H \frac{ | 0 \rangle + e^{i\theta}| 1 \rangle }{\sqrt{2}}\\
&\ = P_{\phi+\frac{\pi}{2}} \frac{ (1+e^{i\theta})| 0 \rangle + (1-e^{i\theta})| 1 \rangle }{2} = \frac{ (1+e^{i\theta})| 0 \rangle + (1-e^{i\theta}) e^{i\phi+i\frac{\pi}{2}}| 1 \rangle }{2}\\
&\ = e^{i\frac{\theta}{2}} \frac{ (e^{-i\frac{\theta}{2}}+e^{i\frac{\theta}{2}})| 0 \rangle + i(e^{-i\frac{\theta}{2}}-e^{i\frac{\theta}{2}}) e^{i\phi}| 1 \rangle }{2} \\
&\ = e^{i\frac{\theta}{2}}\left[ \cos\frac{\theta}{2} | 0 \rangle+ \sin\frac{\theta}{2} e^{i\phi}| 1 \rangle \right]
\end{align}
ちゃんとなってるね。以上で1量子ビットについての解説は終わりだよ。まだ1量子ビットなのでこれ単体ではコンピュータとして何の演算もできないね。2量子ビットについての解説は、1量子ビットの物理的操作方法をマスターした後に改めて解説するよ。
