任意の電磁場中を運動する電子のハミルトニアンは「静磁場が加わる場合のハミルトニアンを復習しよう!」で示したとおりだね。ベクトルポテンシャルを $\boldsymbol{A}$、スカラーポテンシャルを $\phi$ とした場合、
\begin{align}
\hat{H} = \frac{1}{2m_e} (\hat{\boldsymbol{p}} + e \boldsymbol{A})^2 -e \phi
\end{align}
となるね。水素原子に束縛された電子を考えると、クーロンゲージを採用して
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \boldsymbol{p} + \frac{e^2 \boldsymbol{A}^2}{2m_e}
\end{align}
となるね。$\hat{H}_0$ は外場が無い場合の水素原子に束縛された電子のハミルトニアン
\begin{align}
\hat{H}_0 = \frac{\hat{\boldsymbol{p}}^2}{2m_e} – \frac{e^2}{ 4\pi\epsilon_0} \, \frac{1}{r}
\end{align}
だよ。電磁波の場合には、このベクトルポテンシャル $\boldsymbol{A}(t)$ が時間に依存するんだね。さらに、スピンも考慮するならば、スピンのゼーマン項を加えて
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \boldsymbol{p} + \frac{e}{m_e} \hat{\boldsymbol{S}}\cdot \boldsymbol{B} + \frac{e^2 \boldsymbol{A}^2}{2m_e}
\end{align}
だね。今回、電磁波の進行方向をx軸として、磁場成分をy軸、電場成分をz軸となるように、ベクトルポテンシャルを
\begin{align}
\boldsymbol{A} = \left(0, 0, A_0 \cos(kx-\omega t) \right)
\end{align}
と与えると、電場と磁場は次のようになるね。
\begin{align}
\boldsymbol{E} &\ = -\frac{\partial \boldsymbol{A}}{\partial t} =\left(0, 0, – \omega A_0 \sin(kx-\omega t) \right)\\
\boldsymbol{B} &\ = \nabla \times \boldsymbol{A} =\left(0, k A_0 \sin(kx-\omega t), 0 \right)
\end{align}
電磁波による状態遷移の数値計算
電子の状態遷移を議論するには、時間に依存したシュレディンガー方程式
\begin{align}
i\hbar\frac{\partial}{\partial t} \psi(\boldsymbol{r}, t) = \hat{H} \psi(\boldsymbol{r}, t)
\end{align}
を解けばいいんだね。まずは波動関数 $\psi(\boldsymbol{r}, t) $ を外場無し固有状態で
\begin{align}
\psi(\boldsymbol{r}, t) = \sum\limits_{n, l, m, s_z} a_{nlms_z}(t)\, \varphi_{nlms_z}
\end{align}
のように展開して、展開係数が時間に依存すると考えることができるね。次に、$\hat{H} = \hat{H}_0 + \hat{V}(t)$ とおいてこれをシュレディンガー方程式に代入すると
\begin{align}
\sum\limits_{n, l, m, s_z}i\hbar\frac{d a_{nlms_z}(t)}{d t} \, \varphi_{nlms_z} = \sum\limits_{n, l, m, s_z}\left[E_n + \hat{V}(t)\right] a_{nlms_z}(t)\, \varphi_{nlms_z}
\end{align}
となるね。両辺に $\varphi_{n’l’m’s_z’}^*$ を掛けて全空間で積分すると展開係数に関する連立常微分方程式が得られるね。
\begin{align}
i\hbar\frac{d a_{n’l’m’s_z’}(t)}{d t} = E_{n’}a_{n’l’m’s_z’}(t) + \sum\limits_{n, l, m, s_z} a_{nlms_z}(t) \int \varphi_{n’l’m’s_z’}^* \hat{V}(t)\varphi_{nlms_z} dV
\end{align}
この $\hat{V}(t)$ に電磁波との相互作用を与えるわけだね。$\hat{\boldsymbol{p}}/m_e = -i [\hat{H}_0,\boldsymbol{r} ]/\hbar$ を考慮して、$\hat{V}(t)$ の空間積分の項を見てみよう。
\begin{align}
\int \varphi_{n’l’m’s_z’}^* \hat{V}(t)\varphi_{nlms_z} dV &\ = \int \varphi_{n’l’m’s_z’}^* \left[
-i\frac{e}{\hbar} [\hat{H}_0,\boldsymbol{r} ]\cdot\boldsymbol{A} + \frac{e }{m_e} \hat{S}_yB_y + \frac{e^2 A_0^2}{2m_e}\, \cos^2(kx-\omega t) \right] \varphi_{nlms_z} dV \\
&\ = \int \varphi_{n’l’m’s_z’}^* \left[
-ie \frac{ E_{n’} – E_n }{\hbar}\, z A_0 \cos(kx-\omega t) + \frac{ek\hbar A_0 s_z}{m_e} \,\sin(kx-\omega t) + \frac{e^2 A_0^2}{2m_e}\, \cos^2(kx-\omega t) \right] \varphi_{nlms_z} dV \\
&\ = -\frac{i A_0e}{2} e^{-i\omega t}\int \varphi_{n’l’m’s_z’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z + \frac{k\hbar s_z}{m_e} \right] e^{ikx} \varphi_{nlms_z} dV\\
&\ \ \ \ \ -\frac{i A_0e}{2} e^{i\omega t}\int \varphi_{n’l’m’s_z’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z – \frac{ k\hbar s_z}{m_e} \right] e^{-ikx} \varphi_{nlms_z} dV\\
&\ \ \ \ \ + \frac{e^2 A_0^2}{8m_e} \left[ 1 + e^{-2i\omega t} \int \varphi_{n’l’m’s_z’}^* e^{2ikx} \varphi_{nlms_z} dV + e^{2i\omega t} \int \varphi_{n’l’m’s_z’}^* e^{-2ikx} \varphi_{nlms_z} dV \right]
\end{align}
最後の変形は時間依存部分を積分の外に出すために、
\begin{align}
\cos(kx-\omega t) &\ = \frac{1}{2} \left[ e^{ikx-i\omega t} + e^{-ikx+i\omega t} \right]\\
\sin(kx-\omega t) &\ = \frac{1}{2i} \left[ e^{ikx-i\omega t} – e^{-ikx+i\omega t} \right]\\
\end{align}
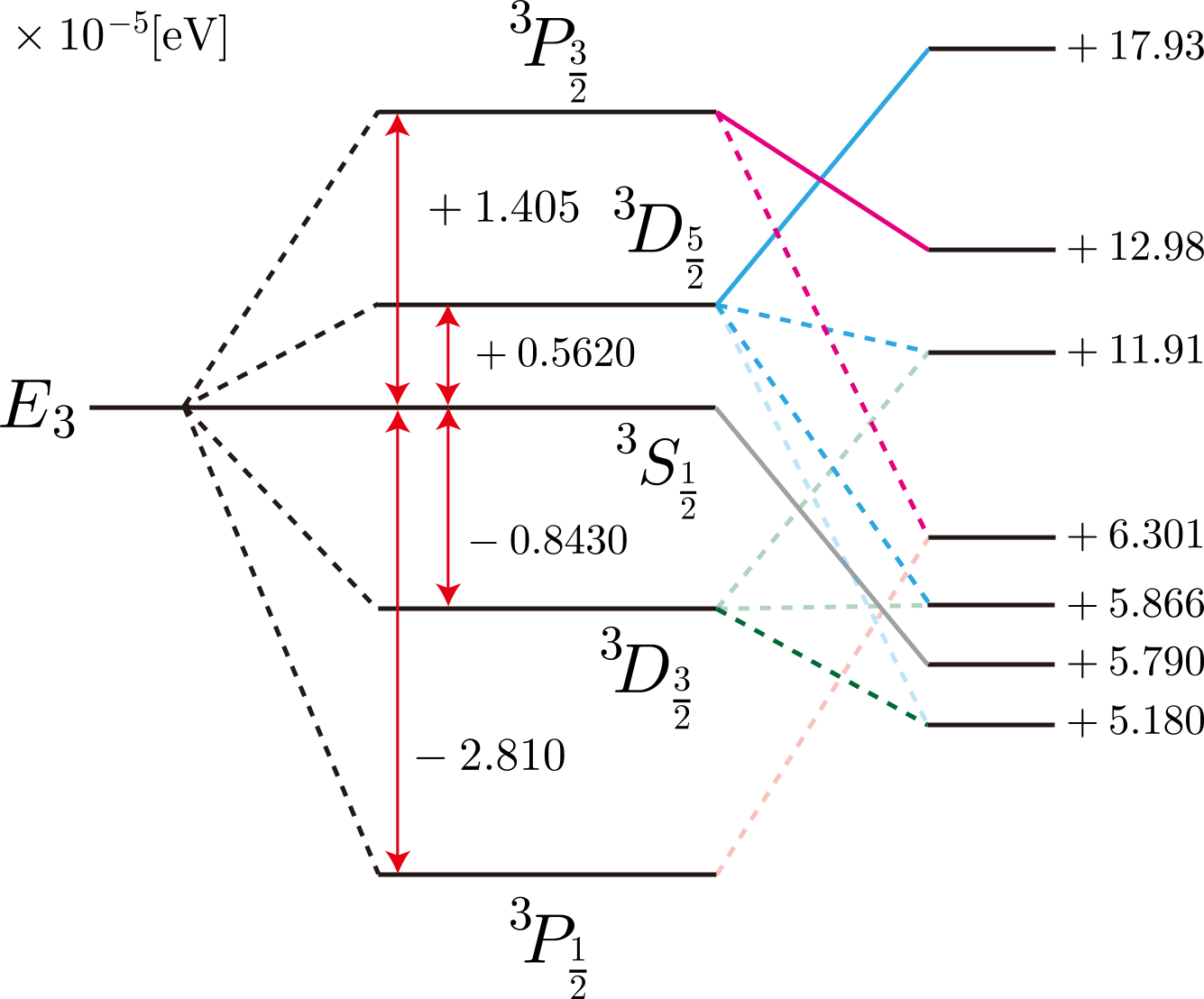
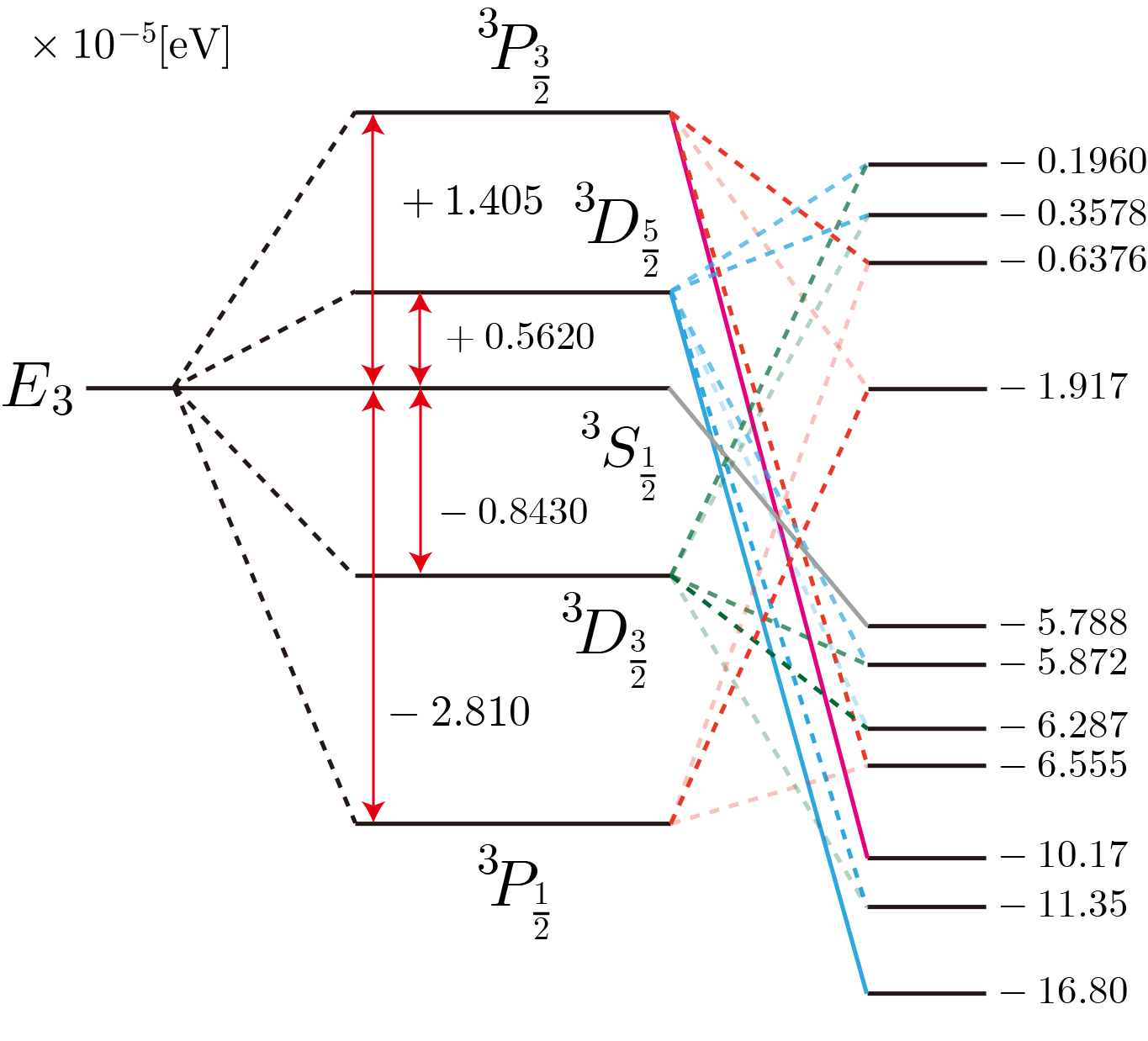
と変形しているよ。ちょっと複雑になったけれども、時間依存部分はすべて積分の外に出たので、時間ステップごとに積分を実行しなくて済むね。あとは、ルンゲ・クッタ法などの常微分方程式を解く計算アルゴリズムで、この連立常微分方程式が得られるね。ちなみに、$\hat{\boldsymbol{p}}\cdot\boldsymbol{A}$ は電子の軌道運動による電磁波の吸収と放出を、$\hat{\boldsymbol{s}}\cdot\boldsymbol{B}$ は電子のスピンによる電磁波の吸収と放出を表すよ。また、$\boldsymbol{A}^2$ は電磁場の量子化後に分かるけれども、光子の2個吸収、2個放出、光子の散乱に寄与するよ。
スピンと2次の項を無視する場合
先のポテンシャル積分項にて、スピンと2次の効果を無視すると
\begin{align}
\int \varphi_{n’l’m’}^* \hat{V}(t)\varphi_{nlm} dV = -\frac{i A_0e}{2} \left[e^{-i\omega t}\int \varphi_{n’l’m’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z \right] e^{ikx} \varphi_{nlm} dV + e^{i\omega t}\int \varphi_{n’l’m’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z \right] e^{-ikx} \varphi_{nlm} dV \right]
\end{align}
となるね。さらに、原子サイズに対して、波の波長が十分に大きい場合、$ e^{ikx} \simeq 1 $、$ e^{-ikx} \simeq 1$ が十分成り立つね(光子のエネルギー $10[{\rm eV}]$ の波長が約 $100 [{\rm nm}]$ なので十分だね)。積分に関係ない部分をすべて外に出すと
\begin{align}
\int \varphi_{n’l’m’}^* \hat{V}(t)\varphi_{nlm} dV = -i A_0e \frac{ E_{n’} – E_n }{\hbar} \cos(\omega t) \int \varphi_{n’l’m’}^* z \varphi_{nlm} dV
\end{align}
となって、ポテンシャル積分項は、係数を除いて、実質的に以前解説した電気双極子の行列要素と一致するね。このハミルトニアンを元に、次回は水素原子の基底状態にいる電子に電磁波を与えてみるよ。