スピン1/2の粒子2個が存在する場合、それぞれのスピンの値によって、波動関数の空間部分は「対称」あるいは「反対称」となることが知られているね。今回は、最も簡単な1次元自由空間中で2個の粒子が平面波で表される場合の空間分布を復習するよ。波動関数の空間部分の対称関数と反対称関数はそれぞれ
\begin{align}
\psi^{(S)}(x_1, x_2, t) &\ = \frac{1}{\sqrt{2}} \left[ e^{i k_1\cdot x_1 +i k_2\cdot x_2} + e^{i k_1\cdot x_2 +i k_2\cdot x_1}\right]e^{-i\omega t} \\
\psi^{(A)}(x_1, x_2, t) &\ =\frac{1}{\sqrt{2}} \left[ e^{i k_1\cdot x_1 +i k_2\cdot x_2}- e^{i k_1\cdot x_2 +i k_2\cdot x_1}\right]e^{-i\omega t}\\
\end{align}
となるね。ただし、
\begin{align}
E_1 = \frac{\hbar^2 k_1^2}{2m_e} \ , \ E_2 = \frac{\hbar^2 k_2^2}{2m_e} \ , \ E = E_1 + E_2 \ , \ \omega = \frac{E}{\hbar}
\end{align}
の関係があるよ。この波動関数は、粒子1と粒子2のそれぞれの位置 $x_1$ と $x_2$ を与えたときの振幅を与えるので、1次元上で波動関数の様子を可視化するには工夫が必要になるね。今回は、粒子1の位置をゼロ、すなわち $x_1 =0$ として、横軸を粒子2の位置 $x_2$、縦軸を波動関数の実部、虚部、絶対値の2乗の値とするね。なお、波動関数の絶対値の2乗
\begin{align}
|\psi^{(S)}(x_1, x_2, t)|^2 &\ = 1 + \cos\left[ (k_1 – k_2)(x_1 – x_2) \right]\\
|\psi^{(A)}(x_1, x_2, t)|^2 &\ = 1 – \cos\left[ (k_1 – k_2)(x_1 – x_2) \right]\\
\end{align}
は、各点における粒子の存在確率(今回、規格化が不十分だったので最大値が2になってしまったよ)を表すよ。2粒子の場合には相対位置のみ依存しているね。
計算結果
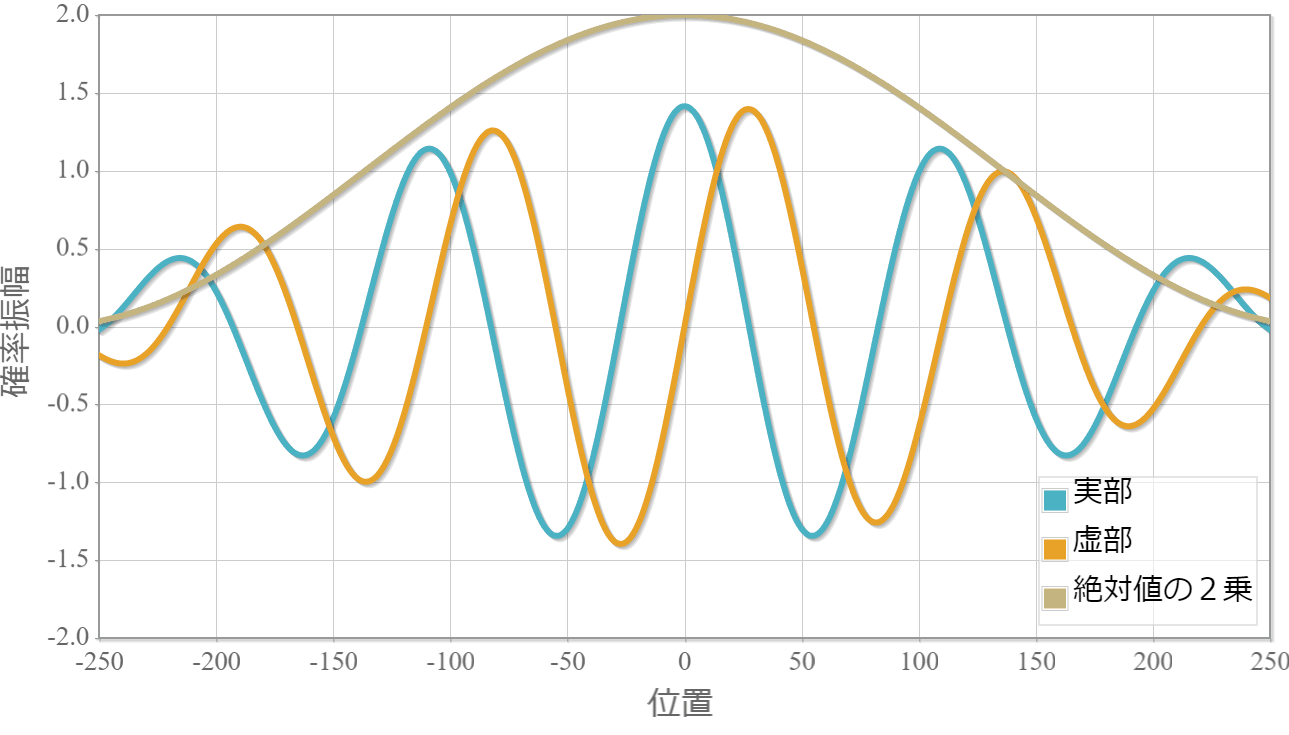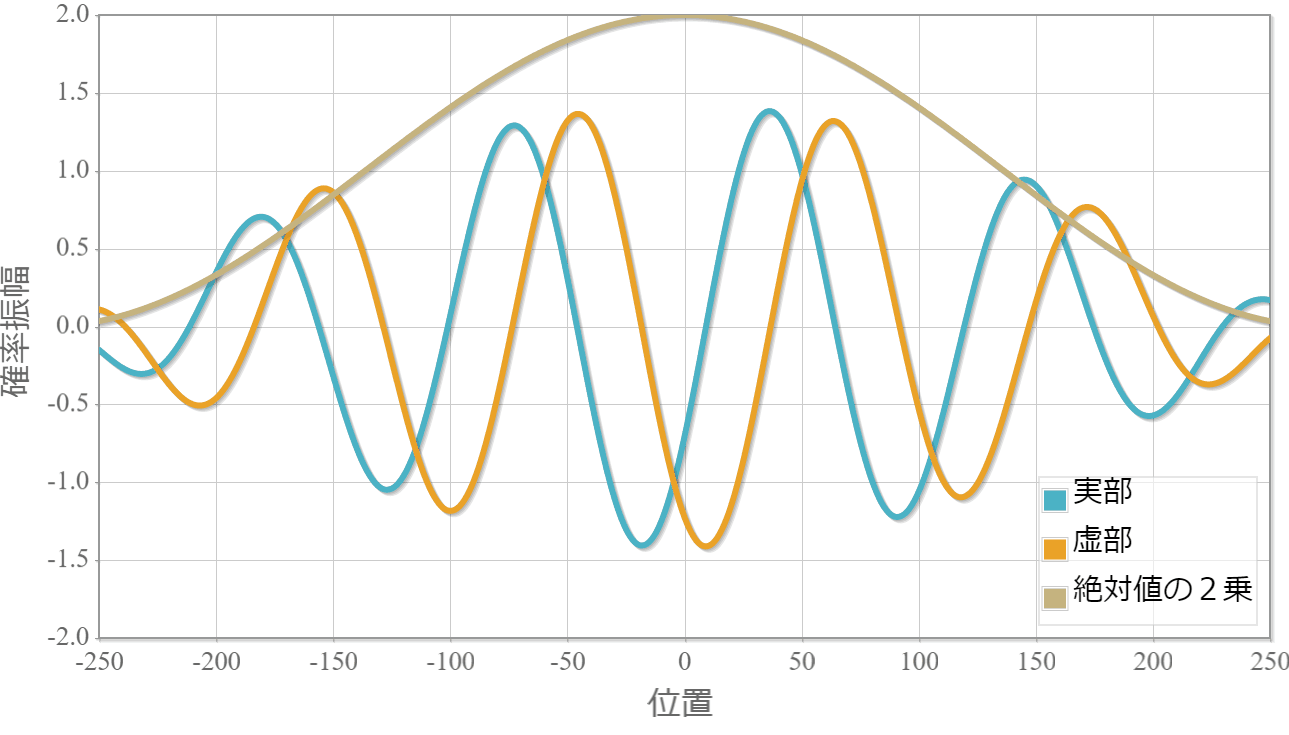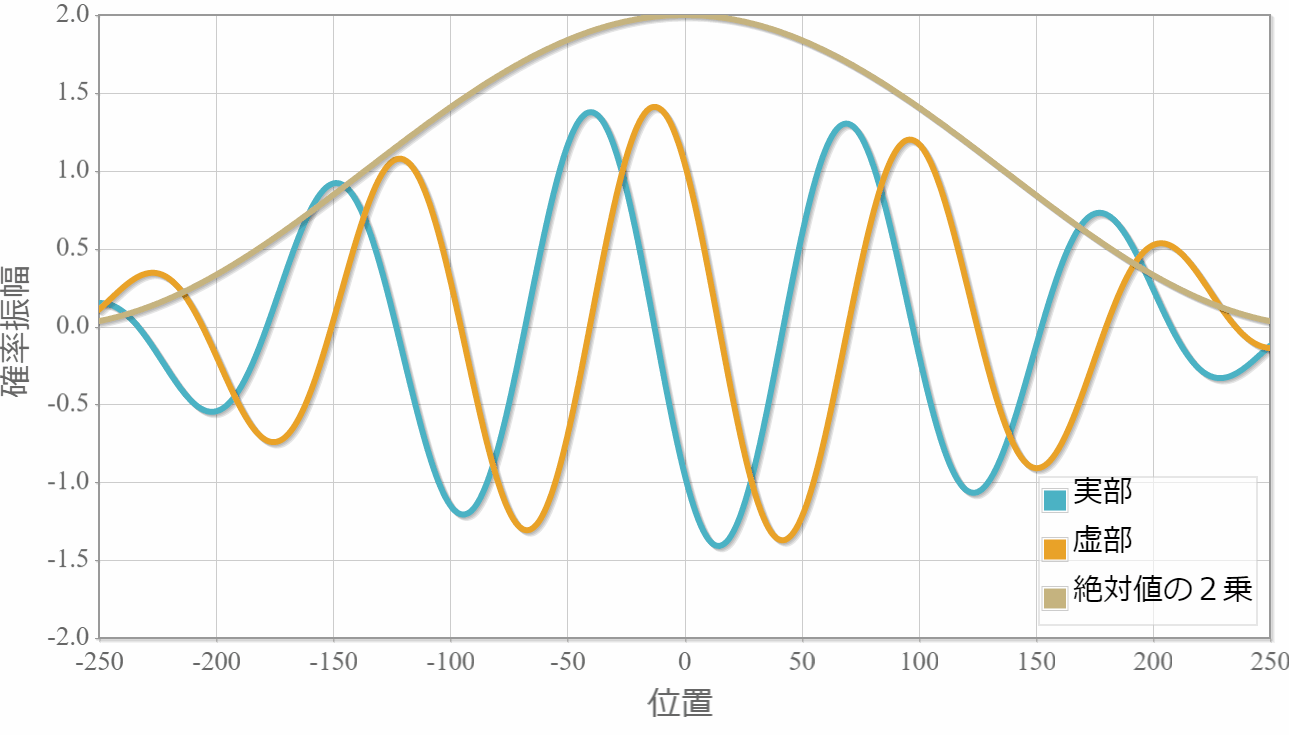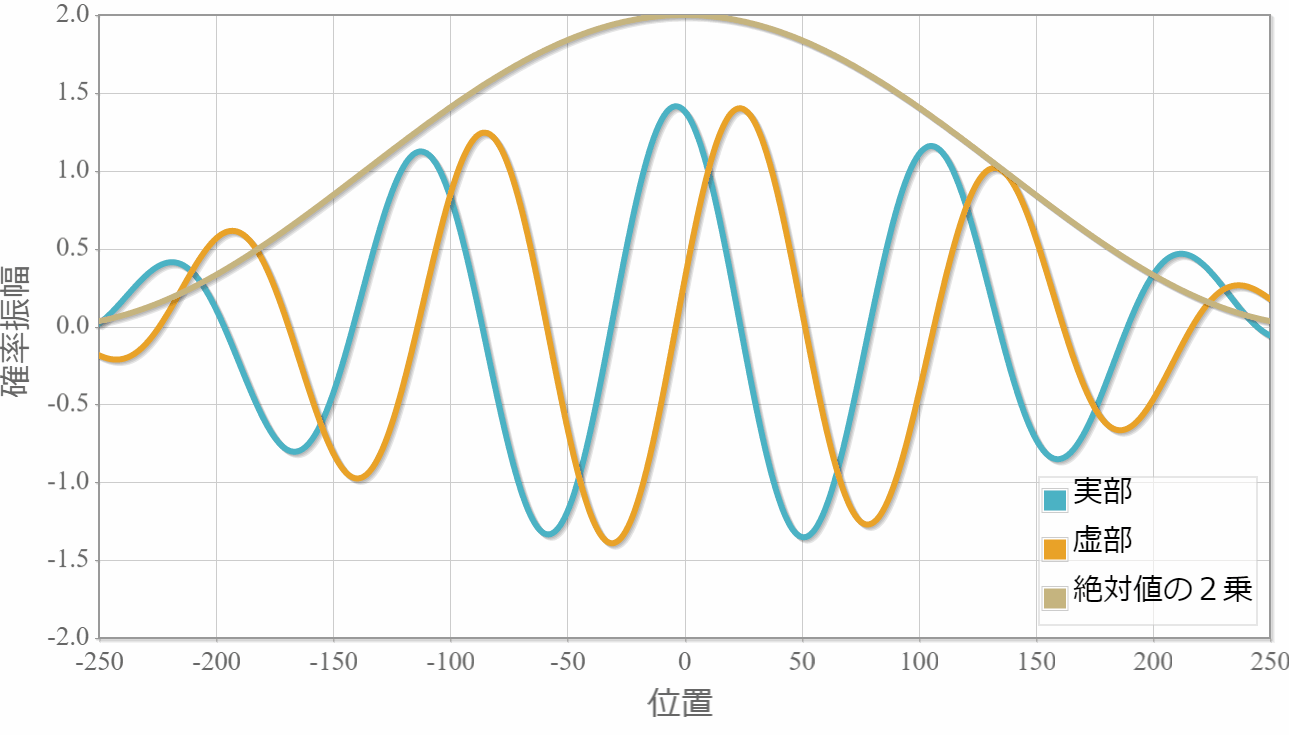
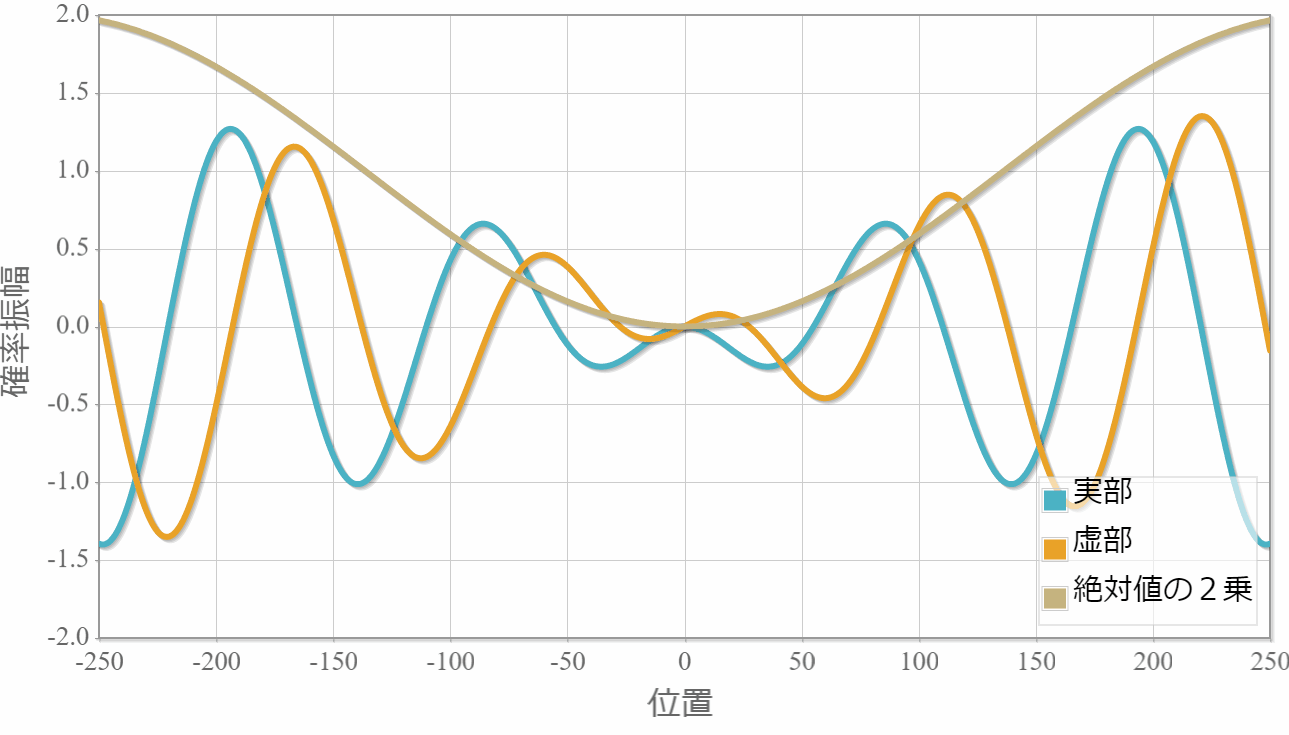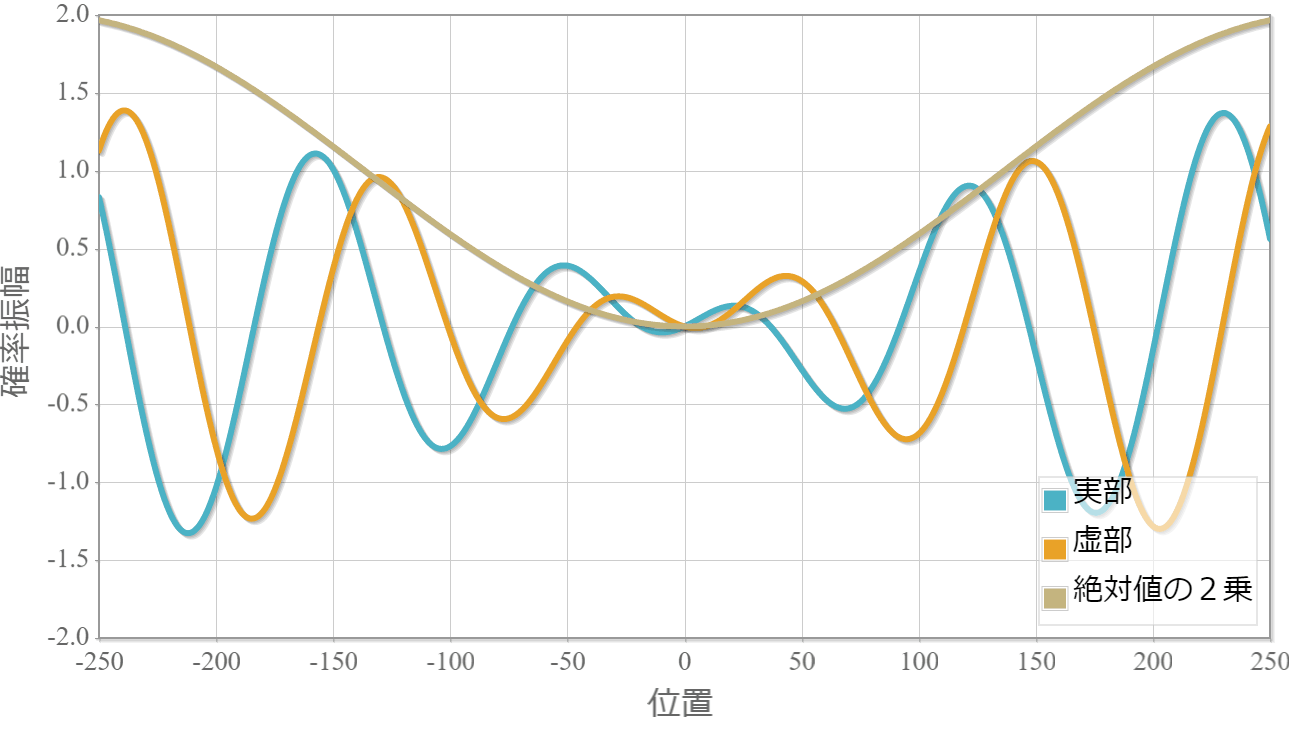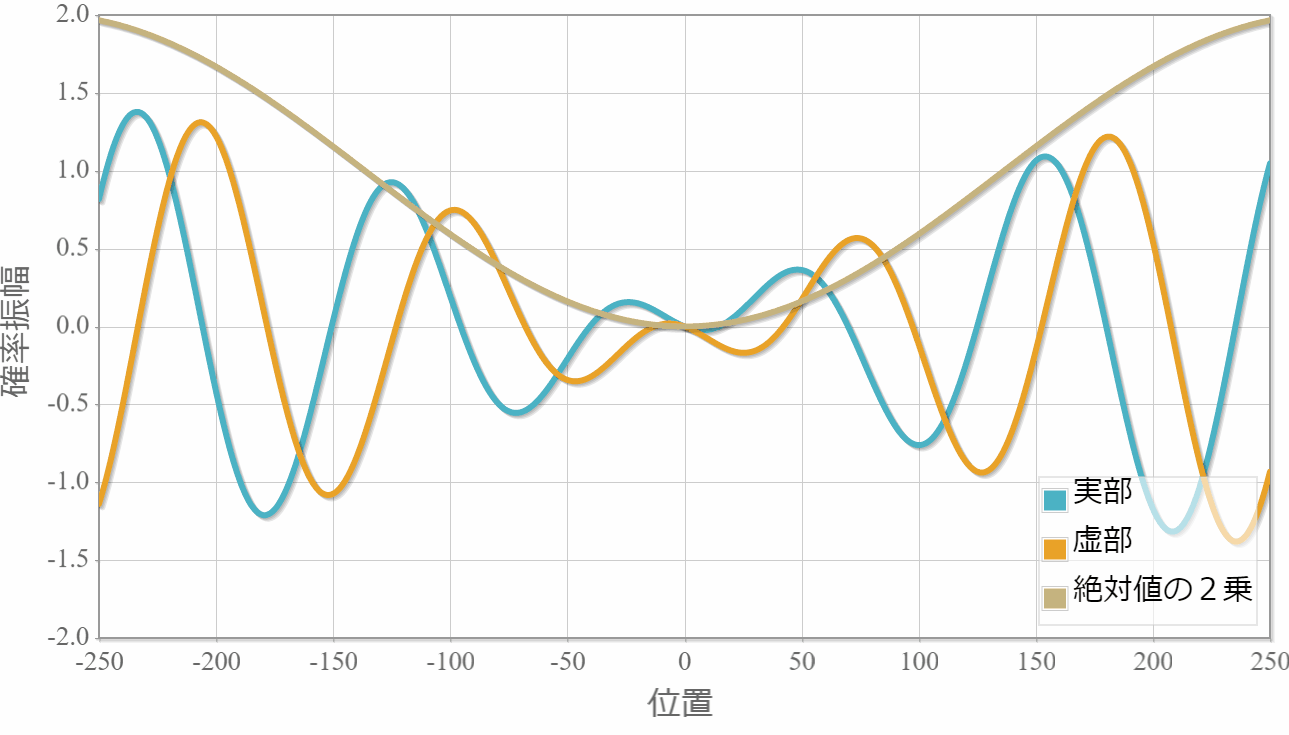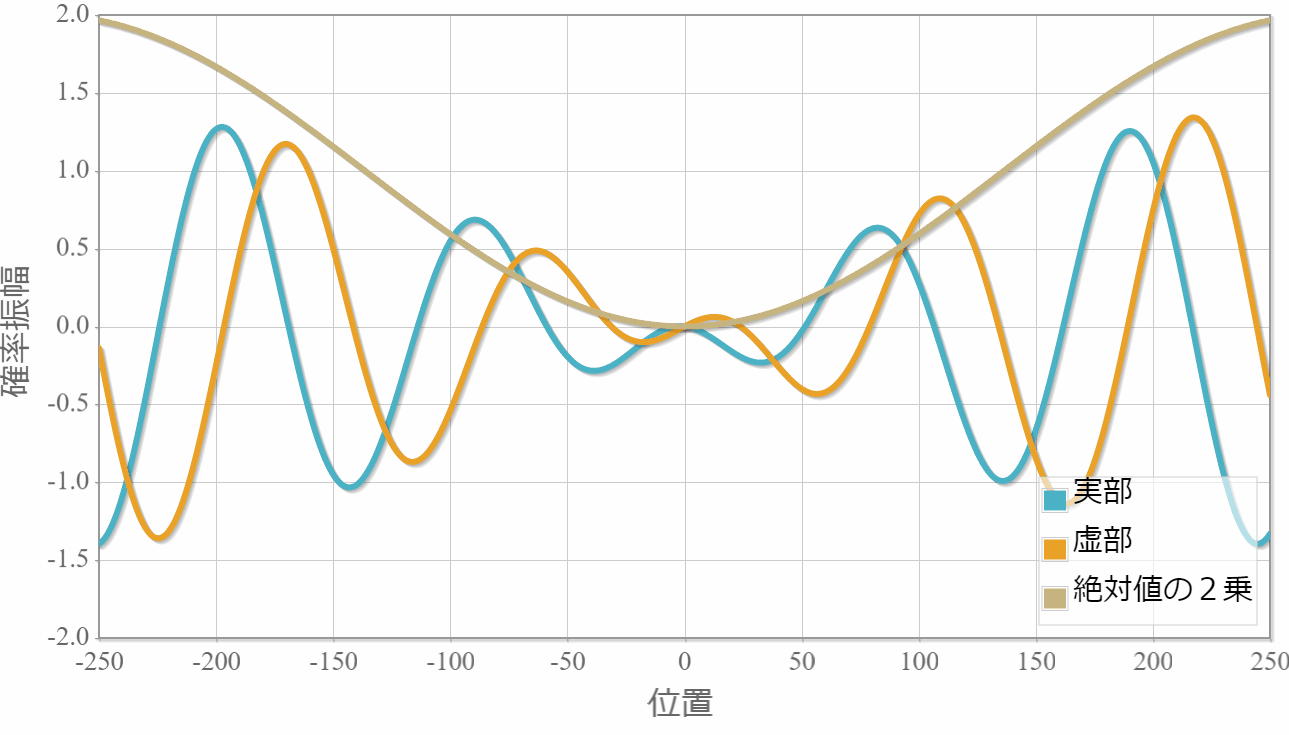
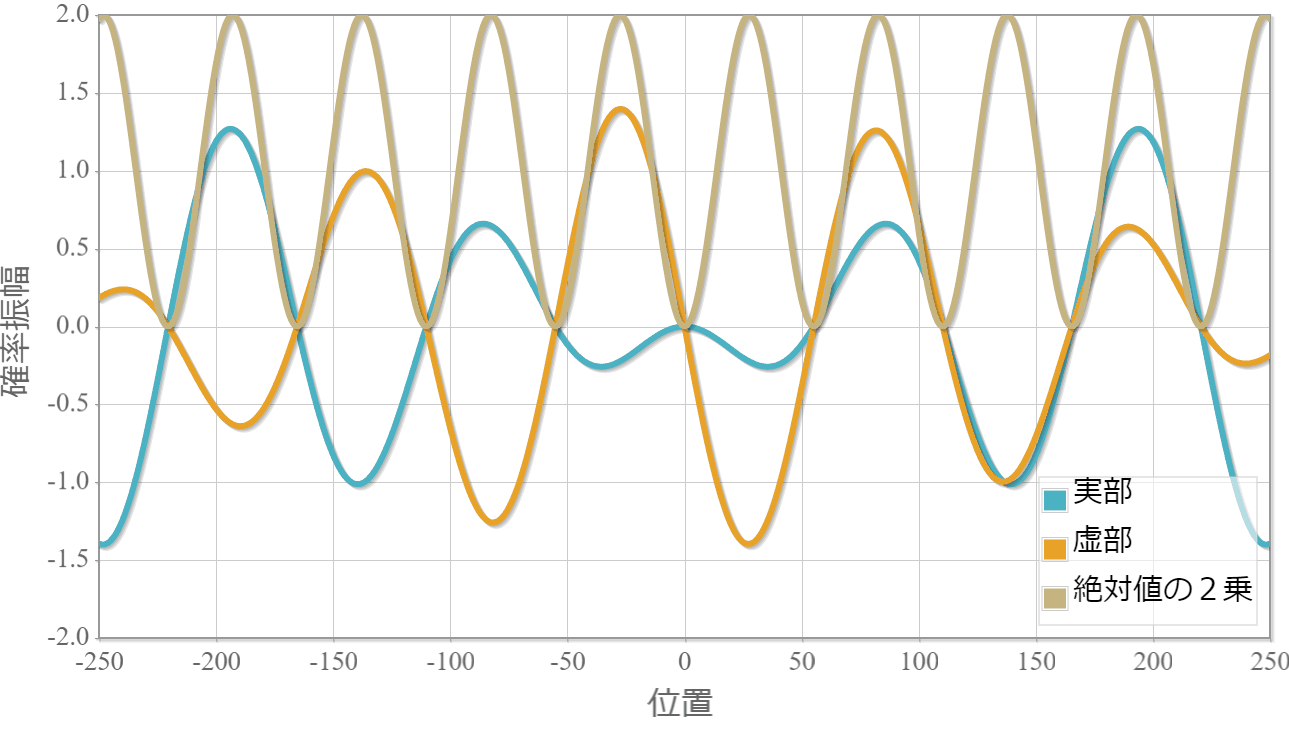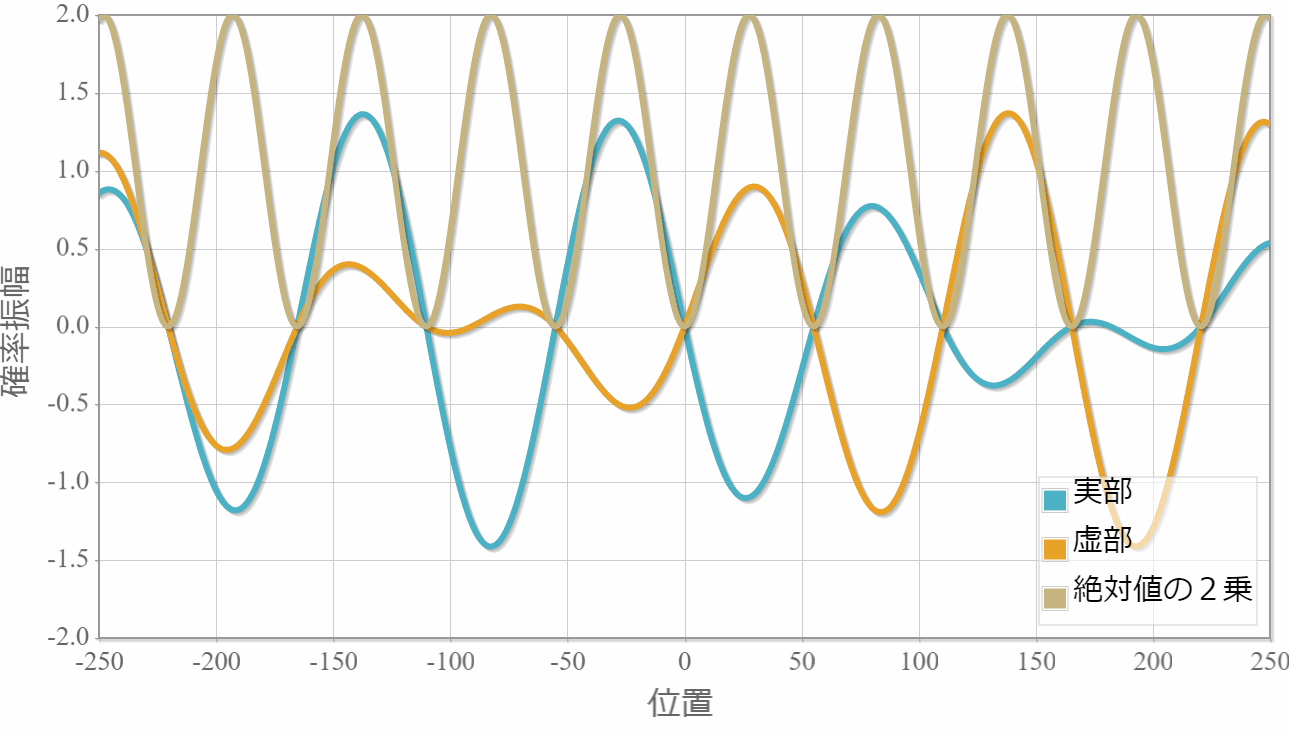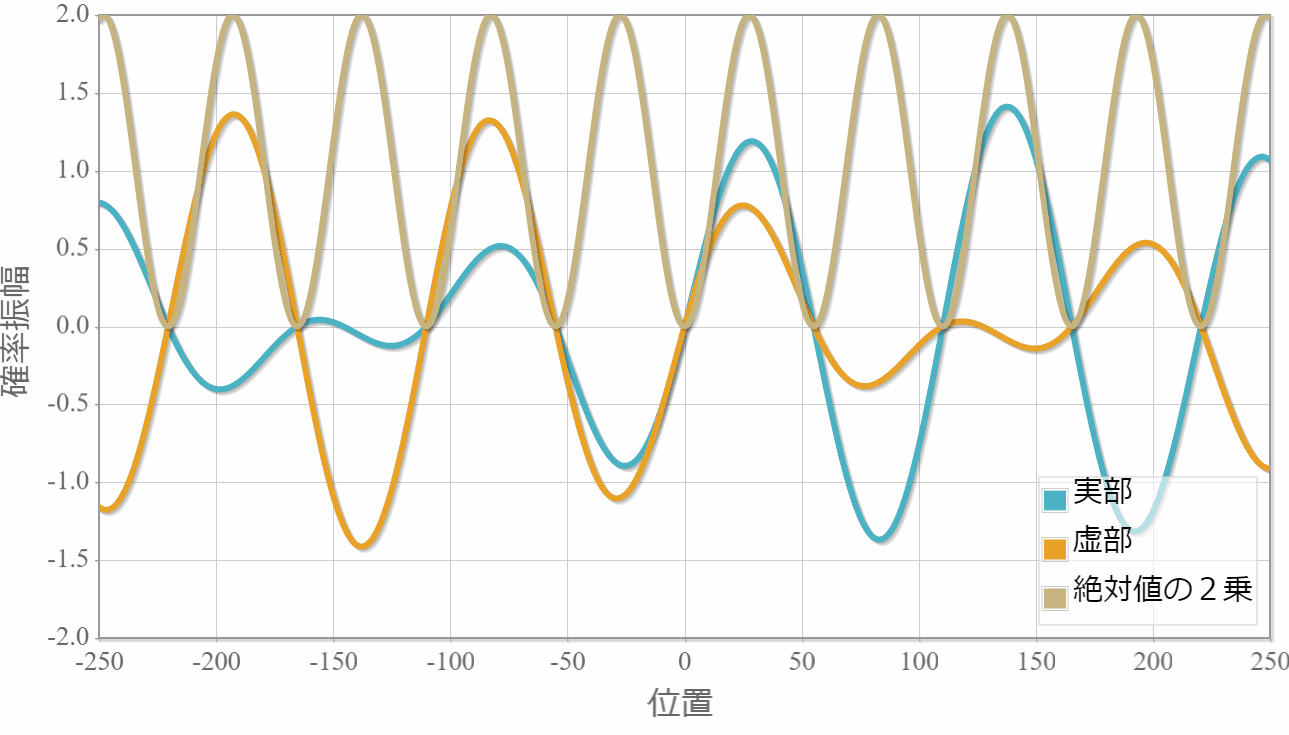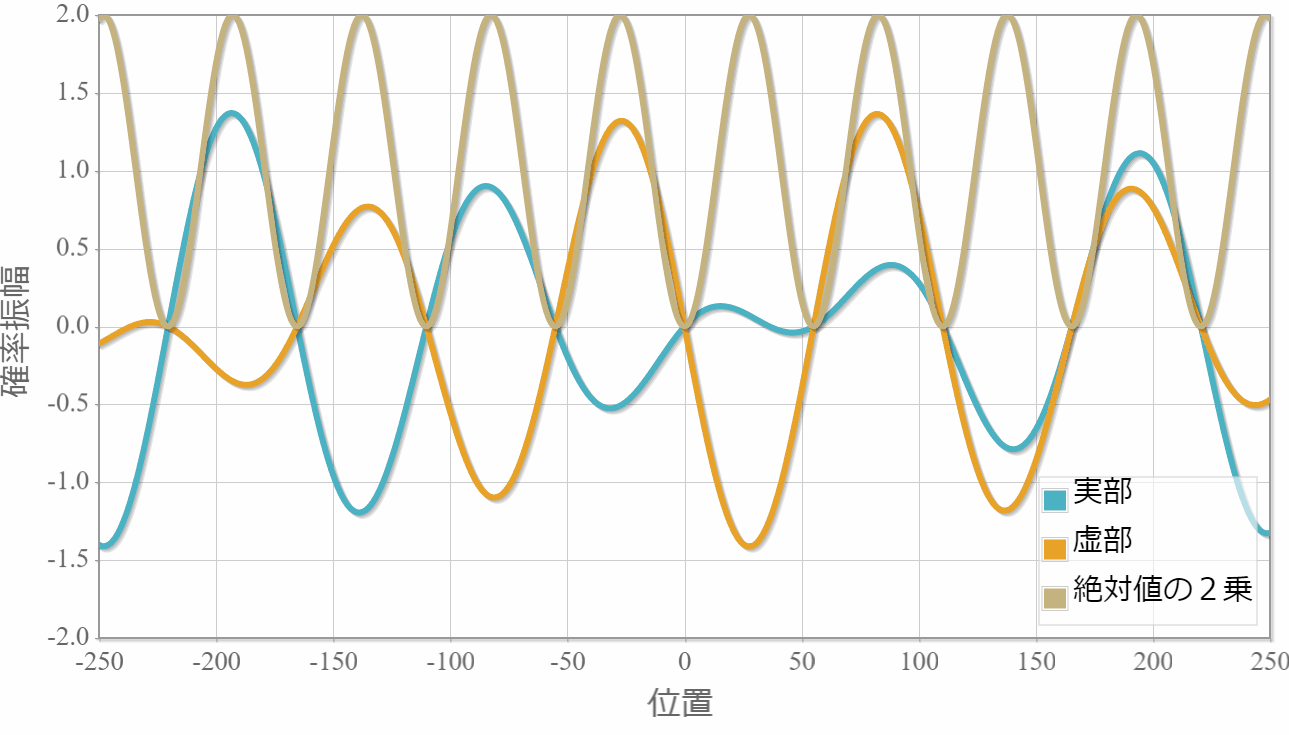
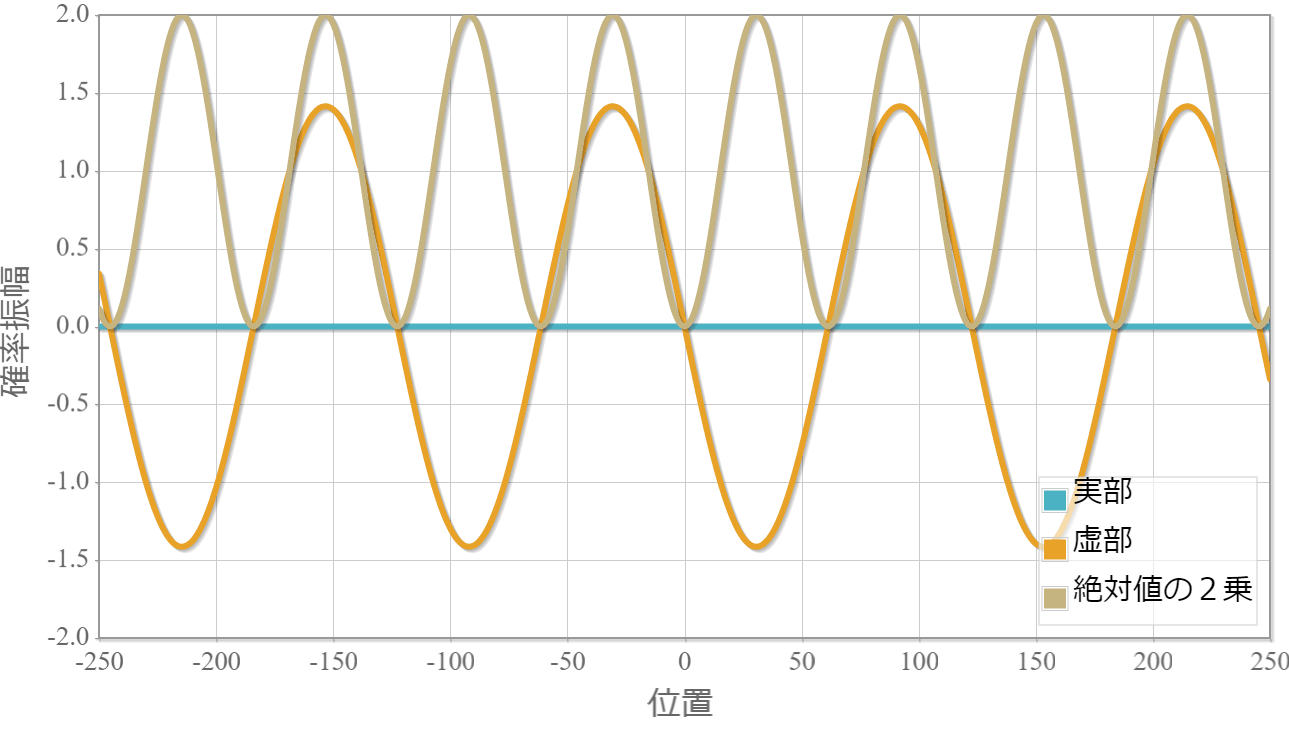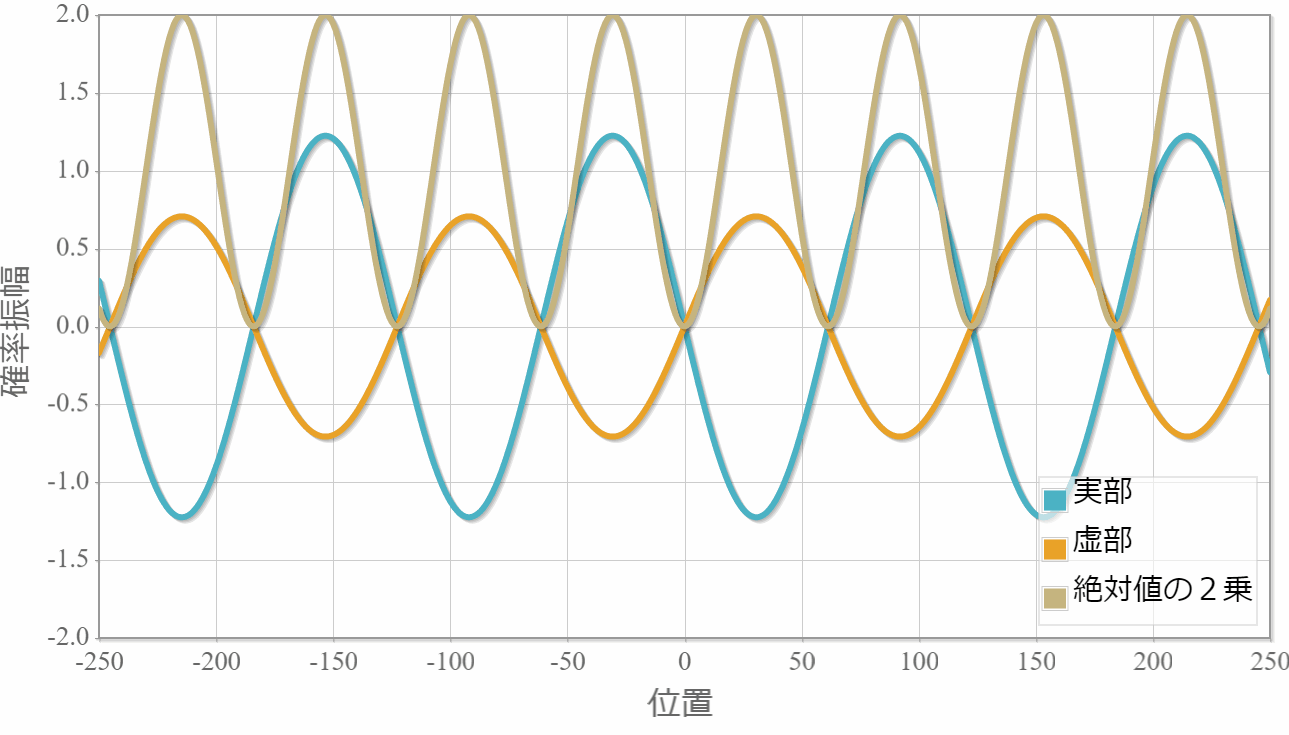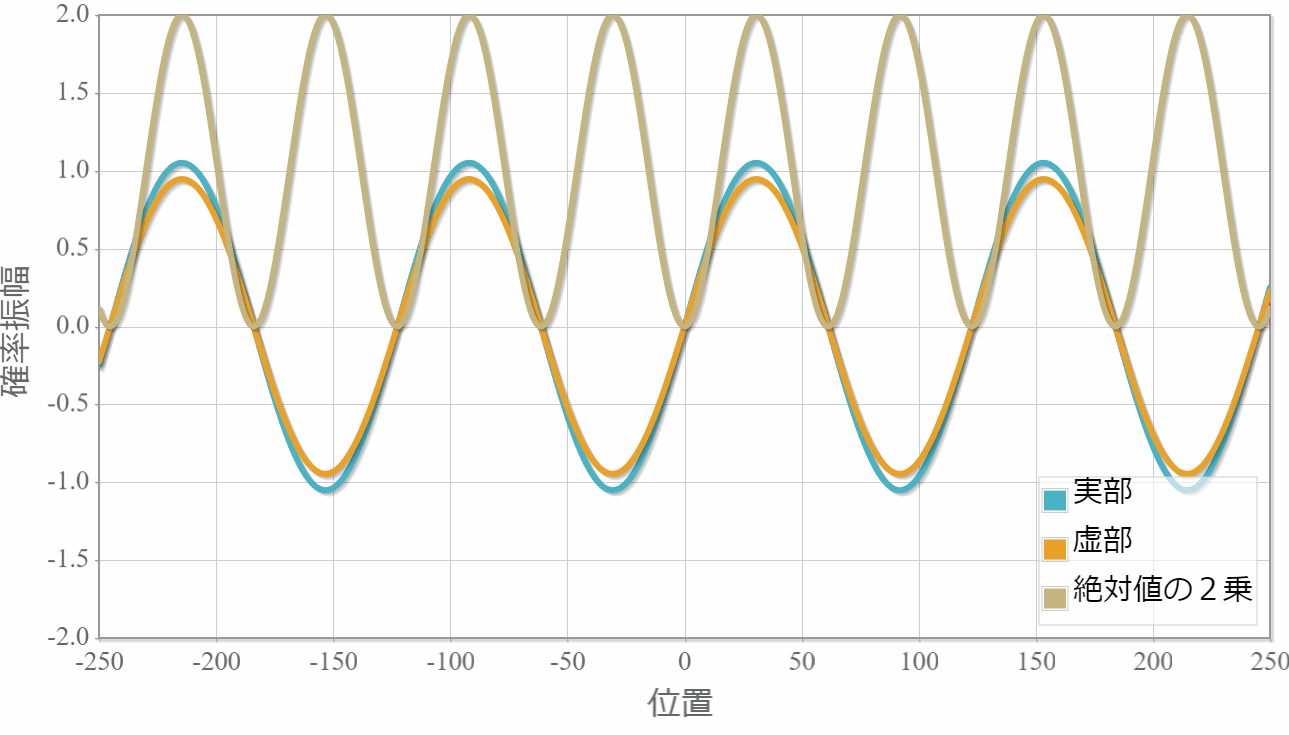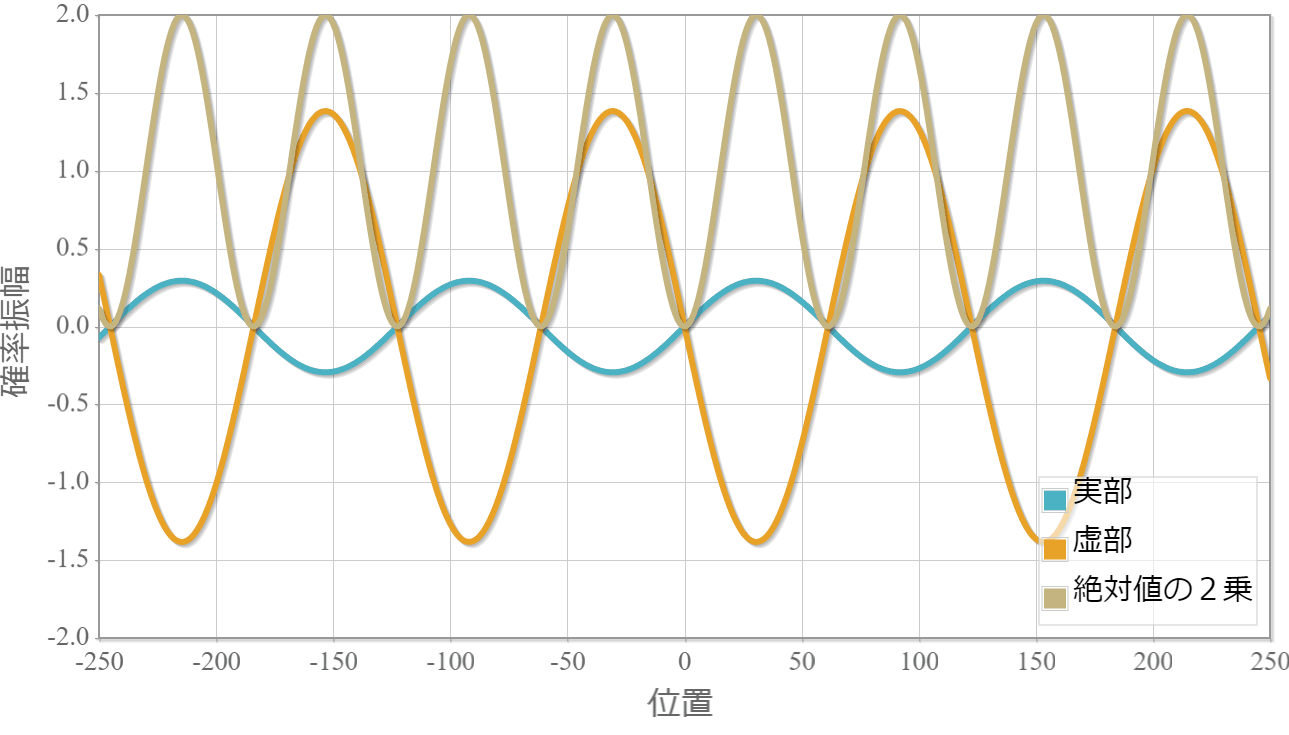
$E_1=1.0[{\rm eV}]$(右向き)と $E_2=1.5[{\rm eV}]$(右向き)
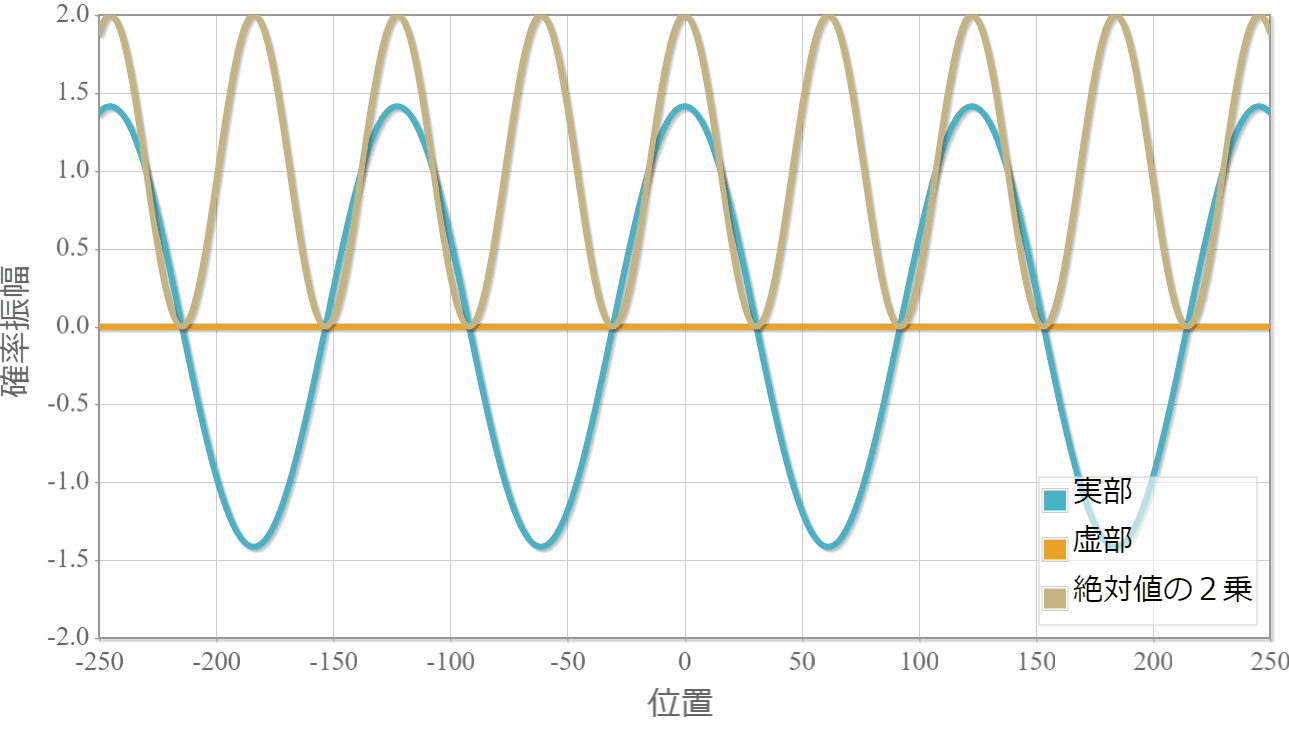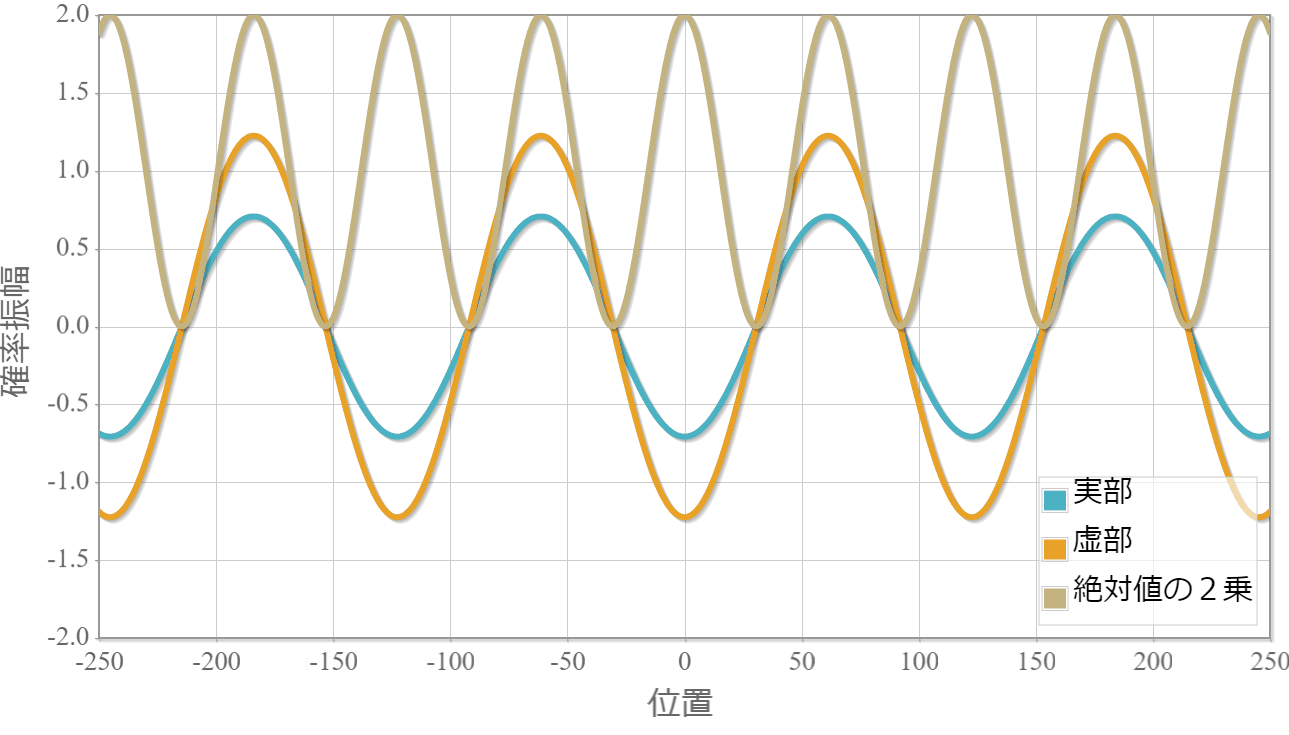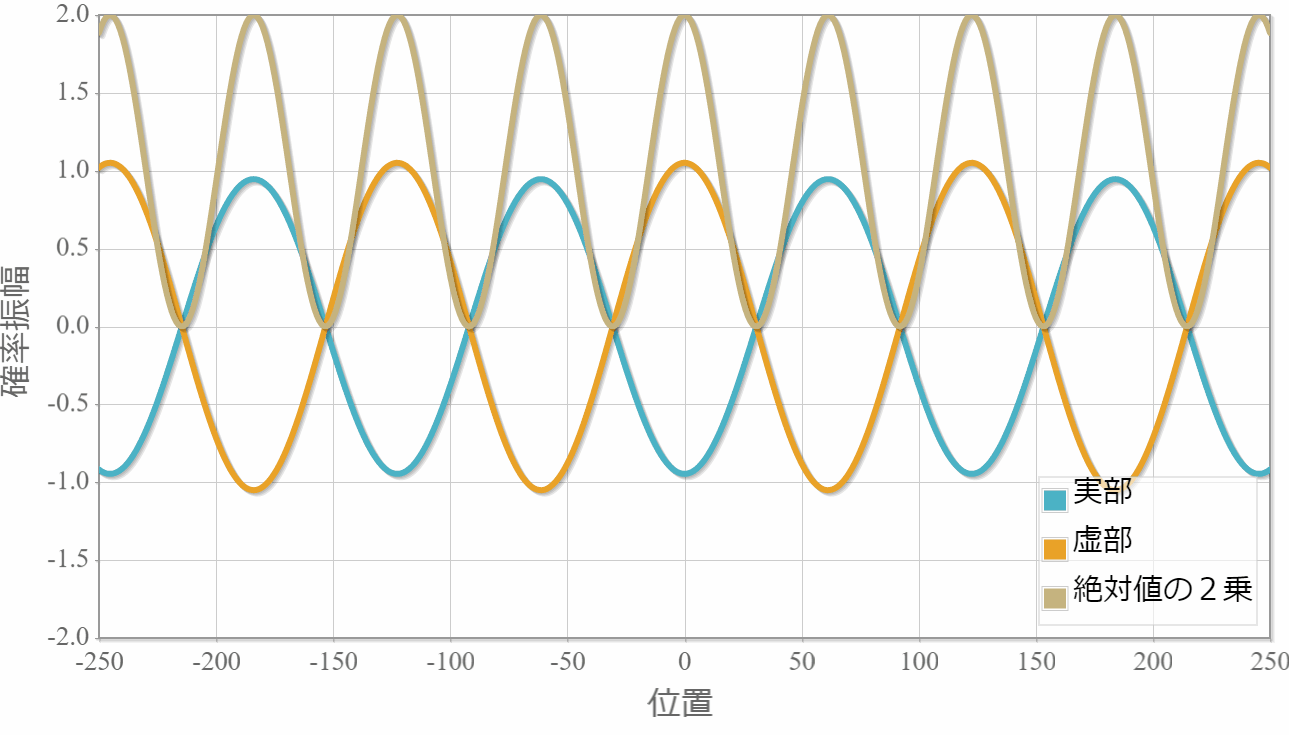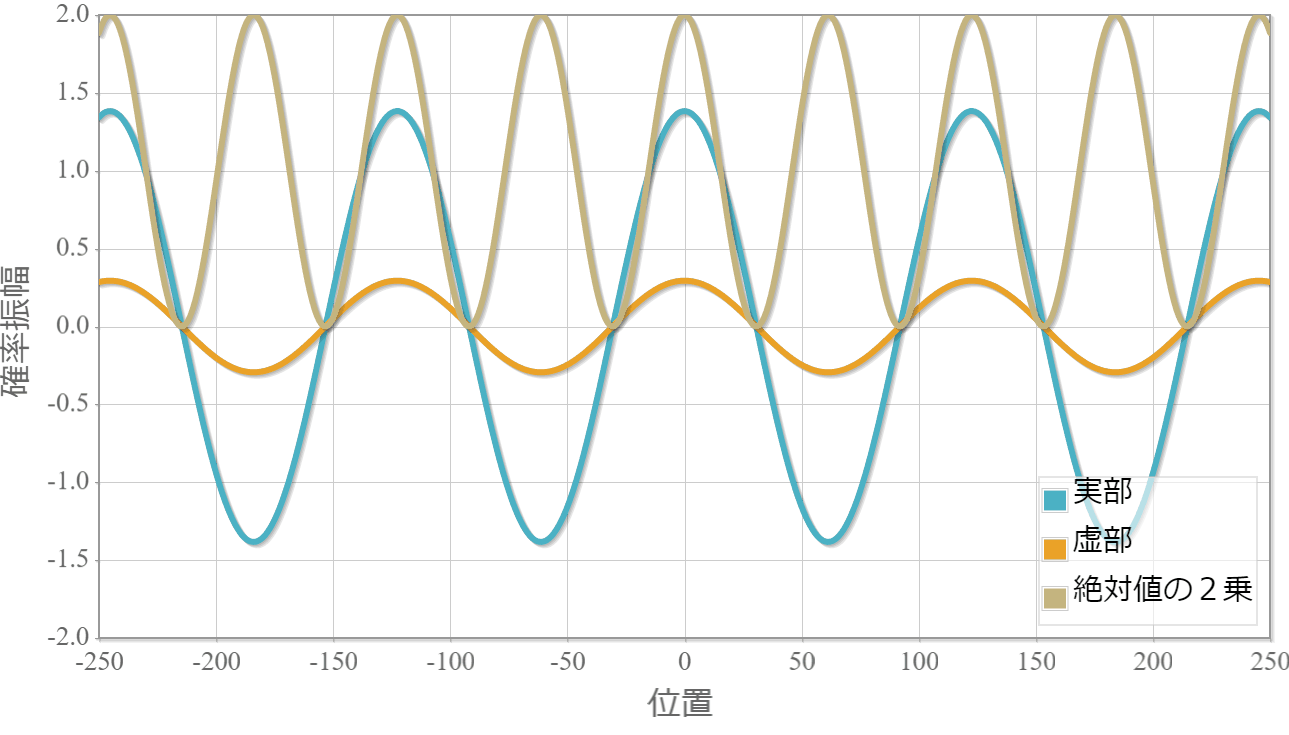
まずは、同じ方向へ進む2粒子の場合の計算結果を示すよ。粒子1の位置を $x_1 =0$ としているよ。対称関数の場合には粒子2はゼロ近傍にいる確率が高い反面、反対称波動関数の粒子2はゼロ近傍が一番低くなっているね。
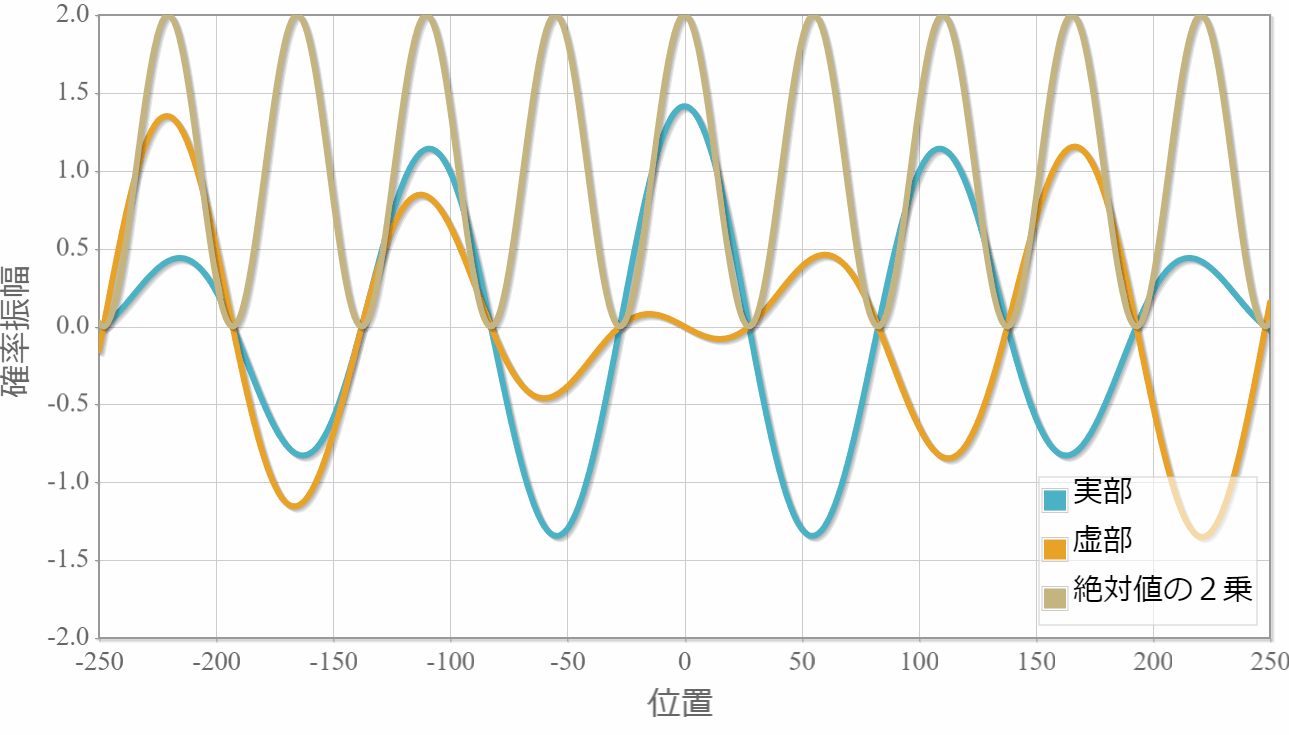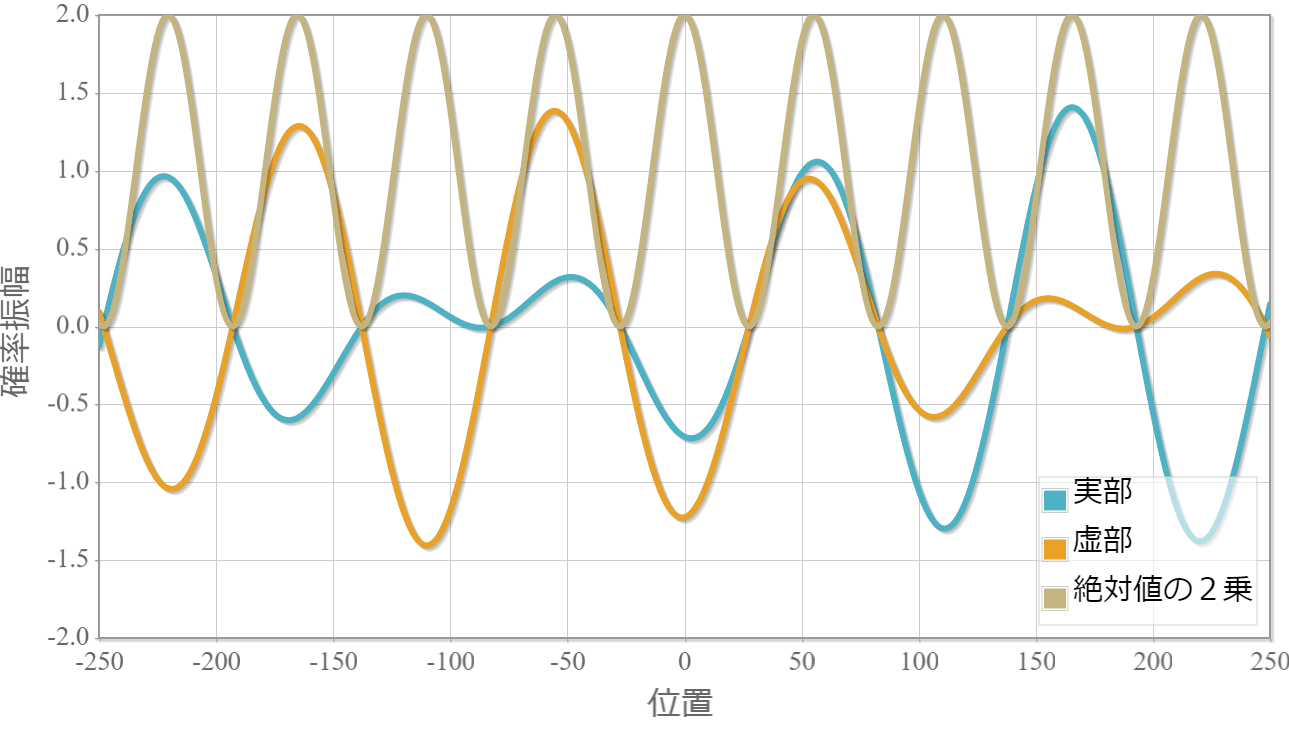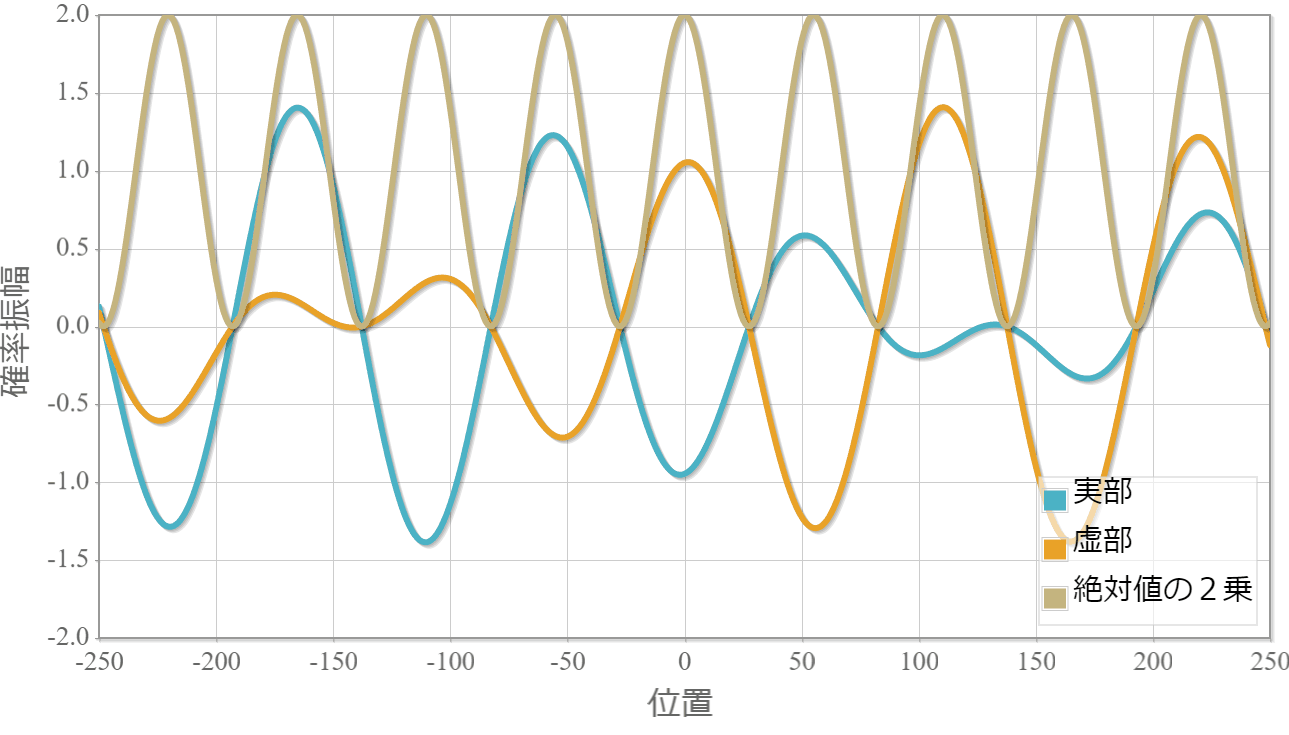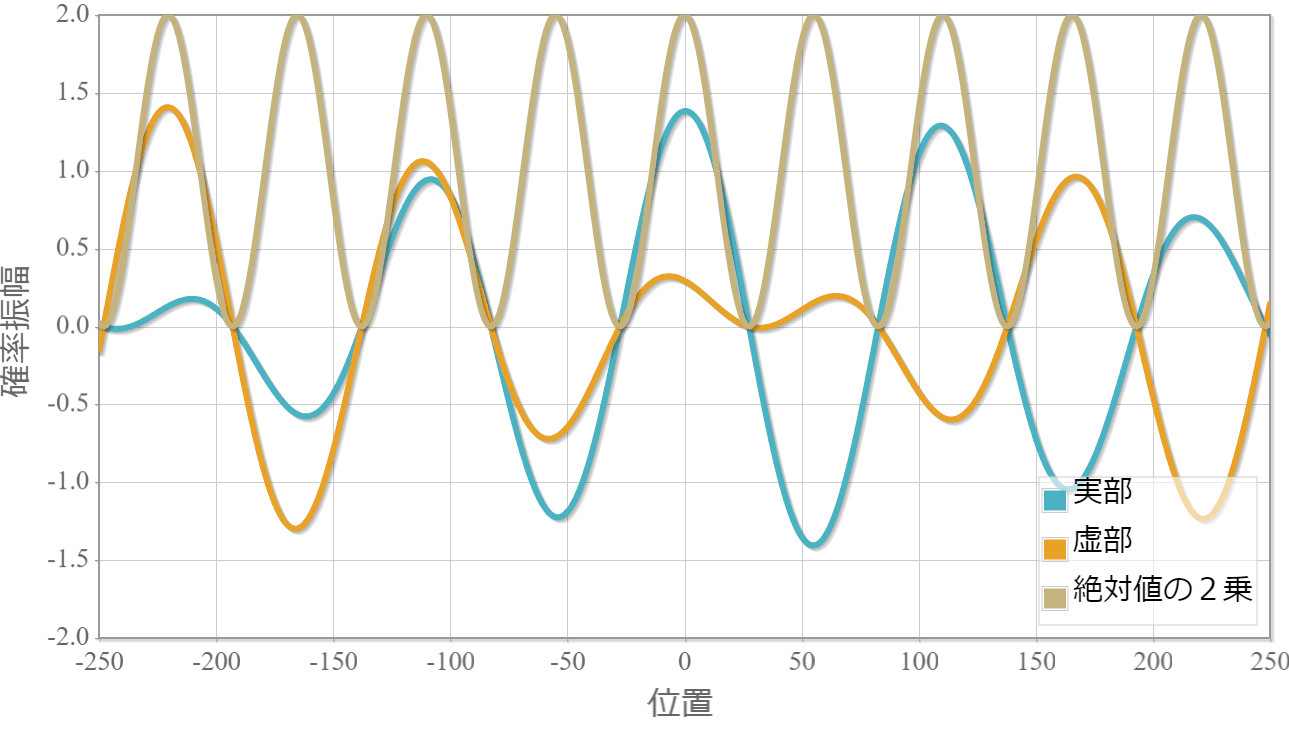
対称関数
反対称関数
$E_1=1.0[{\rm eV}]$(右向き)と $E_2=1.5[{\rm eV}]$(左向き)
次は、反対方向へ進む2粒子の場合の計算結果を示すよ。粒子1の位置を $x_1 =0$ としているよ。異なるエネルギー(波数)の干渉なのに、粒子2の存在確率が時間に依存しないのは、ちょっと不思議だけれども、先に示した絶対値の2乗の表式は時間に依存しないから当たり前だよね。あと、絶対値の2乗の波数が大きくなったね。これは、波数 $k_1$ と $k_2$ の差が存在確率の波数に対応していることで理解できるね。
対称関数
反対称関数
$E_1=1.0[{\rm eV}]$(右向き)と $E_2=1.0[{\rm eV}]$(左向き)
最後に、同じエネルギーの2粒子が反対方向へ進む場合の計算結果を示すよ。粒子1の位置を $x_1 =0$ としているよ。
対称関数
反対称関数
粒子が1個の場合は単純な平面波だけれども、2個になった途端に複雑さが増していくね。
