x軸方向に進む光はベクトルポテンシャル $\boldsymbol{A}$ で表すことができるね。
\begin{align}
\boldsymbol{A}= \left\{ \matrix{ 0 \cr A_{y0} \cos(kx-\omega t + \phi_y) \cr A_{z0} \cos(kx-\omega t + \phi_z) } \right.
\end{align}
この表式から、電場と磁場は次のように表されるね。
\begin{align}
\boldsymbol{E} = -\frac{\partial \boldsymbol{A}}{\partial t} = \left\{ \matrix{ 0 \cr-\omega A_{y0} \sin(kx-\omega t + \phi_y) \cr -\omega A_{z0} \sin(kx-\omega t + \phi_z) } \right.
\end{align}
\begin{align}
\boldsymbol{B} = \nabla\times \boldsymbol{A} = \left\{ \matrix{ 0 \cr k A_{z0} \sin(kx-\omega t +
\phi_z) \cr -k A_{y0} \sin(kx-\omega t + \phi_y) } \right.
\end{align}
直線偏光( $A_{y0} = A_{z0}$ かつ $\phi_z = \phi_y $ )
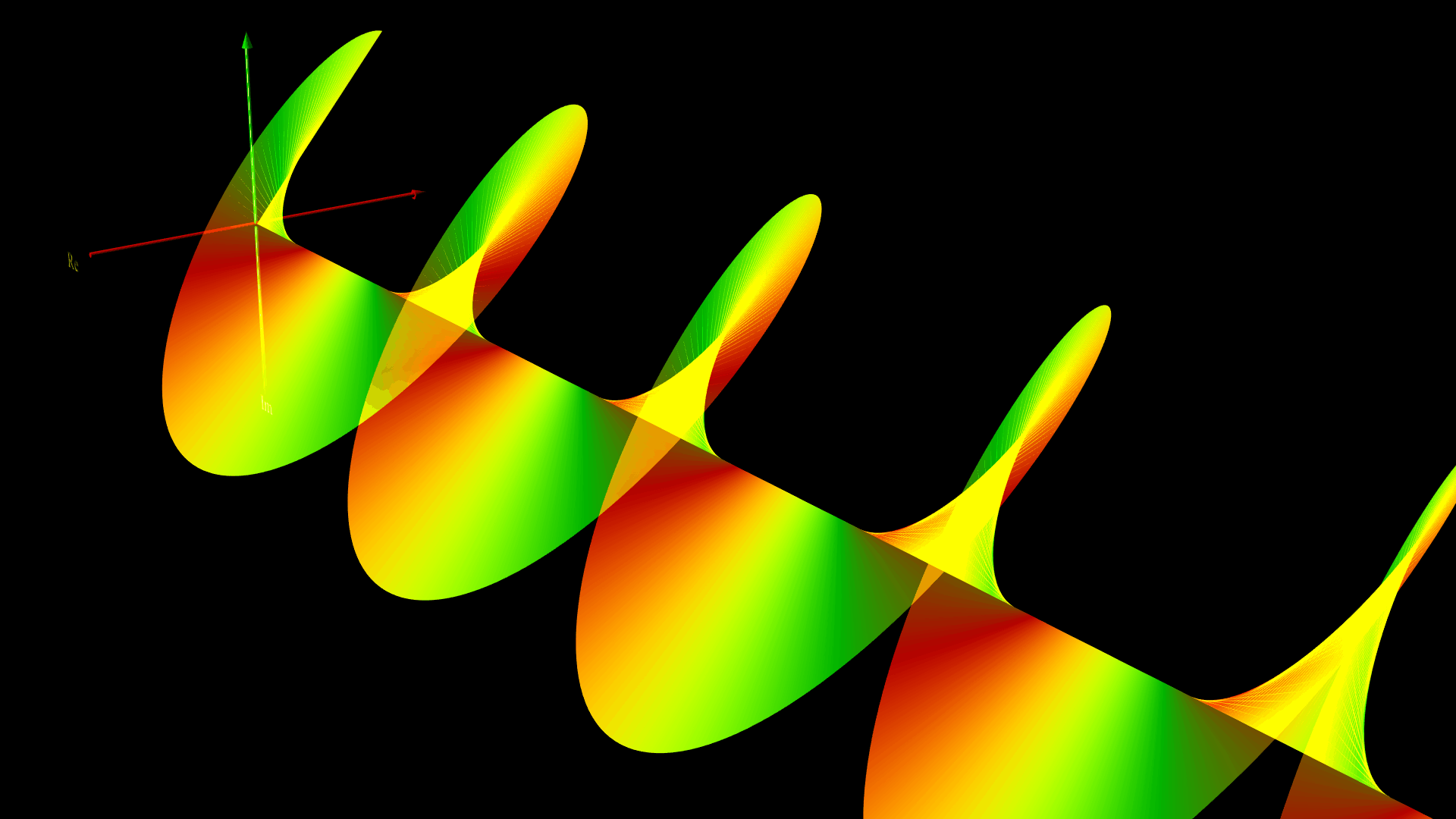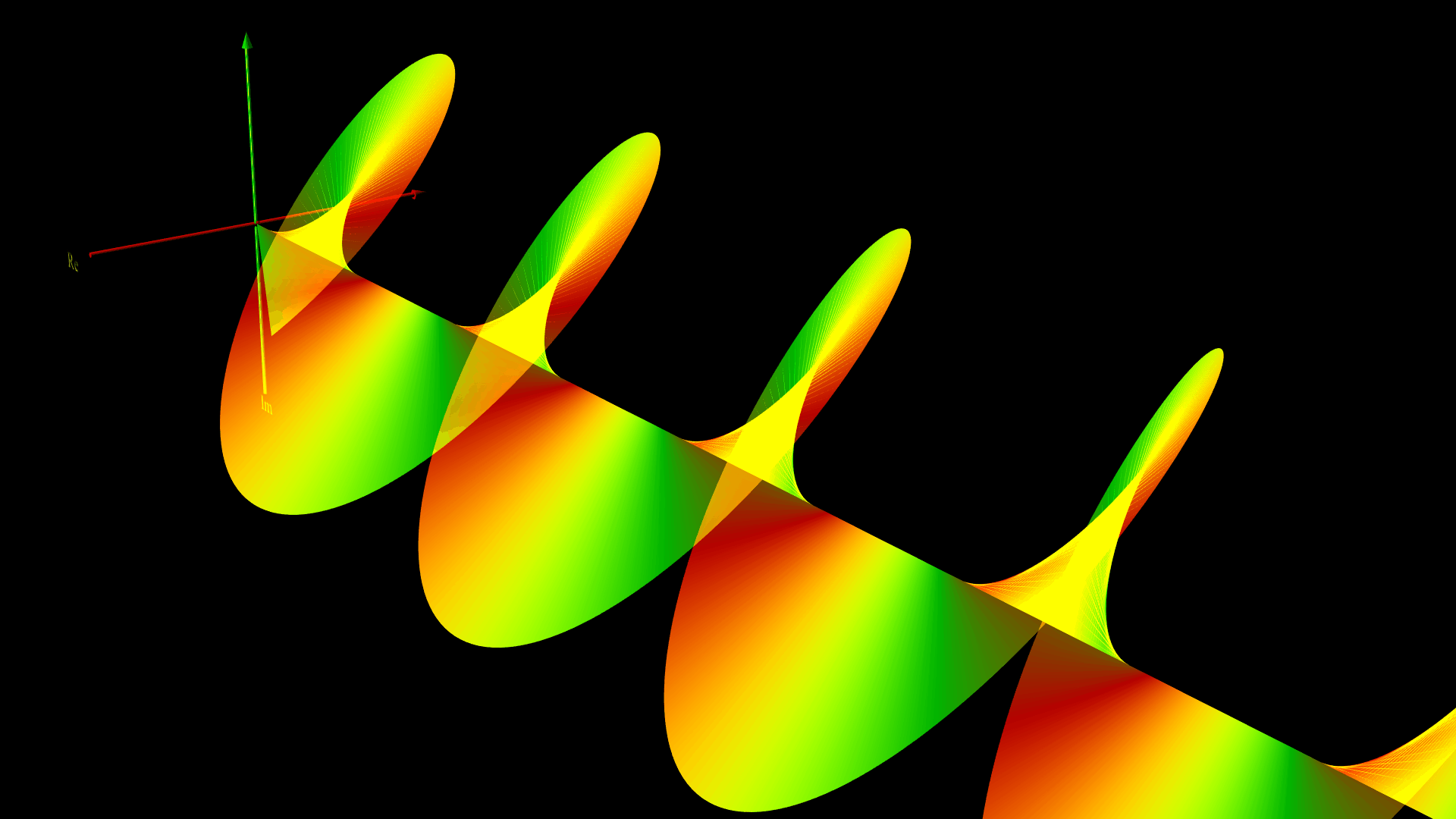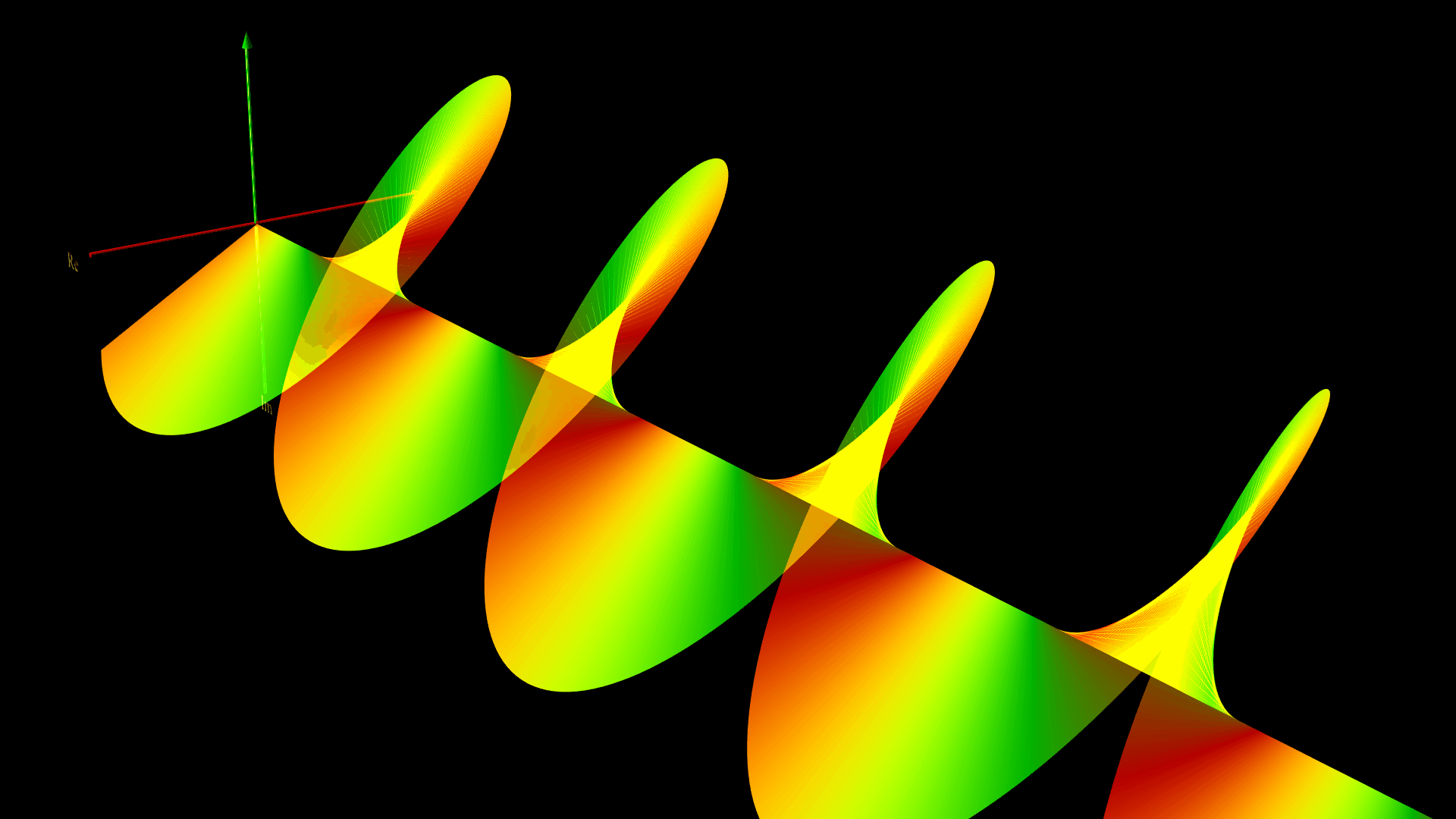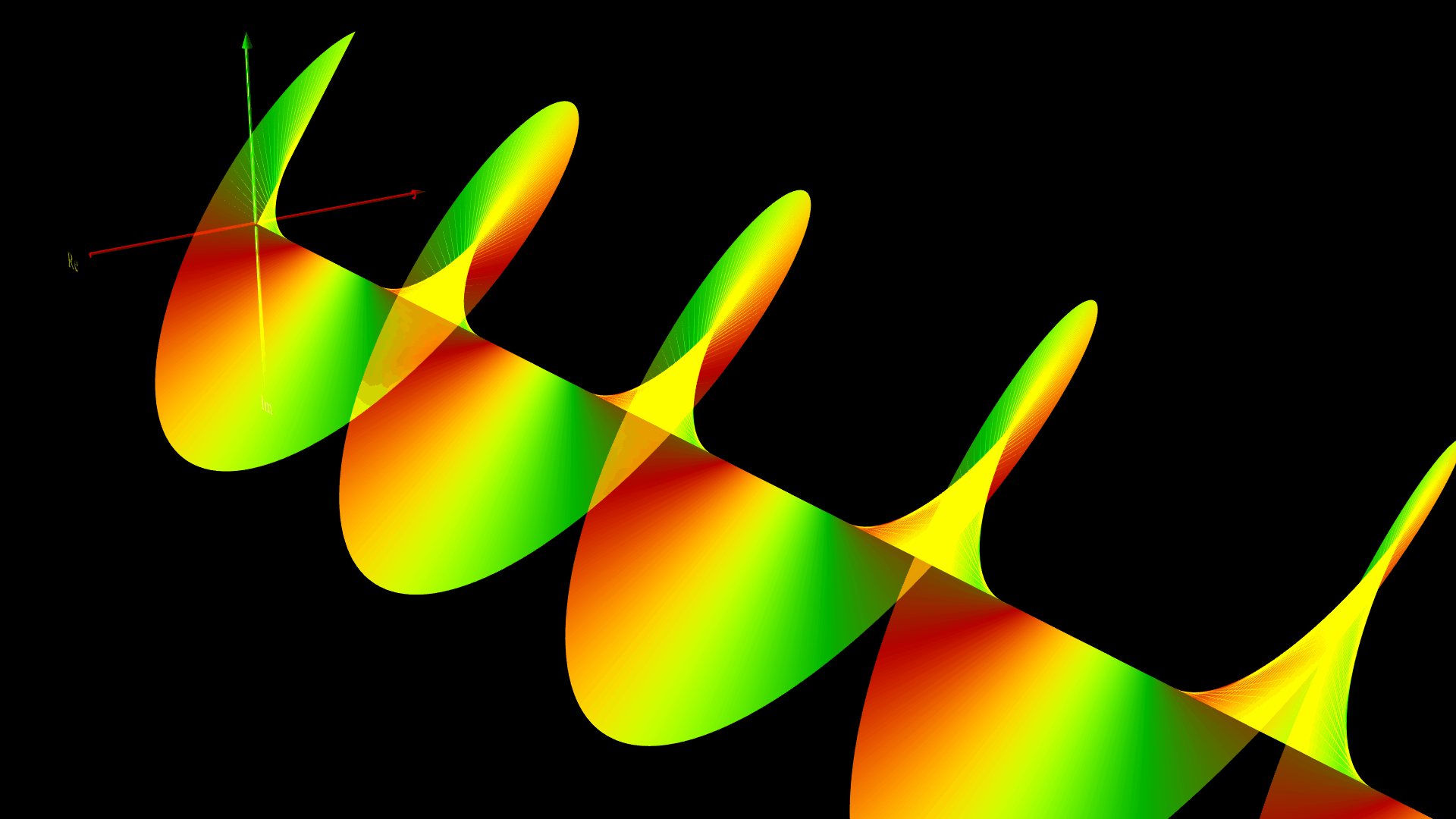
下の図は、$ A_{y0} =1 , \ A_{z0} = 1$ 、$\phi_z = \phi_y = 0$ として、電場の向きを水平にとったときの電場と磁場のグラフィックスだよ。
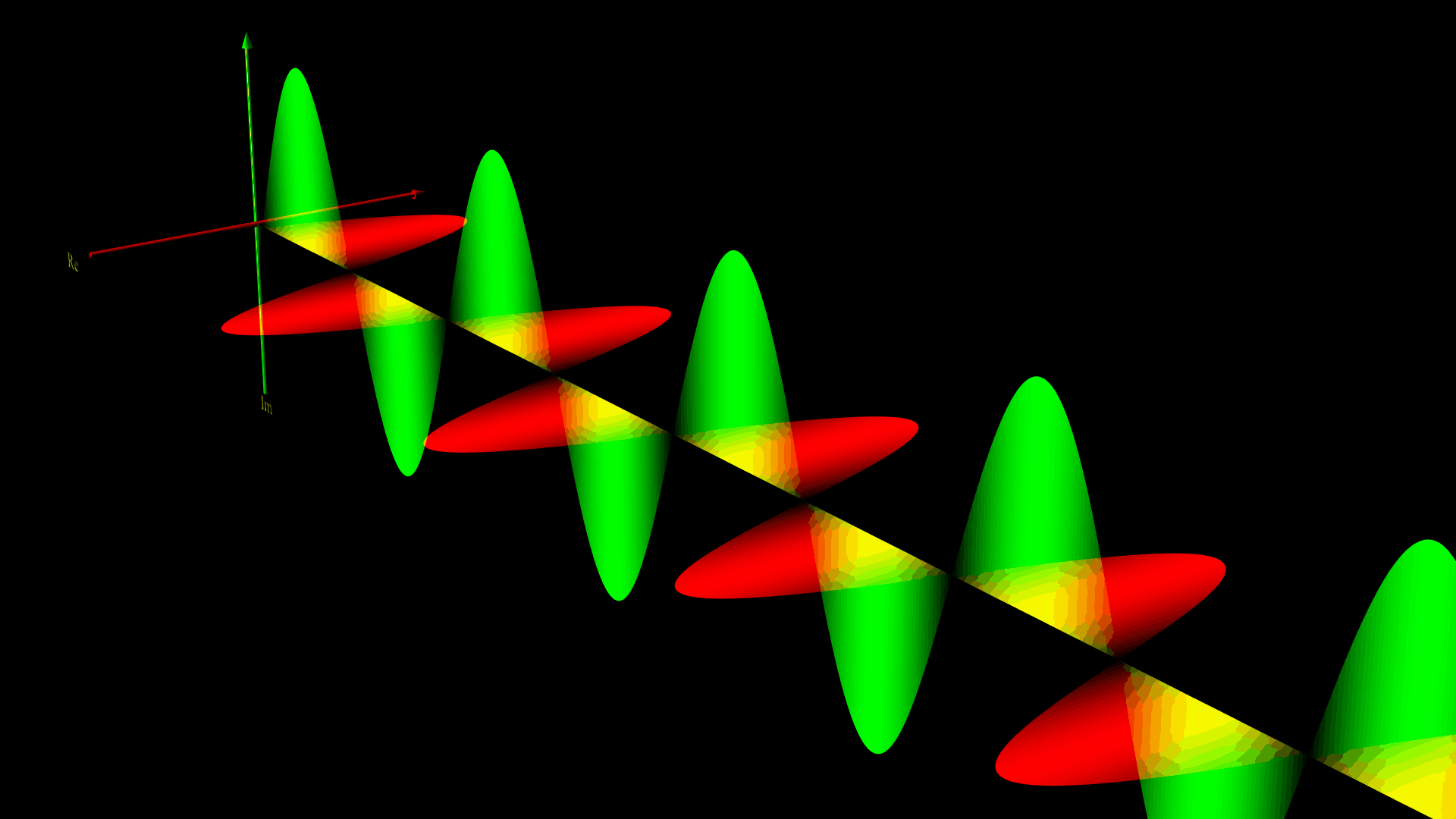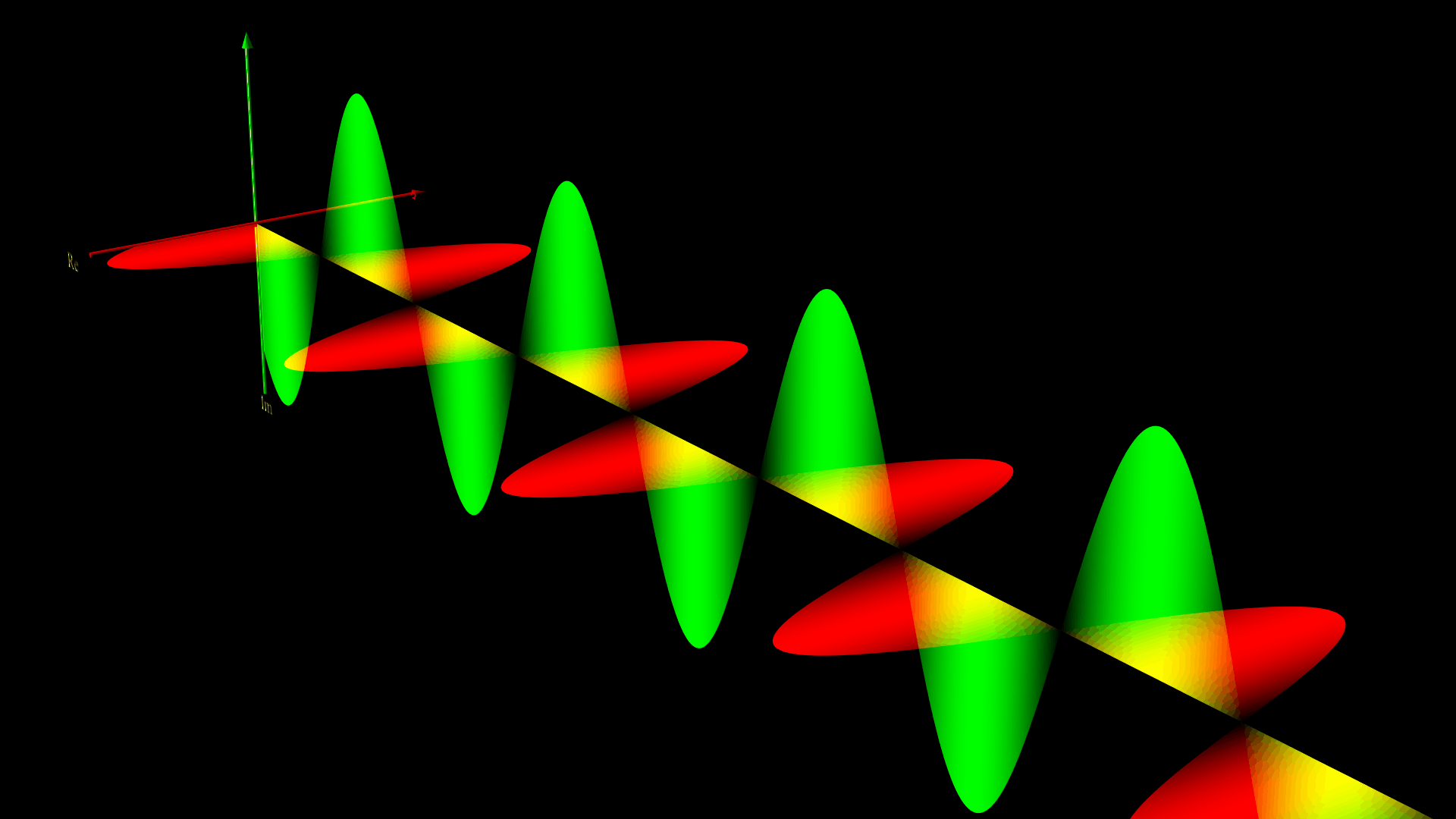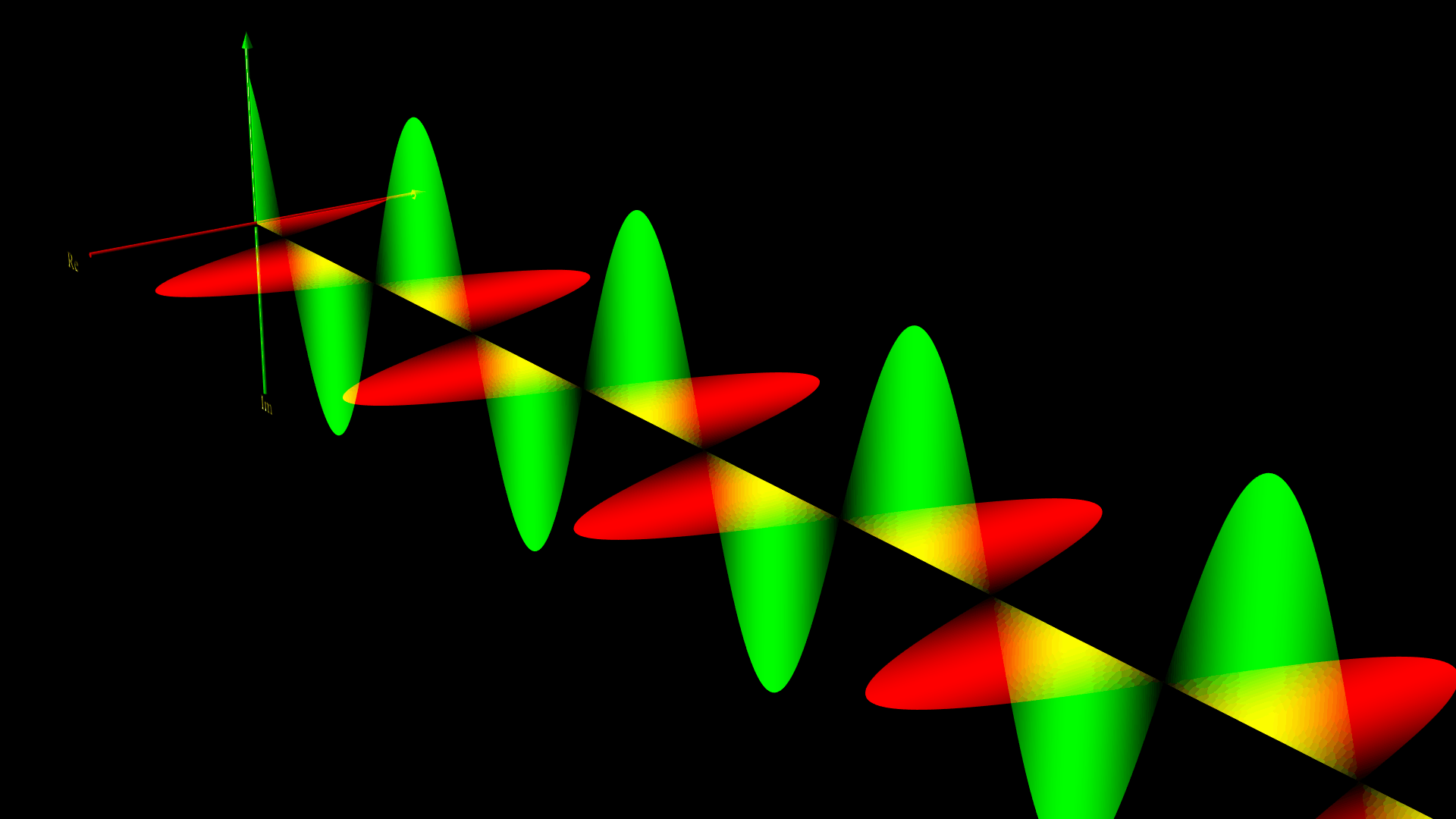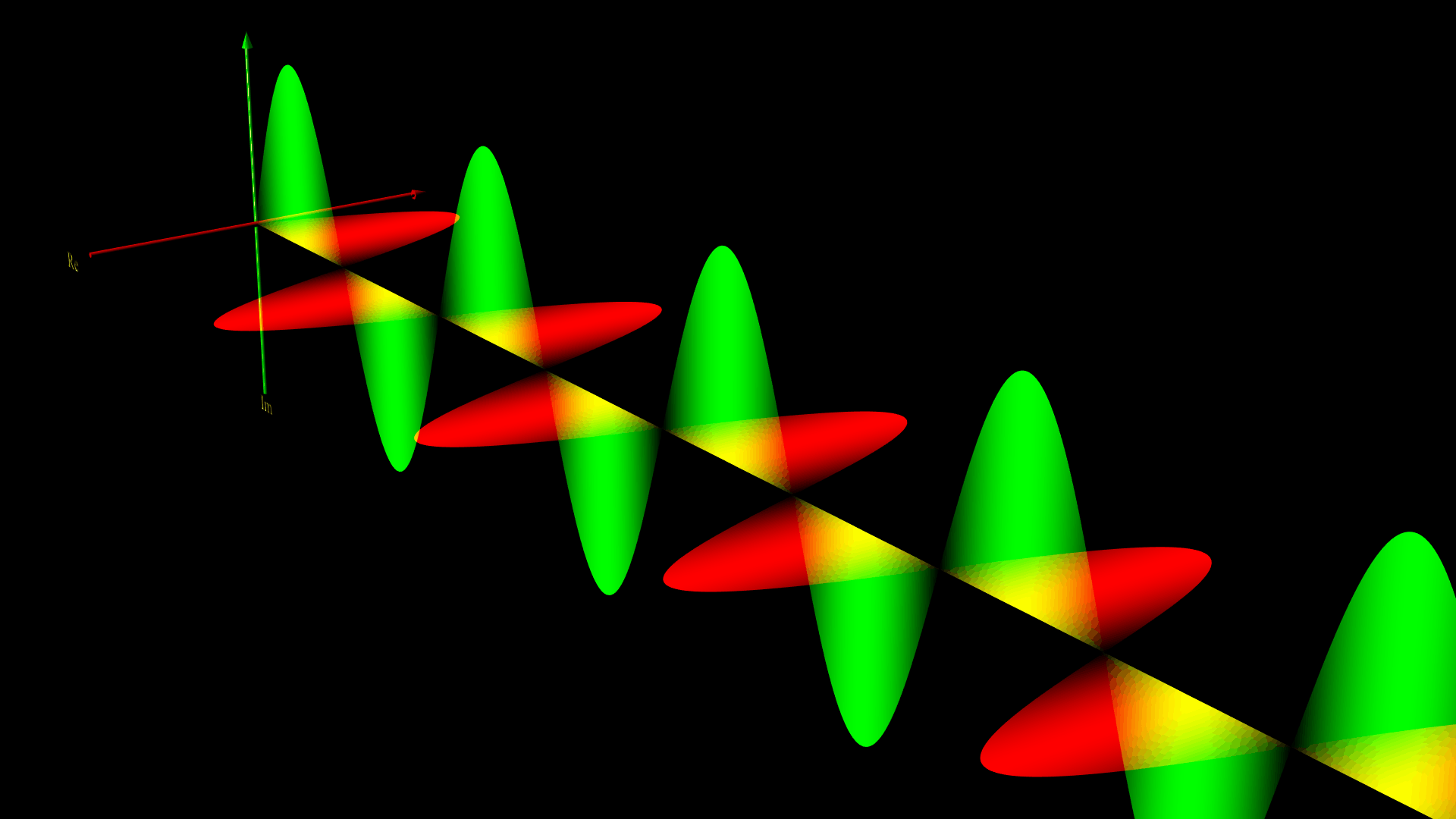
円偏光( $A_{y0} = A_{z0}$ かつ $\phi_z – \phi_y = \pm \pi/2$ )
円偏光(左回り)
下の図は、$ A_{y0} = A_{z0} = 1$ 、$\phi_z – \phi_y = \pi/2$ とした、ベクトルポテンシャルのグラフィックスだよ。

円偏光(右回り)
下の図は、$ A_{y0} = A_{z0} = 1$ 、$\phi_z – \phi_y = -\pi/2$ とした、ベクトルポテンシャルのグラフィックスだよ。

円偏光( $A_{y0} = A_{z0}$ かつ $\phi_z – \phi_y \ne \pm \pi/2$ )
下の図は、$ A_{y0} = A_{z0} = 1$ 、$\phi_z – \phi_y = \pi/4$ とした、ベクトルポテンシャルのグラフィックスだよ。

こんにちわ、とても為になるHPで、参考にさせて頂いております。
ひとつ、質問があるのですが、本HPの各種偏光のgifグラフィックを、解り易い偏光の図解として、別のHPに転載し、紹介させて頂いてもよろしいでしょうか?
返事が遅くなりまして申し訳ございませんでした。
全然問題ありません。
どうぞ!