前回示したスピノールの時間発展の表式に基づいて、数値計算を行ったので結果を示すよ。
次のグラフは、時間依存する磁場を $\boldsymbol{B}(t) = (0, B_y\sin(\omega t), B_z)$ で、$ B_y = B_z = 0.1 [{\rm T}]$、 $\omega = 2\omega_L$ として、ルンゲ・クッタ法を用いて、時間発展を計算した結果だよ。初期状態は下向きスピン100%、上向きスピン0%です。
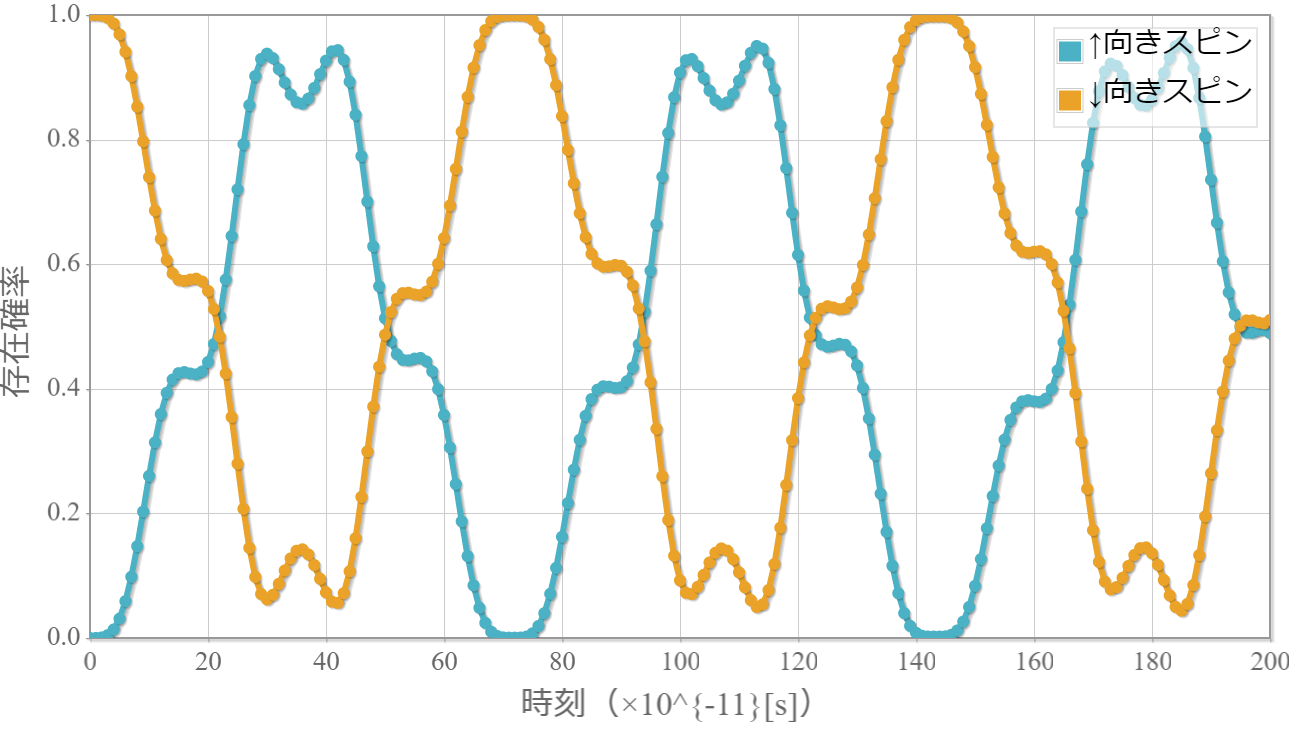
磁気共鳴によってスピンの向きが変化している様子が分かるね。でもラビ振動のように単純な形では無いけどね。
振動磁場の角振動数に対する遷移確率の最大値
次のグラフは、振動磁場の角振動数を $\bar{\omega} = 2\omega_L$ を基準として0から4まで変化させたときの遷移確率の最大値をプロットした結果だよ。
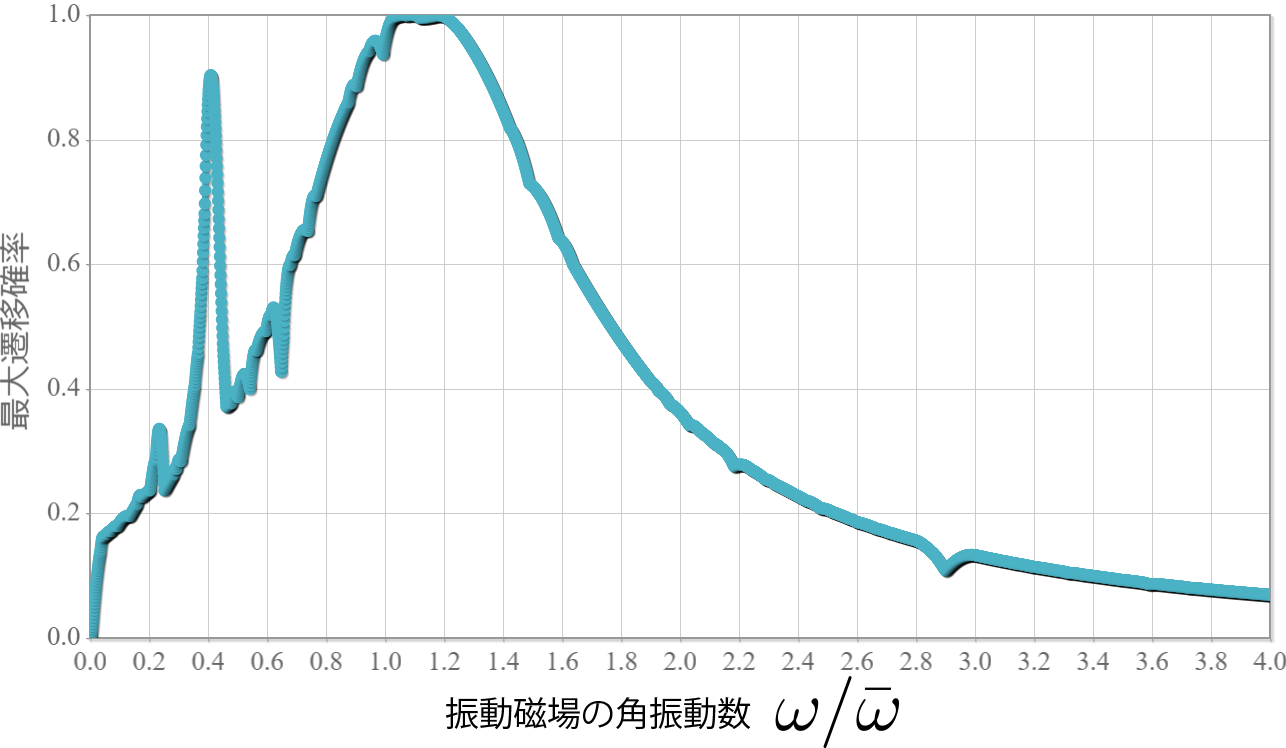
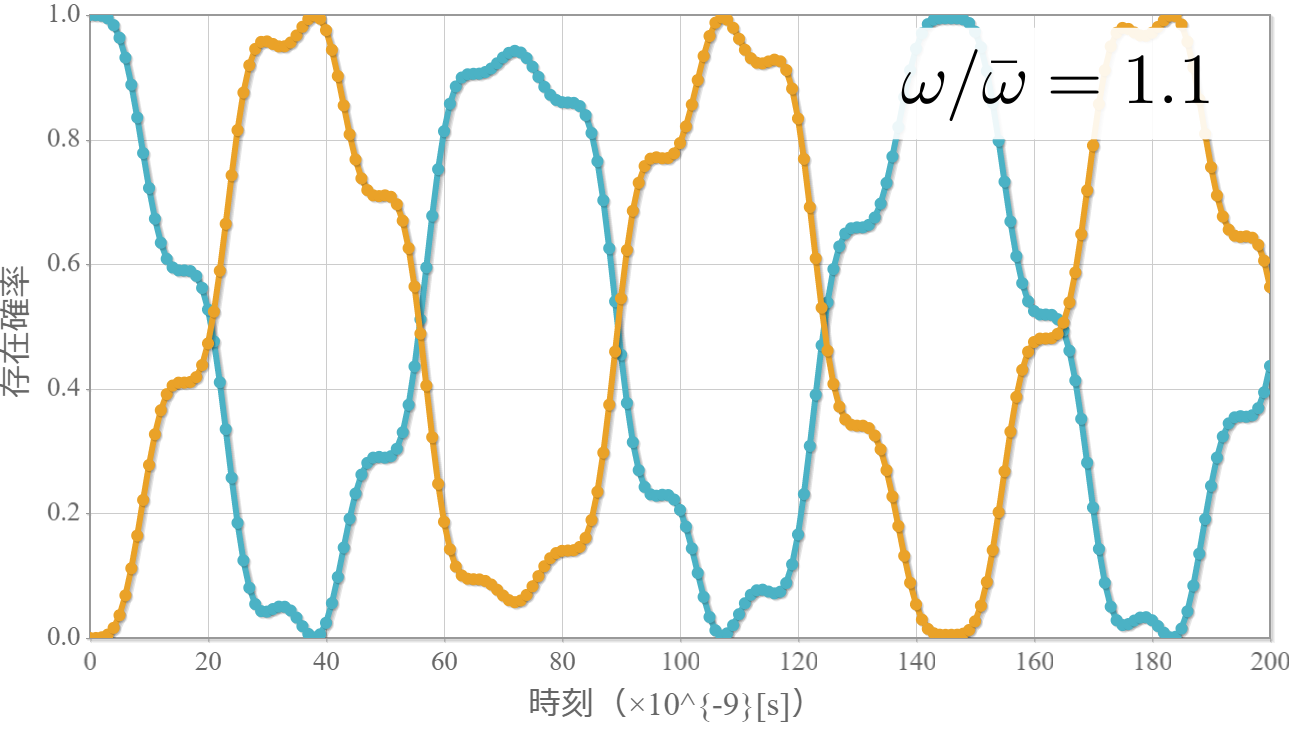
$\omega/\bar{\omega} = 1.0$ 過ぎから $1.2$ 手前までが、最大遷移確率が100%となっているね。次のグラフは、$\omega/\bar{\omega} =1.1$ としたときの、スピノールの時間変化の結果だよ。遷移確率が100%になっている時間があることが分かるね。

静磁場でもspinorは時間発展しますよ。
χ↑=cos α exp -iβ
χ↓=sin α exp iβ
と置いて、H=(eℏ/2m)B・S (Bは時間変化しない)とすると、
H = eℏ/4m [2 sin2α (B_x cos2β – B_y sin2β)+ B_z cos2α ]
となります。Hがβ依存性を持っているので、spinorの運動方程式
dα/dt=(1/ℏsin2α)(dH/dβ)
dβ/dt=(-1/ℏsin2α)(dH/dα)
にてαが時間的に変動し、Bのx成分とy成分が重要になります。