物理シミュレーションが趣味なシミュ君のページ
この前導出した水素原子の外場による光電効果の計算方法に基づいて計算した結果を示すよ。入射した電磁場の波長は $ \lambda = 10\, a_B $ （ $a_B$ はボーア半径、 $ E= E = 2343[{\rm eV}] $）。長さ $L$ の箱内で定義される平面波で展開したせいか、飛び出したはずの電子が、外場の影響を受けてまた基底状態に戻るっていう結果になってしまったよ。考えてみれば、これはラビ振動と全く同じ物理的な状況だね。
\[\begin{align}
i
\end{align}\tag{10}\]
前回、水素分子の固有状態の数値計算方法を示そうとしたけれども、展開する直交関数系を全く考慮していなかったために、異なる量子数で直交しないために固有値方程式を導出することができなかったね。今回は、水素分子イオンを構成する２つの原子核の重心位置（ $\boldsymbol{R}_0$ ）を基準とした水素様原子（$Z=2$）の固有関数系で展開する方法で考えてみるよ。
\begin{align}
\psi(\boldsymbol{r}) = \sum\limits_{nlm} a_{nlm} \varphi_{nlm}^{(Z)}(\boldsymbol{r}-\boldsymbol{R}_0)
\end{align}
この固有関数に合わせて、ハミルトニアンを次のように変形するよ。
\begin{align}
\hat{H} &\ = \left[ -\frac{\hbar^2}{2m_e} \nabla^2 – \frac{Ze^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{R}_0|} \right] + \left[ \frac{Ze^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{R}_0|} – \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_A|} – \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_B|} \right] \\\\
&\ = \hat{H}_0^{(Z)} + V(\boldsymbol{r})
\end{align}
このように変形することで、$ \hat{H}_0 \varphi_{nlm}^{(Z)} (\boldsymbol{r}-\boldsymbol{R}_0) = E_n^{(Z)} \varphi_{nlm}^{(Z)} (\boldsymbol{r}-\boldsymbol{R}_0) $ と固有状態となるね。シュレディンガー方程式 $\hat{H} \psi(\boldsymbol{r}) = E \psi(\boldsymbol{r})$ に代入してすると
\begin{align}
\sum\limits_{nlm} a_{nlm} \left[ E_n + V(\boldsymbol{r}) \right] \varphi_{nlm}^{(Z)} (\boldsymbol{r}-\boldsymbol{R}_0) = E \sum\limits_{nlm} a_{nlm} \varphi_{nlm}^{(Z)} (\boldsymbol{r}-\boldsymbol{R}_0)
\end{align}
となるので、いつものとおり、両辺に $ \varphi_{n’l’m’}^{(Z)*}(\boldsymbol{r}-\boldsymbol{R}_0)$ を掛けて全空間で積分すると、
\begin{align}
a_{n’l’m’} E_{n’} + \sum\limits_{nlm} a_{nlm} \langle n’,l’,m’| V(\boldsymbol{r}) | n, l, m \rangle = Ea_{n’l’m’}
\end{align}
となって、最も単純な固有値方程式の形になるね。ちなみに
\begin{align}
\langle n’,l’,m’| V(\boldsymbol{r}) | n, l, m \rangle &\ = \int \varphi_{n’l’m’}^{(Z)*}(\boldsymbol{r}-\boldsymbol{R}_0) V(\boldsymbol{r}) \varphi_{nlm}^{(Z)}(\boldsymbol{r}-\boldsymbol{R}_0) dV\\
\delta_{nn’}\delta_{ll’}\delta_{mm’} &\ = \int \varphi_{n’l’m’}^{(Z)*}(\boldsymbol{r}-\boldsymbol{R}_0) \varphi_{nlm}^{(Z)}(\boldsymbol{r}-\boldsymbol{R}_0) dV
\end{align}
だよ。このポテンシャル項を具体的に計算するために、原子核Aと原子核Bの重心位置を原点（$\boldsymbol{R}_0=0 $）、原子核Aを基準とした原子核Bの位置ベクトルを $\boldsymbol{R} = (R,0,0)$ として、改めてポテンシャル項を書き直すと次のようになるね。
\begin{align}
V(\boldsymbol{r}) = -\frac{e^2}{4\pi \epsilon_0} \left[ \frac{1}{|\boldsymbol{r} -\frac{1}{2}\boldsymbol{R}|} + \frac{1}{|\boldsymbol{r} + \frac{1}{2}\boldsymbol{R}|} – \frac{Z}{|\boldsymbol{r}|} \right]
\end{align}
次回は、この計算結果を示すよ。
右図で表したような、$Z=1$ の原子核２個の周りを回る電子１個となる水素分子イオンのエネルギー準位を計算するよ。２つの原子核は空間に固定されていると考えると、ハミルトニアンは次のようになるね。
\begin{align}
\hat{H} = -\frac{\hbar^2}{2m_e} \nabla^2 + \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_A|} + \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_B|}
\end{align}
今までと同様に、波動関数をそれぞれの原子を基準とした水素原子の固有状態 $\varphi_{nlm}$ で次のように表すことができると考えるよ。
\begin{align}
\psi(\boldsymbol{r}) = \sum\limits_{nlm} \left[ C^{(A)}_{nlm} \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_A) +C^{(B)}_{nlm} \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_B) \right]
\end{align}
これをシュレディンガー方程式 $\hat{H}\psi(\boldsymbol{r}) = E\psi(\boldsymbol{r})$ に代入すると
\begin{align}
\sum\limits_{nlm} C^{(A)}_{nlm} \left[ E_n + \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_B|} \right] \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_A) &\ +\sum\limits_{nlm} C^{(B)}_{nlm} \left[ E_n + \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_A|} \right] \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_B) \\
&\ = E \sum\limits_{nlm} \left[ C^{(A)}_{nlm} \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_A) +C^{(B)}_{nlm} \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_B) \right]
\end{align}
となるね。ここから係数を計算するための固有値方程式を導入するために、両辺に $\varphi_{nlm}^*(\boldsymbol{r} -\boldsymbol{r}_A)$ と $\varphi_{nlm}^*(\boldsymbol{r} -\boldsymbol{r}_B)$ をそれぞれ掛けて全空間で積分するけれども、その際に「異なる量子数」に対する空間積分が直交してほしいけれども、きっと直交しないね。
\begin{align}
C^{(A)}_{n’l’m’} E_{n’} + \frac{e^2}{4\pi \epsilon_0 } \sum\limits_{nlm} C^{(A)}_{nlm} {}_A\!\langle n’,l’,m’| \frac{1}{| \boldsymbol{r} -\boldsymbol{r}_B|} |n,l,m\rangle\!{}_A &\ +\sum\limits_{nlm} C^{(B)}_{nlm} \left[ E_n {}_A\!\langle n’,l’,m’|n,l,m\rangle\!{}_B + {}_A\!\langle n’,l’,m’| \frac{1}{| \boldsymbol{r} -\boldsymbol{r}_A|}|n,l,m\rangle\!{}_B \right] \\
&\ = E \left[ C^{(A)}_{n’l’m’} + \sum\limits_{nlm} C^{(B)}_{nlm} {}_A\!\langle n’,l’,m’|n,l,m\rangle\!{}_B \right]
\end{align}
いつもどおりに固有値方程式の導出を試みたけれども、やっぱり直交しないことがネックとなって、うまくいかないね。もうちょっと工夫してみるね。
前回を踏まえて、ヘリウム原子基底状態の動径確率密度分布を計算したので、報告するよ。次のグラフでは、ヘリウム原子基底状態に対する動径確率密度分布は２種類用意したよ。１つ目は「２つの電子のどちらかがその距離にいる確率密度（ 青色：$\bar{P}_{100}^{Z=2}(r) $ ）」、２つ目は「１つの電子が原点にいて、もう一つの電子がその距離にいる確率密度（ 橙色：$P_{100}^{Z=2}(0,r) $ ）」。あと比較対象として、「水素原子基底状態に対する動径確率密度分布（$P_{100}^{Z=1}(r) $）」と「ヘリウム原子イオンの基底状態に対する動径確率密度分布（$P_{100}^{Z=2}(r) $）」を同時にプロットしたよ。
横軸が原点からの距離、縦軸が確率密度だよ。一番強く原子核に束縛されているのが「ヘリウム原子イオンの基底状態」で、反対に最も束縛されていないのが「水素原子の基底状態」だね。つまり、原子核の電荷が $Z=2$ で電子が１個の場合が一番強く束縛されて、$Z=1$ で電子が１個の場合が最も束縛が弱いね。２種類用意したヘリウム原子を比較すると、１個を原点に存在する「橙色：$P_{100}^{Z=2}(0,r) $」は、他方の「青色：$\bar{P}_{100}^{Z=2}(r) $」と比較して、電子間の反発でより遠くに存在することがわかるね。
この前、水素原子の外場による光電効果の数値計算方法を導出したけれども、この表式では、放出した電子は外場の影響をうけてしまって、放出方向がわからなくなってしまうね。今回はもう少し物理的な描像がわかりやすくなるような表式の導入を行うよ。波動関数を初期状態とする水素原子の基底状態 $\varphi_{100}$ と飛び出した電子の平面波を表す項の２つで
\begin{align}
\psi(\boldsymbol{r}, t) = a(t) \varphi_{100}(\boldsymbol{r}) + \sum\limits_{\boldsymbol{n}}’b_{\boldsymbol{n}}(t) \frac{1}{\sqrt{V}} \, e^{i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}
と表すとするよ。ただし、$ \boldsymbol{k} = \frac{2\pi}{L}(n_x, n_y, n_z) $ で、$L$ は空間サイズで $V =L^3$、 $\boldsymbol{n} = (n_x, n_y, n_z)$ は整数だよ。注意する点は、上記の和はすべての $\boldsymbol{n}$ で取らずに、基底状態 $\varphi_{100}(\boldsymbol{\boldsymbol{r}})$ の波数成分
\begin{align}
\varphi_{100}(\boldsymbol{\boldsymbol{k}}) = \frac{1}{\sqrt{V}} \int \varphi_{100}(\boldsymbol{r})e^{-i\boldsymbol{k}\cdot\boldsymbol{r}} dV
\end{align}
を含まない $\boldsymbol{n}$ に限って和を取るという制限をつけるよ。そうすることで、
\begin{align}
\int \varphi_{100}(\boldsymbol{r})e^{-i\boldsymbol{k}\cdot\boldsymbol{r}} dV = 0
\end{align}
というふうに、基底状態と平面波が直交すると考えることができるからね。これをハミルトニアン
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}} =\hat{H}_0 + \frac{e}{im_e}
\,\boldsymbol{A}\cdot\nabla
\end{align}
とするシュレーディンガー方程式
\begin{align}
i\hbar\frac{\partial}{\partial t} \psi(\boldsymbol{r}, t) = \hat{H} \psi(\boldsymbol{r}, t)
\end{align}
に代入した
\begin{align}
i\hbar \left[\varphi_{100}(\boldsymbol{r}) \frac{d a(t)}{d t} + \sum\limits_{\boldsymbol{n}}’ \frac{1}{\sqrt{V}} \, e^{i\boldsymbol{k}\cdot\boldsymbol{r}} \frac{d b_{\boldsymbol{n}}(t)}{dt} \right] = a(t) \left(E_{100} +\frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}}\right)\varphi_{100}(\boldsymbol{r}) + \left( \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}} \right) \sum\limits_{\boldsymbol{n}}’b_{\boldsymbol{n}}(t) \frac{1}{\sqrt{V}} \, e^{i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}
から出発して、展開係数 $a(t)$ と $b_{\boldsymbol{n}}(t)$ の時間発展の表式を導出するよ。ちなみに、外場は波数ベクトル $\boldsymbol{K}$、角振動数 $\omega$ のベクトルポテンシャル
\begin{align}
\boldsymbol{A} = \boldsymbol{A}_0 \left[ e^{i\boldsymbol{K}\cdot\boldsymbol{r} – i\omega t} + e^{-i\boldsymbol{K}\cdot\boldsymbol{r} + i\omega t}\right]
\end{align}
で表すよ。ただし、分散関係は電磁波なので光速 $c$ を用いて $\omega = cK$ となるよ。
先の基底状態と平面波の直交性と、$\hat{\boldsymbol{p}}/m_e = [ \hat{H}_0,\boldsymbol{r}]/i\hbar $を考慮して、両辺に $\varphi_{100}^*(\boldsymbol{r})$ を掛けて全空間で積分すると次のようになるよ。
\begin{align}
i\hbar \frac{d a(t)}{d t} = E_{100}a(t) + \frac{\hbar e}{im_e}\sum\limits_{\boldsymbol{n}}’b_{\boldsymbol{n}}(t)\frac{1}{\sqrt{V}} \int \varphi_{100}^*(\boldsymbol{r}) \boldsymbol{A}\cdot \nabla e^{i\boldsymbol{k}\cdot\boldsymbol{r}} dV
\end{align}
第２項目の積分は
\begin{align}
\frac{1}{\sqrt{V}} \int \varphi_{100}^*(\boldsymbol{r}) \boldsymbol{A}\cdot \nabla e^{i\boldsymbol{k}\cdot\boldsymbol{r}} dV &\ = i\boldsymbol{A}_0\cdot\boldsymbol{k} \left[ \frac{1}{\sqrt{V}} \int \varphi_{100}^*(\boldsymbol{r}) e^{i(\boldsymbol{k}+\boldsymbol{K})\cdot\boldsymbol{r}} dV e^{-i\omega t } + \frac{1}{\sqrt{V}} \int \varphi_{100}^*(\boldsymbol{r}) e^{i(\boldsymbol{k}-\boldsymbol{K})\cdot\boldsymbol{r}} dV e^{i\omega t } \right] \\
&\ = i\boldsymbol{A}_0\cdot\boldsymbol{k} \left[ \varphi_{100}^*(\boldsymbol{k}+\boldsymbol{K})e^{-i\omega t } +\varphi_{100}^*(\boldsymbol{k} – \boldsymbol{K})e^{i\omega t } \right]
\end{align}
と表すことができるので、これを元の式に代入した
\begin{align}
i\hbar \frac{d a(t)}{d t} = E_{100}a(t) + \frac{\hbar e}{m_e}\sum\limits_{\boldsymbol{n}}’ \boldsymbol{A}_0\cdot\boldsymbol{k} \left[ \varphi_{100}^*(\boldsymbol{k}+\boldsymbol{K})e^{-i\omega t } +\varphi_{100}^*(\boldsymbol{k} – \boldsymbol{K})e^{i\omega t } \right]b_{\boldsymbol{n}}(t)
\end{align}
が、係数 $a(t)$ に対する常微分方程式だね。この式はひとまず置いておくよ。
今度は、平面波の展開係数に関する表式を得るために、両辺に $\frac{1}{\sqrt{V}} e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}}$ を掛けて全空間で積分するよ。基底状態と平面波の直交性を考慮すると次のようになるよ。
\begin{align}
i\hbar \frac{d b_{\boldsymbol{n}’}(t)}{d t} = a(t) \frac{\hbar e}{m_e}\frac{1}{\sqrt{V}} \int e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}} \boldsymbol{A}\cdot \hat{\boldsymbol{p}} \varphi_{100}(\boldsymbol{r}) dV + \sum\limits_{\boldsymbol{n}}’b_{\boldsymbol{n}}(t)\, \frac{1}{V}\int e^{-i\boldsymbol{k}’\cdot\boldsymbol{r} } \left( \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}} \right) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} dV
\end{align}
この内、まず右辺第２目は、平面波同士の相互作用を表しているね。もう少し具体的に言うと、$H_0$ 因子は原子核の存在による変化、$\boldsymbol{A}\cdot \hat{\boldsymbol{p}}$ 因子は外場による変化を表しているね。今回は、光電効果に着目するので、電離したあとの電子は、原子核や外場の影響を受けずににまっすぐ進んでと想定したいので、この項を無視するね。
次に、第１項目だけれども、この積分は先に導出した積分と非常によく似ているね。部分積分を行って整理すると
\begin{align}
\frac{1}{\sqrt{V}} \int e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}\varphi_{100}(\boldsymbol{r}) dV
&\ = i \boldsymbol{A}_0\cdot \boldsymbol{k}’\left[ \frac{1}{\sqrt{V}} \int \varphi_{100}(\boldsymbol{r}) e^{-i(\boldsymbol{k}’-\boldsymbol{K})\cdot\boldsymbol{r}} dV e^{-i\omega t } + \frac{1}{\sqrt{V}} \int \varphi_{100}(\boldsymbol{r})e^{-i(\boldsymbol{k}’+\boldsymbol{K})\cdot\boldsymbol{r}} dV e^{i\omega t } \right]\\
&\ = i\boldsymbol{A}_0\cdot\boldsymbol{k}’ \left[ \varphi_{100}(\boldsymbol{k}’-\boldsymbol{K})e^{-i\omega t }
+\varphi_{100}(\boldsymbol{k}’ + \boldsymbol{K})e^{i\omega t } \right]
\end{align}
と表すことができるので、これを元の式に代入した
\begin{align}
i\hbar \frac{d b_{\boldsymbol{n}’}(t)}{d t} = \frac{\hbar e}{m_e} \boldsymbol{A}_0\cdot\boldsymbol{k}’ \left[ \varphi_{100}(\boldsymbol{k}’-\boldsymbol{K})e^{-i\omega t }
+\varphi_{100}(\boldsymbol{k}’ + \boldsymbol{K})e^{i\omega t } \right]a(t)
\end{align}
以上をまとめると、基底状態の係数 $a(t)$ と平面波の展開係数 $b_{\boldsymbol{n}}(t)$ は連立常微分方程式
\begin{align}
i\hbar \frac{d a(t)}{d t} &\ = E_{100}a(t) + \frac{\hbar e}{m_e}\sum\limits_{\boldsymbol{n}}’
\boldsymbol{A}_0\cdot\boldsymbol{k} \left[ \varphi_{100}^*(\boldsymbol{k}+\boldsymbol{K})e^{-i\omega t }
+\varphi_{100}^*(\boldsymbol{k} – \boldsymbol{K})e^{i\omega t } \right]b_{\boldsymbol{n}}(t)\\
i\hbar \frac{d b_{\boldsymbol{n}’}(t)}{d t} &\ = \frac{\hbar e}{m_e} \boldsymbol{A}_0\cdot\boldsymbol{k}’ \left[ \varphi_{100}(\boldsymbol{k}’-\boldsymbol{K})e^{-i\omega t }+\varphi_{100}(\boldsymbol{k}’ + \boldsymbol{K})e^{i\omega t } \right]a(t)
\end{align}
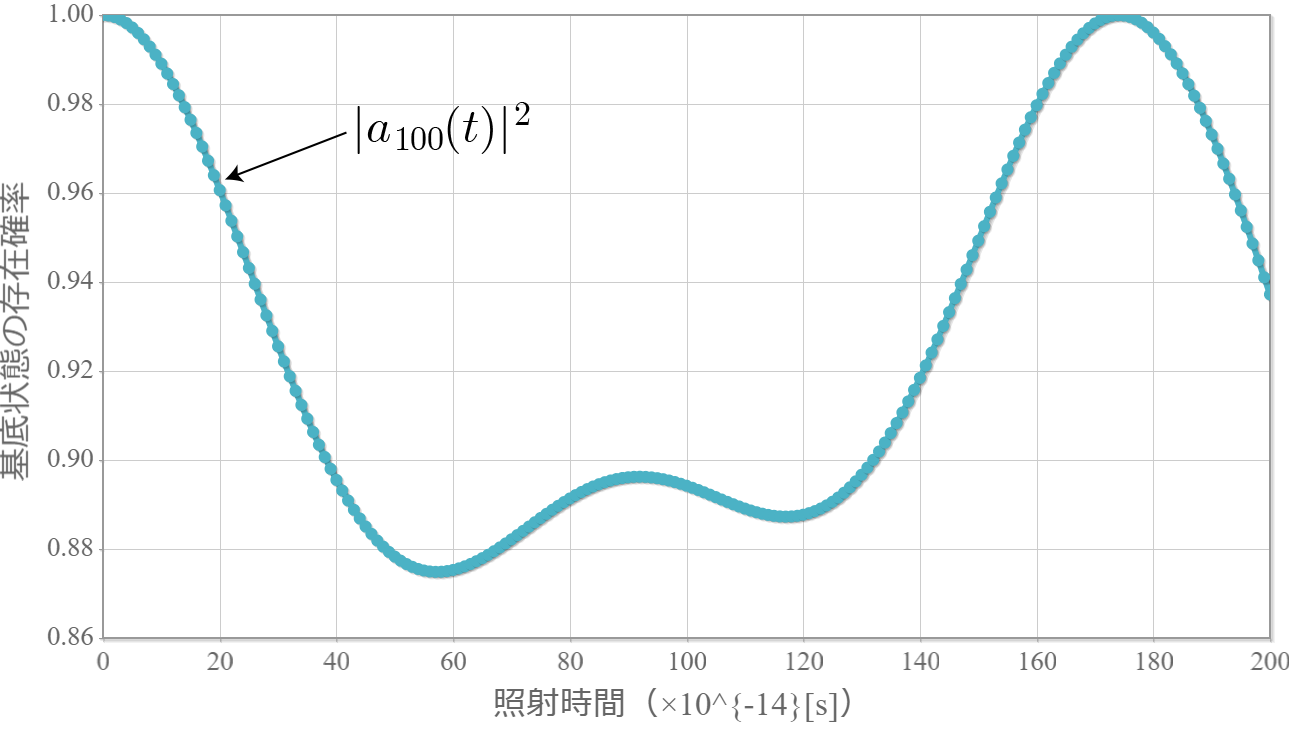
に従って時間発展するね。基底状態のフーリエ変換はすでに計算しているのでこれを利用して、初期条件を $a(0)=1$、$b_{\boldsymbol{n}}(0) =0$ として、時刻が大きくなるに連れて、$|a(t)|^2$ が小さくなって行くに従って $b_{\boldsymbol{n}}(t)$ が大きくなることが想定されるね。そのときの $\boldsymbol{n}$ の分布が電子が飛び出していく方向を表すよ。次回は実際に計算してみるよ。
「ヘリウム原子のエネルギー固有状態の計算方法」に基づいて、ヘリウム原子のエネルギー準位と固有関数の空間分布を計算したよ。「ヘリウム原子の基底状態の計算結果」で示したとおり、計算結果はよく知られた精密な実験結果とかなり一致しているよ。
次の図は、パラ（対称関数・スピン１重項）とオルト（反対称関数・スピン３重項）の主量子数 $n=1,2,3$
のエネルギー準位だよ。オルトのほうがパラよりも若干小さな値となるね。これは交換相互作用の結果だね。イオン化エネルギーは、電子２個の基底状態から電子１個を引き離すために必要なエネルギーで、「基底状態エネルギー（$-79.18[{\rm
eV}]$）」から「電子が１個のみのヘリウム原子の基底状態エネルギー（ $-54.4[{\rm eV}]$ ）」で計算できるよ。
今回も独立電子近似の場合と同様、粒子の１つが
$\varphi_{100}(\boldsymbol{r})|$の最も確率の高い原点（ $\boldsymbol{r}_1=0$ あるいは $\boldsymbol{r}_2=0$
）に存在するとして、他方の粒子の空間確率密度を描画するよ。最初の表がパラヘリウム（対称関数・スピン1重項）、次の表がオルトヘリウム（反対称関数・スピン3重項）だよ。
（※実際の表はこちらのページを見てね！）
ちなみにヘリウム原子の場合、直交関数系は $(1,0,0)$ を必ず含むよ。なぜならば、$(1,0,0)$ から次に低い $(2,0,0)$ とした場合の固有エネルギーは約 $-20[{\rm eV}]$
で、イオン化エネルギーよりも高くなるために実質的には先に電離してしまうね。
水素原子の電子に直線偏光の電磁波（古典）を入射したときの状態遷移は以前解説したね。今回は、入射した電磁波の振動数を高めることで生じる「光電効果」（束縛状態の電子が外場によって非束縛状態へ遷移する効果）をシミュレーションするのに必要な表式を導出するよ。スピンと外場の２次の項を無視したハミルトニアンは、
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}} = -\frac{\hbar^2}{2m_e}\nabla^2 + V(r) + \frac{e}{im_e} \,\boldsymbol{A}\cdot\nabla
\end{align}
となるね。このハミルトニアンを用いたシュレディンガー方程式
\begin{align}
i\hbar\frac{\partial}{\partial t} \psi(\boldsymbol{r}, t) = \hat{H} \psi(\boldsymbol{r}, t)
\end{align}
だね。ここから出発するよ。今回は、水素原子核に束縛された状態からとき放たれた状態も考慮するため、波動関数は波数空間で展開した
\begin{align}
\psi(\boldsymbol{r}, t) = \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z} a_{n_xn_yn_z}(t)\, e^{i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}
で表すよ。ただし、$ \boldsymbol{k} = \frac{2\pi}{L}(n_x, n_y, n_z) $ で、$L$ は空間サイズで $V =L^3$、 $n_x, n_y, n_z$ は整数だよ。これをシュレディンガー方程式に代入して、両辺に $\frac{1}{\sqrt{V}}e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}}$ を掛けて、全空間で積分すると
\begin{align}
i\hbar\frac{d a_{n_x’n_y’n_z’}(t)}{d t} = \left[ \frac{\hbar^2k’^2}{2m_e} + \frac{e}{m_e} \,\boldsymbol{A}\cdot \boldsymbol{k}’ \right] a_{n_x’n_y’n_z’}(t) + \frac{1}{V}\sum\limits_{n_x, n_y, n_z} \left[ \int e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}} V(r) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} dV \right] a_{n_xn_yn_z}(t)
\end{align}
となるね。さらにポテンシャル項もついでに
\begin{align}
V(r) = \frac{1}{\sqrt{V}}\sum\limits_{n”_x, n”_y, n”_z} v_{n”_xn”_yn”_z}\, e^{i\boldsymbol{k}”\cdot\boldsymbol{r}}
\end{align}
と展開して代入すると、空間積分を実行することができて、次のような形になるね。
\begin{align}
i\hbar\frac{d a_{n_x’n_y’n_z’}(t)}{d t} = \left[ \frac{\hbar^2k’^2}{2m_e} + \frac{e}{im_e} \,\boldsymbol{A}\cdot \boldsymbol{k}’ \right] a_{n_x’n_y’n_z’}(t) + \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z}\,v_{n_x’-n_x,n_y’-n_y,n_z’-n_z} a_{n_xn_yn_z}(t)
\end{align}
さらに、クーロンポテンシャル $ V(r) = -e^2/4\pi\epsilon r$のように $1/r$ の場合には、展開係数 $ v_{n”_xn”_yn”_z} $ は解析的に導出することができて、
\begin{align}
v_{n”_xn”_yn”_z} = \frac{1}{\sqrt{V}} \int V(r)e^{-i\boldsymbol{k}”\cdot\boldsymbol{r}} dV = -\frac{e^2}{4\pi\epsilon_0} \, \frac{1}{k”^2}
\end{align}
で与えられるので、最終的には
\begin{align}
i\hbar\frac{d a_{n_x’n_y’n_z’}(t)}{d t} = \left[ \frac{\hbar^2k’^2}{2m_e} + \frac{e}{im_e} \,\boldsymbol{A}\cdot \boldsymbol{k}’ \right] a_{n_x’n_y’n_z’}(t) -\frac{e^2}{4\pi\epsilon_0}\, \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z}\,\frac{1}{k_{n_x’-n_x,n_y’-n_y,n_z’-n_z}^2 }a_{n_xn_yn_z}(t)
\end{align}
となるね。これで、$a_{n_xn_yn_z}$ に関する連立常微分方程式になるね。あとは、外場を与えるベクトルポテンシャル $\boldsymbol{A}$ を計算対象の系に合わせて設定して、ルンゲ・クッタ法を用いて時間発展を計算することができるね。ちなみに、$a_{n_xn_yn_z}$ の初期状態は、
\begin{align}
a_{n_xn_yn_z}(0) = \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z} \psi(\boldsymbol{r}, 0) \, e^{-i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}
で計算することができるので、例えば、$\psi(\boldsymbol{r}, 0) = \varphi_{100}$ と与えることで、初期状態を基底状態とした場合の計算を行うことができるよ。次回は結果を示すよ。
あとで、電磁波（古典）による「光電効果」（束縛状態の電子が外場によって非束縛状態へ遷移する効果）をシミュレーションしたいので、その準備として、水素原子に束縛された固有状態のフーリエ変換を数値的に調べておくよ。$ \boldsymbol{k} = \frac{2\pi}{L}(n_x, n_y, n_z) $ で、$L$ は空間サイズで $V =L^3$、 $n_x, n_y, n_z$ は整数として、固有状態の波数成分 $\varphi_{nlm}( \boldsymbol{k} )$ は、
\begin{align}
\varphi_{nlm}( \boldsymbol{k} ) = \frac{1}{\sqrt{V}} \int \varphi_{nlm}( \boldsymbol{r} ) e^{-i \boldsymbol{k} \cdot \boldsymbol{r} }dV
\end{align}
で表すことができるね。とりあえず、基底状態 $\varphi_{100}( \boldsymbol{k} ) $ の波数空間分布を示すよ（ $\varphi_{100}( \boldsymbol{k} ) $ の $kx-ky$ 平面上の値を、大きさは不透明度、位相は色で表しているよ）。
独立電子近似の場合、ヘリウム原子の２つの電子の波動関数は、個々の水素様原子（ $Z=2$ ）の波動関数の積を用いて、空間対称（スピン３重項／パラ）あるいは空間反対称（スピン１重項／オルト）の２つの状態をとるよ。具体的な波動関数の表式はそれぞれ
\begin{align}
\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) + \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) – \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\end{align}
と表されるね。この波動関数は各粒子ごとに３次元で合計で６次元の関数なので、これを描画するには工夫が必要になるよ。１番基本的な考え方は、空間位置 $ \boldsymbol{r} $ に粒子１あるいは粒子２が存在する空間確率密度を
\begin{align}
\rho( \boldsymbol{r} ) = \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}) |^2 dV_1 + \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, \boldsymbol{r}_2) |^2 dV_2
\end{align}
と定義することで、空間分布を計算することができるね。ただし、これを先の $\chi^{(S)}$ と $\chi^{(A)}$ に適用すると、
\begin{align}
\rho^{(S)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2\\
\rho^{(A)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2
\end{align}
となって、それぞれの粒子の空間分布の和となるね。ヘリウム原子の低エネルギーの状態は、粒子の片方は必ず $(n,l,m)=(1,0,0)$ に存在するので、先の空間確率密度を数値的に計算すると、他方の粒子がどの準位に存在したとしても、 $|\varphi_{100}(\boldsymbol{r})|^2 >> |\varphi_{nlm}(\boldsymbol{r})|^2 $ となって、実質的に $|\varphi_{100}(\boldsymbol{r})|^2$ となってしまうね。これは、２つの粒子が存在する確率が $|\varphi_{100}(\boldsymbol{r})|^2$ で表される領域に集中していることを意味しているよ。
そこで今回は、粒子の１つが $\varphi_{100}(\boldsymbol{r})|$の最も確率の高い原点（ $\boldsymbol{r}_1=0$ あるいは $\boldsymbol{r}_2=0$ ）に存在するとして、他方の粒子の空間確率密度
\begin{align}
\rho^{(S)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, 0)|^2 \\
\rho^{(A)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r},0)|^2
\end{align}
を定義して、空間分布を描画したよ。ちなみに両者とも第１項目と第２項目の値は同じ値となるよ。
（※実際の表はこちらのページを見てね！）
上記の結果は単に $|\varphi_{nlm}(\boldsymbol{r})|^2$ を計算した結果に似ているけれども異なるよ。空間対称関数と空間反対称関数では、概ね同じだけれども顕著に異なるのが、２個目の粒子の状態が $(n,l,m) =(2,0,0)$ や $(n,l,m) =(3,0,0)$ で、原点を中心に存在する場合だね。これは、空間対称関数の場合には、同じ領域に居ようとするけれども、空間反対称関数の場合には、互いに避けようとする結果だね。次回は、電子間の相互作用を加味した波動関数を描画するよ。