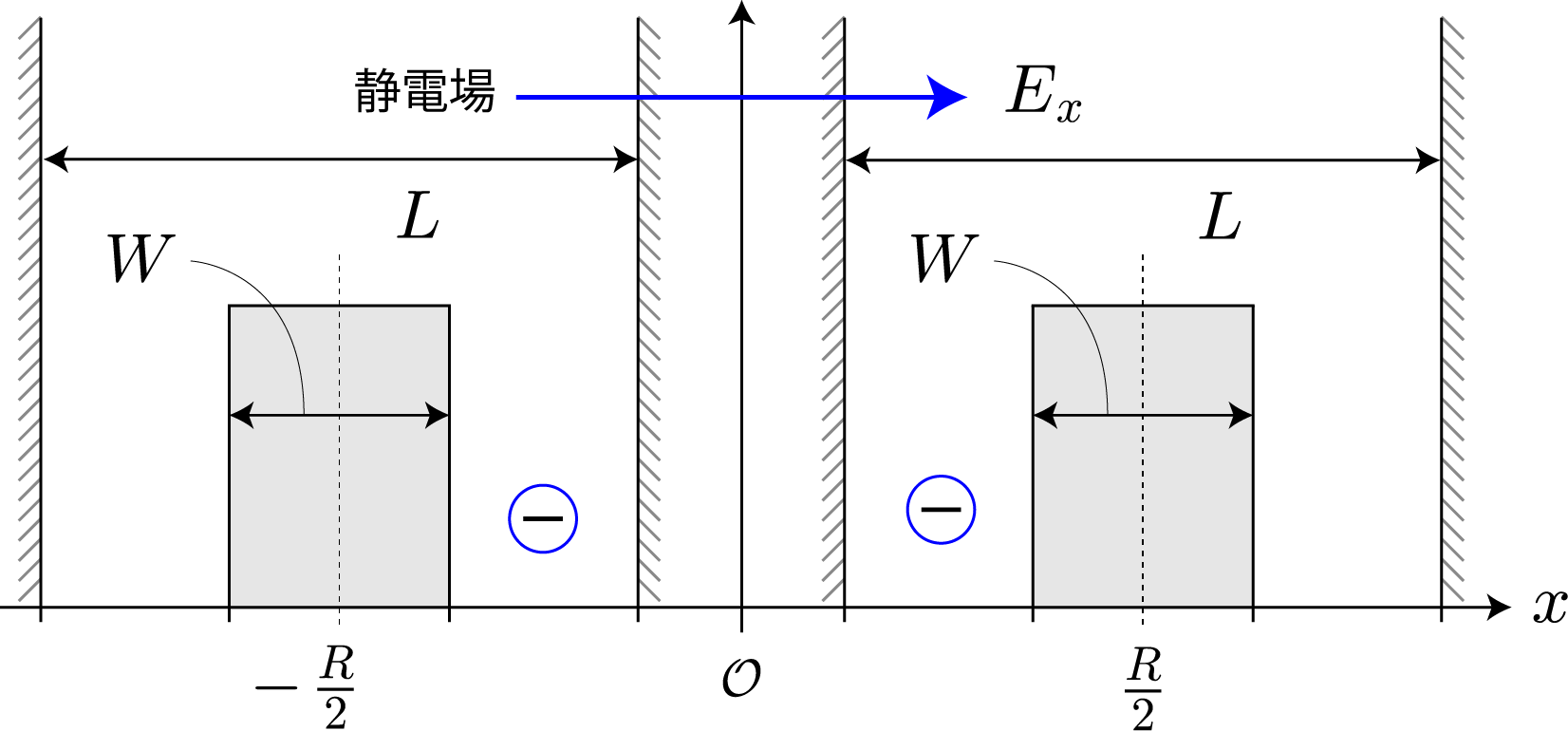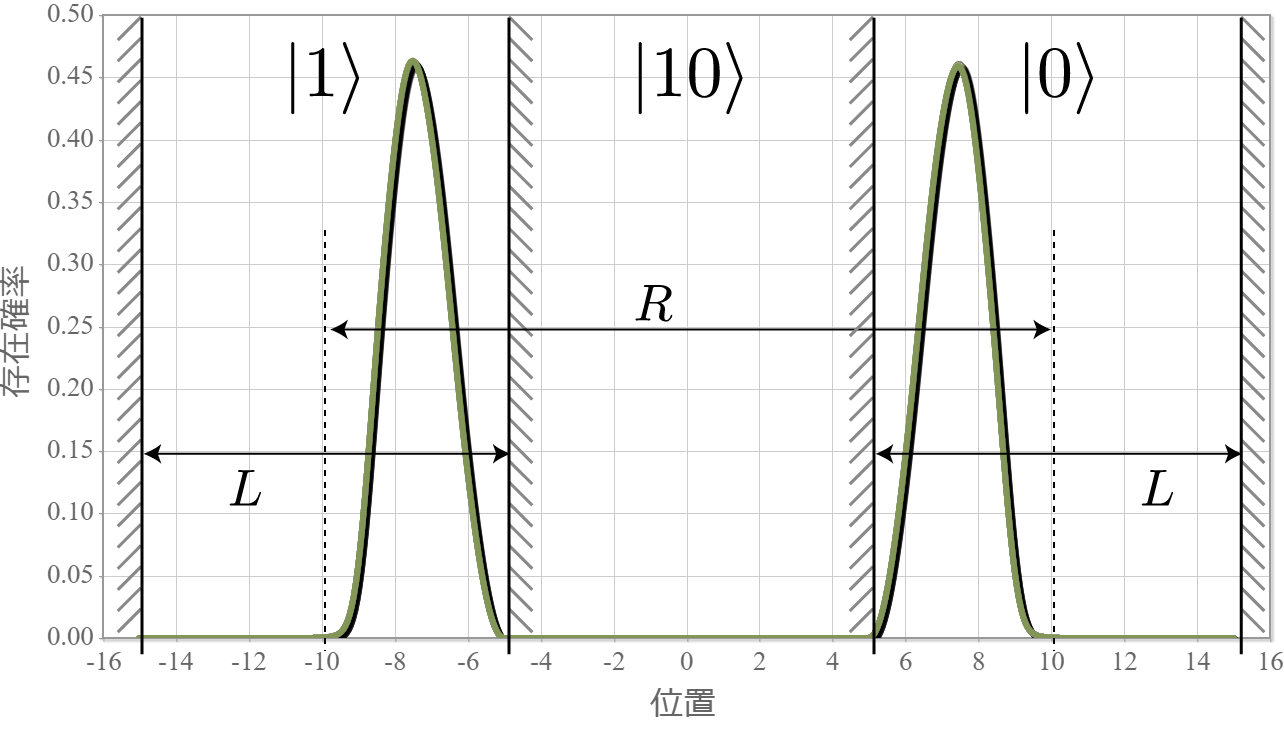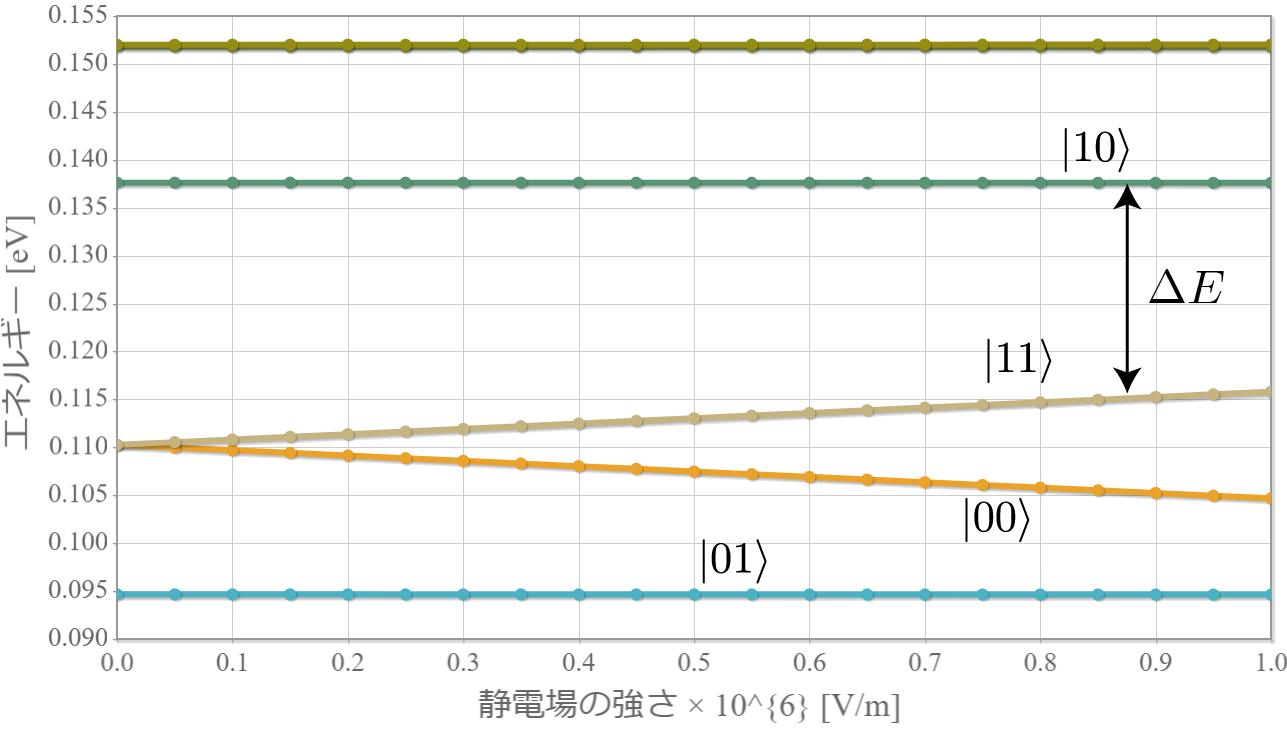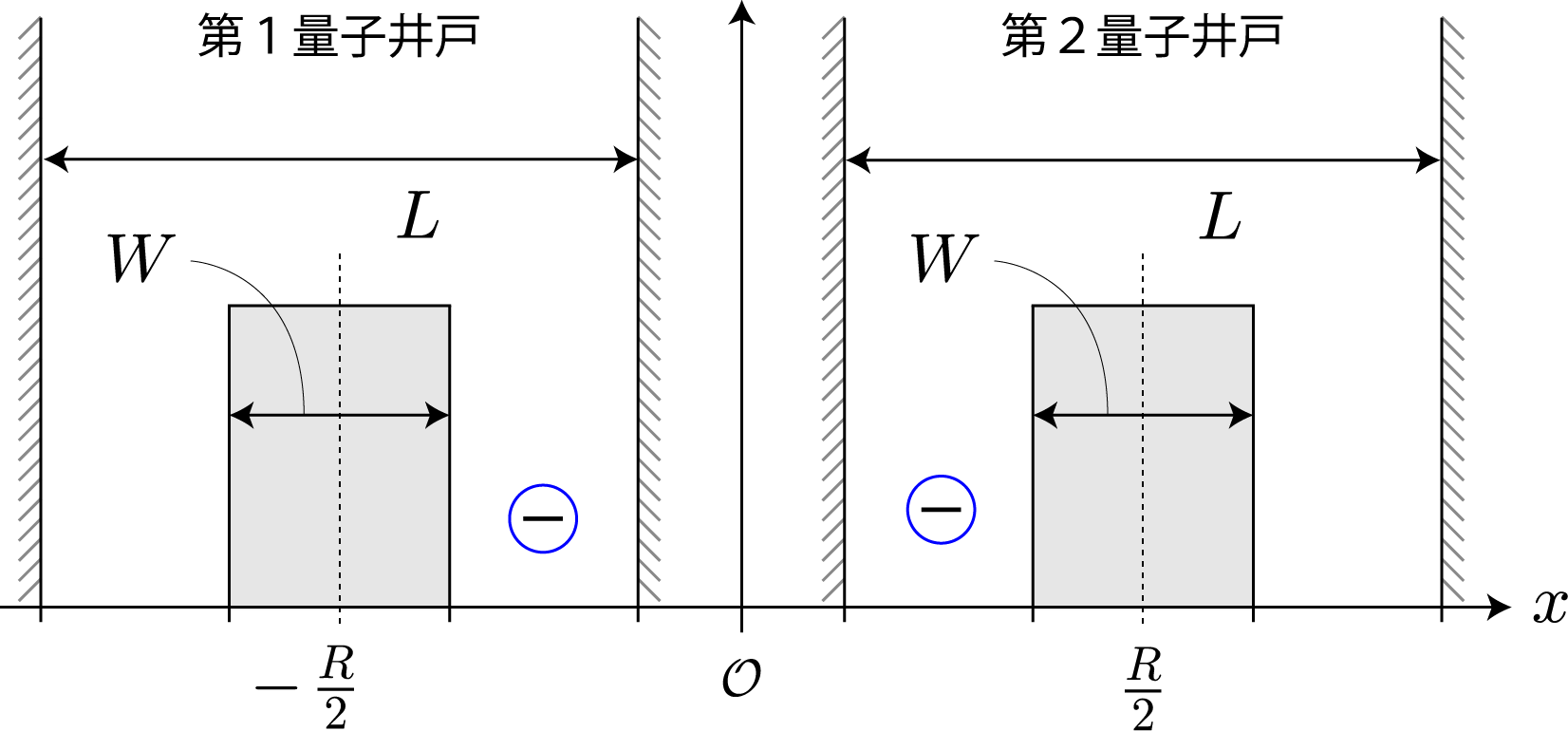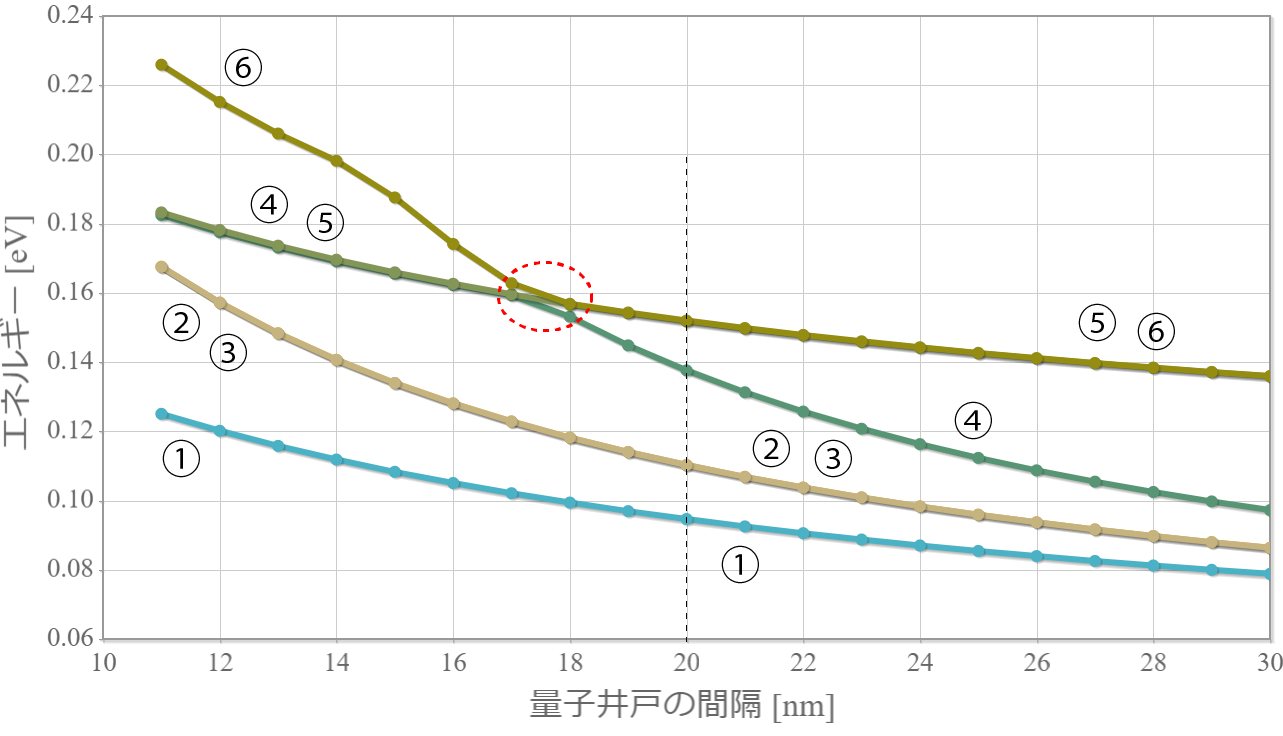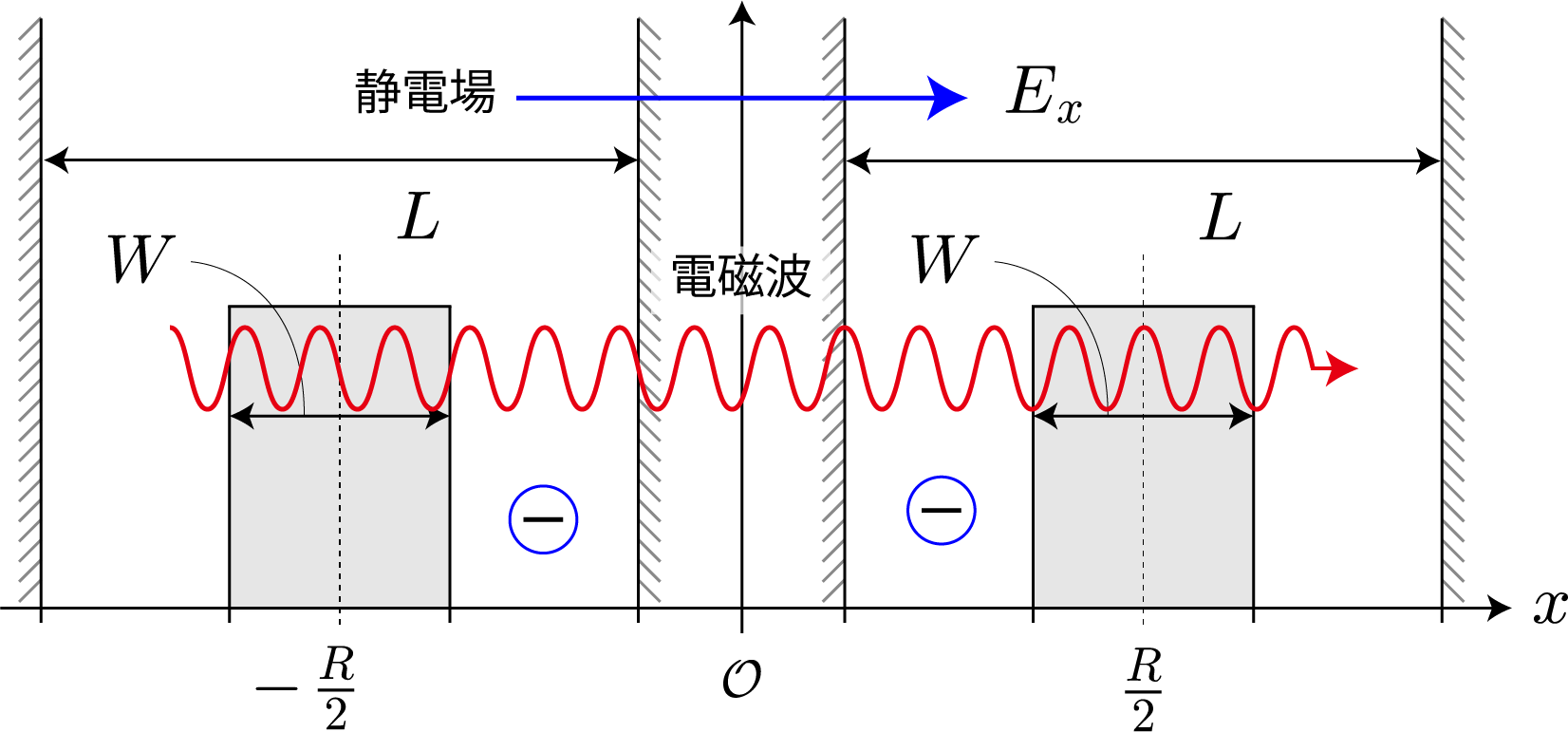
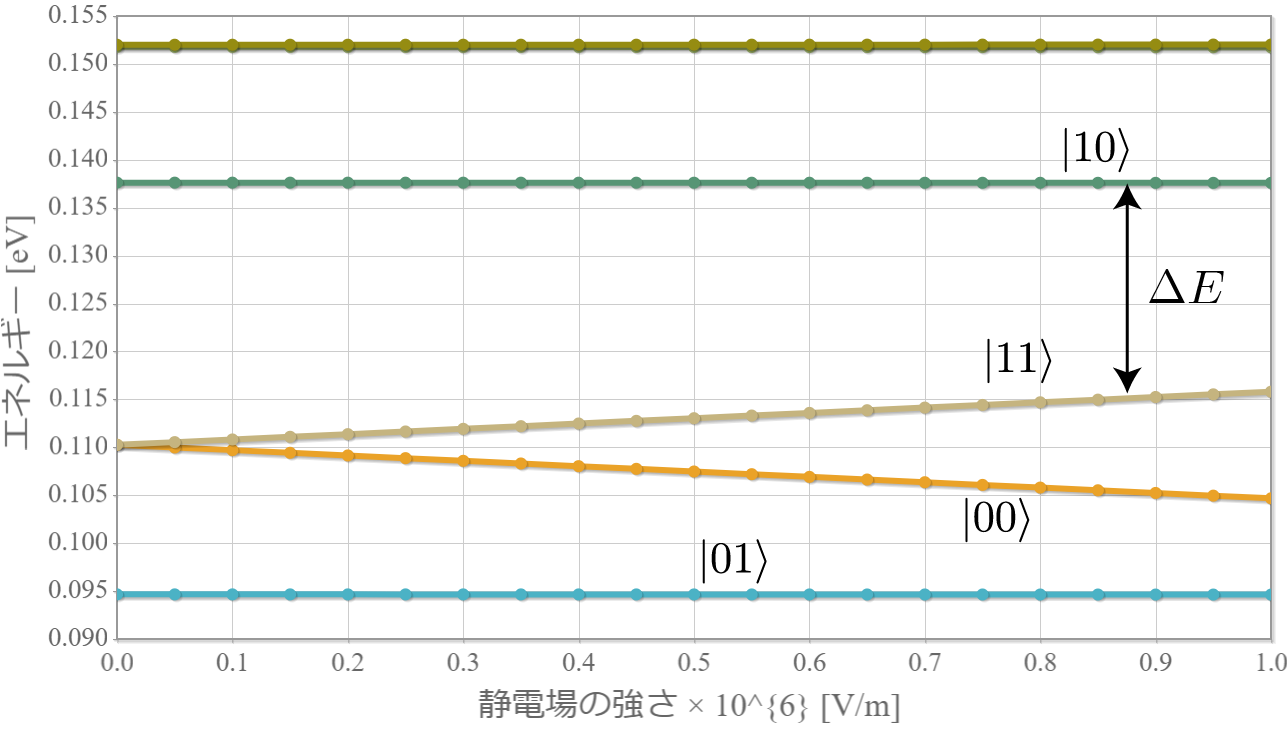
今回は、前回示したハミルトニアン(クーロン相互作用+静電場+電磁波)を用いて計算した結果を示すよ。上左図は前々回に示したエネルギー準位の静電場強度依存性だけれども、$|10\rangle$ と $|11\rangle$ のエネルギー差に対応した電磁波を入射して生じる状態遷移を計算するよ。ちなみにこれは、第1量子ビットが $|1\rangle$ のときに第2量子ビットを反転させる制御・NOT演算に対応しているよ。あとで示すけれども、2量子ビットのラビ振動は量子ビット同士が絡み合った量子もつれ(エンタングル)状態を任意に生成することができるよ。
遷移状態:$|10\rangle$ と $|11\rangle$ の存在確率の時間依存性
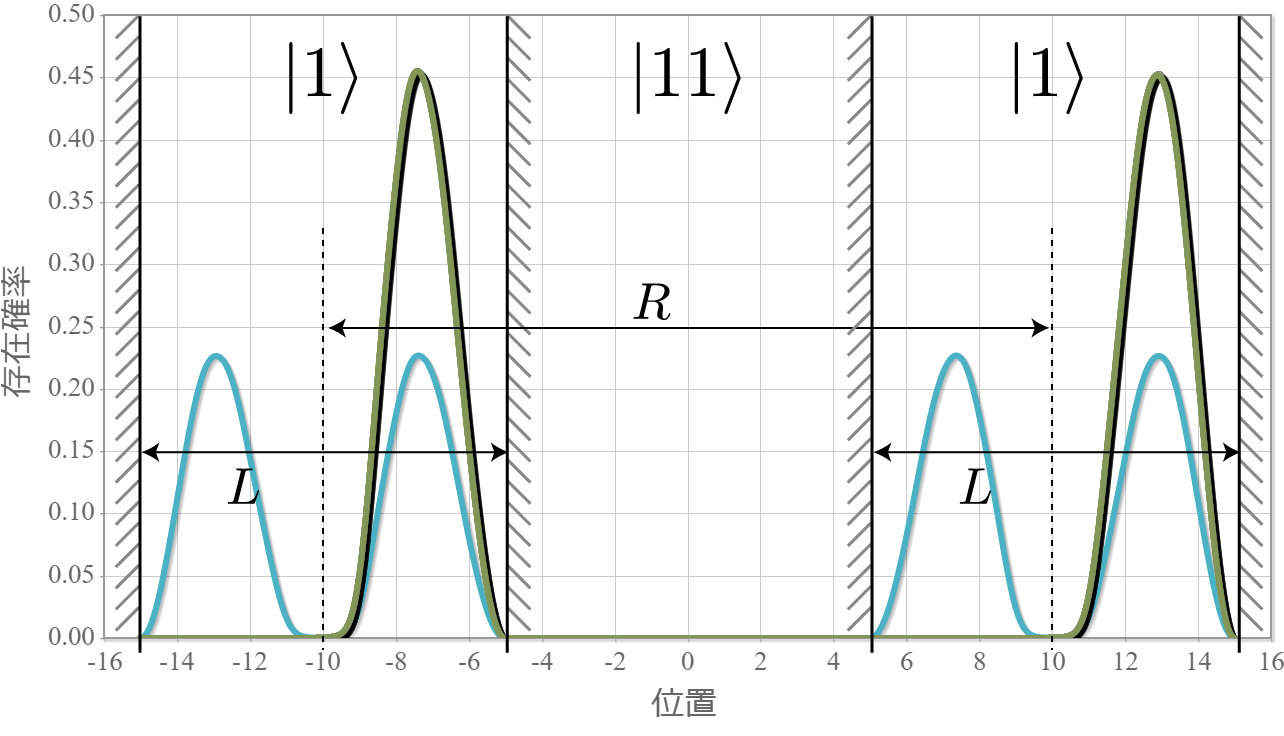
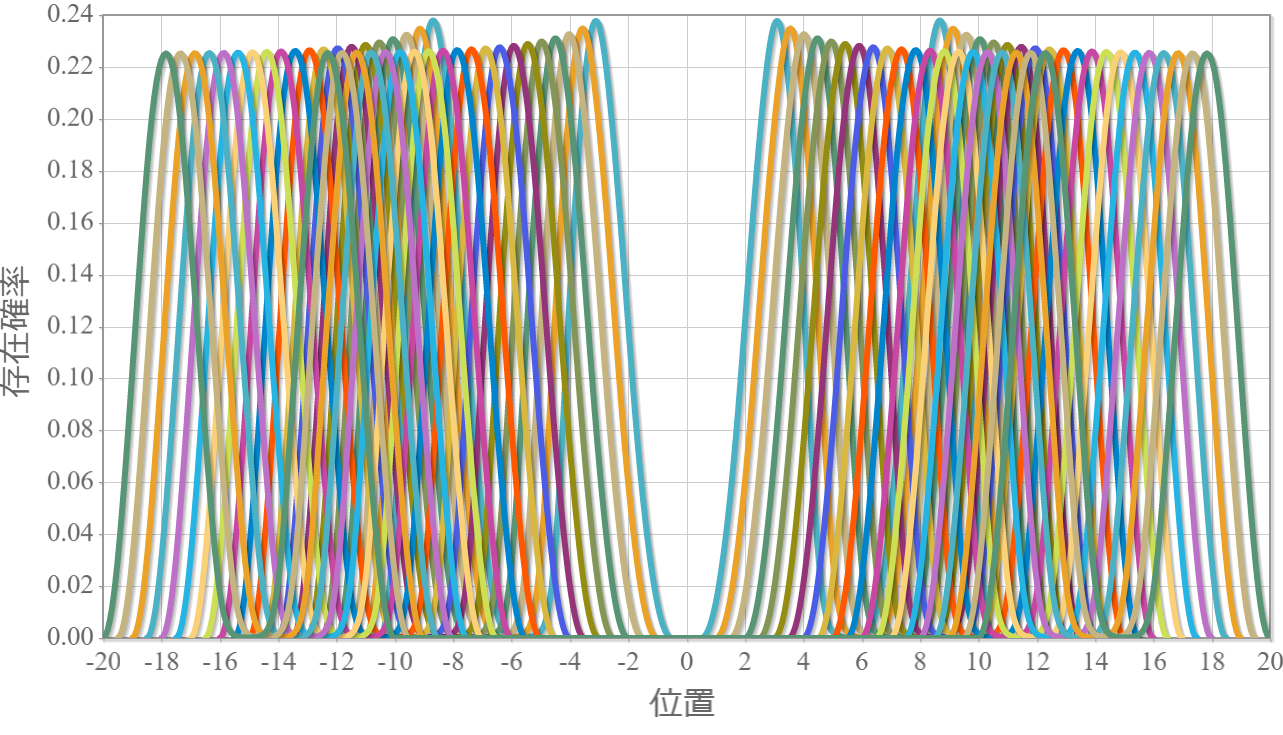
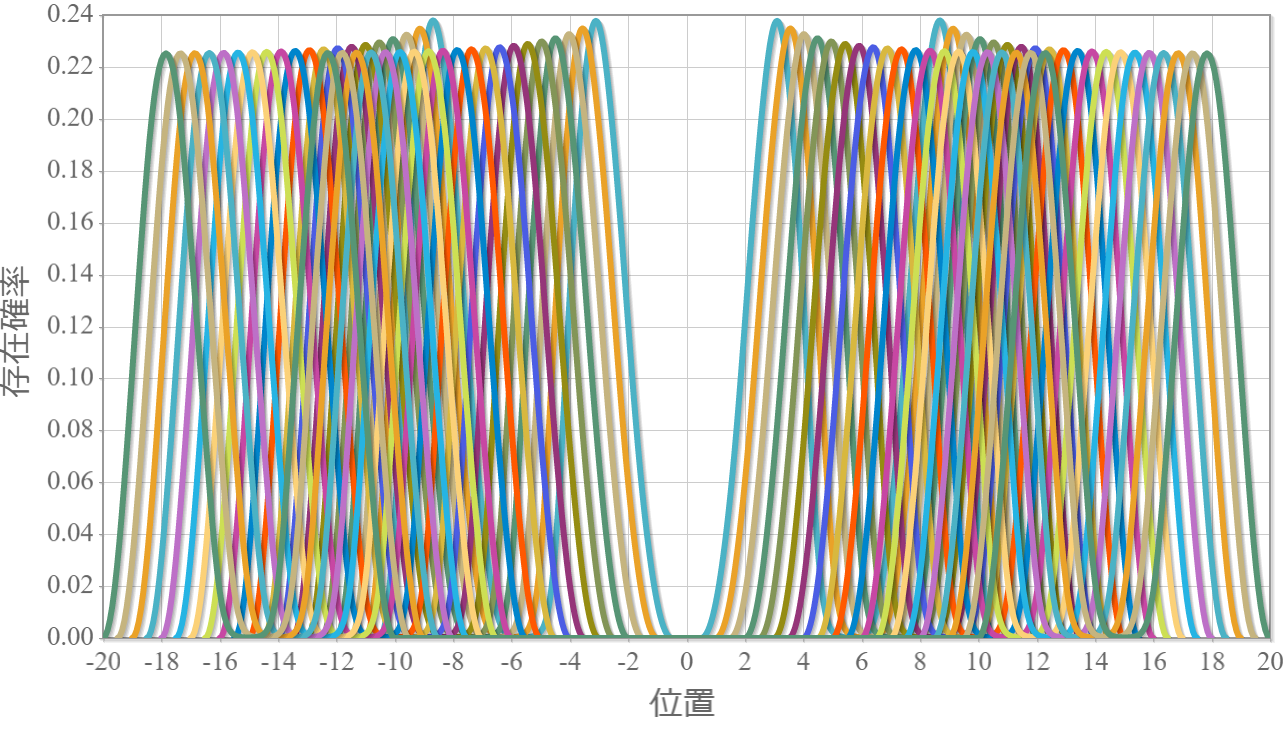
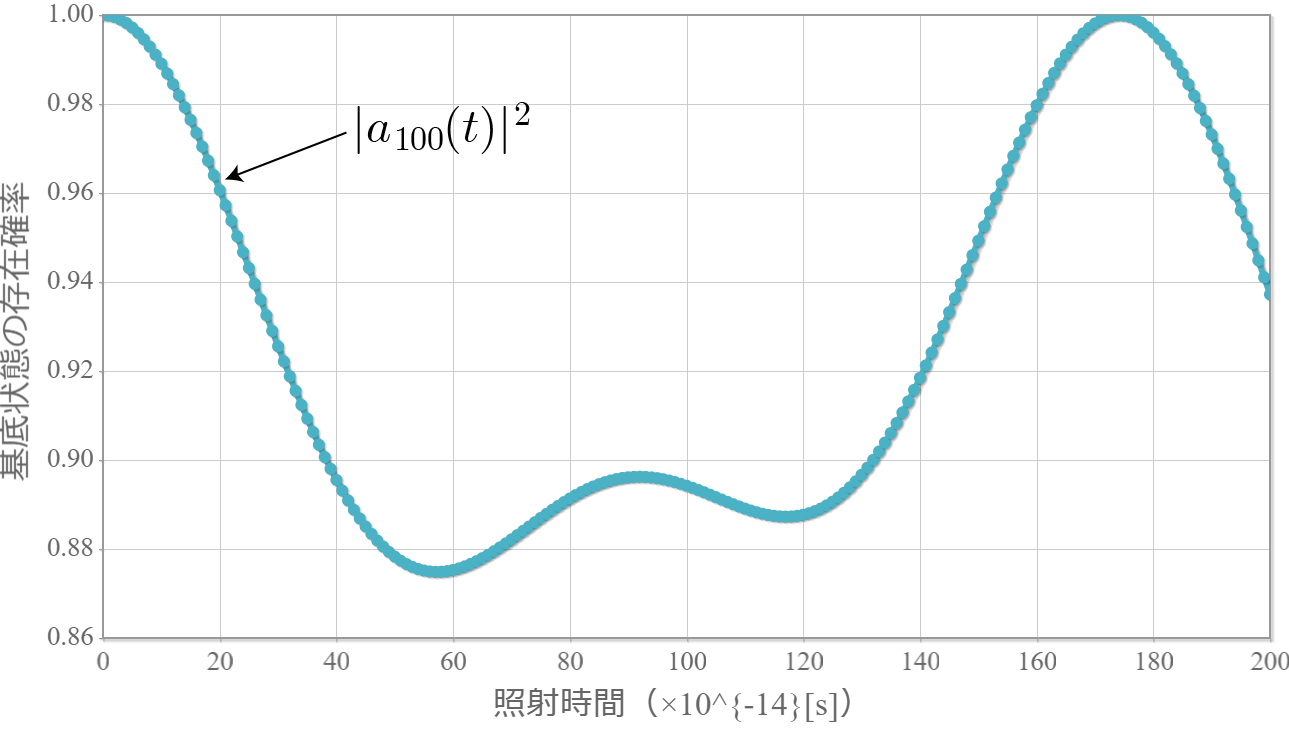
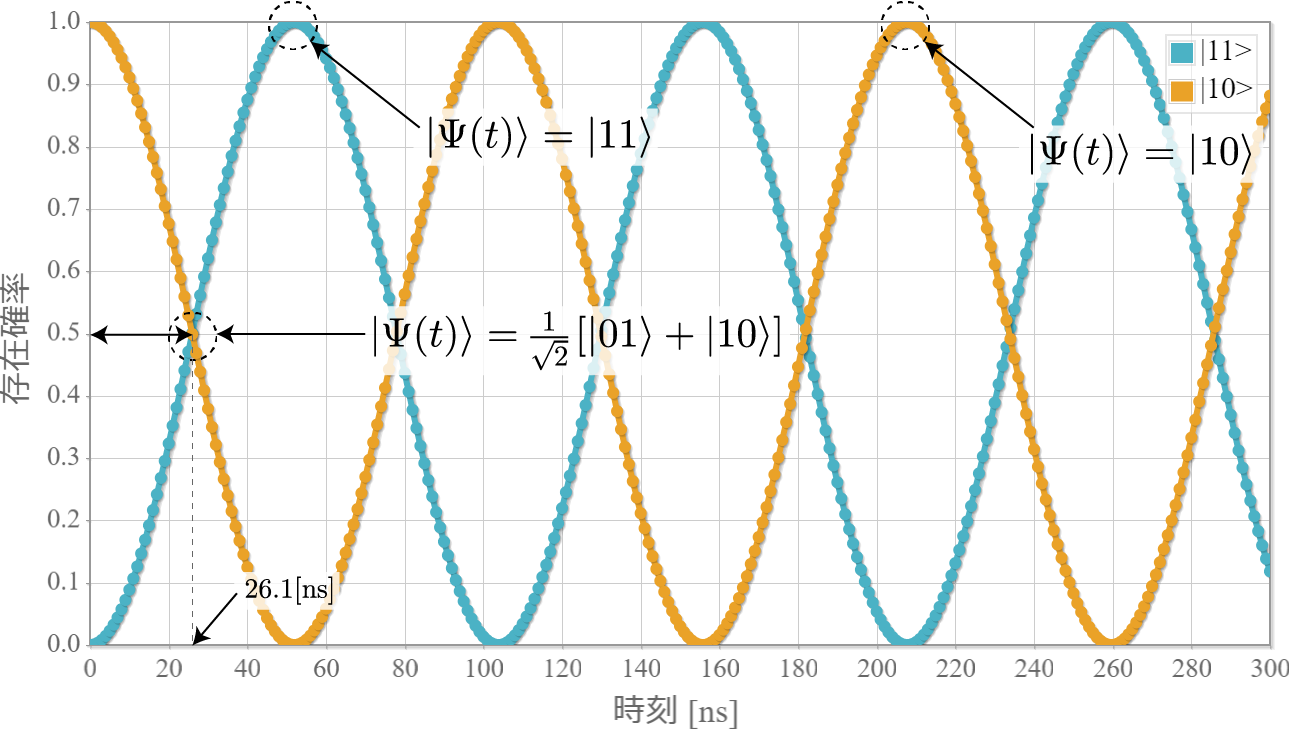
次のグラフは初期状態 $|10\rangle$ に角振動数 $\omega = \Delta E /\hbar$ の電磁波を入射したときの、$|11\rangle$ との状態遷移の様子だよ。ラビ振動の結果、2つの状態を三角関数的に行ったり来たりするね。$|10\rangle$ 100%の初期状態に約 $ 26.1[{\rm ns}]$ 照射すると、$|10\rangle$ と $|11\rangle$ の存在確率は50%つづとなり、さらに約 $ 26.1[{\rm ns}]$ 照射すると、反対に $|11\rangle$ 100% の状態になるね。ちょうど存在確率が反転する時間の光は「$\pi$パルス」って呼ばれるよ。
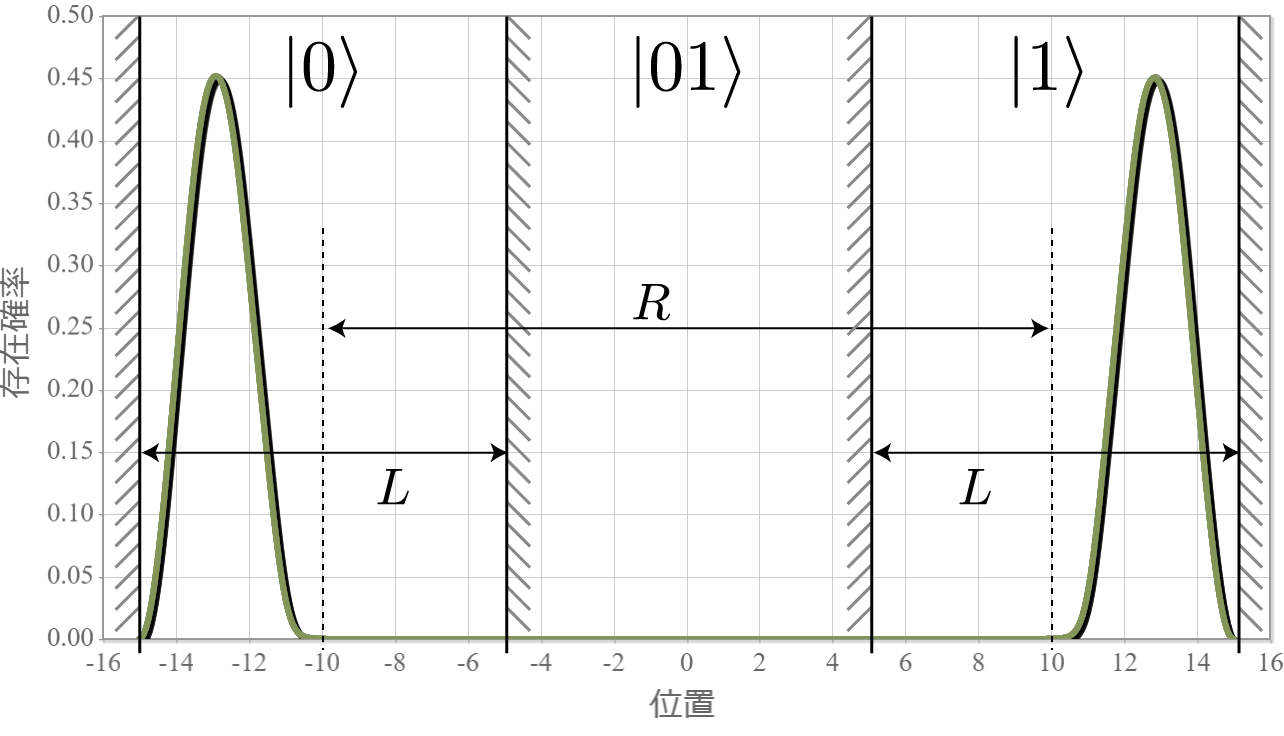
先にも言ったけれども、このラビ振動は2量子ビット同士が絡み合った量子もつれ状態を生み出すことができるね。例えば、$|10\rangle$ と基底状態の $|01\rangle$ のエネルギー差 $\Delta E_{01}^{11}$ として、角振動数 $\omega = \Delta E_{01}^{11} /\hbar$ の電磁波を $\pi$パルスの半分を入射すると、
\begin{align}
|\Psi(t)\rangle = \frac{1}{\sqrt{2}} \left[ |10\rangle + |01\rangle \right]
\end{align}
という状態を作ることができるね。これは単に $|10\rangle$ と $|01\rangle $ の存在確率が 50%づつっていうだけでなくて、第1量子ビットを観測したときに、第2量子を観測しなくてもその状態が100%の確率で分かるという量子もつれ状態となっているよ。具体的には、第1量子ビットが $|0\rangle$ の場合には第2量子ビットは必ず $|1\rangle$ に存在し、また反対に第1量子ビットが $|1\rangle$ の場合には第2量子ビットは必ず $|0\rangle$ に存在するよ。ちなみに、この量子井戸の間隔を量子状態が変化しないようにゆっくりと、どこまで離していっても成り立つよ。そのため、通信に利用することができると考えられているよ。その場合は、量子井戸による量子もつれではなく、光子をを用いた量子もつれを利用するよ。
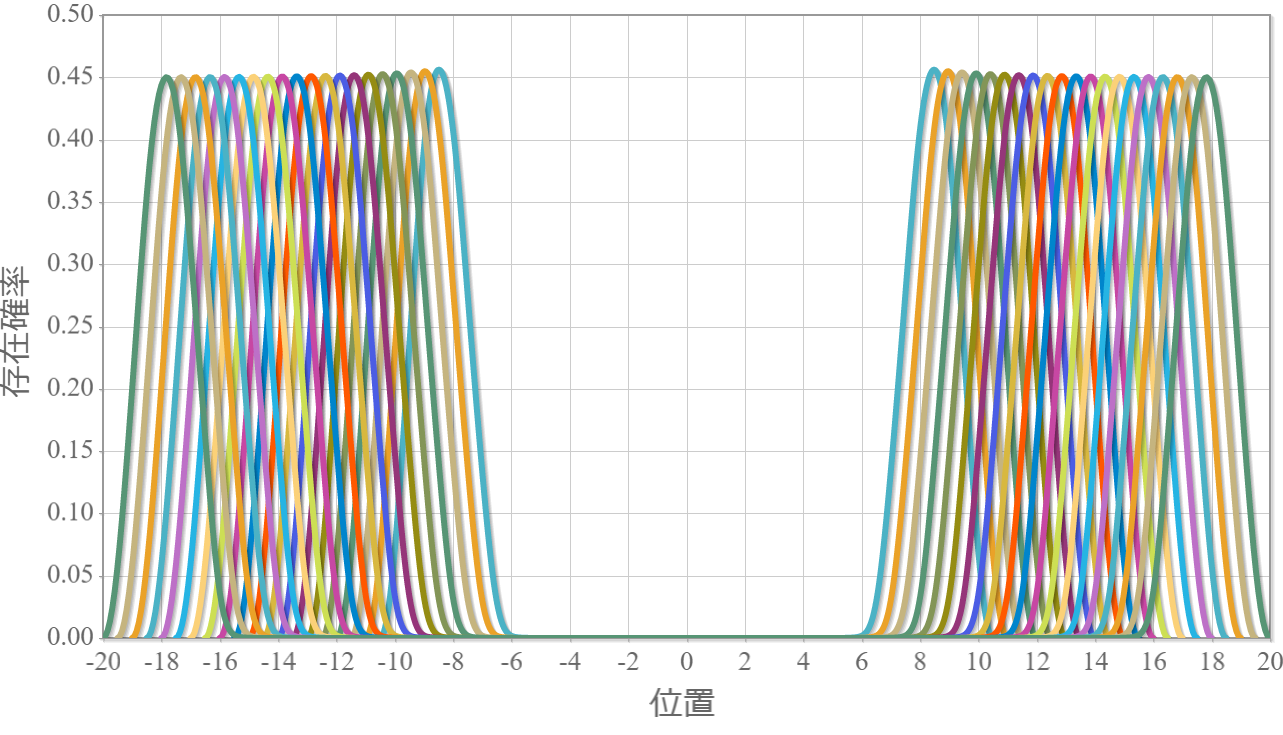
制御NOT演算に対応する波動関数の時間発展
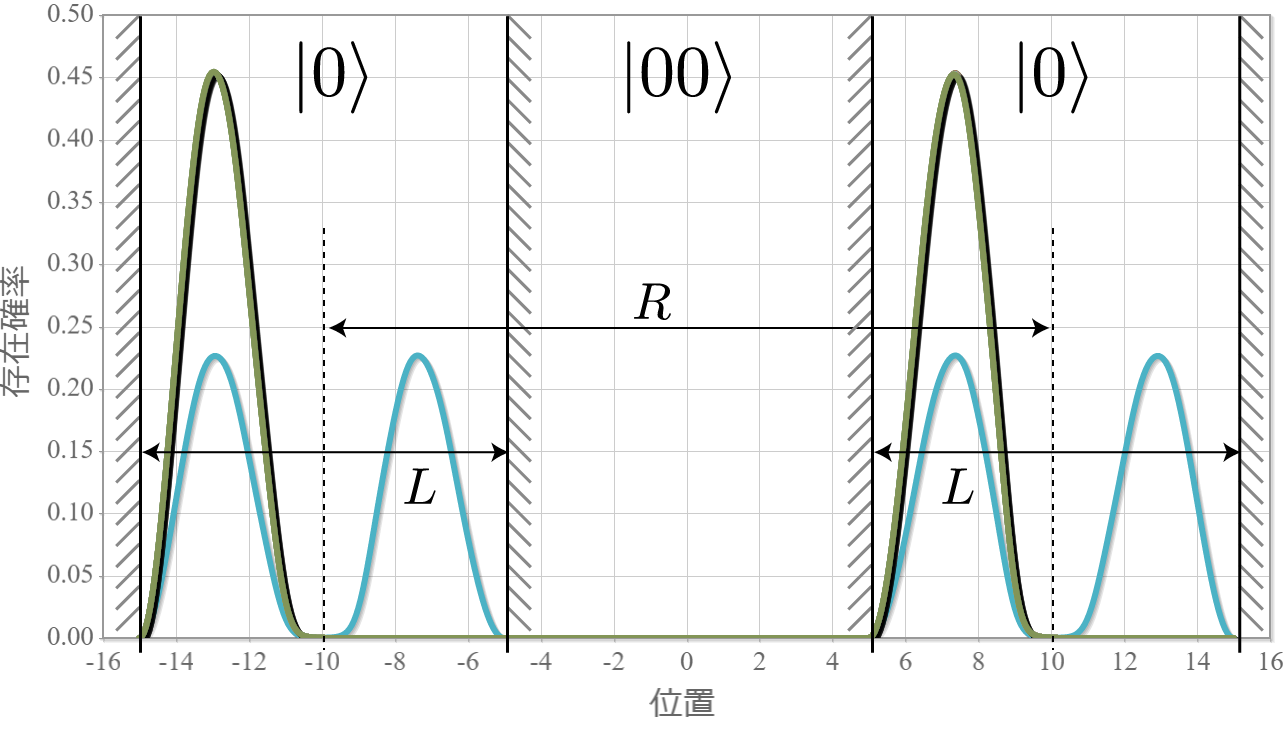
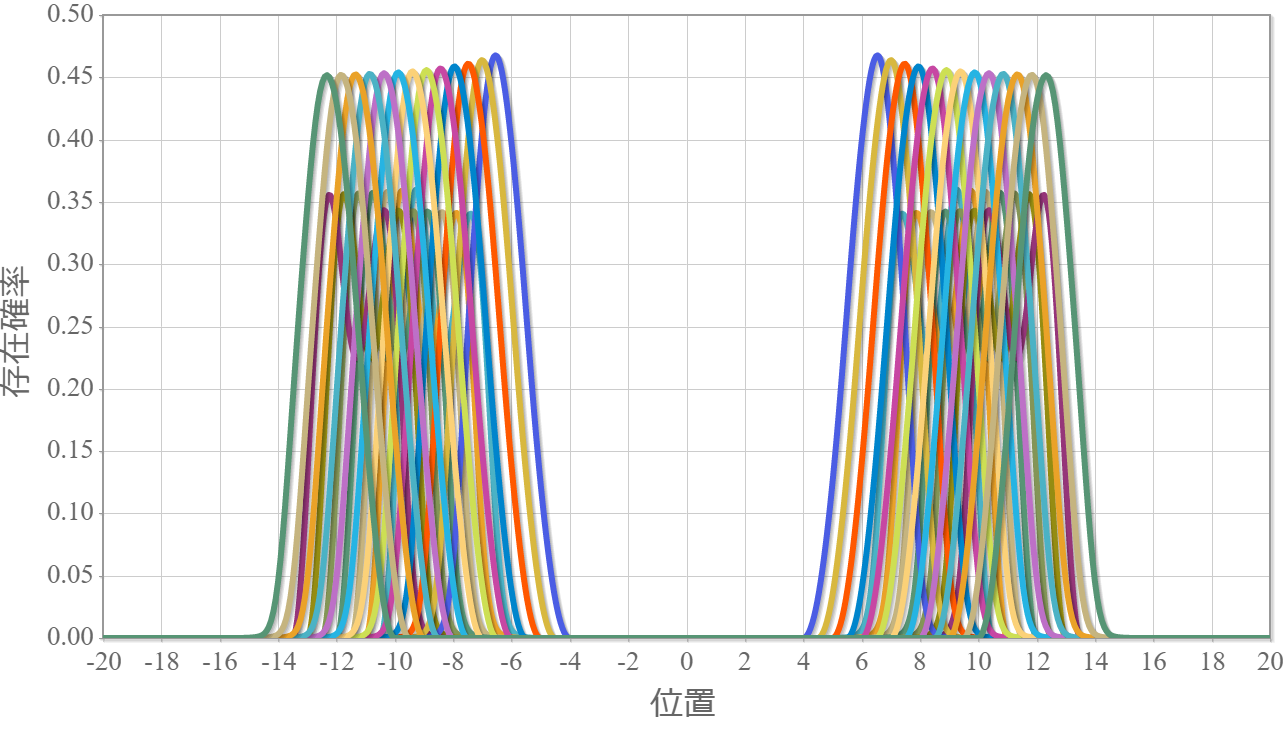
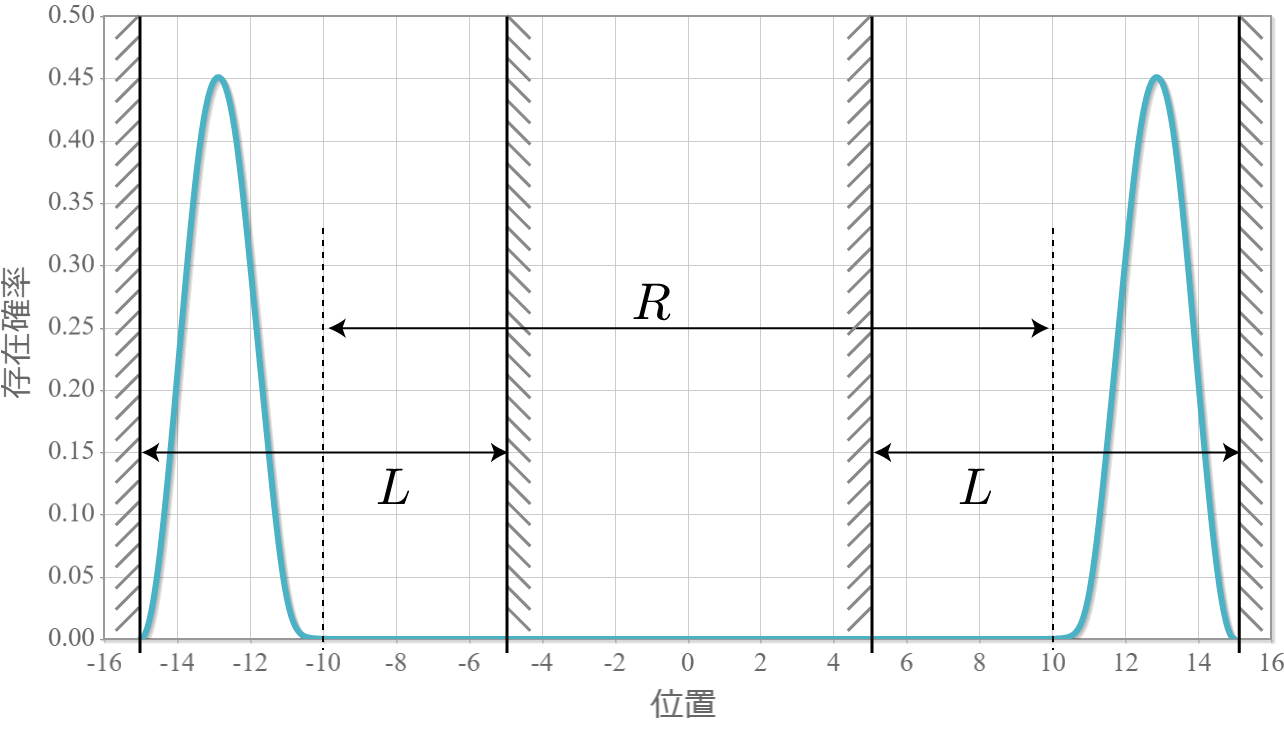
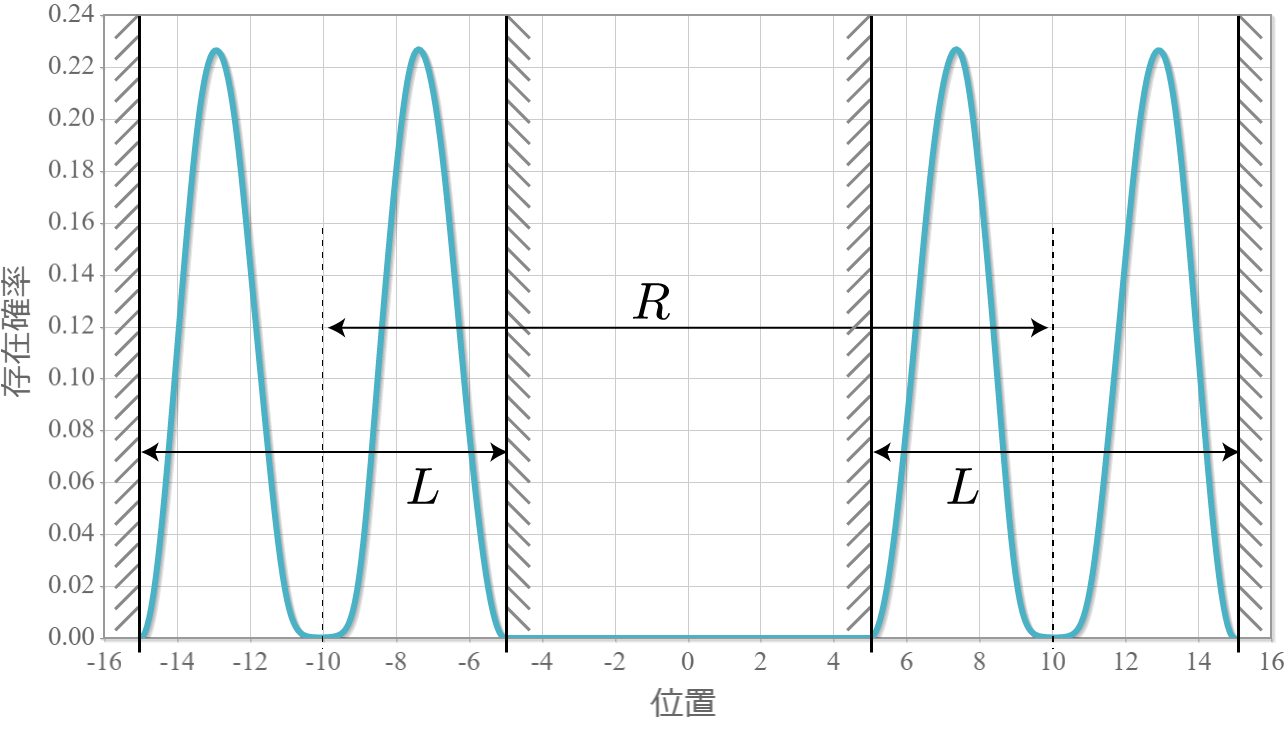
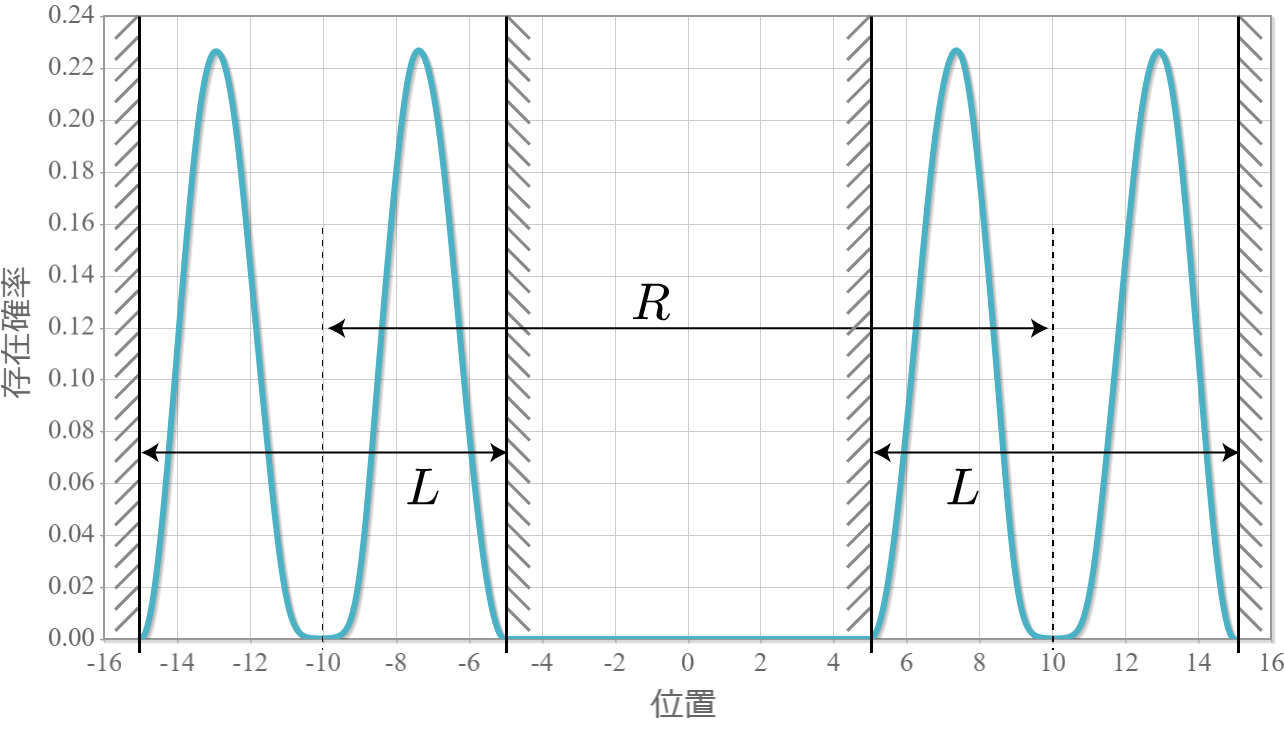
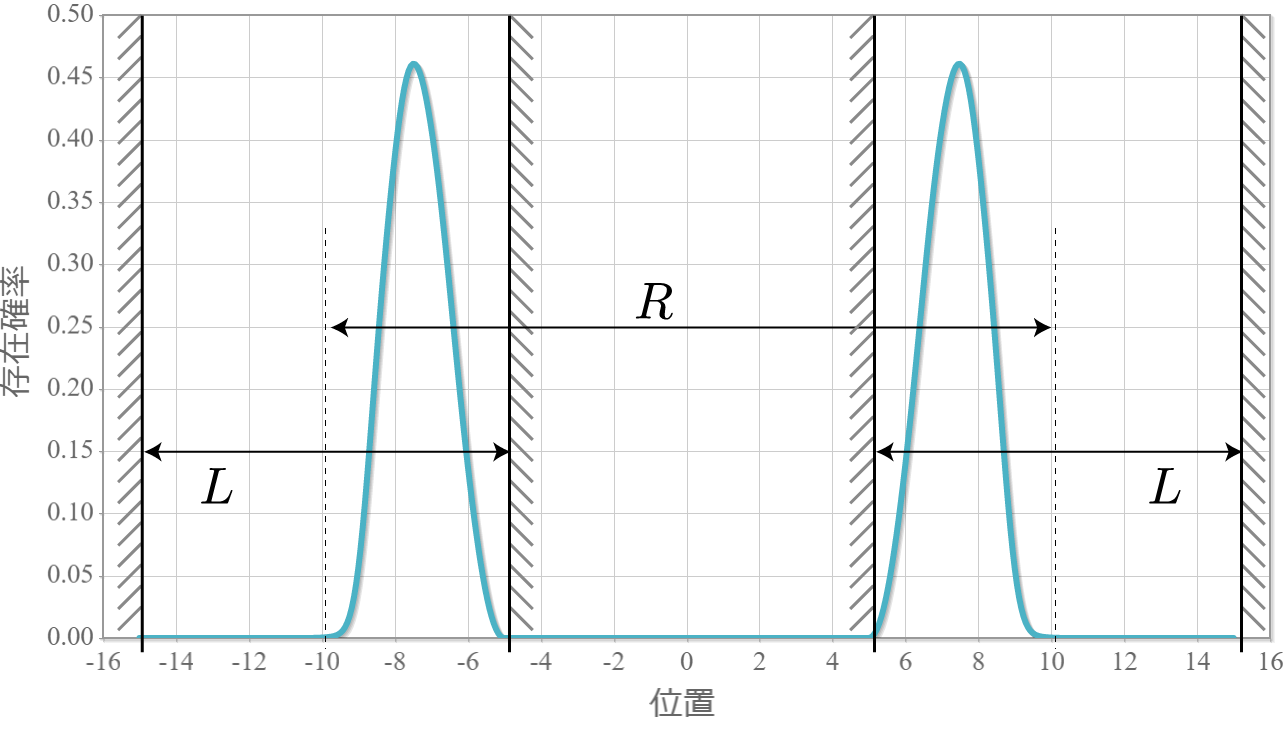
次の図はラビ振動による制御NOT演算時の波動関数の時間経過を示したアニメーションだよ。左の第1量子井戸は電子が右側( $|1\rangle$ )、第2量子井戸は電子が左側( $|0\rangle$ )と右側( $|1\rangle$ )を行ったり来たりしているね。
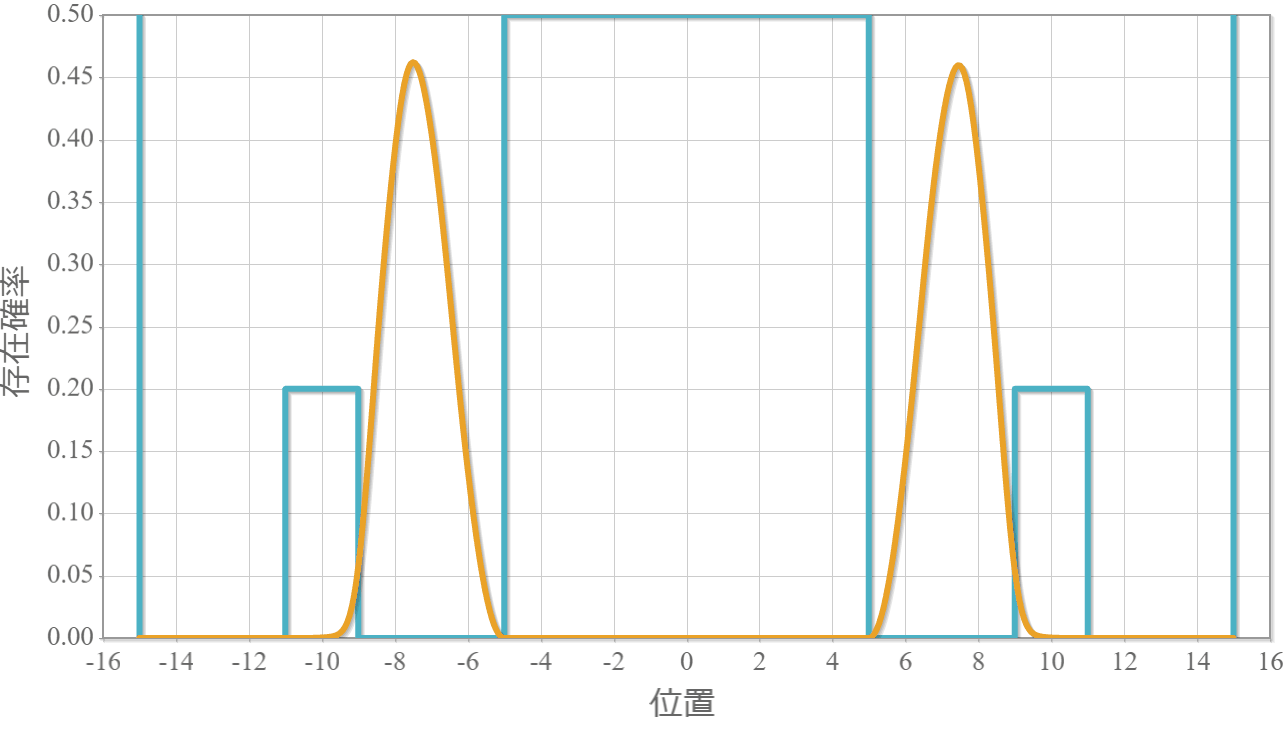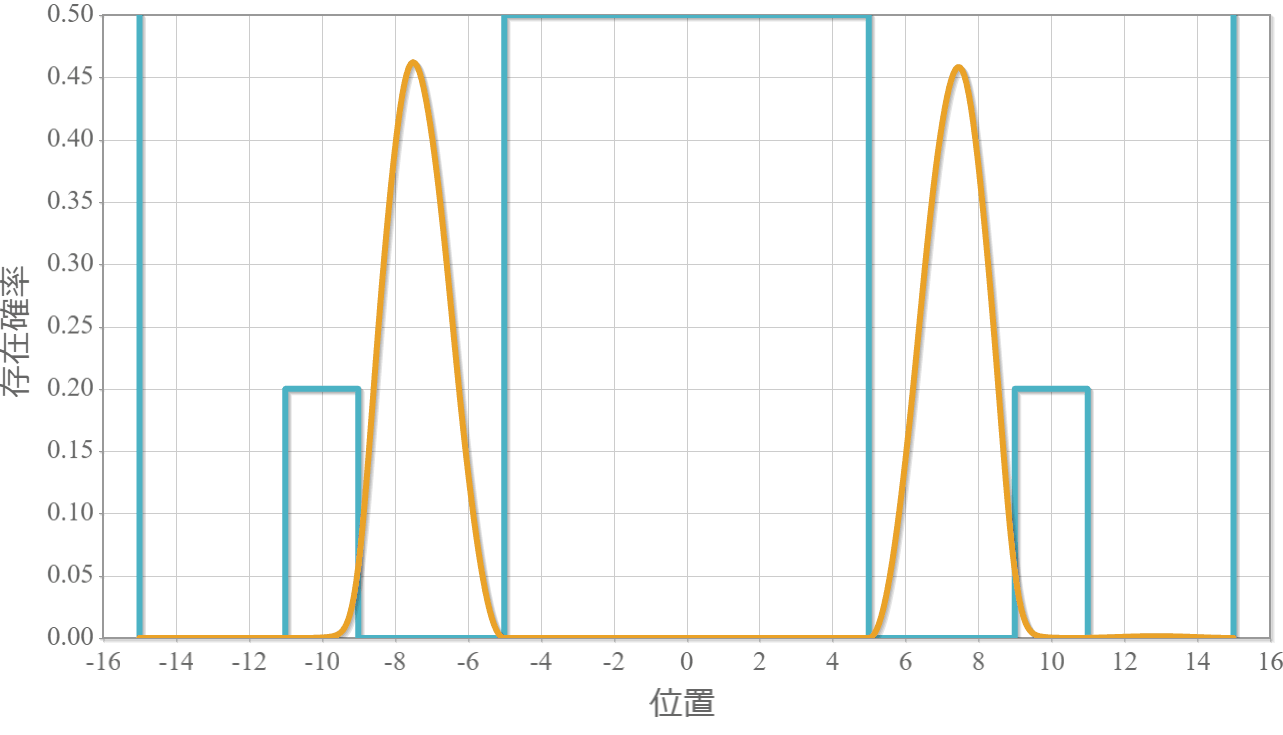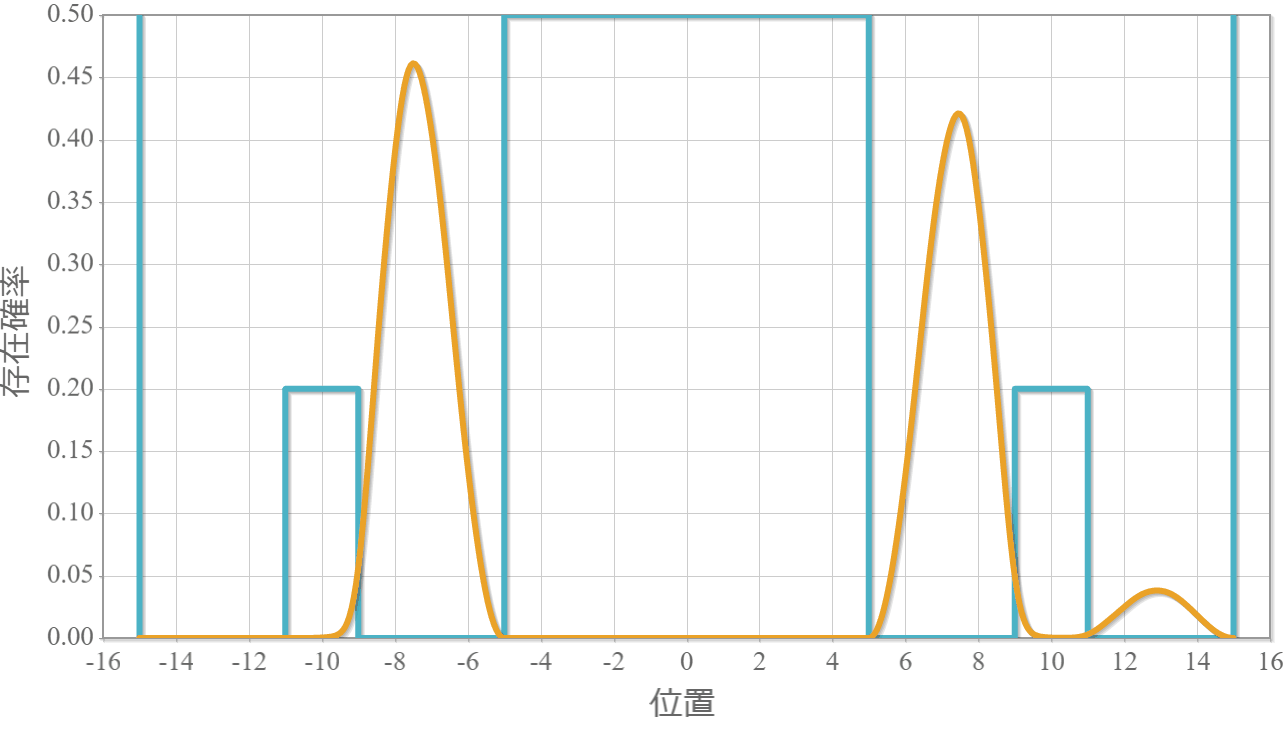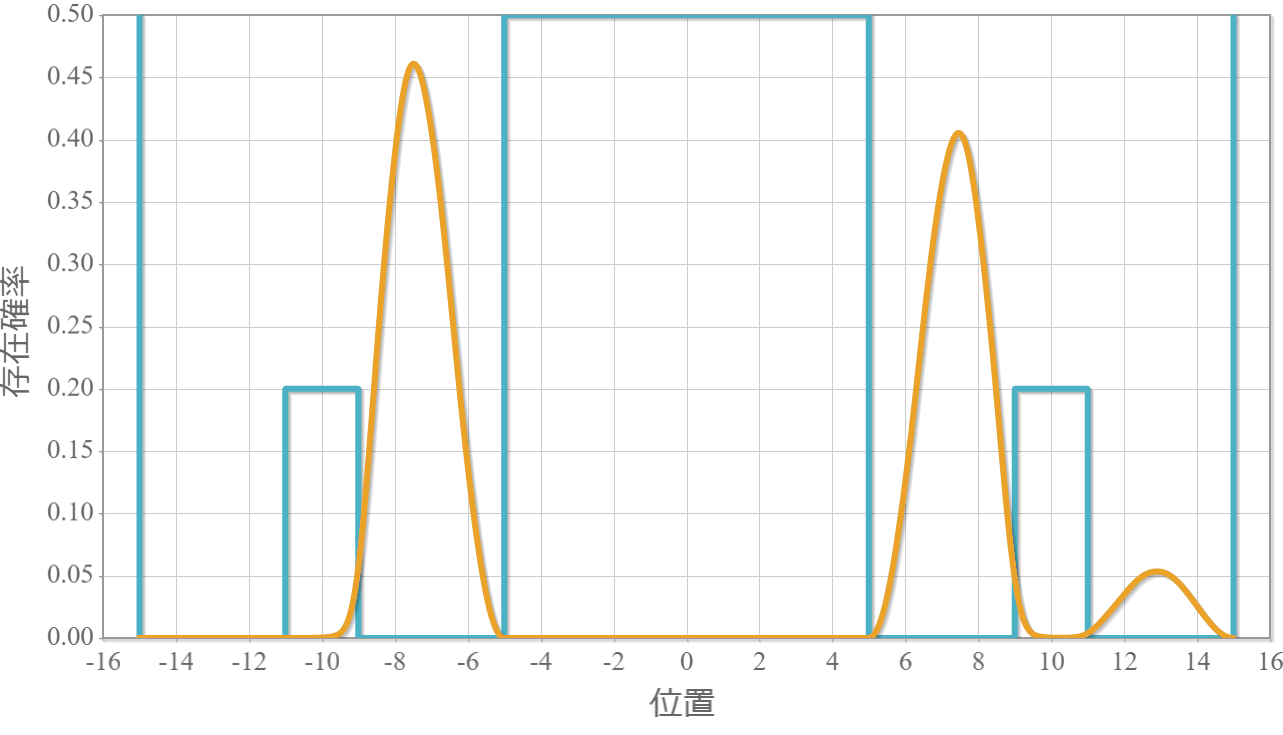
これで量子コンピュータの2量子ビットマシンの動作原理シミュレーションは完成したよ。