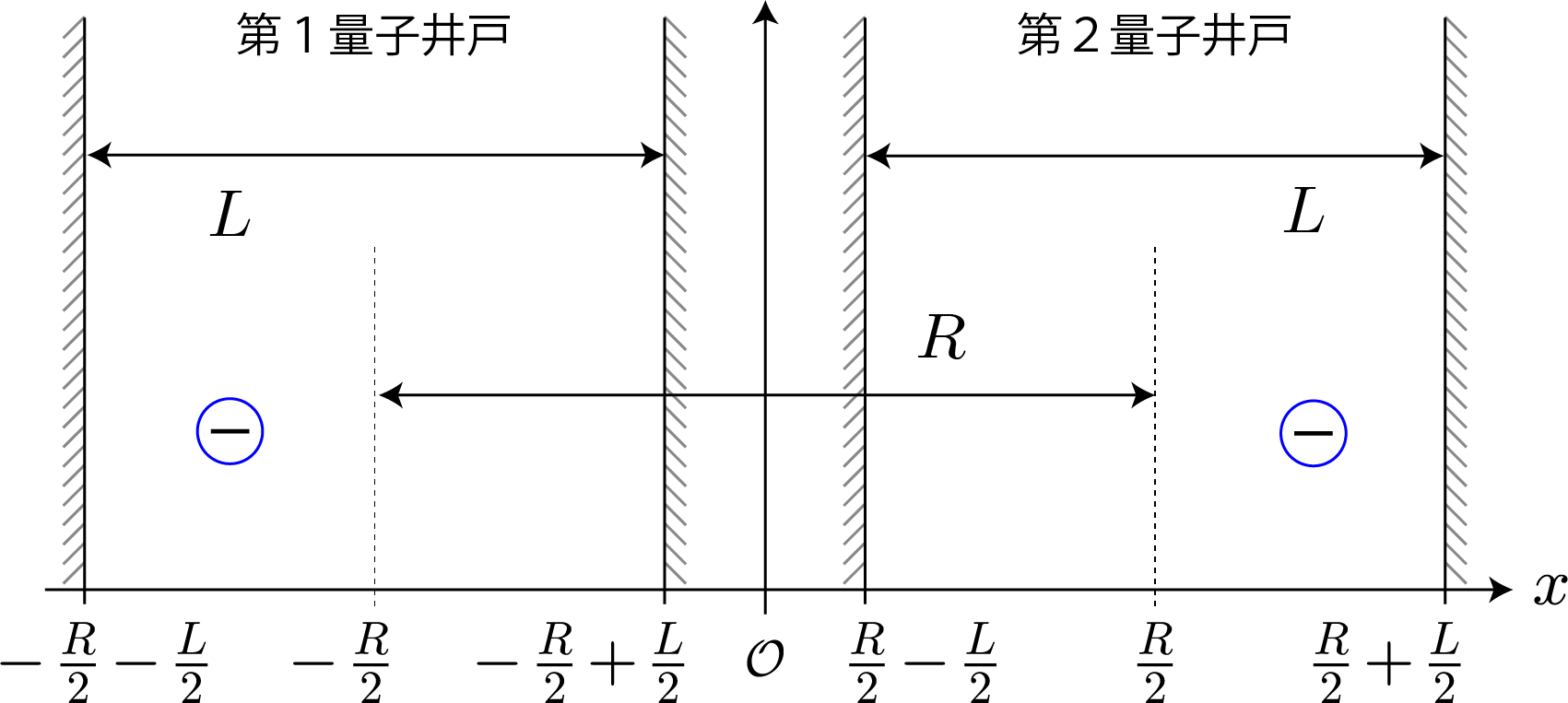
本稿では、2量子ビットの量子ゲートを作るための基礎実験として、右図のような2つの量子井戸に束縛された2個の電子の固有状態を計算するよ。電子が入れ替わらない場合、2電子の波動関数はそれぞれの量子井戸内の固有状態の積で表すことができるね。つまり、それぞれの量子井戸の固有関数を計算するための正規直交系を
\begin{align}
\varphi_{n_1}(x_1) &\ = \sqrt{\frac{2}{L}}\sin\left[ k_{n_1} \left( x_1 + \frac{R}{2} + \frac{L}{2}\right)\right] \ , \
k_{n_1} = \frac{\pi(n_1+1)}{L} \\
\varphi_{n_2}(x_2) &\ = \sqrt{\frac{2}{L}}\sin\left[ k_{n_2} \left( x_2 – \frac{R}{2} + \frac{L}{2}\right)\right] \ , \
k_{n_2} = \frac{\pi(n_2+1)}{L} \\
\end{align}
と表した場合、2電子状態の固有関数は、先の正規直交系の積
\begin{align}
\varphi_{n_1n_2}(x_1, x_2) = \varphi_{n_1}(x_1)\varphi_{n_2}(x_2)
\end{align}
を用いて次のように展開することができるね。
\begin{align}
\psi(x_1, x_2) = \sum\limits_{n_1n_2} a_{n_1n_2} \varphi_{n_1n_2}(x_1, x_2)
\end{align}
これまでと同様、この系に対するハミルトニアンは
\begin{align}
\hat{H} = -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_1^2} -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_2^2} + \frac{e^2}{4\pi\epsilon_0}\,\frac{1}{|x_1-x_2|} \equiv \hat{H}^{(0)}_1 + \hat{H}^{(0)}_2 +\hat{V}_{12}
\end{align}
なので、シュレーディンガー方程式
\begin{align}
\hat{H}\psi(x_1, x_2) = E \psi(x_1, x_2)
\end{align}
に代入して、$\varphi_{m_1m_2}^*(x_1, x_2)$ を両辺に掛けて全空間で積分すると
\begin{align}
(E^{(0)}_{m_1} + E^{(0)}_{m_2})a_{m_1m_2} + \sum\limits_{n_1n_2} a_{n_1n_2} \langle m_1,m_2| \hat{V}_{12} | n_1, n_2\rangle = E a_{m_1m_2}
\end{align}
と、いつもどおり固有値方程式が得られるね。ただし、
\begin{align}
E^{(0)}_{m_1} = \frac{\hbar^2k^2_{m_1}}{2m_e} \ &\ , \ E^{(0)}_{m_2} = \frac{\hbar^2k^2_{m_2}}{2m_e} \\
\langle m_1,m_2| \hat{V}_{12} | n_1, n_2\rangle &\ \equiv \int_{-\frac{R}{2}-\frac{L}{2}}^{-\frac{R}{2}+\frac{L}{2}} dx_1\int_{\frac{R}{2}-\frac{L}{2}}^{\frac{R}{2}+\frac{L}{2}} dx_2 \varphi_{m_1m_2}^*(x_1, x_2) V_{12} \varphi_{n_1n_2}(x_1, x_2)
\end{align}
だよ。この固有値方程式を解いて得られた固有ベクトルがそのまま先の展開係数 $a_{n_1n_2}$ となるね。最後に波動関数から得られる電子の存在確率は次のとおりだよ。
\begin{align}
\rho(x) = \left\{ \matrix{ 0 & x <-\frac{R}{2} - \frac{L}{2} \cr \int_{\frac{R}{2}-\frac{L}{2}}^{\frac{R}{2}+\frac{L}{2}} |\psi(x, x_2)|^2 dx_2 & -\frac{R}{2} - \frac{L}{2} \le x \le -\frac{R}{2} + \frac{L}{2} \cr 0 & -\frac{R}{2} + \frac{L}{2} < x < \frac{R}{2} - \frac{L}{2} \cr \int_{-\frac{R}{2}-\frac{L}{2}}^{-\frac{R}{2}+\frac{L}{2}} |\psi(x_1, x)|^2 dx_1 & \frac{R}{2} - \frac{L}{2} \le x \le \frac{R}{2} + \frac{L}{2} \cr 0 & \frac{R}{2} + \frac{L}{2} < x} \right.
\end{align}
計算結果:2つの量子井戸の間隔依存性
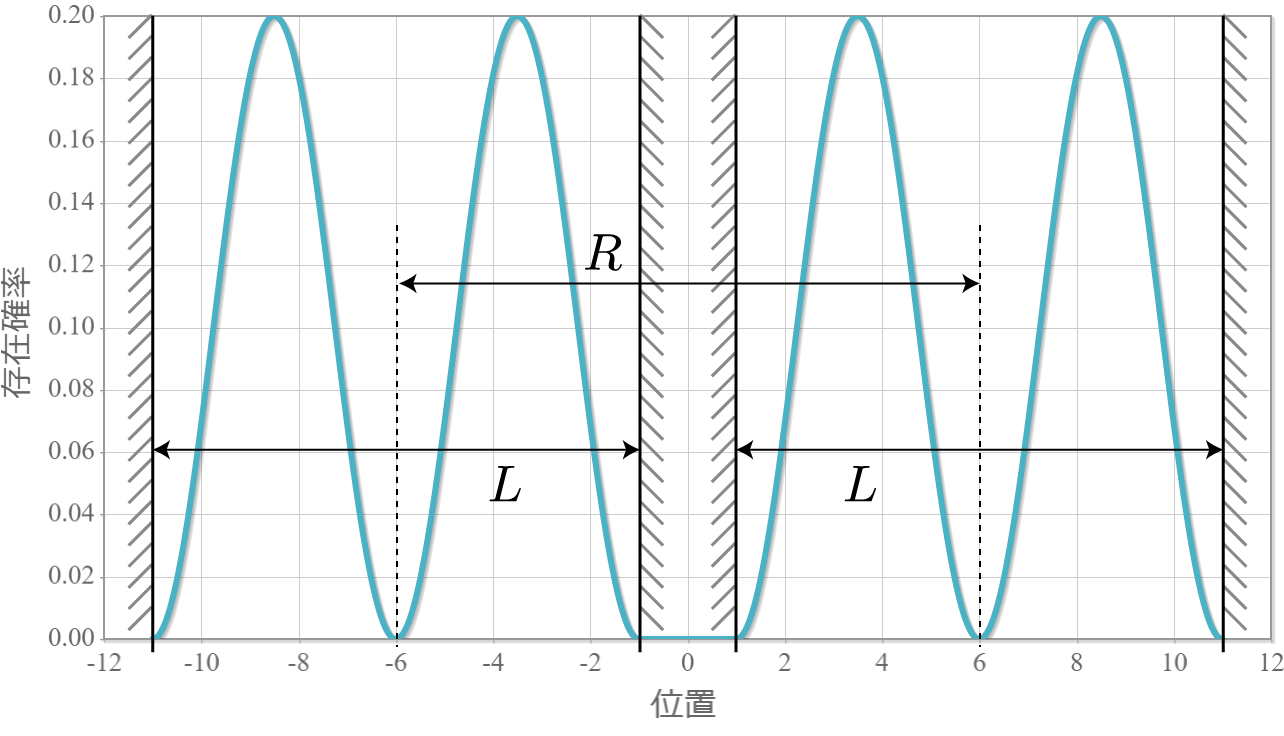
まずリファレンスとして、クーロン相互作用が存在しない場合を示しておくよ。次の4つの図は量子井戸の幅 $L=10.0\times10^{-9} [{\rm m}]= 10[{\rm nm}]$、量子井戸の間隔 $R = 12[{\rm nm}]$ とした場合の基底状態から第3励起状態までの電子存在確率の空間分布だよ。独立した2つの量子井戸内の電子が想定通りに空間分布していることが確認できるね。ちなみに第1励起状態と第2励起状態はこの場合、エネルギー固有値は同じなので縮退しているよ。
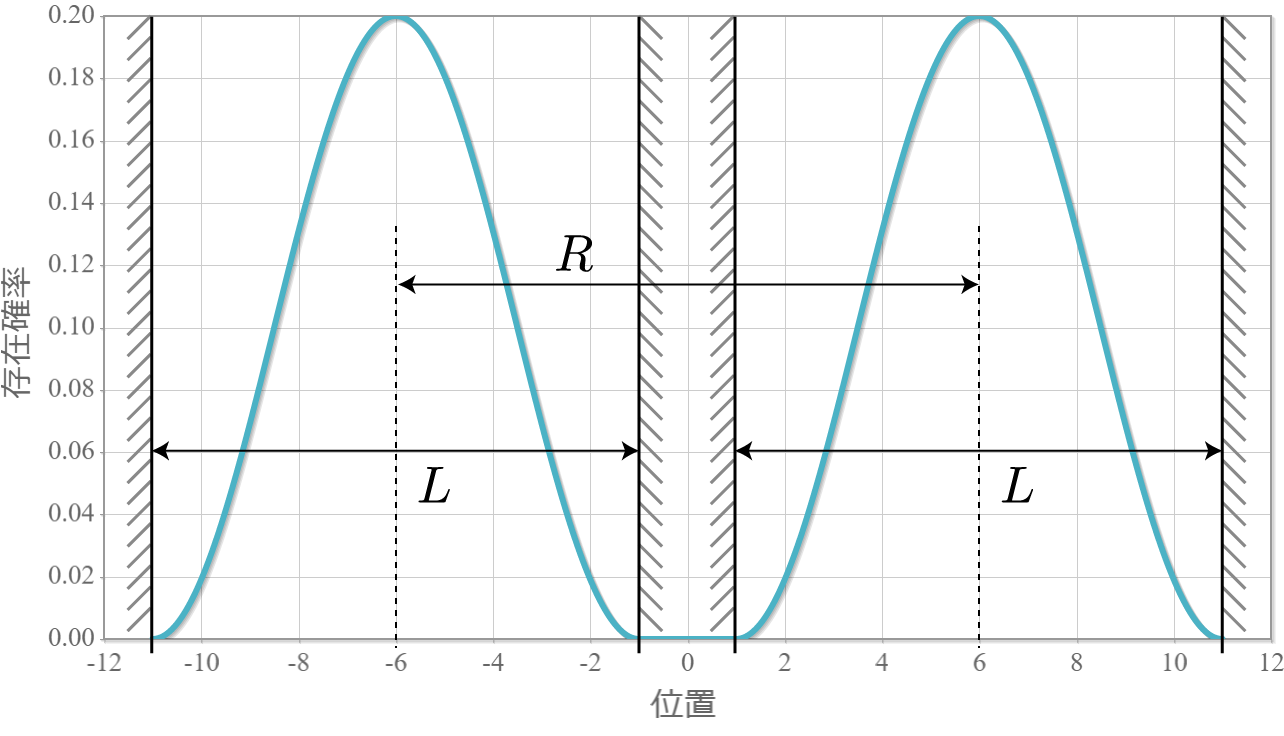
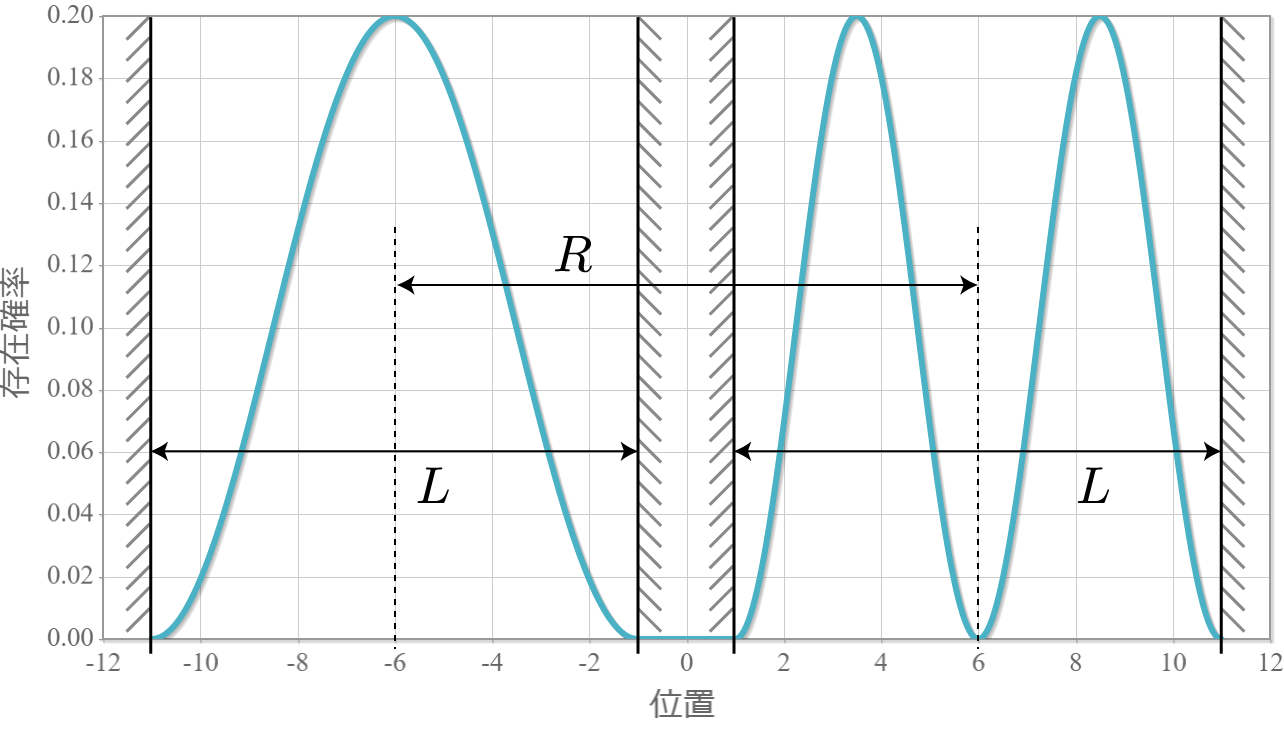
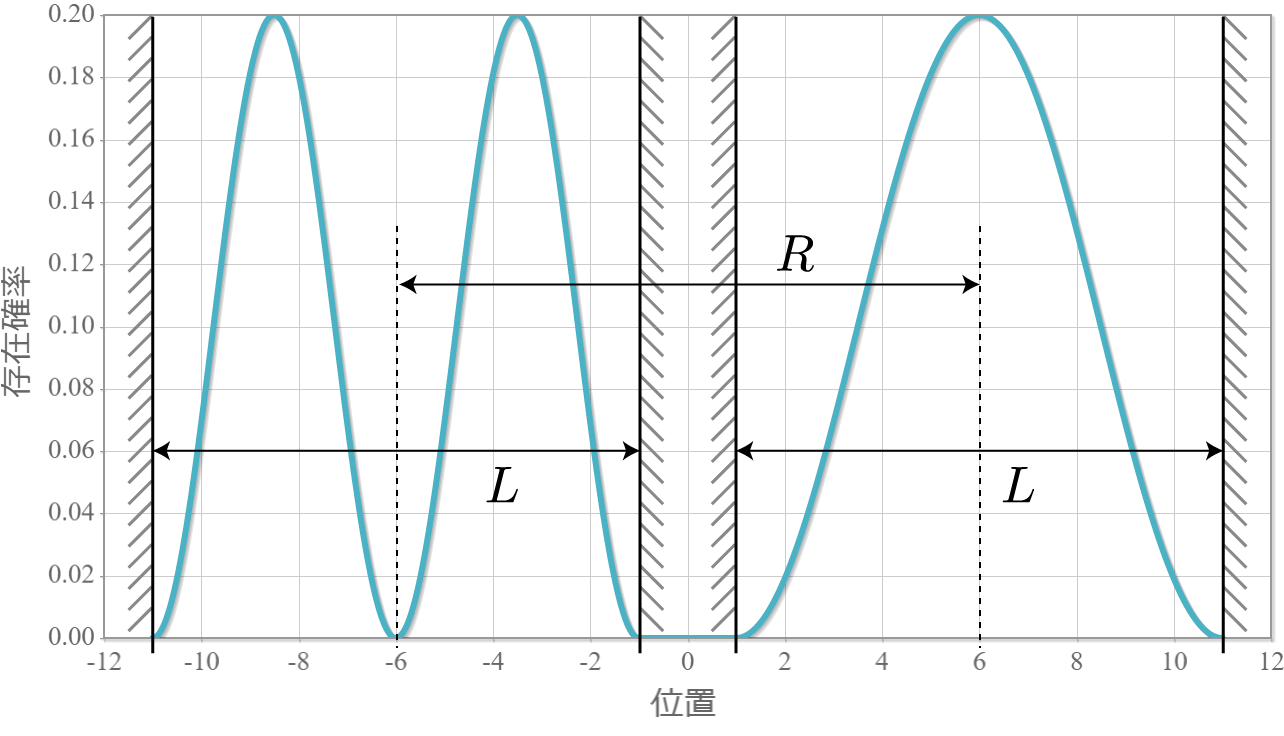
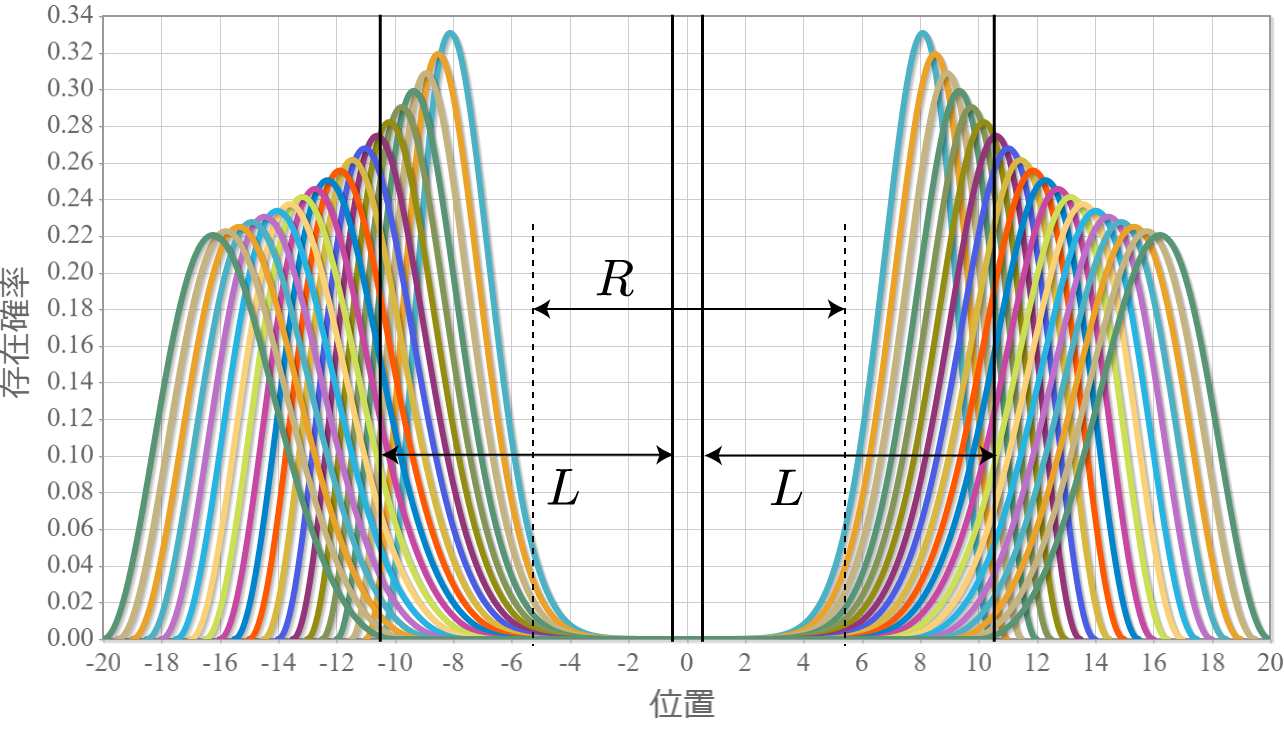
続いて、先の電子間にクーロン相互作用が存在する場合の空間分布を示すよ。次の4つの図は量子井戸の幅 $L=10.0\times10^{-9} [{\rm m}]= 10[{\rm nm}]$ に固定して、2つの量子井戸の間隔を $R = 11[{\rm nm}]$ から $ 30 [{\rm nm}]$ まで $ 1 [{\rm nm}]$ づつ広げていったときの基底状態から第3励起状態までの電子存在確率の空間分布だよ。クーロン相互作用で電子は反発するので、電子分布は原点で空間対称となるね。間隔が狭いほど相互作用が無い場合と比較して量子井戸の右側だけとか左側だけとかが変化しているわけではないね。
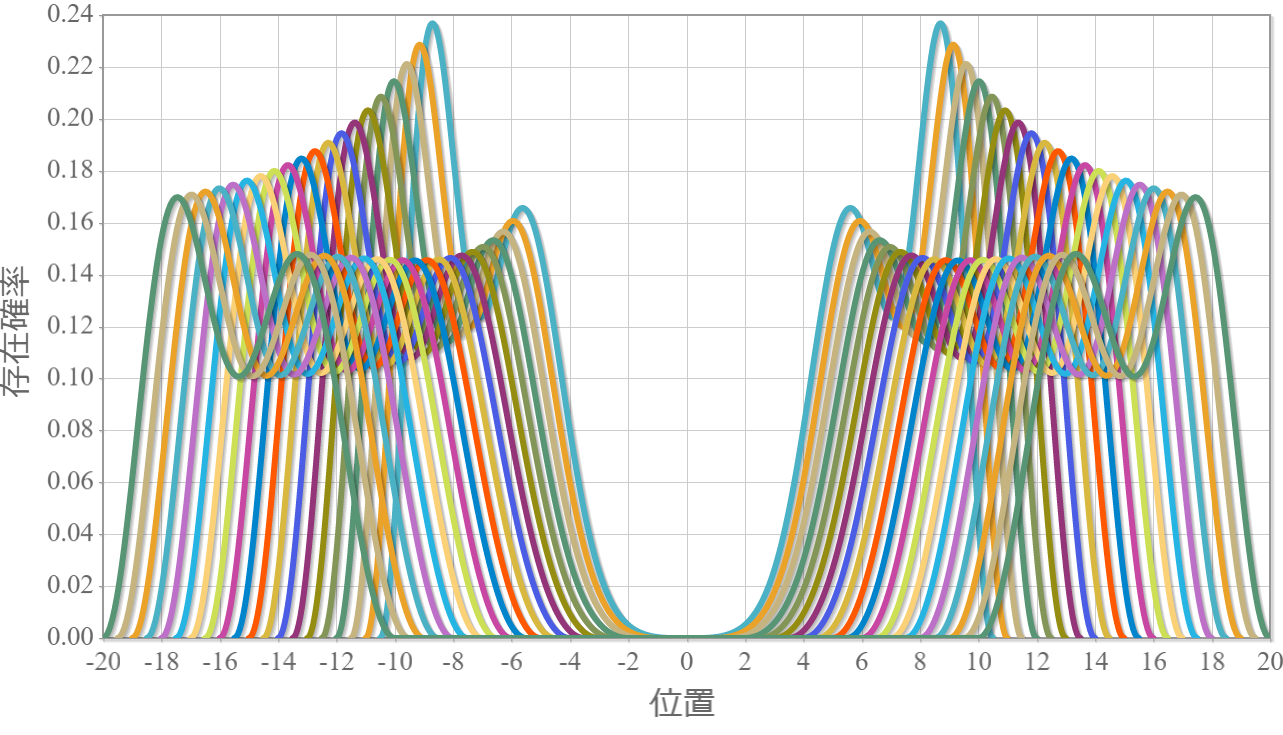
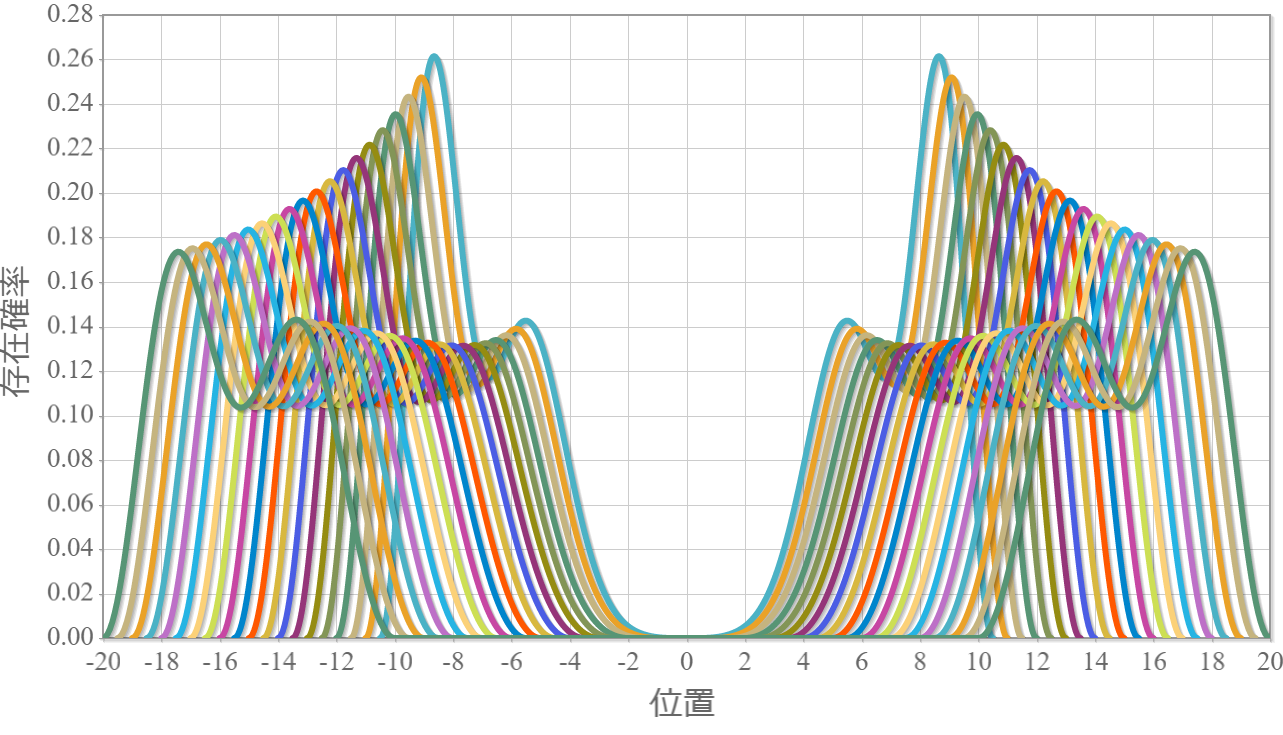
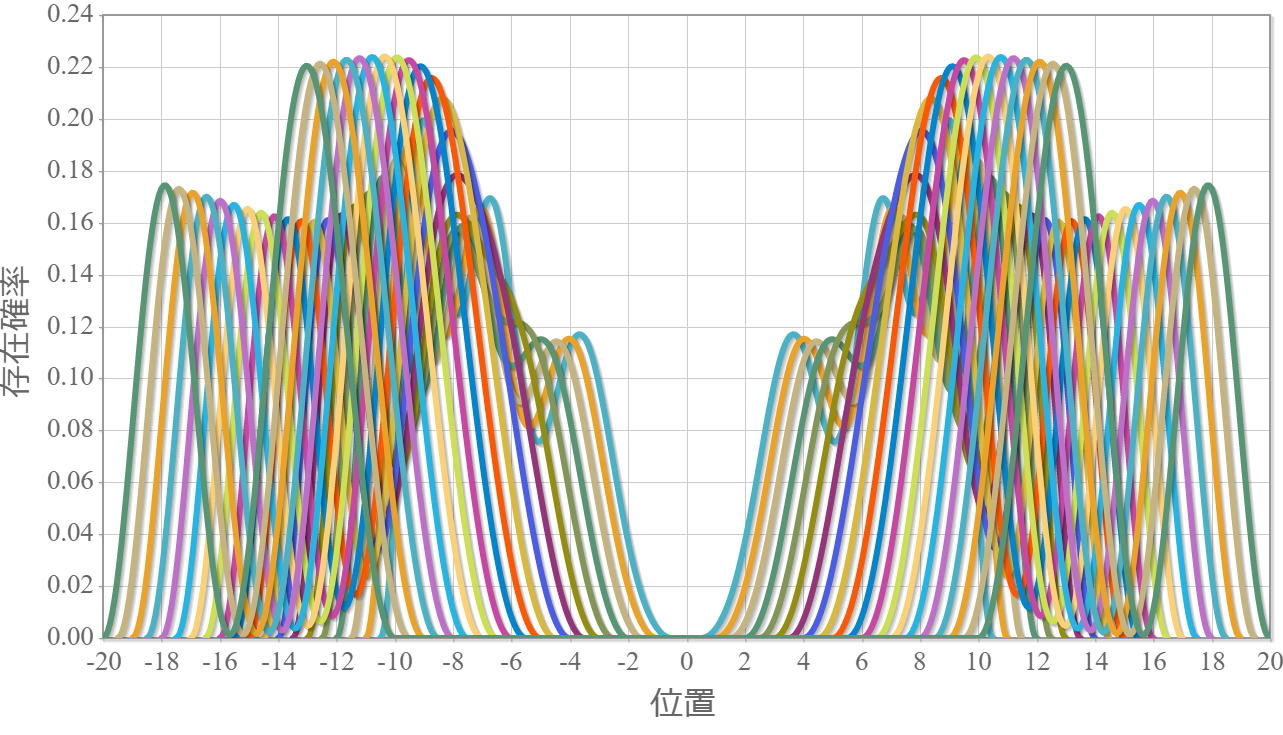
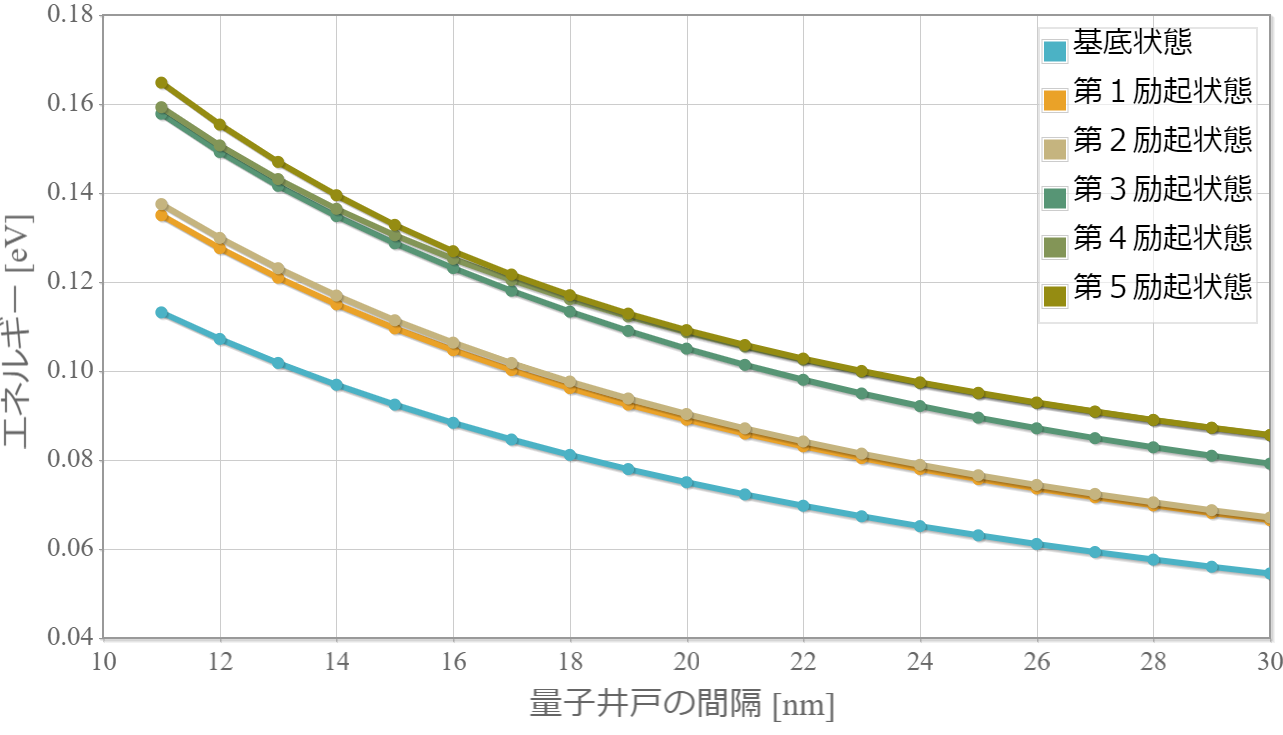
最後に、下から6つのエネルギー準位の量子井戸間隔に対する依存性を示しておくよ。間隔が広がるほど電子間に働くクーロン相互作用に大きさは反比例して小さくなっていくので、エネルギーも反比例して小さくなっていくね。そして、第1励起状態と第2励起状態、第4励起状態と第5励起状態は縮退していくね。
次回は、これに静電場を加えてみるね。本当に電気双極子モーメントは発生するのだろうか?ちょっと心配になってきたね。
