前回解説した内容を踏まえて、外部から加える磁場を1テスラとしたときの主量子数1から3までのエネルギー準位の計算結果を示すよ。水素原子の場合、外部磁場が1テスラでスピン―軌道相互作用の効果とゼーマン効果がどちらも $10^{-5}[{\rm eV}]$ 程度となるよ。
主量子数1(2状態)
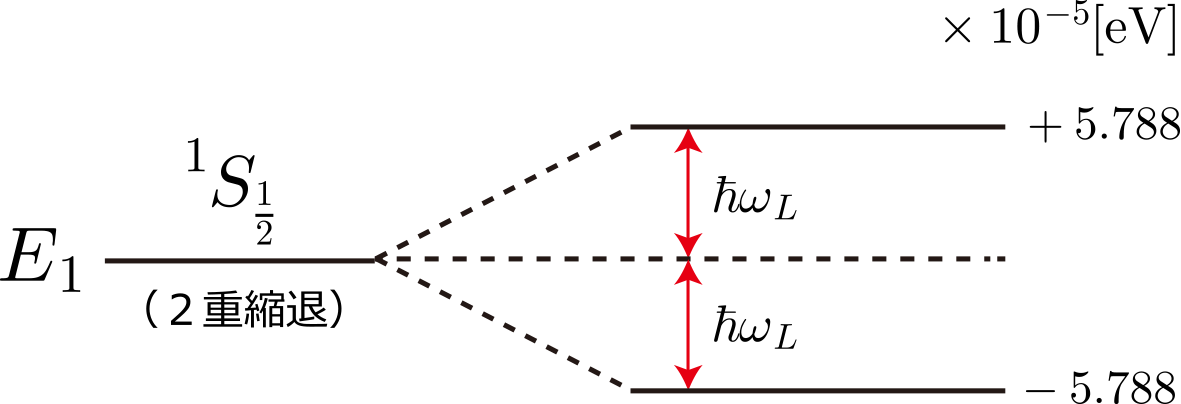
主量子数2(8状態)
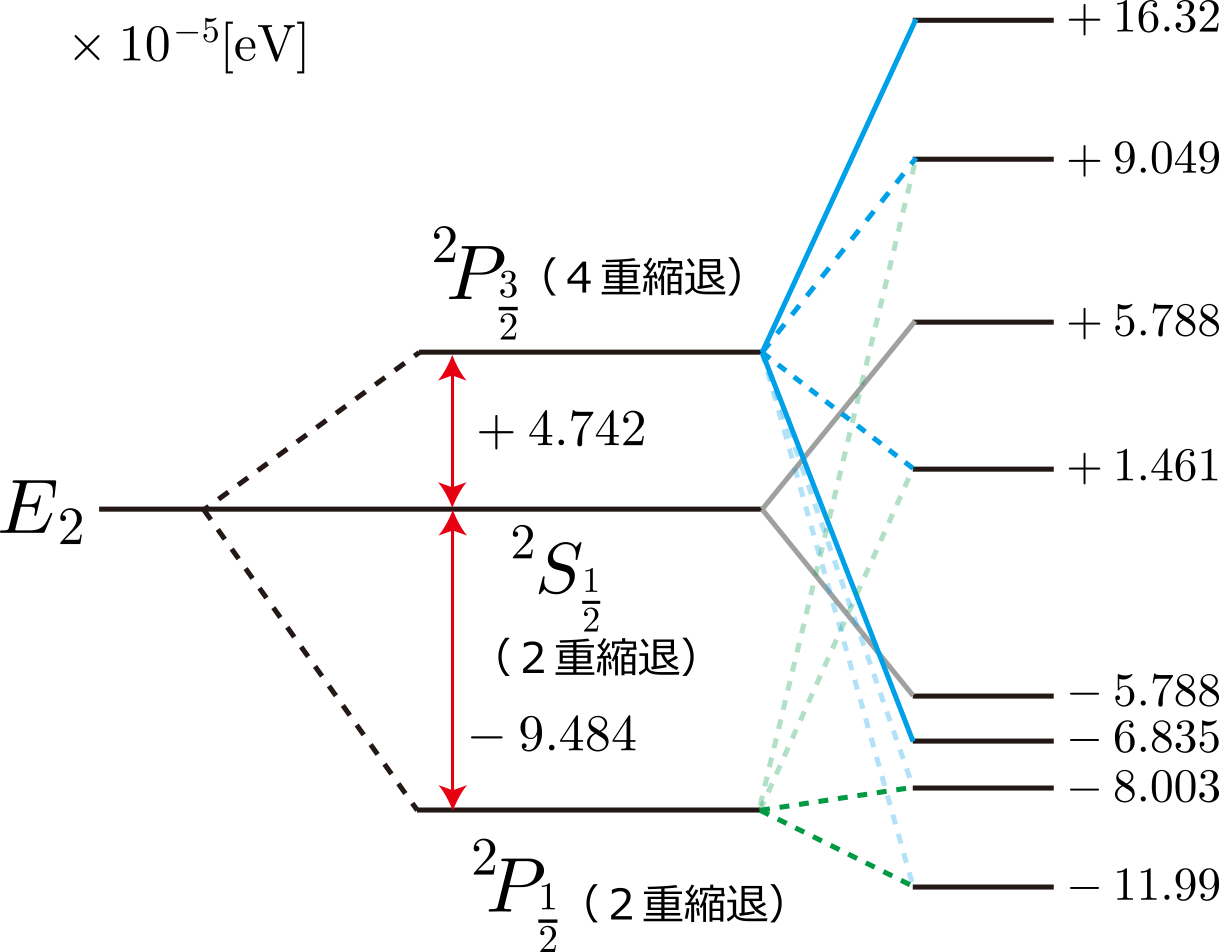
主量子数3(18状態)の上半分
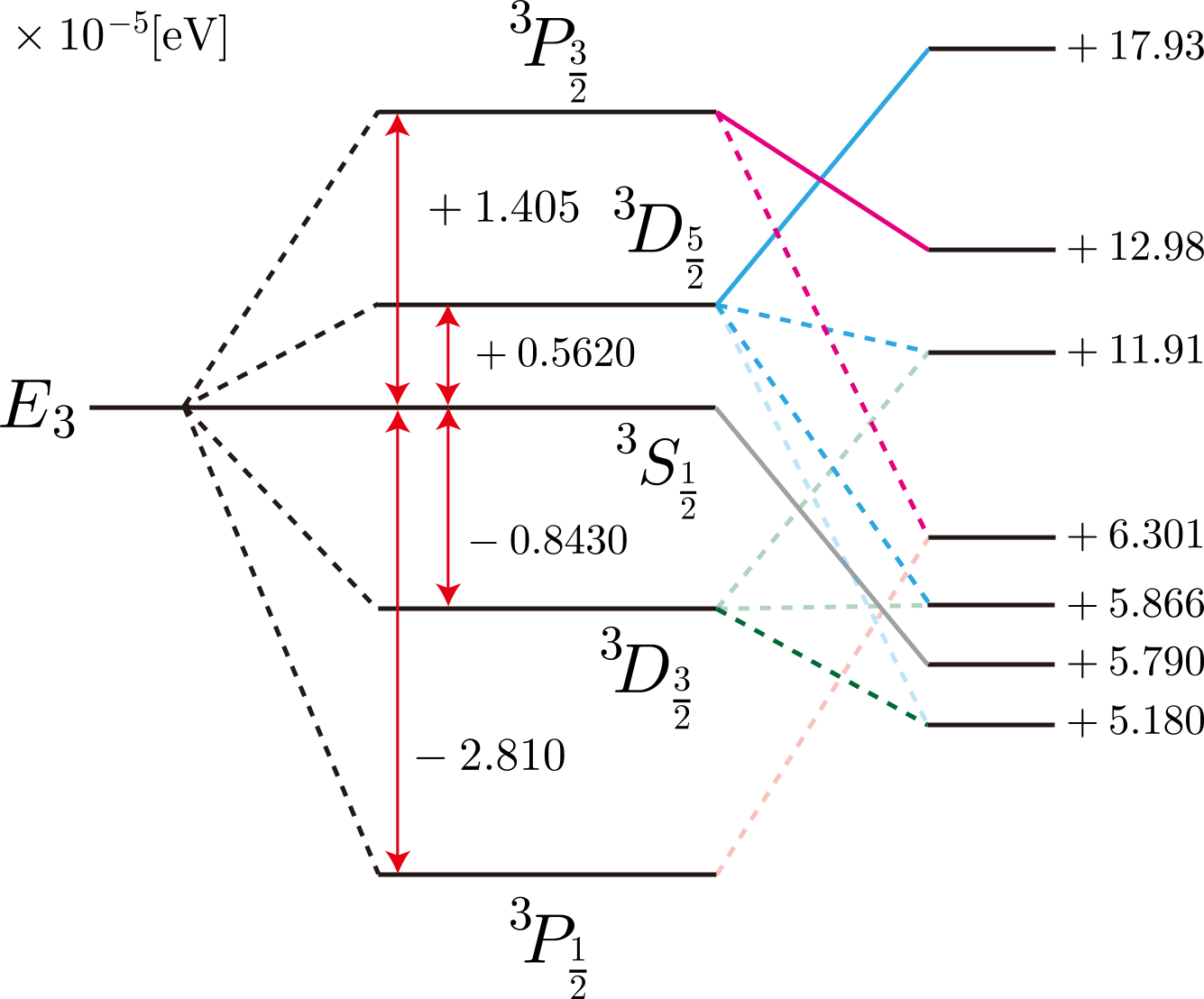
主量子数3(18状態)の下半分
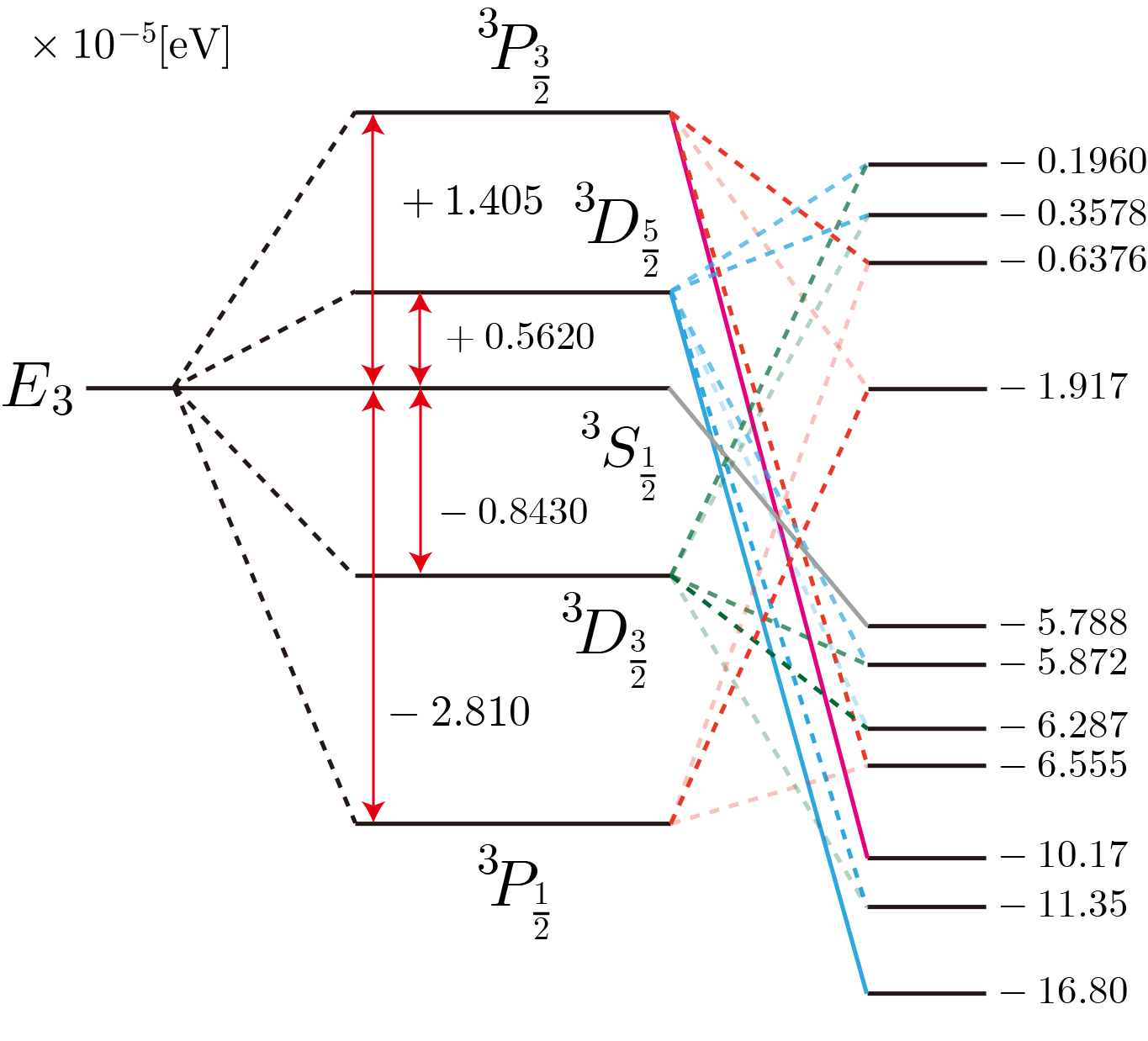

物理シミュレーションが趣味なシミュ君のページ
前回解説した内容を踏まえて、外部から加える磁場を1テスラとしたときの主量子数1から3までのエネルギー準位の計算結果を示すよ。水素原子の場合、外部磁場が1テスラでスピン―軌道相互作用の効果とゼーマン効果がどちらも $10^{-5}[{\rm eV}]$ 程度となるよ。




はじめに少し復習するよ。
スピン―軌道相互作用を考慮した水素原子のハミルトニアンは
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e^2}{8\pi \epsilon_0 c^2 r^3 m_e^2 }\,\hat{\boldsymbol{L}}\cdot\hat{\boldsymbol{S}}
\end{align}
だね。このハミルトニアンのエネルギー固有状態となる固有関数は、軌道角運動量とスピン角運動量を合成して生成した $\varphi_{n,l,j,m_j}$ だね。この場合の固有エネルギーは
\begin{align}
E = E_n + \frac{\hbar^2e^2}{16\pi \epsilon_0 c^2 r^3 m_e^2 }\left[ j(j+1) – l(l+1) – \frac{3}{4} \right] \int
\varphi_{nljm_j}^*\,\frac{1}{r^3}\, \varphi_{nljm_j} dV
\end{align}
だったね。これにさらに外部から磁場を加えると、ハミルトニアンに次のように表せるね。
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e^2}{8\pi \epsilon_0 c^2 r^3 m_e^2 }\,\hat{\boldsymbol{L}}\cdot\hat{\boldsymbol{S}} + \frac{eB_z}{2m_e} \left(\hat{L}_z+2\hat{S}_z\right) + \frac{e^2B_z^2}{8m_e} (x^2 + y^2)
\end{align}
このハミルトニアンに現れるゼーマン項の $\hat{L}_z$ と $\hat{S}_z$ はどちらも、先の固有関数 $\varphi_{nljm_j} $ では固有状態にならいんだよね。つまり、このハミルトニアンはたとえ最後の項を無視したとしても、解析的には固有状態を得られそうにないね。これまでと同様の手順で、固有状態をシミュレーションしてみよう!
先のハミルトニアン $\hat{H}$ の固有関数 $\Psi$ を 軌道角運動量とスピン角運動量を合成して生成した $\varphi_{nljm_j}$ で展開しよう。
\begin{align}
\Psi = \sum\limits_{n, l , j, m_j} a_{nljm_j}\varphi_{nljm_j}
\end{align}
ただし、$n, l, j, m_j$ の範囲は次のとおりだよ。
\begin{align}
0 \le &\ l < n \\
\left|l - \frac{1}{2}\right| \le &\ j \le l + \frac{1}{2} \\
-\left(\le l + \frac{1}{2}\right) \le &\ m_j \le l + \frac{1}{2}
\end{align}
シュレーディンガー方程式 $\hat{H}\psi = E\psi $ に代入して、展開係数を決定する方程式を導出しよう。ハミルトニアンを次のように対角成分 $H_0$ と非対角成分を含む $\hat{H}’$ に分けて、$\hat{H} = \hat{H}_0 + \hat{H}’$ と記述すると、シュレーディンガー方程式は次の用になるね。
\begin{align}
\sum\limits_{n, l , j, m_j} (E_n + \hat{H}’) a_{nljm_j}\varphi_{nljm_j} = E \sum\limits_{n, l , j, m_j} a_{nljm_j}\varphi_{nljm_j}
\end{align}
両辺に $\varphi^*_{n’l’j’m’_j}$ を掛けて、全空間で空間積分すると、展開係数 $a_{njlm_j}$ に関する連立方程式が得られるね。
\begin{align}
E_{n’} a_{n’l’j’m’_j} + \sum\limits_{n, l , j, m_j} a_{nljm_j} \int \varphi^*_{n’l’j’m’_j}\hat{H}’ \varphi_{nljm_j} dV = E
a_{n’l’j’m’_j}
\end{align}
あとは、これを連立方程式を数値的に解くだけだね。