独立電子近似の場合、ヘリウム原子の2つの電子の波動関数は、個々の水素様原子( $Z=2$ )の波動関数の積を用いて、空間対称(スピン3重項/パラ)あるいは空間反対称(スピン1重項/オルト)の2つの状態をとるよ。具体的な波動関数の表式はそれぞれ
\begin{align}
\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) + \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) – \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\end{align}
と表されるね。この波動関数は各粒子ごとに3次元で合計で6次元の関数なので、これを描画するには工夫が必要になるよ。1番基本的な考え方は、空間位置 $ \boldsymbol{r} $ に粒子1あるいは粒子2が存在する空間確率密度を
\begin{align}
\rho( \boldsymbol{r} ) = \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}) |^2 dV_1 + \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, \boldsymbol{r}_2) |^2 dV_2
\end{align}
と定義することで、空間分布を計算することができるね。ただし、これを先の $\chi^{(S)}$ と $\chi^{(A)}$ に適用すると、
\begin{align}
\rho^{(S)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2\\
\rho^{(A)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2
\end{align}
となって、それぞれの粒子の空間分布の和となるね。ヘリウム原子の低エネルギーの状態は、粒子の片方は必ず $(n,l,m)=(1,0,0)$ に存在するので、先の空間確率密度を数値的に計算すると、他方の粒子がどの準位に存在したとしても、 $|\varphi_{100}(\boldsymbol{r})|^2 >> |\varphi_{nlm}(\boldsymbol{r})|^2 $ となって、実質的に $|\varphi_{100}(\boldsymbol{r})|^2$ となってしまうね。これは、2つの粒子が存在する確率が $|\varphi_{100}(\boldsymbol{r})|^2$ で表される領域に集中していることを意味しているよ。
そこで今回は、粒子の1つが $\varphi_{100}(\boldsymbol{r})|$の最も確率の高い原点( $\boldsymbol{r}_1=0$ あるいは $\boldsymbol{r}_2=0$ )に存在するとして、他方の粒子の空間確率密度
\begin{align}
\rho^{(S)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, 0)|^2 \\
\rho^{(A)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r},0)|^2
\end{align}
を定義して、空間分布を描画したよ。ちなみに両者とも第1項目と第2項目の値は同じ値となるよ。
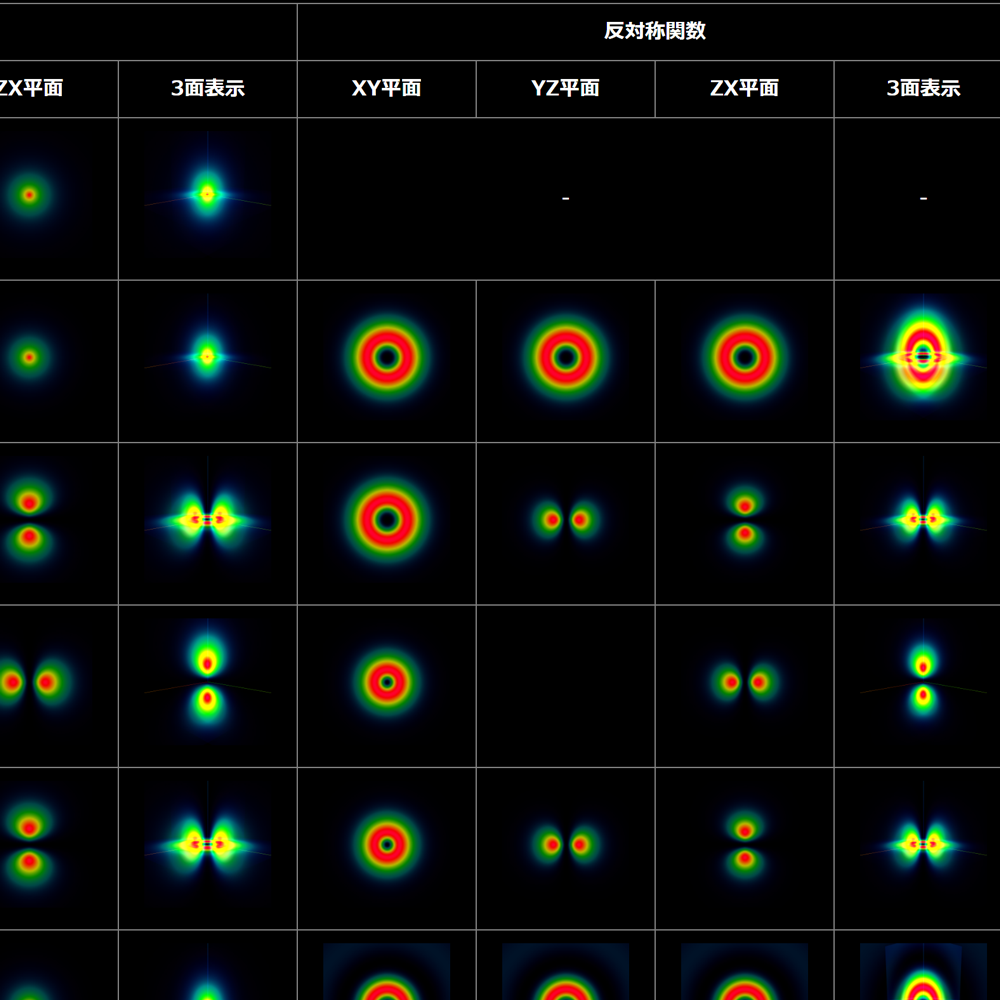
(※実際の表はこちらのページを見てね!)
上記の結果は単に $|\varphi_{nlm}(\boldsymbol{r})|^2$ を計算した結果に似ているけれども異なるよ。空間対称関数と空間反対称関数では、概ね同じだけれども顕著に異なるのが、2個目の粒子の状態が $(n,l,m) =(2,0,0)$ や $(n,l,m) =(3,0,0)$ で、原点を中心に存在する場合だね。これは、空間対称関数の場合には、同じ領域に居ようとするけれども、空間反対称関数の場合には、互いに避けようとする結果だね。次回は、電子間の相互作用を加味した波動関数を描画するよ。
