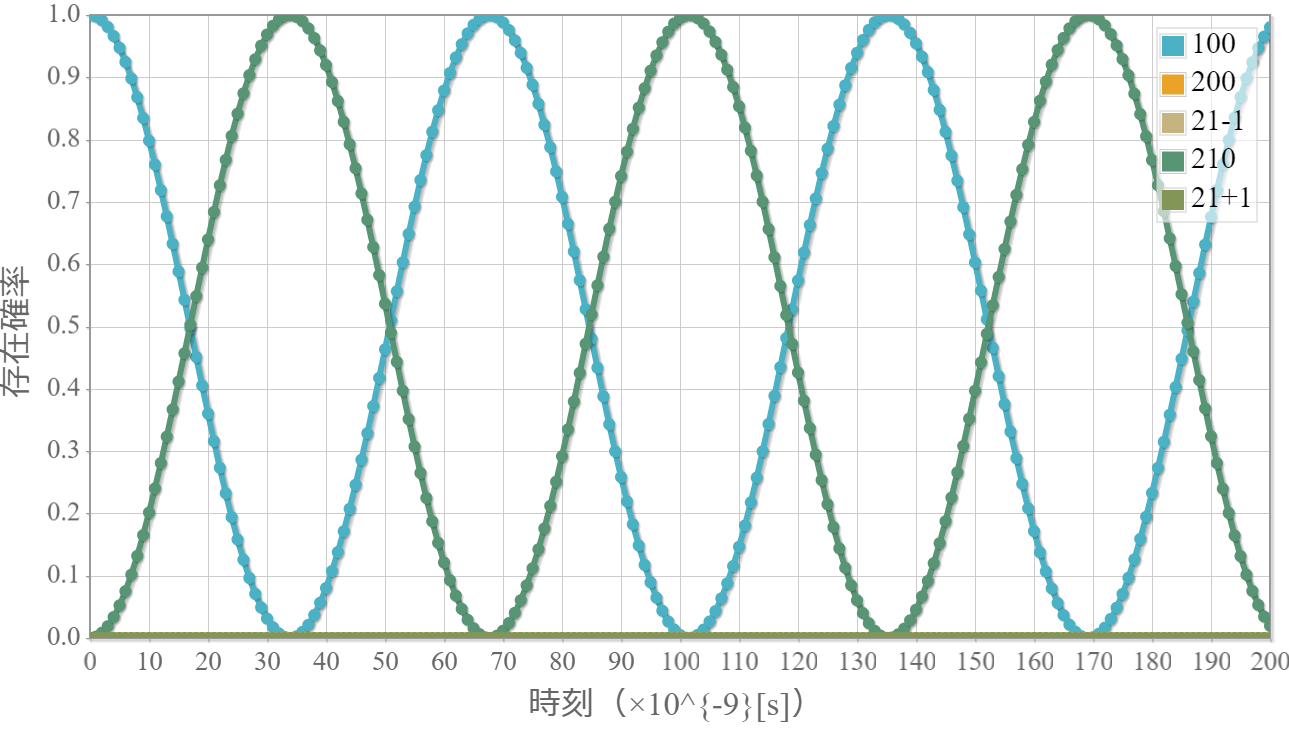
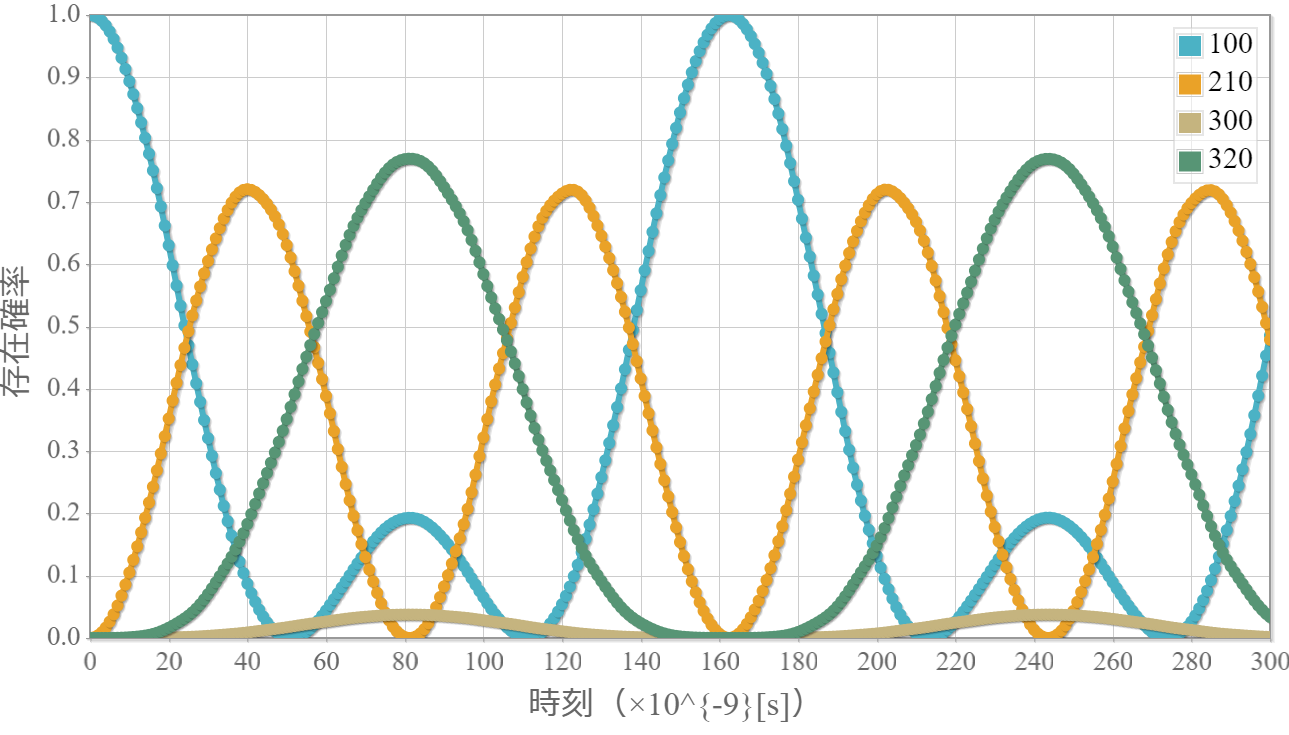
ポテンシャルが0のシュレーディンガー方程式の解である平面波は前回示したね。この平面波を重ね合わせることで、任意の波形を作ることができるよ。今回は、波数分布をガウス分布とした波束の作り方を解説するよ。波束は異なる波数(速度)の平面波の重ね合わせで作ることができるよ。中心波数 $k_0$ としたときの表式は次のとおりだよ。
\begin{align}
\psi(x,t)= \frac{1}{ \sqrt{2\sigma \pi L}}\int dk\, \exp\left[ ik(x-x_0) -i\omega t-\left(\frac{ k-k_0 }{2\sigma} \right)^2 \right]
\end{align}
$k_0$ は波束が進む速度 $v$ と、 $v_0 =p_0 / m_e = \hbar k_0 / m_e$ の関係があるよ。
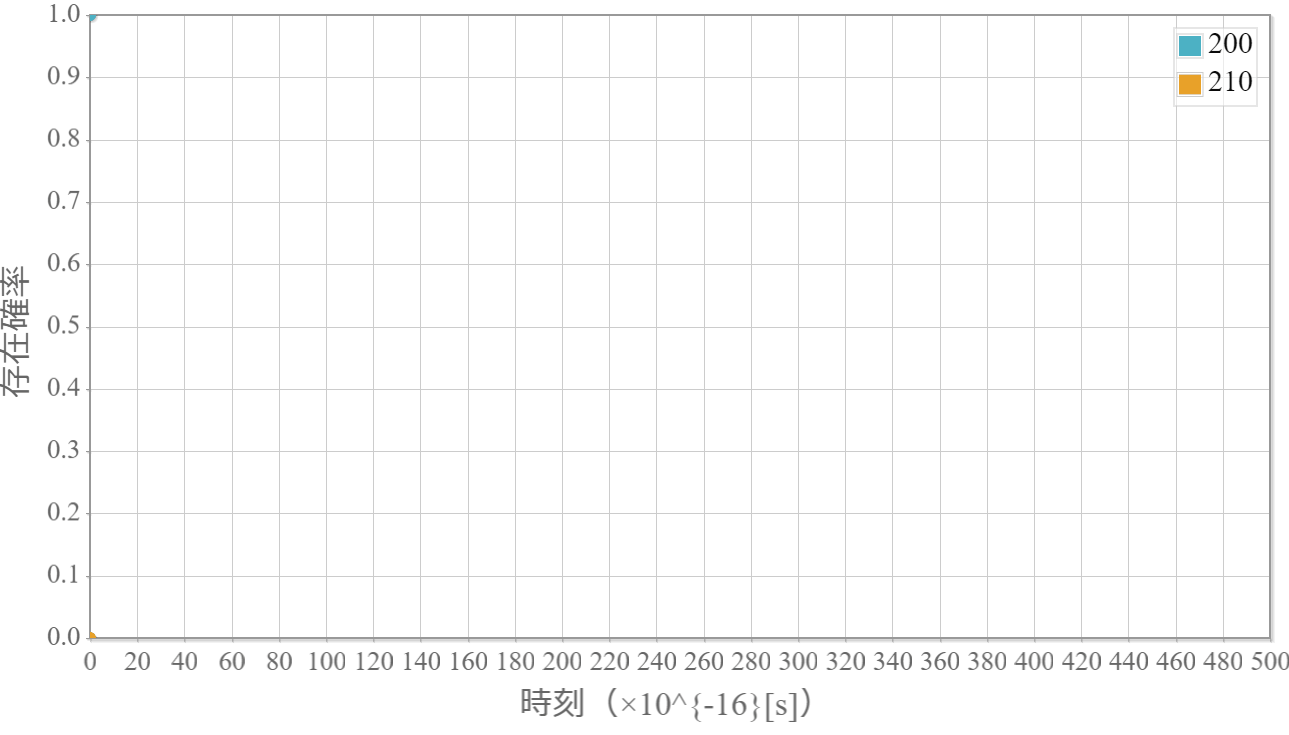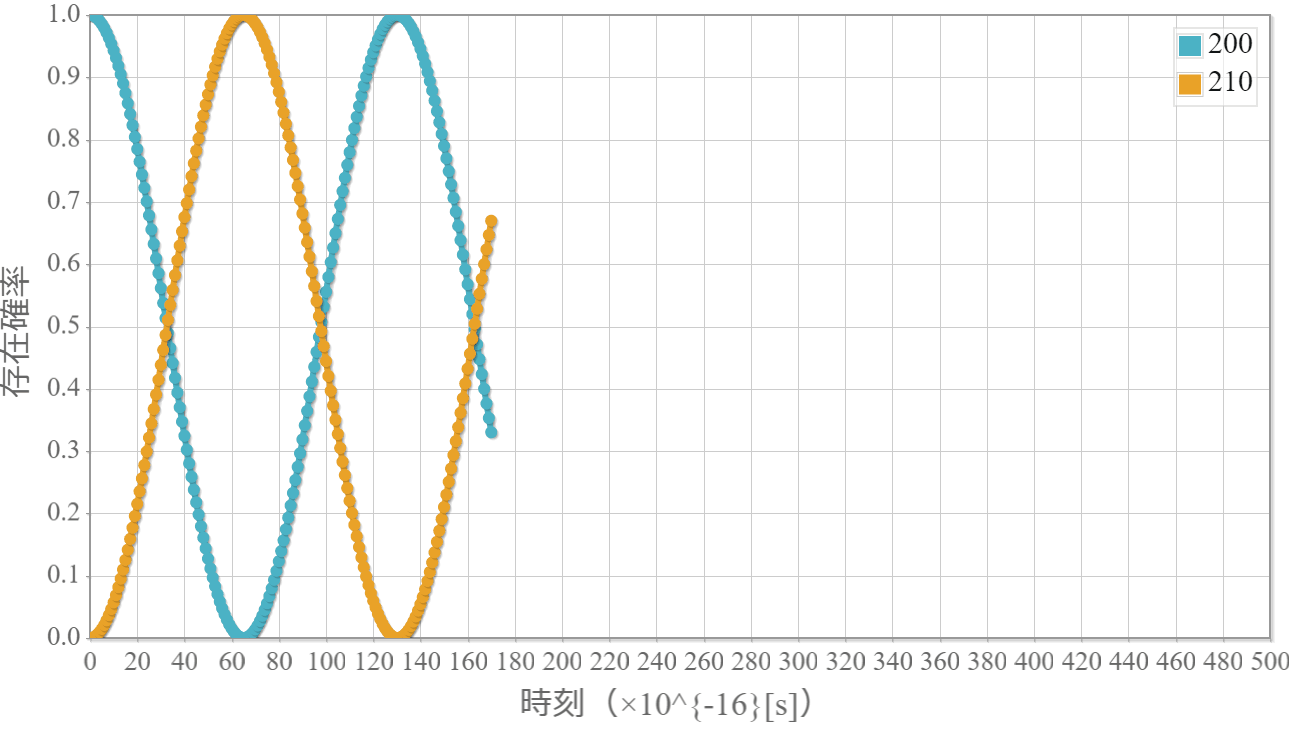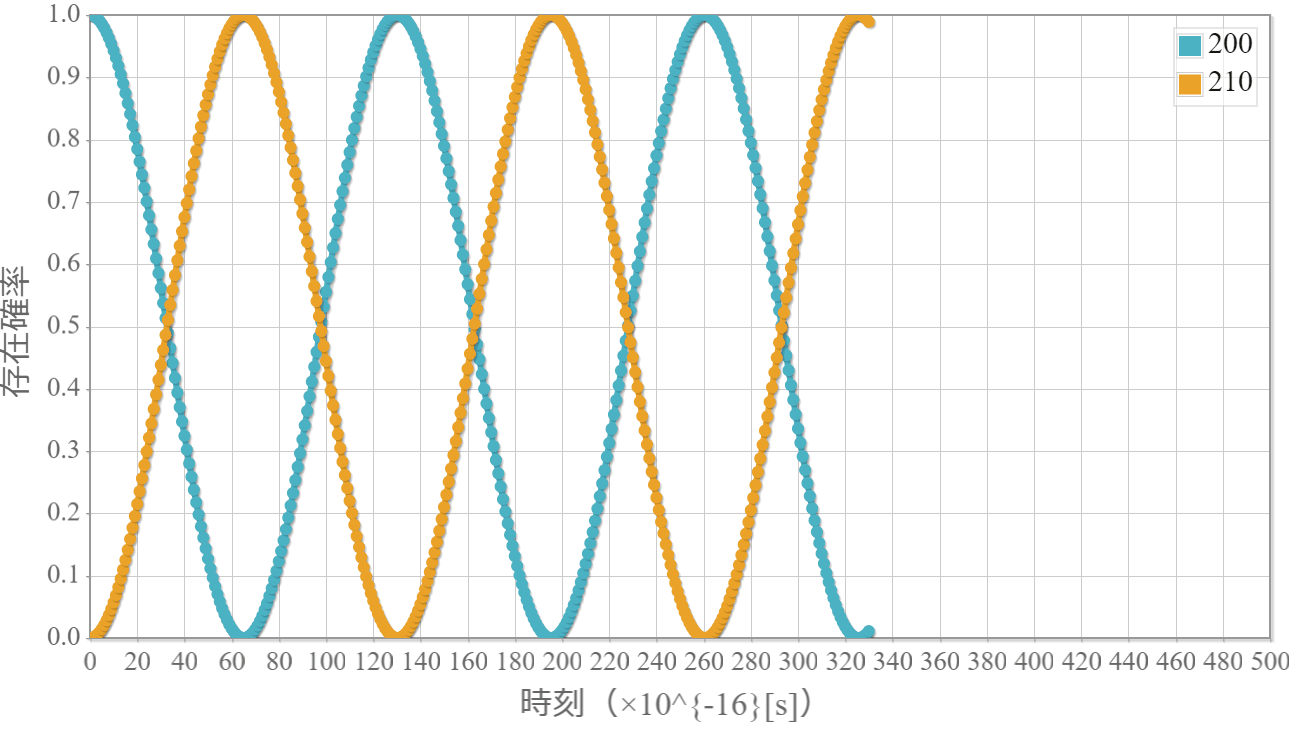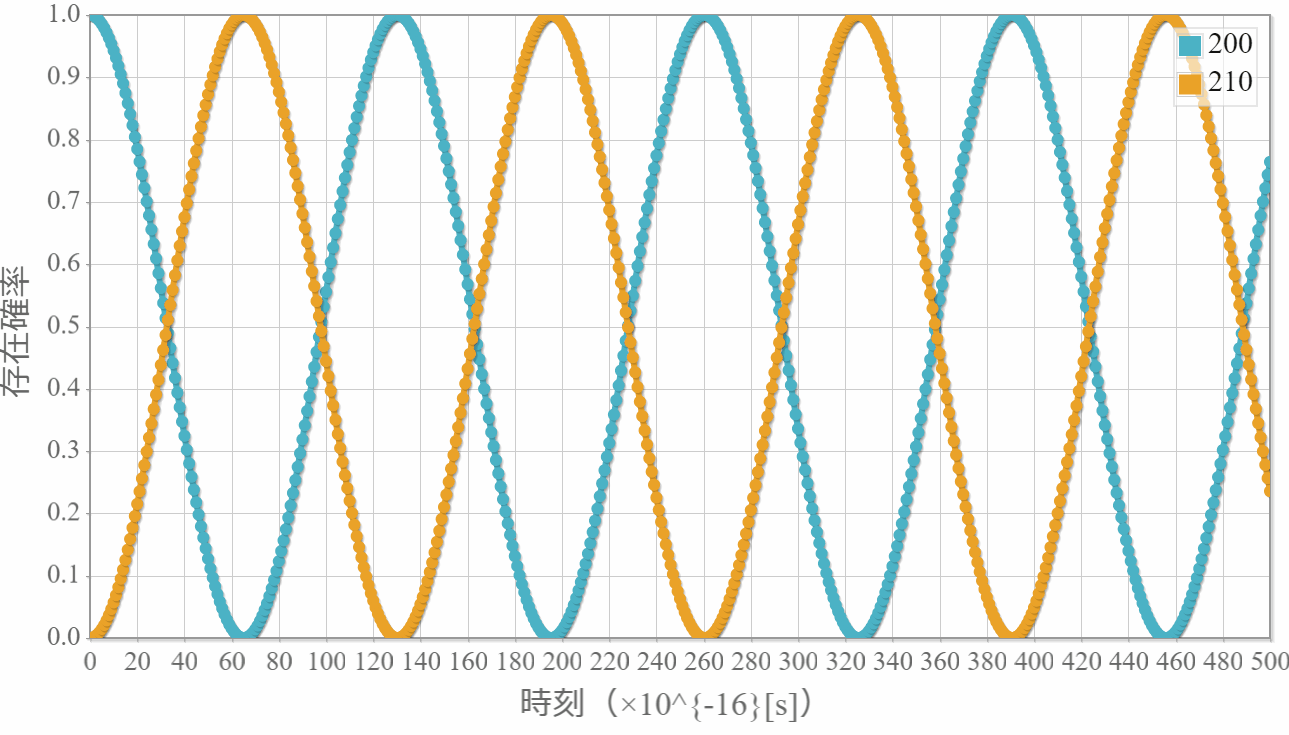
波束の運動の計算結果
波束の中心エネルギー: $E_0 = 10[{\rm eV}]$
空間スケール: $10^{-11}[{\rm m}]$ //横軸の値
時間スケール: $10^{-16}[{\rm s}]$ //動画1コマの時間間隔
波束の中心エネルギー: $E_0 = 0[{\rm eV}]$
空間スケール: $10^{-11}[{\rm m}]$ //横軸の値
時間スケール: $4\times 10^{-15}[{\rm s}]$ //動画1コマの時間間隔
ちなみに、どんな波束も時間とともに広がっていくよ。その理由は分散関係 $\omega$ が $k$ に比例しないからだよ。
プログラムソース(C++)
////////////////////////////////////////////////////////////////////
// 【第3回】「波束」の作り方
////////////////////////////////////////////////////////////////////
#define _USE_MATH_DEFINES
#include <iostream>
#include <fstream>
#include <sstream>
#include <iomanip>
#include <string>
#include <complex>
/////////////////////////////////////////////////////////////////
//物理定数
/////////////////////////////////////////////////////////////////
//光速
const double c = 2.99792458E+8;
//真空の透磁率
const double mu0 = 4.0*M_PI*1.0E-7;
//真空の誘電率
const double epsilon0 = 1.0 / (4.0*M_PI*c*c)*1.0E+7;
//プランク定数
const double h = 6.6260896 * 1.0E-34;
double hbar = h / (2.0*M_PI);
//電子の質量
const double me = 9.10938215 * 1.0E-31;
//電子ボルト
const double eV = 1.60217733 * 1.0E-19;
//複素数
const std::complex<double> I = std::complex<double>(0.0, 1.0);
/////////////////////////////////////////////////////////////////
//物理系の設定
/////////////////////////////////////////////////////////////////
//空間分割数
const int Nx = 500;
//空間分割サイズ
double dx = 1.0E-10;
//重ね合わせの数
const int N = 200;
//パルスの幅
double delta_x = 1.0E-8;
double sigma = 2.0*sqrt(2.0*log(2.0)) / (delta_x);
//波数の間隔
double dk = 30.0 / (delta_x * double(N + 1));
//電子波のエネルギー
const double E0 = 10.0 * eV;
//波数の中心
double k0 = sqrt(2.0 * me * E0 / pow(hbar, 2));
//角振動数の中心
double omega0 = hbar / (2.0*me) * pow(k0, 2);
//計算時間の幅
const int ts = 0, te = 300;
//時間間隔
double dt = 1.0 * 1.0E-16;
/////////////////////////////////////////////////////////////////
const int precision_N = 4;
int main() {
//出力ストリームによるファイルオープン
std::ofstream fout;
fout.open("wave.txt");
fout << "#x:位置" << std::endl;
fout << "#y:確率振幅" << std::endl;
fout << "#legend: 実部 虚部 絶対値" << std::endl;
fout << "#showLines: true true true" << std::endl;
fout << "#showMarkers: false false false" << std::endl;
fout << "#xrange:" << -Nx / 2 << " " << Nx / 2 << " " << Nx / 10 << std::endl;
fout << "#yrange:" << -0.30 << " " << 0.30 << " " << 0.1 << std::endl;
//各時刻における計算を行う
for (int tn = ts; tn <= te; tn++) {
double t_real = dt * double(tn);
std::cout << tn << std::endl;
fout << "#coma:" << tn << std::endl;
for (int nx = 0; nx <= Nx; nx++) {
double x = dx * (nx - Nx/2);
std::complex<double> Psi = std::complex<double>(0.0, 0.0);
for (int jz = 0; jz <= N; jz++) {
double k = (k0 + dk * double(jz - N / 2));
double omega = hbar / (2.0*me) * pow(k, 2);
Psi += exp(I*(k*x - omega * t_real)) * exp(-1.0 / 2.0 * pow((k - k0) / sigma, 2));
}
Psi = Psi / double(N);
fout << std::setprecision(precision_N);
fout << x / dx << " " << Psi.real() << " " << Psi.imag() << " " << abs(Psi) << std::endl;
}
fout << std::endl;
}
fout.close();
}