以前解説したハミルトニアンを用いて、水素原子の基底状態の電子に電磁波(古典・直線偏光)を入射したの様子をシミュレーションしたよ。結果を示すね。
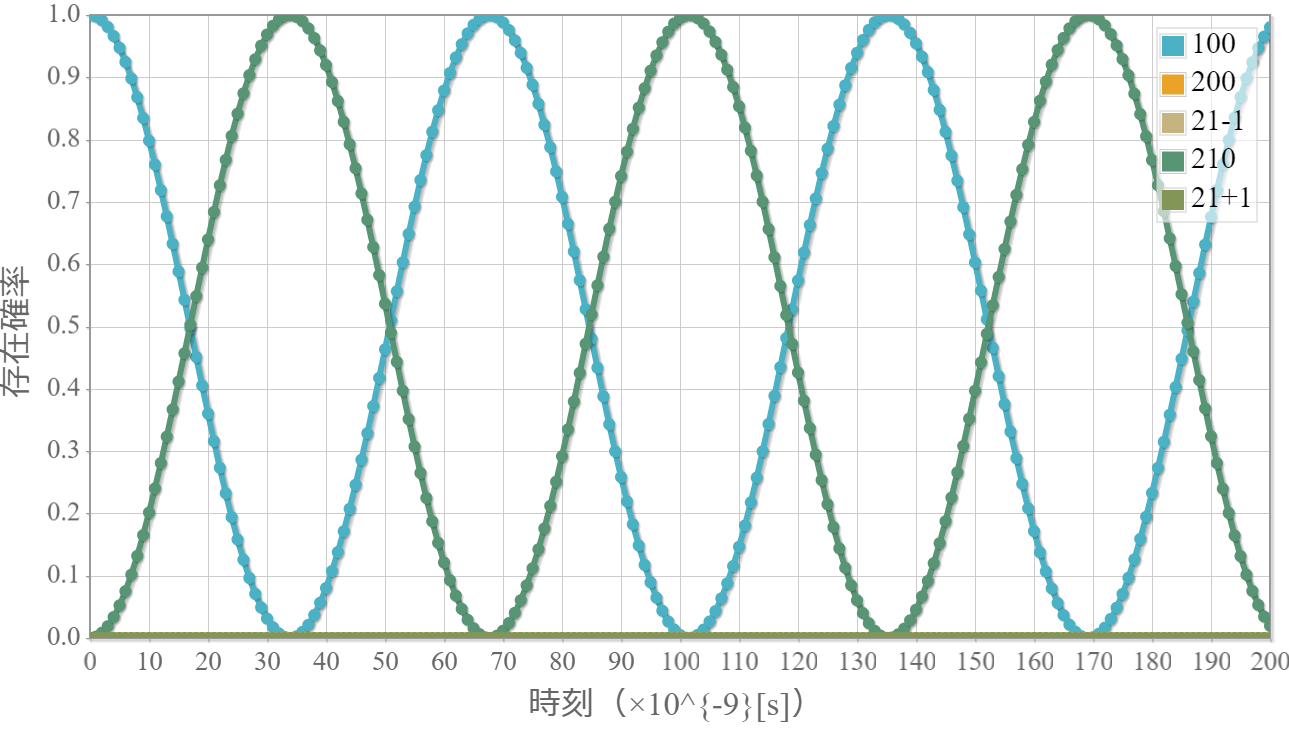
角振動数 $\omega_{12} = (E_2-E_1)/\hbar$ の電磁波を入射
次のグラフは、基底状態と第1励起状態のエネルギー準位の差に対応する電磁波を入射した結果だよ。$ \varphi_{100} $ と $ \varphi_{210} $ の間でラビ振動している様子が分かるね。
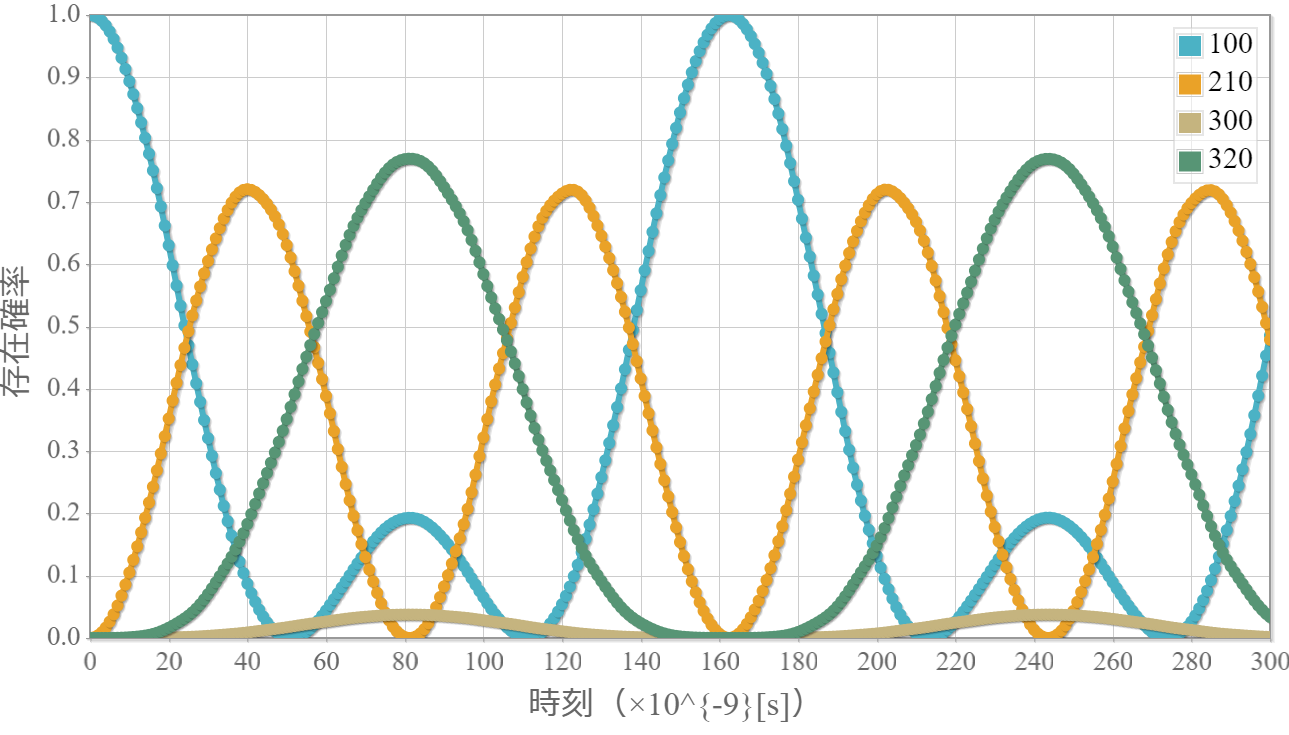
角振動数 $\omega_{12} = (E_2-E_1)/\hbar$ と $\omega_{23} = (E_3-E_2)/\hbar$の電磁波を入射
次のグラフは、基底状態と第1励起状態のエネルギー準位の差に対応する電磁波と、第1励起状態と第2励起状態ののエネルギー準位の差に対応する電磁波を同時に入射した結果だよ。$ \varphi_{100} $ と $ \varphi_{210} $ に加えて、$ \varphi_{100} $ から直接遷移することができない $ \varphi_{300} $ と $ \varphi_{320} $ にも励起しているね。このように、直接遷移が許されない状態が加わっても、存在確率が周期的に振動するのはちょっと意外だね。
次回は、円偏光の電磁波を入射するよ。
