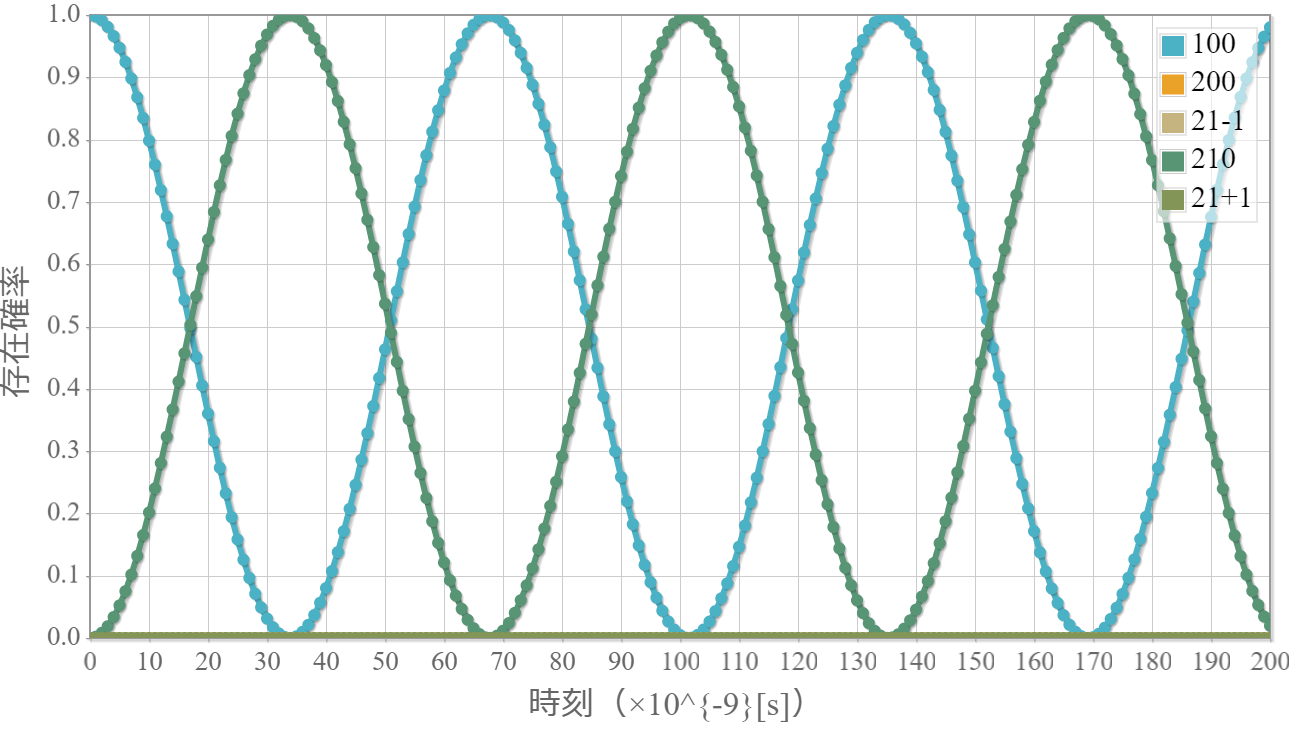
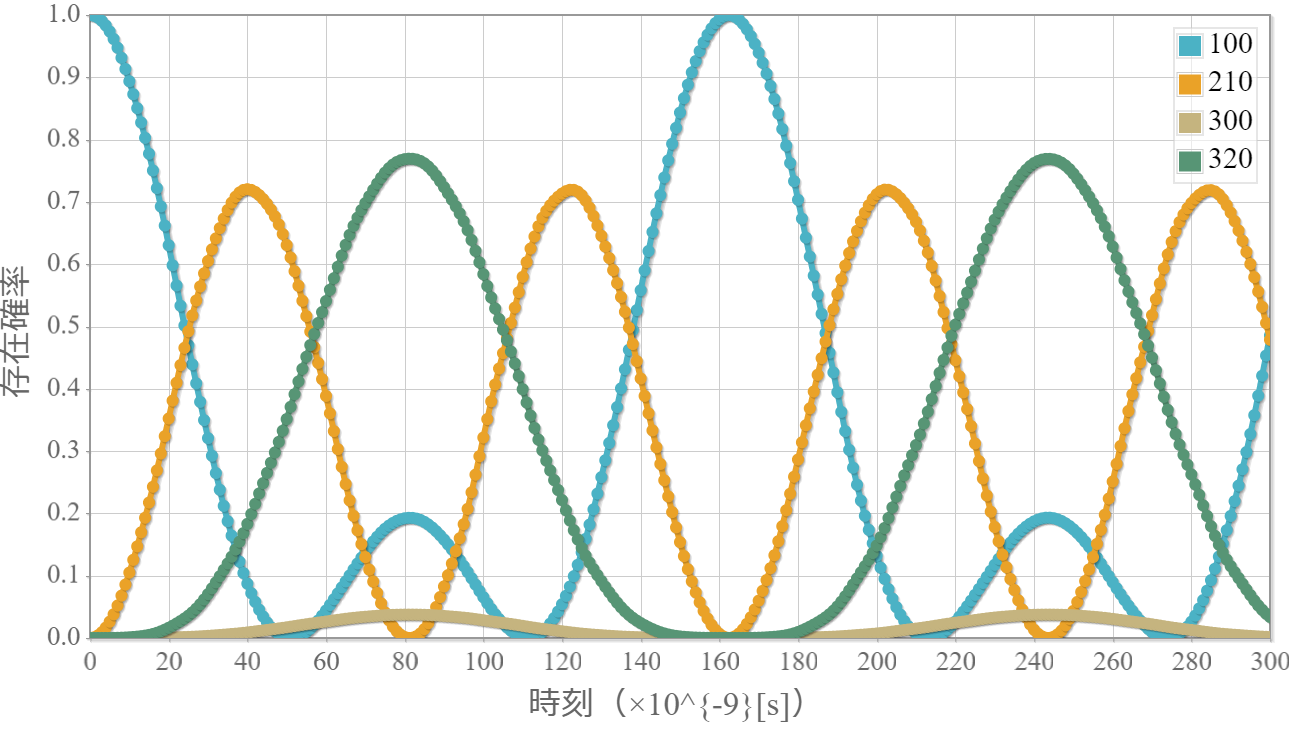
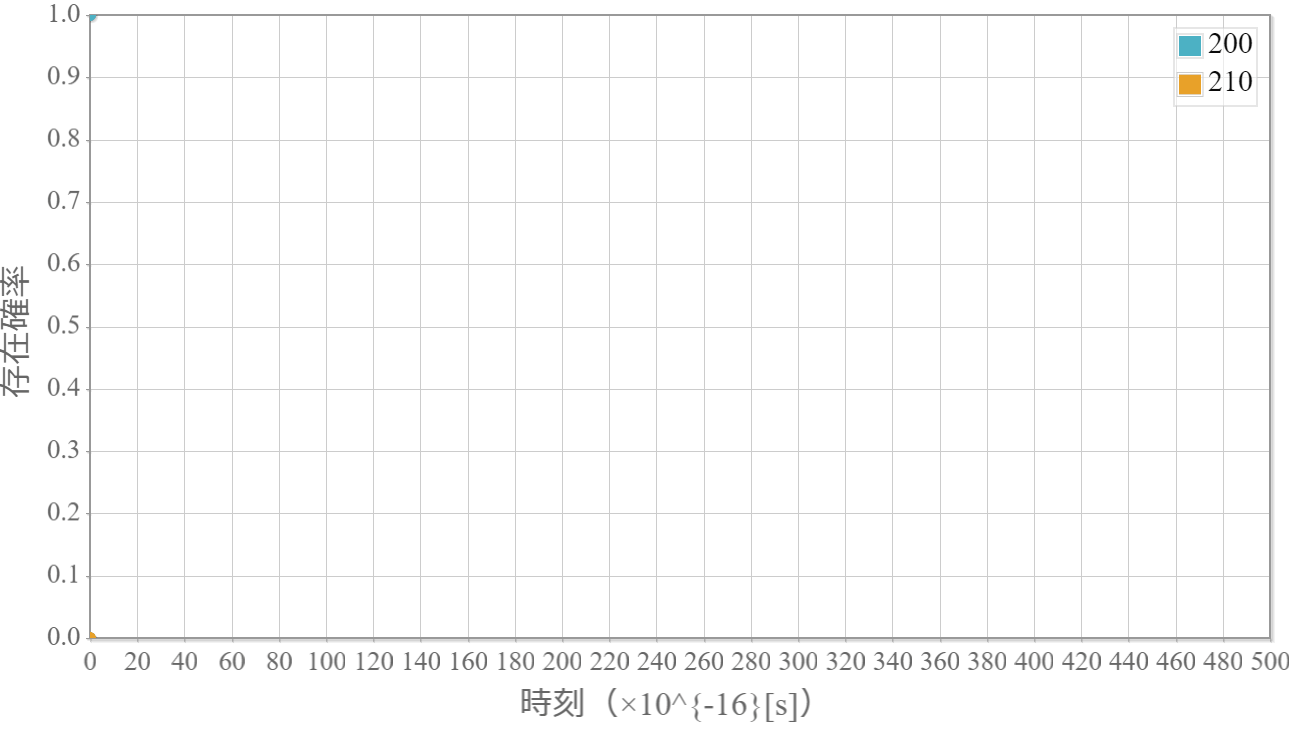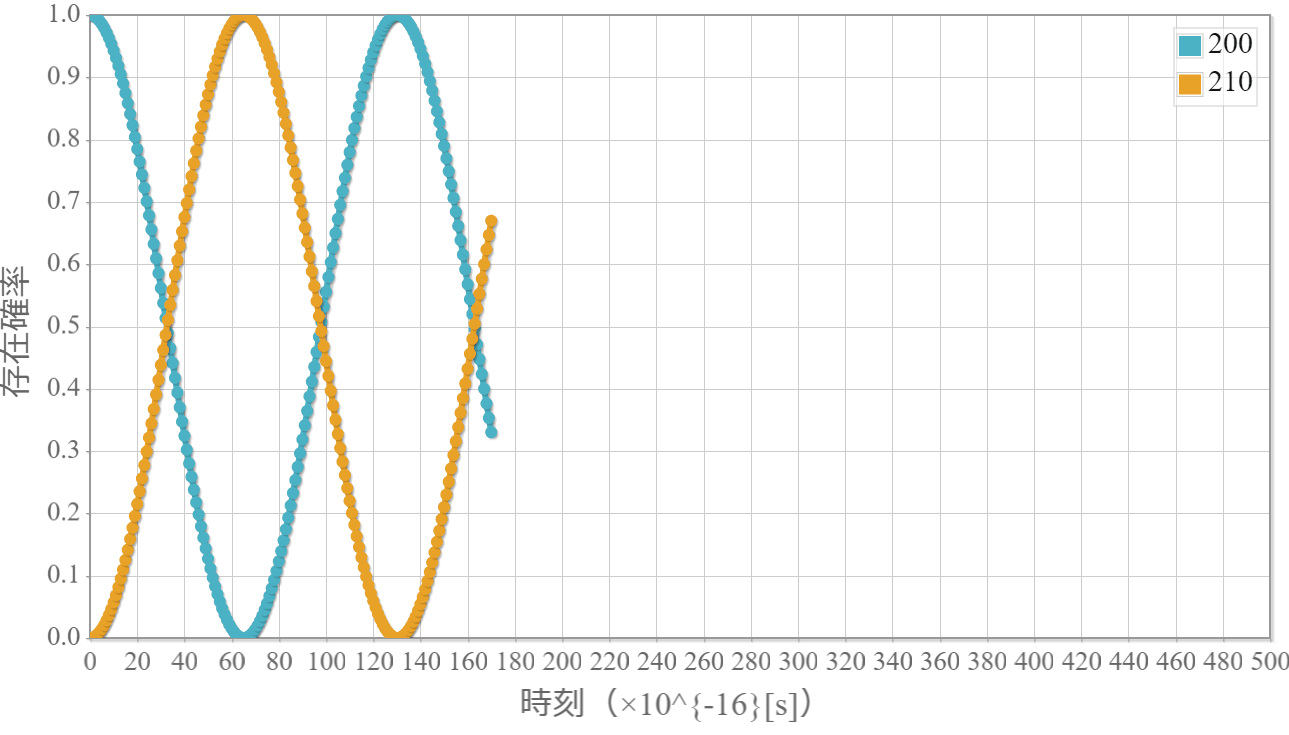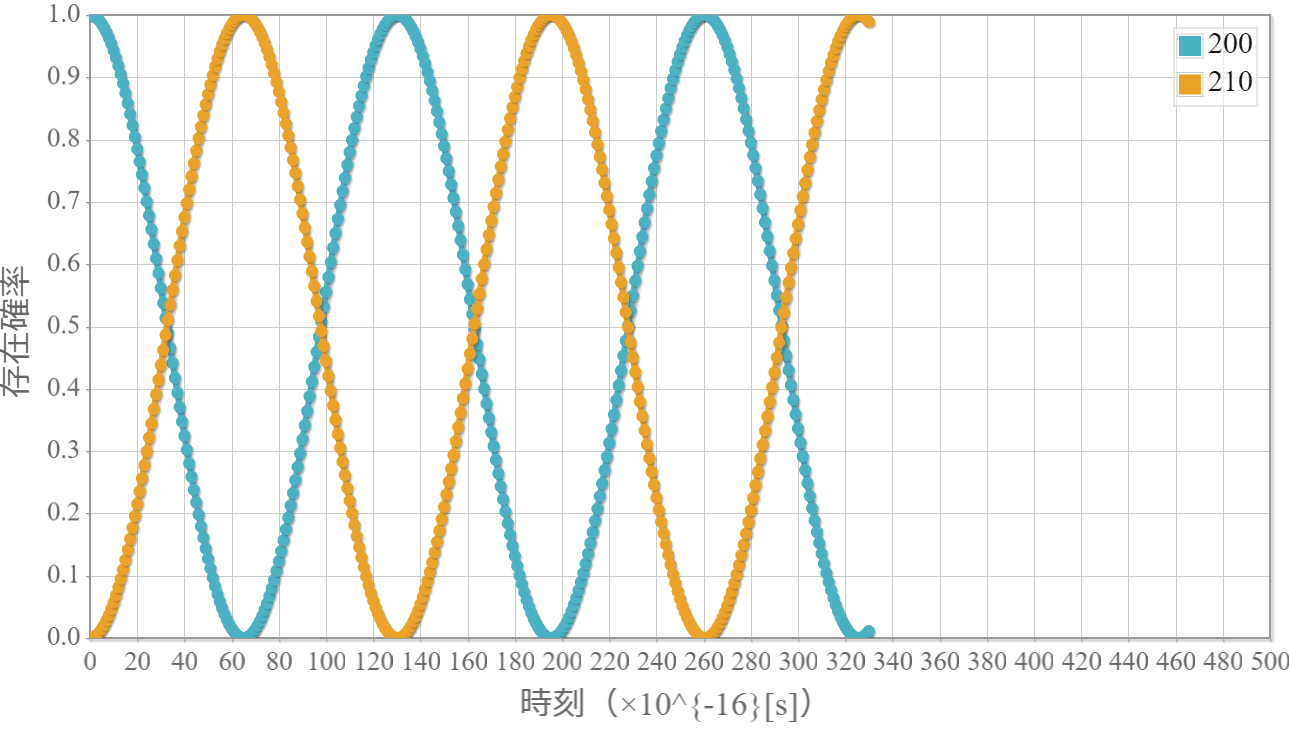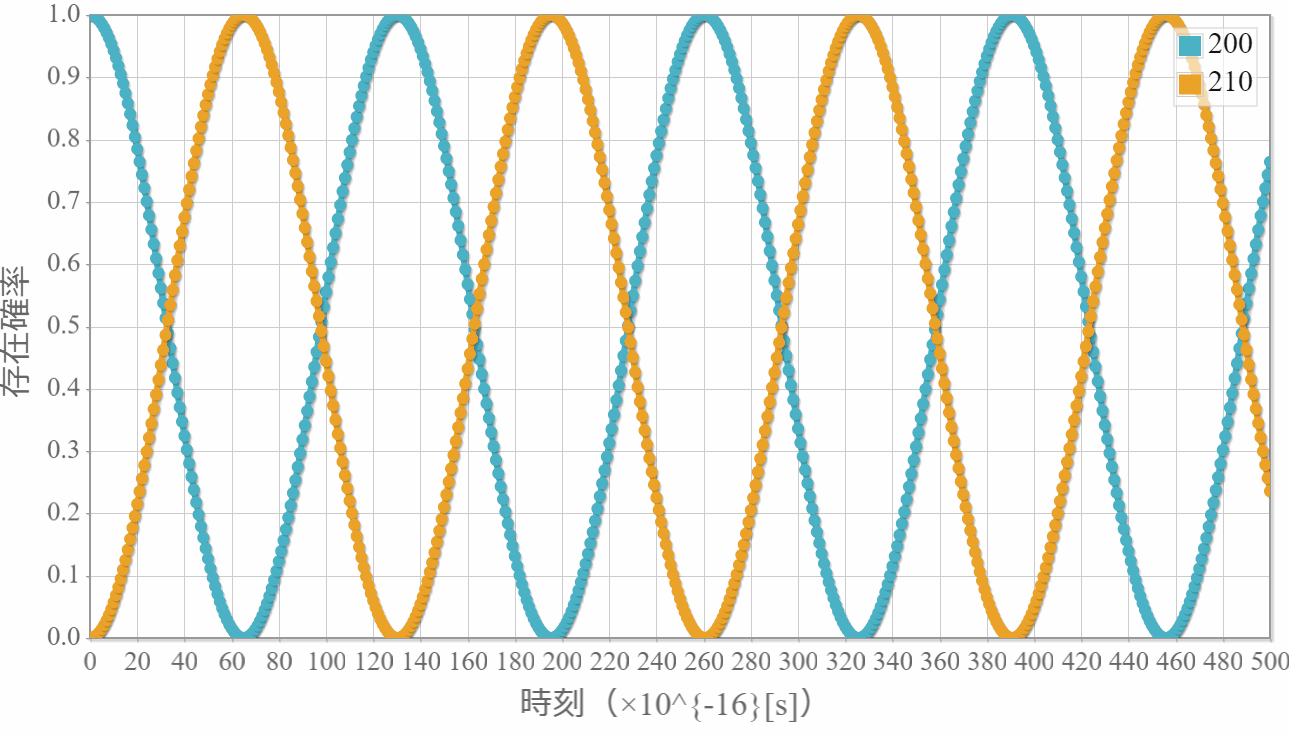
ポテンシャルが0のシュレーディンガー方程式の解は、平面波って呼ばれる解になるよ。
平面波の表式(1次元)
波数 $k$、角振動数 $\omega$ としたときの位置 $x$、時刻 $t$ の波動関数 $\Psi(x,t)$ だよ。
\begin{align}
\Psi(x,t) = A e^{i k x – i \omega i } + B e^{i k x + i \omega t}
\end{align}
$k$ と $\omega$ はエネルギー $E$ と
\begin{align}
k = \sqrt{\frac{2mE}{\hbar^2}} \ , \ \omega = \frac{E}{\hbar}
\end{align}
と関係があるから、$k$ と $\omega$ は独立ではなくて
\begin{align}
\omega = \frac{\hbar k^2}{2m}
\end{align}
という分散関係って呼ばれる関係もあるね。
特別な場合の計算結果
電子のエネルギー $E = 0.25, 1.0, 4.0 [{\rm eV}] $ の平面波の実部の様子を可視化するためのデータ出力用プログラムソースだよ。
プログラムソース(C++)
////////////////////////////////////////////////////////////////////
// 自由空間中の粒子
////////////////////////////////////////////////////////////////////
#define _USE_MATH_DEFINES
#include <math.h>
#include <stdlib.h>
#include <iostream>
#include <fstream>
#include <sstream>
#include <string>
#include <stdio.h>
/////////////////////////////////////////////////////////////////
//物理定数
/////////////////////////////////////////////////////////////////
//プランク定数
const double h = 6.6260896 * 1.0E-34;
double hbar = h / (2.0*M_PI);
//電子の質量
const double me = 9.10938215 * 1.0E-31;
//電子ボルト
const double eV = 1.60217733 * 1.0E-19;
/////////////////////////////////////////////////////////////////
//物理系の設定
/////////////////////////////////////////////////////////////////
//電子のエネルギー
double E1 = 0.25 * eV;
double E2 = 1.0 * eV;
double E3 = 4.0 * eV;
//波数
double k1 = sqrt(2.0 * me * E1 / (hbar*hbar));
double k2 = sqrt(2.0 * me * E2 / (hbar*hbar));
double k3 = sqrt(2.0 * me * E3 / (hbar*hbar));
//角振動数
double omega1 = E1 / hbar;
double omega2 = E2 / hbar;
double omega3 = E3 / hbar;
//時間間隔
double dt = 1E-16;
//空間刻み間隔
double dx = 1E-10;
int XN = 400;
int TN = 1000;
double x_min = -20.0;
double x_max = 20.0;
/////////////////////////////////////////////////////////////////
int main() {
std::cout << 2.0*M_PI / omega2 << " " << 2.0*M_PI / k2 << std::endl;
//出力ストリームによるファイルオープン
std::ofstream fout;
fout.open("wave.txt");
fout << "#x:位置" << std::endl;
fout << "#y:波動関数の実部" << std::endl;
fout << "#showLines: true true true" << std::endl;
fout << "#showMarkers: false false false" << std::endl;
fout << "#xrange:" << x_min << " " << x_max << " " << 2 << std::endl;
fout << "#yrange:" << -1.2 << " " << 1.2 << " " << 0.2 << std::endl;
//各時刻における計算を行う
for (int tn = 0; tn < TN; tn++) {
double t = dt * tn;
std::cout << tn << std::endl;
fout << "#coma:" << tn << std::endl;
for (int ix = 0; ix <= XN; ix++) {
double x = (x_min + (x_max - x_min) * ix / XN) * dx;
double psi1 = cos(k1 * x - omega1 * t);
double psi2 = cos(k2 * x - omega2 * t);
double psi3 = cos(k3 * x - omega3 * t);
fout << x / dx << " " << psi1 << " " << psi2 << " " << psi3 << std::endl;
}
fout << std::endl;
}
fout.close();
}