タグ: 量子力学

あとで、電磁波（古典）による「光電効果」（束縛状態の電子が外場によって非束縛状態へ遷移する効果）をシミュレーションしたいので、その準備として、水素原子に束縛された固有状態のフーリエ変換を数値的に調べておくよ。$ \boldsymbol{k} = \frac{2\pi}{L}(n_x, n_y, n_z) $ で、$L$ は空間サイズで $V =L^3$、 $n_x, n_y, n_z$ は整数として、固有状態の波数成分 $\varphi_{nlm}( \boldsymbol{k} )$ は、

\begin{align}
\varphi_{nlm}( \boldsymbol{k} ) = \frac{1}{\sqrt{V}} \int \varphi_{nlm}( \boldsymbol{r} ) e^{-i \boldsymbol{k} \cdot \boldsymbol{r} }dV
\end{align}

で表すことができるね。とりあえず、基底状態 $\varphi_{100}( \boldsymbol{k} ) $ の波数空間分布を示すよ（ $\varphi_{100}( \boldsymbol{k} ) $ の $kx-ky$ 平面上の値を、大きさは不透明度、位相は色で表しているよ）。

磁場中の電子に対するスピン自由度を含めた波動関数 $\Psi(\boldsymbol{r}, t)$ は、シュレーディンガー方程式から導かれるパウリの方程式と呼ばれる

\begin{align}
i\hbar \frac{\partial \Psi(\boldsymbol{r}, t)}{\partial t} = \left[ \frac{1}{2m_e} (-i\hbar\nabla + e\boldsymbol{A})^2 + V(r) + \frac{e}{m_e} \hat{\boldsymbol{S}} \cdot \boldsymbol{B} \right] \Psi(\boldsymbol{r}, t)
\end{align}

を満たすね。この方程式を満たす波動関数は空間依存部分 $\psi(\boldsymbol{r}, t)$ とスピン依存部分 $\chi(t)$ に分離して、$\Psi(\boldsymbol{r}, t)=\psi(\boldsymbol{r}, t)\chi(t)$ と表わすことで、方程式は変数分離できるね。

\begin{align}
i\hbar \frac{\partial \psi(\boldsymbol{r}, t)}{\partial t} &\, = \left[ \frac{1}{2m_e} (-i\hbar\nabla + e\boldsymbol{A})^2 + V(r) \right] \psi(\boldsymbol{r}, t)\\
i\hbar \frac{d \chi( t )}{d t} &\, = \frac{e}{m_e}\, \hat{\boldsymbol{S}} \cdot \boldsymbol{B}\, \chi(\boldsymbol{r}, t)
\end{align}

このスピン依存部分は、スピン角運動量 $\boldsymbol{S} = (S_x, S_y, S_z)$ をパウリ行列

\begin{align}
S_x = \frac{\hbar}{2} \left( \matrix{ 0 & 1 \cr 1 & 0} \right) \ , \ S_y = \frac{\hbar}{2} \left( \matrix{ 0 & -i \cr 1 & 0} \right)\ , \ S_z = \frac{\hbar}{2} \left( \matrix{ 1 & 0 \cr 0 & -1} \right)
\end{align}

で表したときのスピノールと呼ばれる縦ベクトルで表すことができるね。スピノールを

\begin{align}
\chi( t ) = \left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right)
\end{align}

と表しておいて、パウリ方程式に代入して、$\chi_{\uparrow}(t)$ と $\chi_{\downarrow}(t)$ の時間依存性を計算することができるね。

静磁場中のスピノールの時間依存性

まずは、静磁場を $\boldsymbol{B} = (0, 0, B_z)$ として、静磁場中のスピノールの時間依存性を計算してみよう。パウリ方程式のスピン部分は

\begin{align}
i\hbar \frac{d }{d t} \left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) &\ = \frac{e\hbar B_z}{2m_e}\, \left( \matrix{ 1 & 0 \cr 0 & -1} \right) \left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) \\
&\ = \frac{e\hbar B_z}{2m_e}\,\left( \matrix{ \chi_{\uparrow}(t) \cr – \chi_{\downarrow}(t)} \right)
\end{align}

となるね。これは直ちに解くことができて、

\begin{align}
\chi( t ) = \left( \matrix{\chi_{\uparrow}(0) e^{-i\omega_L t} \cr \chi_{\downarrow}(0) e^{i\omega_L t}} \right) \ , \ \omega_L = \frac{e B_z}{2m_e}
\end{align}

となるね。$ |\chi( t )|^2 = |\chi( 0 )|^2 $ を満たすから、時間が経っても初期状態から変化しないことが分かるね。

振動磁場中のスピノールの時間依存性

次は、時間依存する磁場を $\boldsymbol{B}(t) = (0, 0, B_z\cos(\omega t))$ として、振動磁場中のスピノールの時間依存性を計算してみよう。パウリ方程式のスピン部分は

\begin{align}
i\hbar \frac{d }{d t} \left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) &\ = \frac{e\hbar B_z\cos(\omega t)}{2m_e}\,
\left( \matrix{ 1 & 0 \cr 0 & -1} \right) \left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) \\
&\ = \frac{e\hbar B_z\cos(\omega t)}{2m_e}\,\left( \matrix{ \chi_{\uparrow}(t) \cr – \chi_{\downarrow}(t)} \right)
\end{align}

となるね。これも直ちに解くことができて、

\begin{align}
\chi( t ) = \left( \matrix{\chi_{\uparrow}(0) e^{-i\frac{\omega_L}{\omega} \sin(\omega t)} \cr \chi_{\downarrow}(0) e^{i\frac{\omega_L}{\omega} \sin(\omega t)}} \right) \ , \
\omega_L = \frac{e B_z}{2m_e}
\end{align}

となるね。振動磁場を与えても $ |\chi( t )|^2 = |\chi( 0 )|^2 $ を満たすから、時間が経っても初期状態から変化しないことが分かるね。

静磁場に垂直方向の振動磁場を加えたときのスピノールの時間依存性

今度は、時間依存する磁場を $\boldsymbol{B}(t) = (0, B_y\sin(\omega t), B_z)$ として、振動磁場中のスピノールの時間依存性を計算してみよう。パウリ方程式のスピン部分は

\begin{align}
i\hbar \frac{d }{d t} \left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) &\ =\frac{e\hbar }{2m_e}\left[B_y\sin(\omega t)\left( \matrix{ 0 & -i \cr i & 0} \right) + B_z\left( \matrix{ 1 & 0 \cr 0 & -1} \right)\right]
\left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) \\
&\ =\frac{e\hbar }{2m_e}\left( \matrix{ B_z& -iB_y\sin(\omega t) \cr iB_y\sin(\omega t) & -B_z} \right) \left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) \\
&\ = \frac{e\hbar }{2m_e}\,\left( \matrix{ B_z\chi_{\uparrow}(t)-iB_y\sin(\omega t)\chi_{\downarrow}(t) \cr iB_y\sin(\omega t) \chi_{\uparrow}(t) -B_z\chi_{\downarrow}(t)} \right)
\end{align}

と、 $\chi_{\uparrow}(t)$ と $\chi_{\downarrow}(t)$ に関する連立微分方程式が得られるね。解析的に解けるかはわからないけれども、数値的に解くことで、スピノールの時間依存性を計算することができそうだね。異常ゼーマン効果で分かれる２つの準位間のエネルギーに相当する振動磁場（電磁波）の角振動数を与えると、共鳴が起こってスピンの向きが変わるね。これは磁気共鳴現象って呼ばれるよ。これを次回の課題にするね。

円偏光を入射したときのスピノールの時間依存性

最後に、時間依存する磁場を $\boldsymbol{B}(t) = (0, B_0\sin(\omega t), B_0\cos(\omega t))$ として、円偏光を入射したときのスピノールの時間依存性を計算してみよう。パウリ方程式のスピン部分は

\begin{align}
i\hbar \frac{d }{d t} \left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) &\ =\frac{e\hbar }{2m_e}\left[B_y\left( \matrix{ 0 & -i \cr i & 0} \right) + B_z\cos(\omega t)\left( \matrix{ 1 & 0 \cr 0 & -1} \right)\right]
\left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) \\
&\ =\frac{e\hbar }{2m_e}\left( \matrix{ B_z\cos(\omega t) & -iB_y \cr iB_y & -B_z\cos(\omega t)} \right) \left( \matrix{\chi_{\uparrow}(t) \cr \chi_{\downarrow}(t)} \right) \\
&\ = \frac{e\hbar }{2m_e}\,\left( \matrix{ B_z\cos(\omega t)\chi_{\uparrow}(t)-iB_y\chi_{\downarrow}(t) \cr iB_y \chi_{\uparrow}(t) -B_z\cos(\omega t)\chi_{\downarrow}(t)} \right)
\end{align}

と、 $\chi_{\uparrow}(t)$ と $\chi_{\downarrow}(t)$ に関する連立微分方程式が得られるね。解析的に解けるかはわからないけれども、数値的に解くことで、スピノールの時間依存性を計算することができそうだね。円偏光でもスピンの向きは変化しそうだね。これも次回の課題にするね。

以前解説したハミルトニアンを用いて、水素原子の基底状態の電子に電磁波（古典・直線偏光）を入射したの様子をシミュレーションしたよ。結果を示すね。

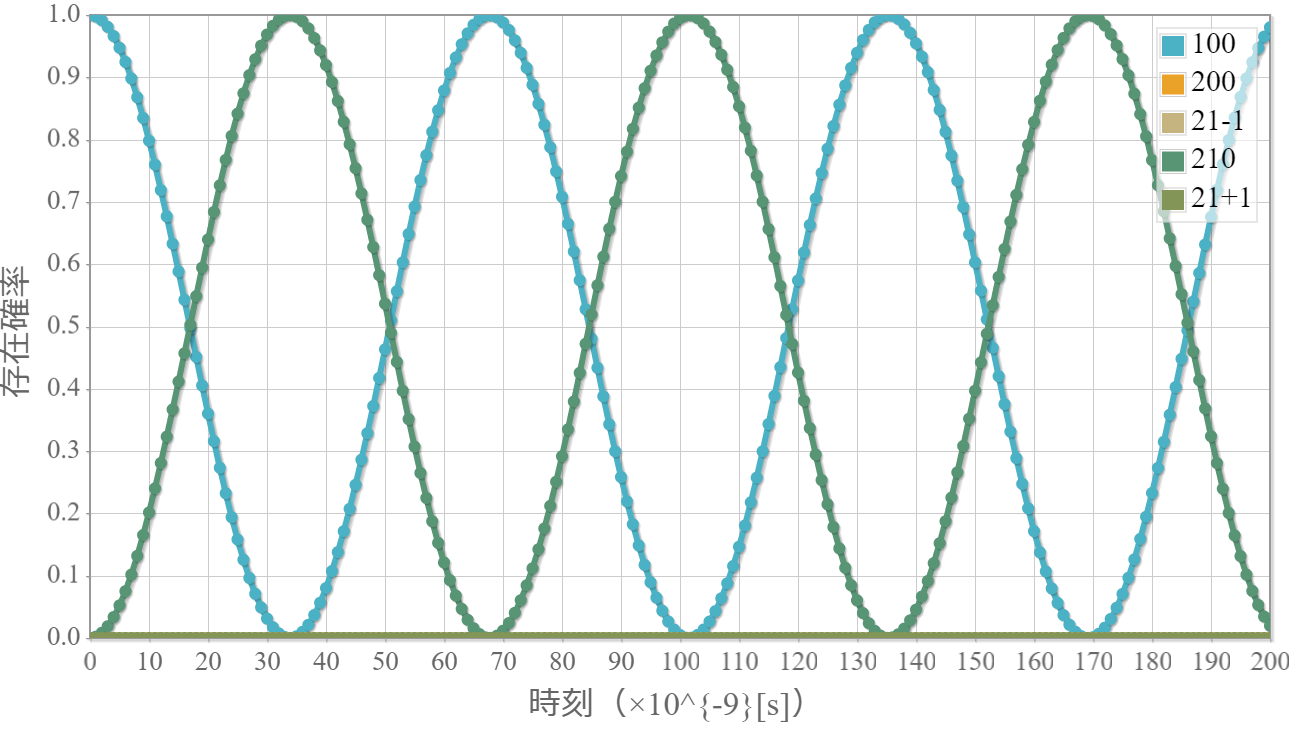
角振動数 $\omega_{12} = (E_2-E_1)/\hbar$ の電磁波を入射

次のグラフは、基底状態と第１励起状態のエネルギー準位の差に対応する電磁波を入射した結果だよ。$ \varphi_{100} $ と $ \varphi_{210} $ の間でラビ振動している様子が分かるね。

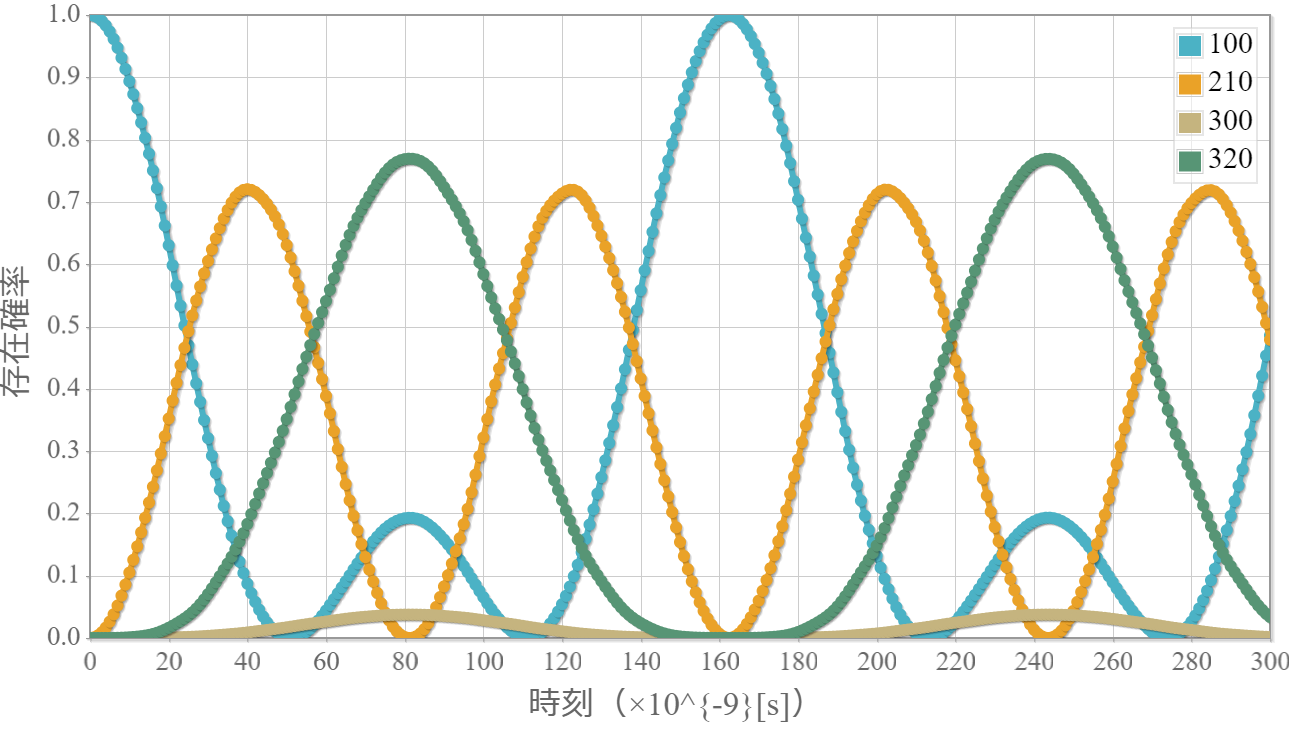
角振動数 $\omega_{12} = (E_2-E_1)/\hbar$ と $\omega_{23} = (E_3-E_2)/\hbar$の電磁波を入射

次のグラフは、基底状態と第１励起状態のエネルギー準位の差に対応する電磁波と、第１励起状態と第２励起状態ののエネルギー準位の差に対応する電磁波を同時に入射した結果だよ。$ \varphi_{100} $ と $ \varphi_{210} $ に加えて、$ \varphi_{100} $ から直接遷移することができない $ \varphi_{300} $ と $ \varphi_{320} $ にも励起しているね。このように、直接遷移が許されない状態が加わっても、存在確率が周期的に振動するのはちょっと意外だね。

次回は、円偏光の電磁波を入射するよ。

前回解説した水素原子に静電場を急激に加えたときの緩和時間シミュレーションの結果を示すよ。次の図は初期状態として $\varphi_{200}$ 100%の状態に $ E_z = 10^{9}[\rm{V/m}]$ の静電場を急に加えたときの $\varphi_{200}$ と $\varphi_{210}$ の存在確率の時間経過だよ。$\varphi_{200}$ 100%の状態と $\varphi_{210}$ 100%の状態が一定の周期で交互に現れるね。

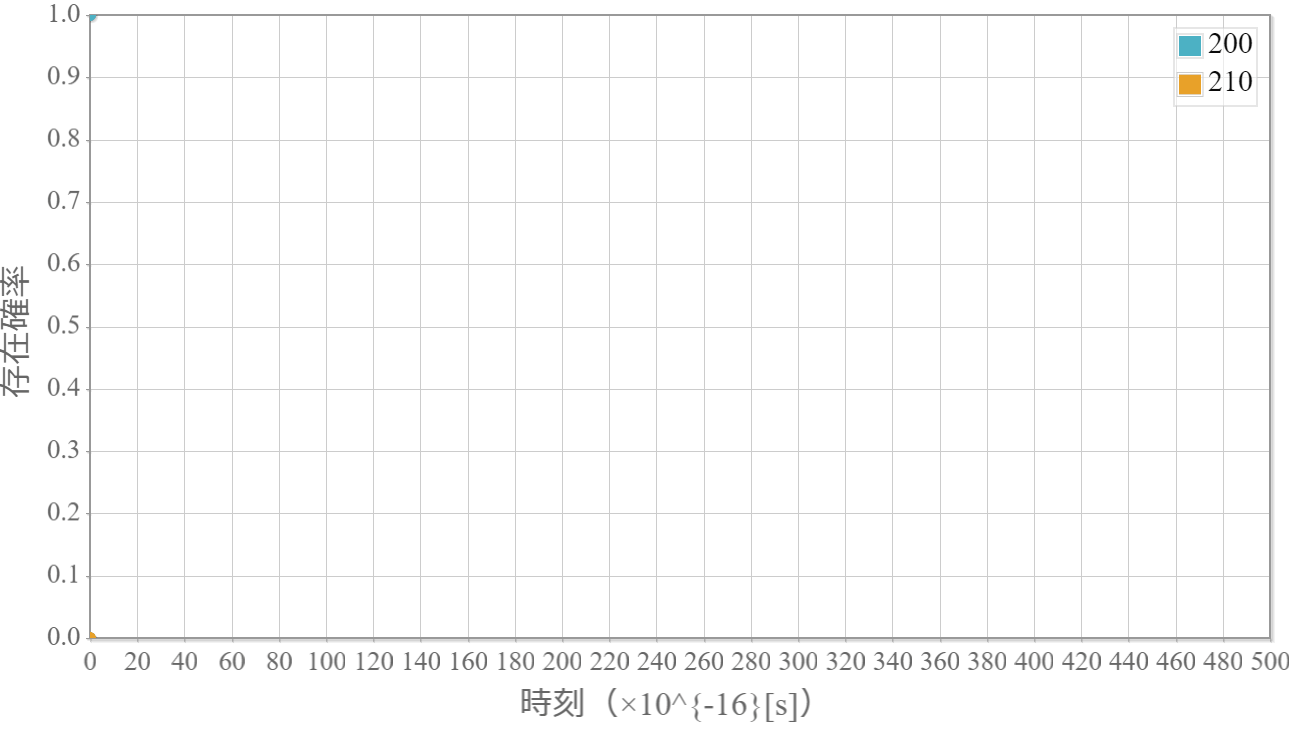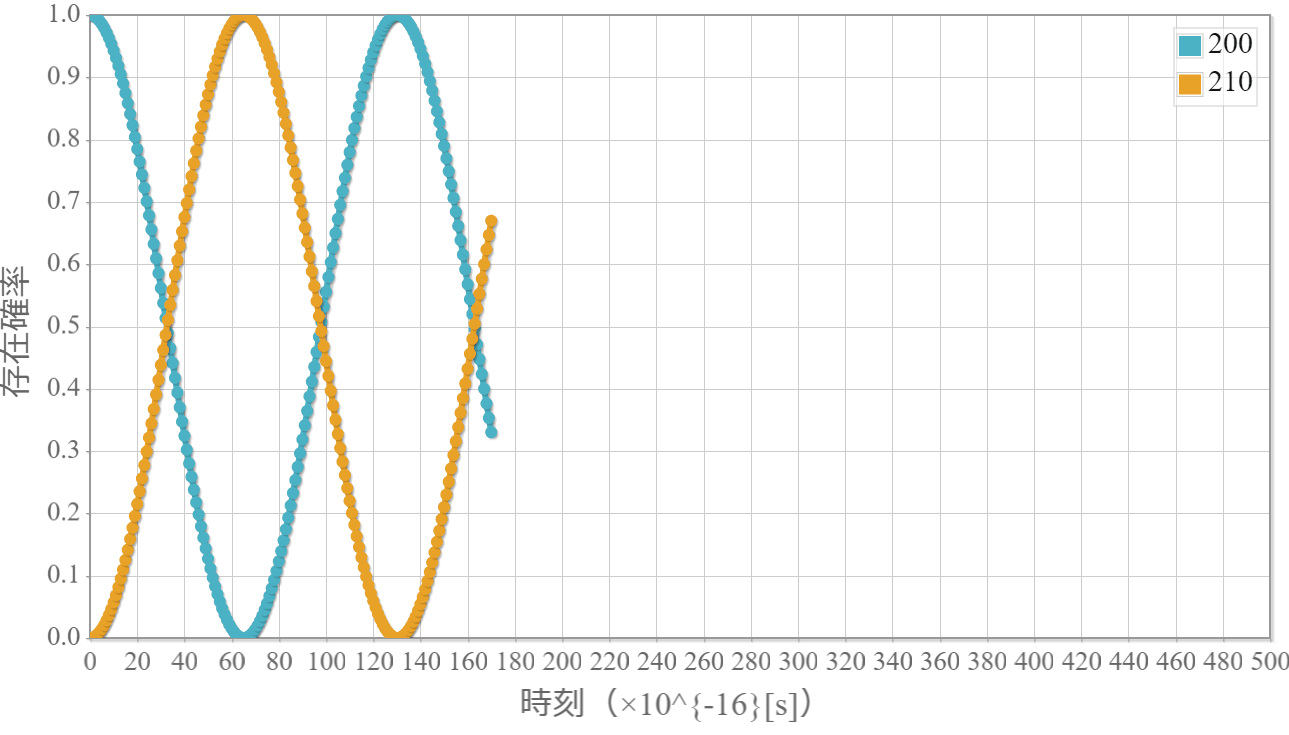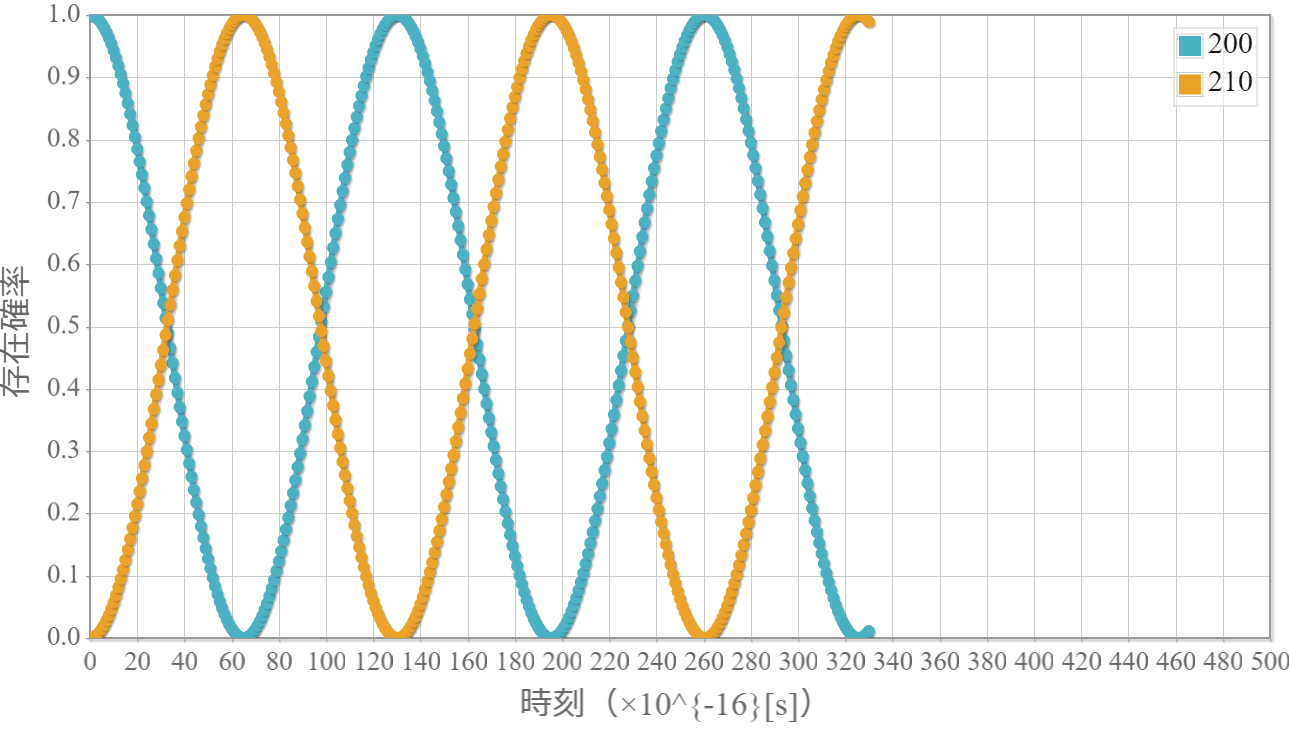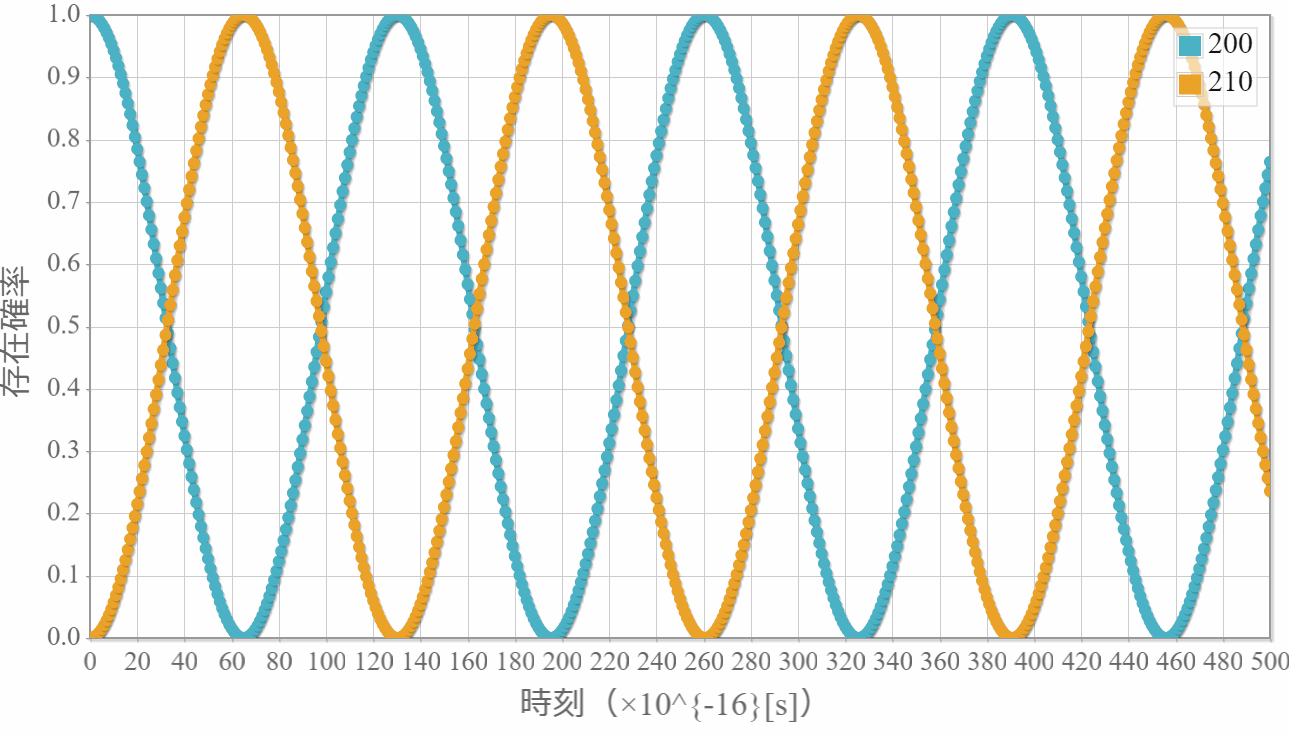
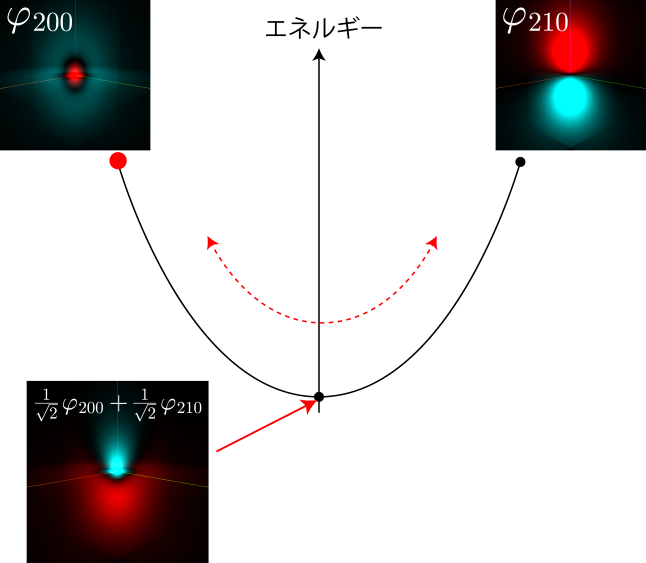
考察：単振動的な運動をする理由

$\varphi_{200}$ と $\varphi_{210}$ は静電場中ではエネルギーが高い一方で、その50%づつの混合状態が一番エネルギーが低いのだよね。つまり、下の図で示したとおり、エネルギーの高い初期状態 $\varphi_{200}$ 100% からスタートして、エネルギー低い方に状態が変化して行くけれども、一番低いところで止まらずに反対の $\varphi_{210}$ 100% の状態まで変化していっているね。もし、エネルギーが散逸するメカニズムがあれば、最低エネルギーに落ち着くよね。きっと。

はじめに少し復習するよ。
スピン―軌道相互作用を考慮した水素原子のハミルトニアンは

\begin{align}
\hat{H} = \hat{H}_0 + \frac{e^2}{8\pi \epsilon_0 c^2 r^3 m_e^2 }\,\hat{\boldsymbol{L}}\cdot\hat{\boldsymbol{S}}
\end{align}

だね。このハミルトニアンのエネルギー固有状態となる固有関数は、軌道角運動量とスピン角運動量を合成して生成した $\varphi_{n,l,j,m_j}$ だね。この場合の固有エネルギーは

\begin{align}
E = E_n + \frac{\hbar^2e^2}{16\pi \epsilon_0 c^2 r^3 m_e^2 }\left[ j(j+1) – l(l+1) – \frac{3}{4} \right] \int
\varphi_{nljm_j}^*\,\frac{1}{r^3}\, \varphi_{nljm_j} dV
\end{align}

だったね。これにさらに外部から磁場を加えると、ハミルトニアンに次のように表せるね。

\begin{align}
\hat{H} = \hat{H}_0 + \frac{e^2}{8\pi \epsilon_0 c^2 r^3 m_e^2 }\,\hat{\boldsymbol{L}}\cdot\hat{\boldsymbol{S}} + \frac{eB_z}{2m_e} \left(\hat{L}_z+2\hat{S}_z\right) + \frac{e^2B_z^2}{8m_e} (x^2 + y^2)
\end{align}

このハミルトニアンに現れるゼーマン項の $\hat{L}_z$ と $\hat{S}_z$ はどちらも、先の固有関数 $\varphi_{nljm_j} $ では固有状態にならいんだよね。つまり、このハミルトニアンはたとえ最後の項を無視したとしても、解析的には固有状態を得られそうにないね。これまでと同様の手順で、固有状態をシミュレーションしてみよう！

新しい固有状態を $\varphi_{nljm_j}$ で展開しよう！

先のハミルトニアン $\hat{H}$ の固有関数 $\Psi$ を 軌道角運動量とスピン角運動量を合成して生成した $\varphi_{nljm_j}$ で展開しよう。

\begin{align}
\Psi = \sum\limits_{n, l , j, m_j} a_{nljm_j}\varphi_{nljm_j}
\end{align}

ただし、$n, l, j, m_j$ の範囲は次のとおりだよ。

\begin{align}
0 \le &\ l < n \\ \left|l - \frac{1}{2}\right| \le &\ j \le l + \frac{1}{2} \\ -\left(\le l + \frac{1}{2}\right) \le &\ m_j \le l + \frac{1}{2} \end{align}

シュレーディンガー方程式 $\hat{H}\psi = E\psi $ に代入して、展開係数を決定する方程式を導出しよう。ハミルトニアンを次のように対角成分 $H_0$ と非対角成分を含む $\hat{H}’$ に分けて、$\hat{H} = \hat{H}_0 + \hat{H}’$ と記述すると、シュレーディンガー方程式は次の用になるね。

\begin{align}
\sum\limits_{n, l , j, m_j} (E_n + \hat{H}’) a_{nljm_j}\varphi_{nljm_j} = E \sum\limits_{n, l , j, m_j} a_{nljm_j}\varphi_{nljm_j}
\end{align}

両辺に $\varphi^*_{n’l’j’m’_j}$ を掛けて、全空間で空間積分すると、展開係数 $a_{njlm_j}$ に関する連立方程式が得られるね。

\begin{align}
E_{n’} a_{n’l’j’m’_j} + \sum\limits_{n, l , j, m_j} a_{nljm_j} \int \varphi^*_{n’l’j’m’_j}\hat{H}’ \varphi_{nljm_j} dV = E
a_{n’l’j’m’_j}
\end{align}

あとは、これを連立方程式を数値的に解くだけだね。