投稿者: simu-kun

ディラックのデルタ関数は次の２式でされる超関数だね。

\begin{align}
\int _{-\infty}^{\infty}f(x)\delta(x)dx=f(0) \ \ \ , \ \ \ \int _{-\infty}^{\infty}\delta(x)dx=1
\end{align}

一方、ヘビサイト関数（ステップ関数）は

\begin{align}
\sigma(x) = \left\{ \matrix{ 1 & \cdots & x>0 \cr 0 & \cdots & x<0 } \right. \end{align}

で定義される不連続な関数だけれども、このヘビサイト関数の導関数 $d\sigma'(x) =\sigma/dx$ はディラックのデルタ関数と一致するよ。

証明

ヘビサイト関数の導関数 $d\sigma'(x)$ がディラックのデルタ関数の定義式を満たすことを示すよ。

\begin{align}
\int _{-\infty}^{\infty}f(x)\sigma'(x)dx=f(0) \ \ \ , \ \ \ \int _{-\infty}^{\infty}\sigma'(x)dx=1
\end{align}

まず第２式からだけれどもこれはほぼ自明だね。

\begin{align}
\int _{-\infty}^{\infty}\sigma'(x)dx = \left[\sigma(x)\right]_{-\infty}^\infty = 1
\end{align}

次に第２式だけれども、積分区間を極限操作を用いて有限区間に置き換えておくことで計算することができるね。

\begin{align}
\int _{-\infty}^{\infty}f(x)\sigma'(x)dx &= \lim\limits_{\epsilon\to \infty} \int _{-\epsilon}^{\epsilon}f(x)\sigma'(x)dx = \lim\limits_{\epsilon\to \infty} \left\{ \left[f(x)\sigma(x)\right]_{-\epsilon}^\epsilon – \int_{-\epsilon}^{\epsilon}f'(x)\sigma(x) dx \right\}\\
& = \lim\limits_{\epsilon\to \infty} \left\{ f(\epsilon) – \int _{0}^{\epsilon}f'(x) dx \right\} = \lim\limits_{\epsilon\to \infty} \left\{ f(\epsilon) – [f(x)]_0^{\epsilon} \right\}\\
& = f(0)
\end{align}

確かにディラックのデルタ関数の定義式を満たすね。つまり、ヘビサイト関数とディラックのデルタ関数は

\begin{align}
\frac{d\sigma(x)}{dx} = \delta(x)
\end{align}

の関係を満たすね。

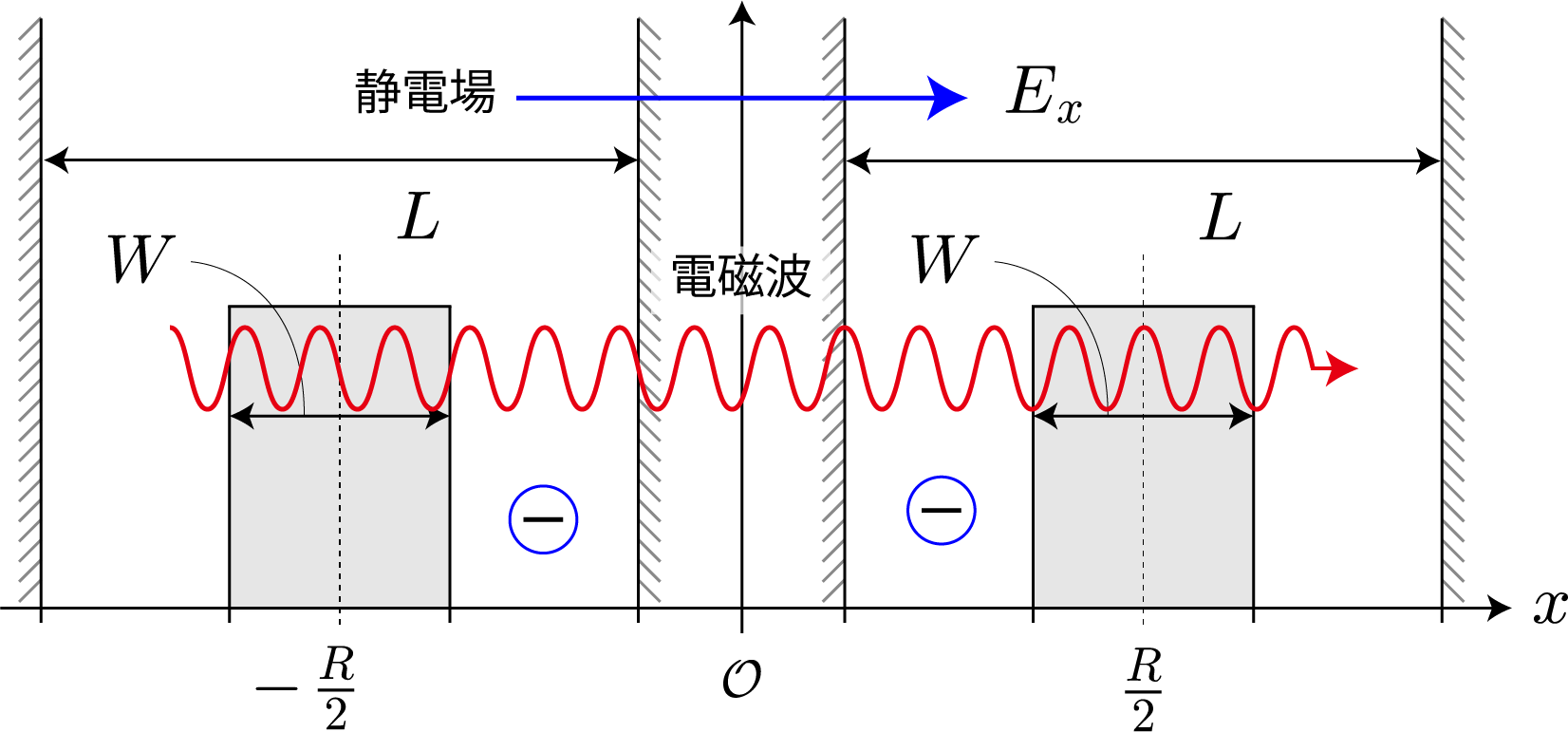
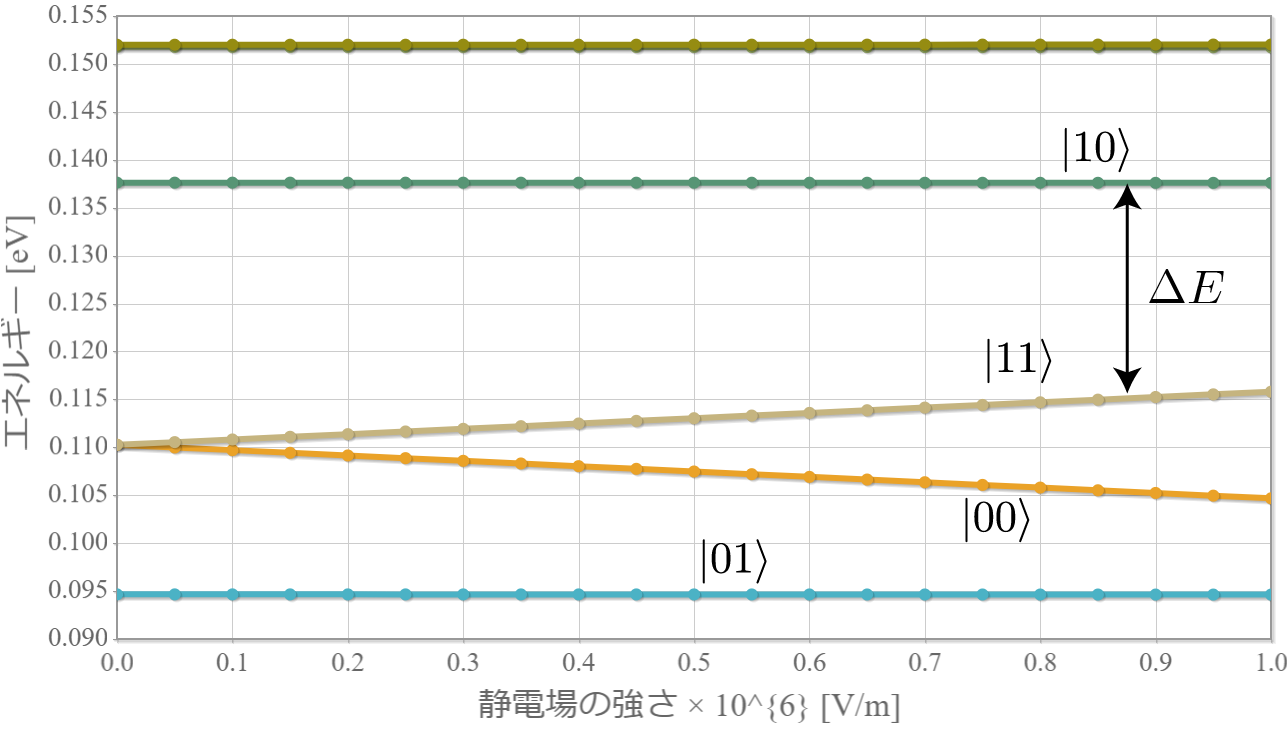
今回は、前回示したハミルトニアン（クーロン相互作用＋静電場＋電磁波）を用いて計算した結果を示すよ。上左図は前々回に示したエネルギー準位の静電場強度依存性だけれども、$|10\rangle$ と $|11\rangle$ のエネルギー差に対応した電磁波を入射して生じる状態遷移を計算するよ。ちなみにこれは、第１量子ビットが $|1\rangle$ のときに第２量子ビットを反転させる制御・NOT演算に対応しているよ。あとで示すけれども、２量子ビットのラビ振動は量子ビット同士が絡み合った量子もつれ（エンタングル）状態を任意に生成することができるよ。

遷移状態：$|10\rangle$ と $|11\rangle$ の存在確率の時間依存性

次のグラフは初期状態 $|10\rangle$ に角振動数 $\omega = \Delta E /\hbar$ の電磁波を入射したときの、$|11\rangle$ との状態遷移の様子だよ。ラビ振動の結果、２つの状態を三角関数的に行ったり来たりするね。$|10\rangle$ 100%の初期状態に約 $ 26.1[{\rm ns}]$ 照射すると、$|10\rangle$ と $|11\rangle$ の存在確率は50%つづとなり、さらに約 $ 26.1[{\rm ns}]$ 照射すると、反対に $|11\rangle$ 100% の状態になるね。ちょうど存在確率が反転する時間の光は「$\pi$パルス」って呼ばれるよ。

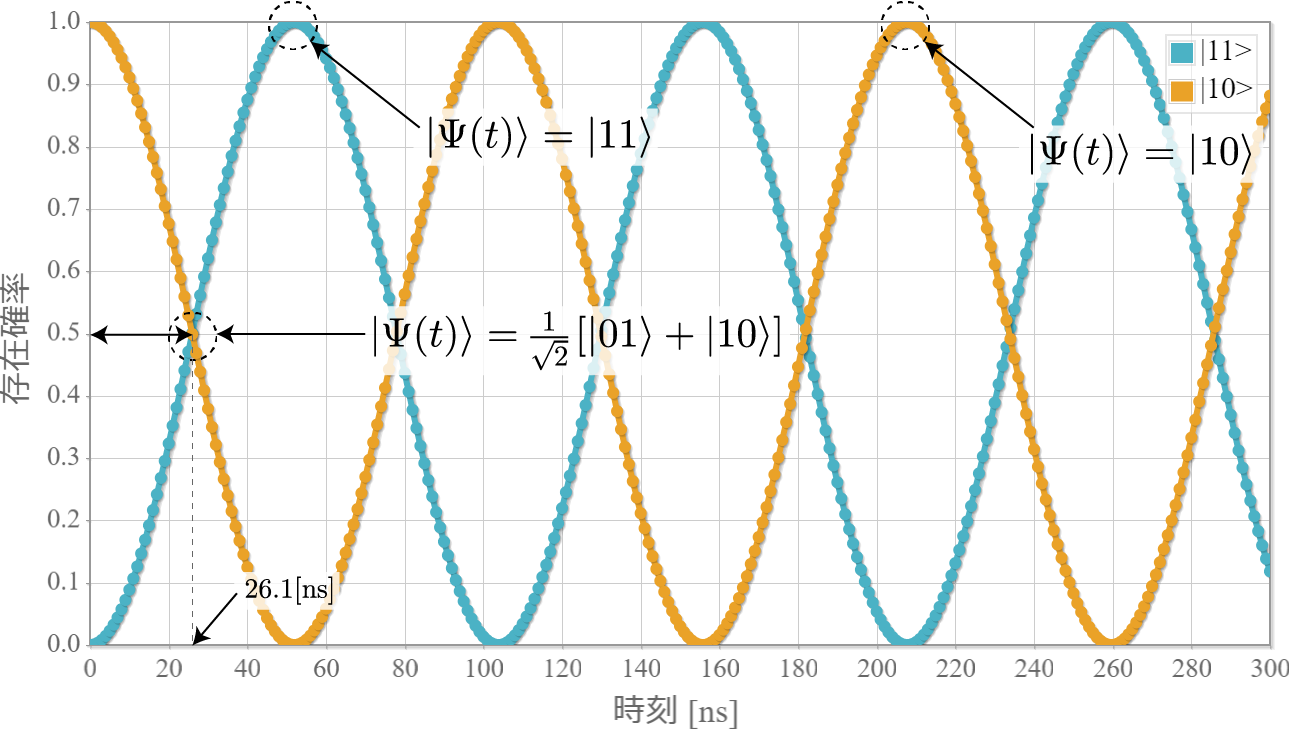
先にも言ったけれども、このラビ振動は２量子ビット同士が絡み合った量子もつれ状態を生み出すことができるね。例えば、$|10\rangle$ と基底状態の $|01\rangle$ のエネルギー差 $\Delta E_{01}^{11}$ として、角振動数 $\omega = \Delta E_{01}^{11} /\hbar$ の電磁波を $\pi$パルスの半分を入射すると、

\begin{align}
|\Psi(t)\rangle = \frac{1}{\sqrt{2}} \left[ |10\rangle + |01\rangle \right]
\end{align}

という状態を作ることができるね。これは単に $|10\rangle$ と $|01\rangle $ の存在確率が 50%づつっていうだけでなくて、第１量子ビットを観測したときに、第２量子を観測しなくてもその状態が100%の確率で分かるという量子もつれ状態となっているよ。具体的には、第１量子ビットが $|0\rangle$ の場合には第２量子ビットは必ず $|1\rangle$ に存在し、また反対に第１量子ビットが $|1\rangle$ の場合には第２量子ビットは必ず $|0\rangle$ に存在するよ。ちなみに、この量子井戸の間隔を量子状態が変化しないようにゆっくりと、どこまで離していっても成り立つよ。そのため、通信に利用することができると考えられているよ。その場合は、量子井戸による量子もつれではなく、光子をを用いた量子もつれを利用するよ。

制御NOT演算に対応する波動関数の時間発展

次の図はラビ振動による制御NOT演算時の波動関数の時間経過を示したアニメーションだよ。左の第１量子井戸は電子が右側（ $|1\rangle$ ）、第２量子井戸は電子が左側（ $|0\rangle$ ）と右側（ $|1\rangle$ ）を行ったり来たりしているね。

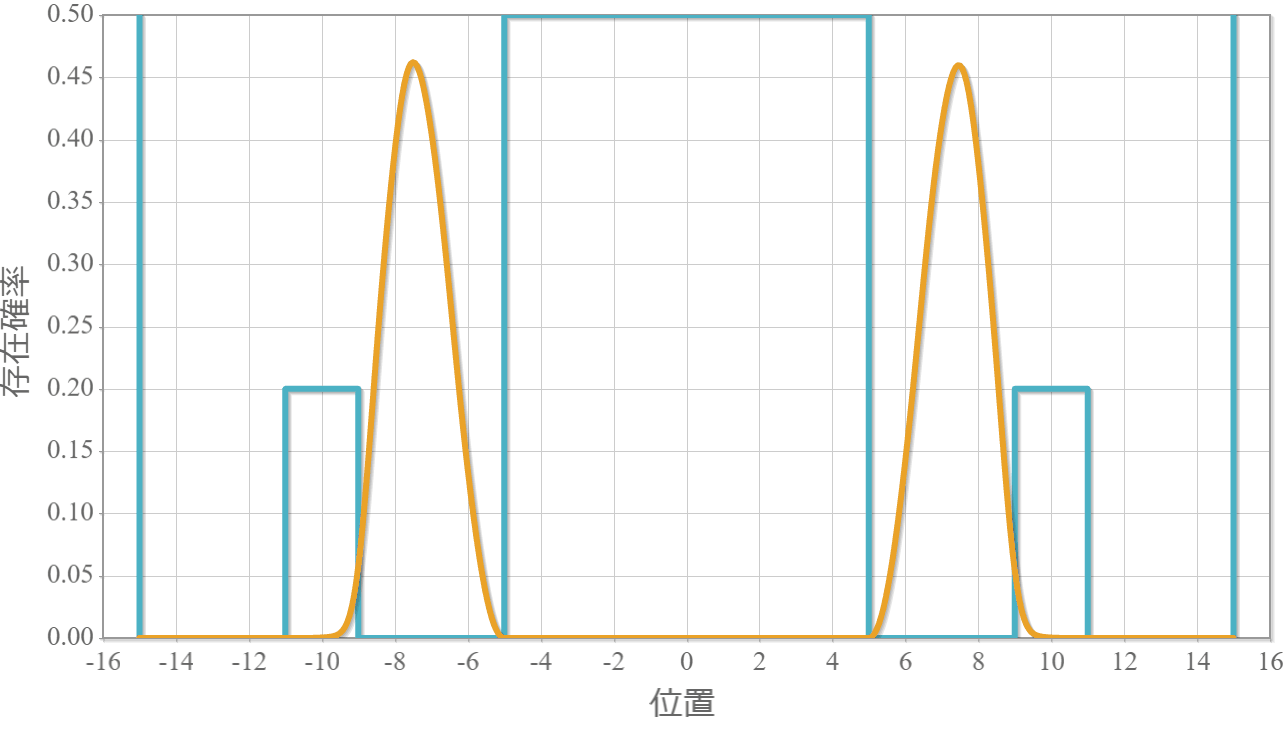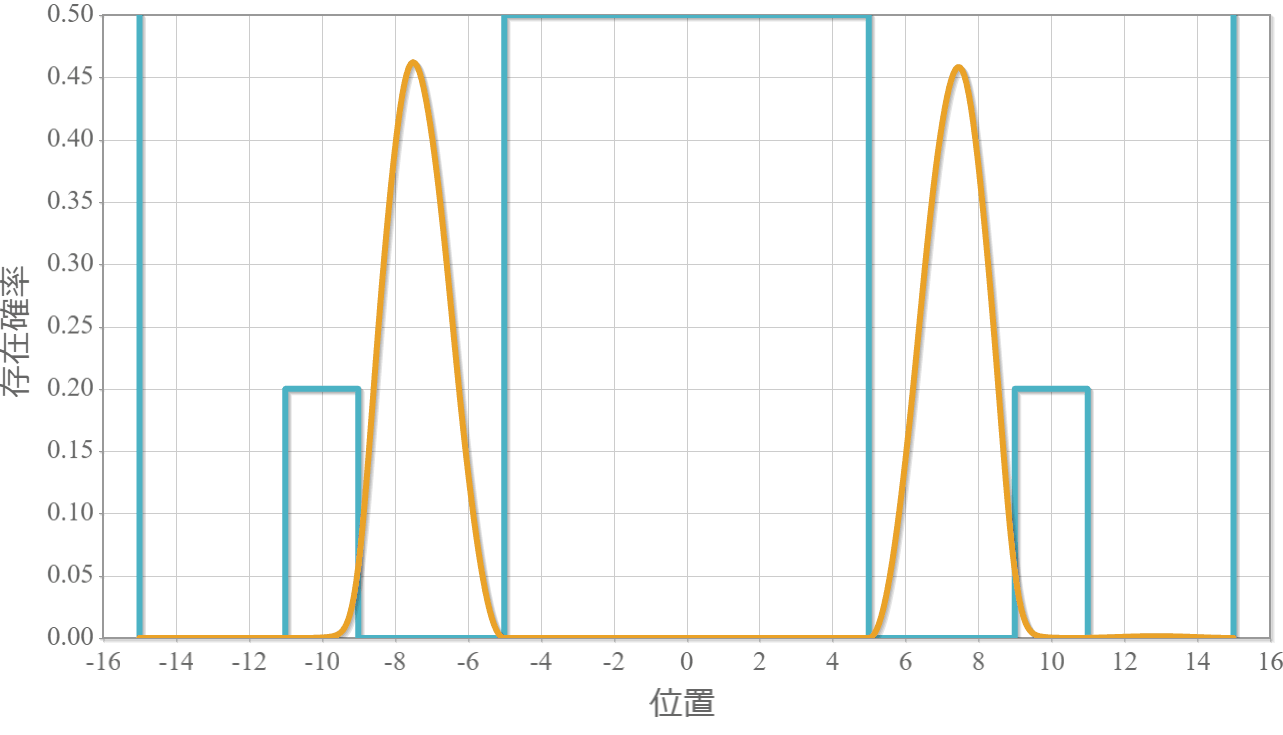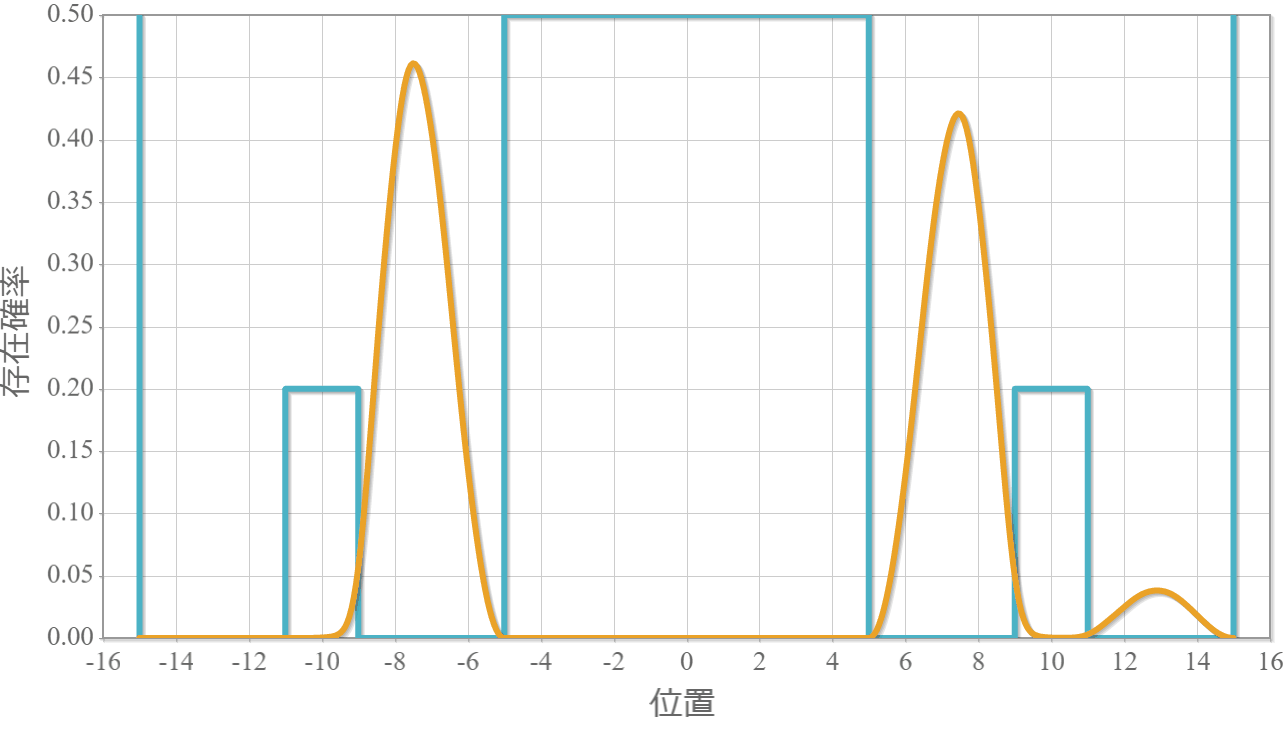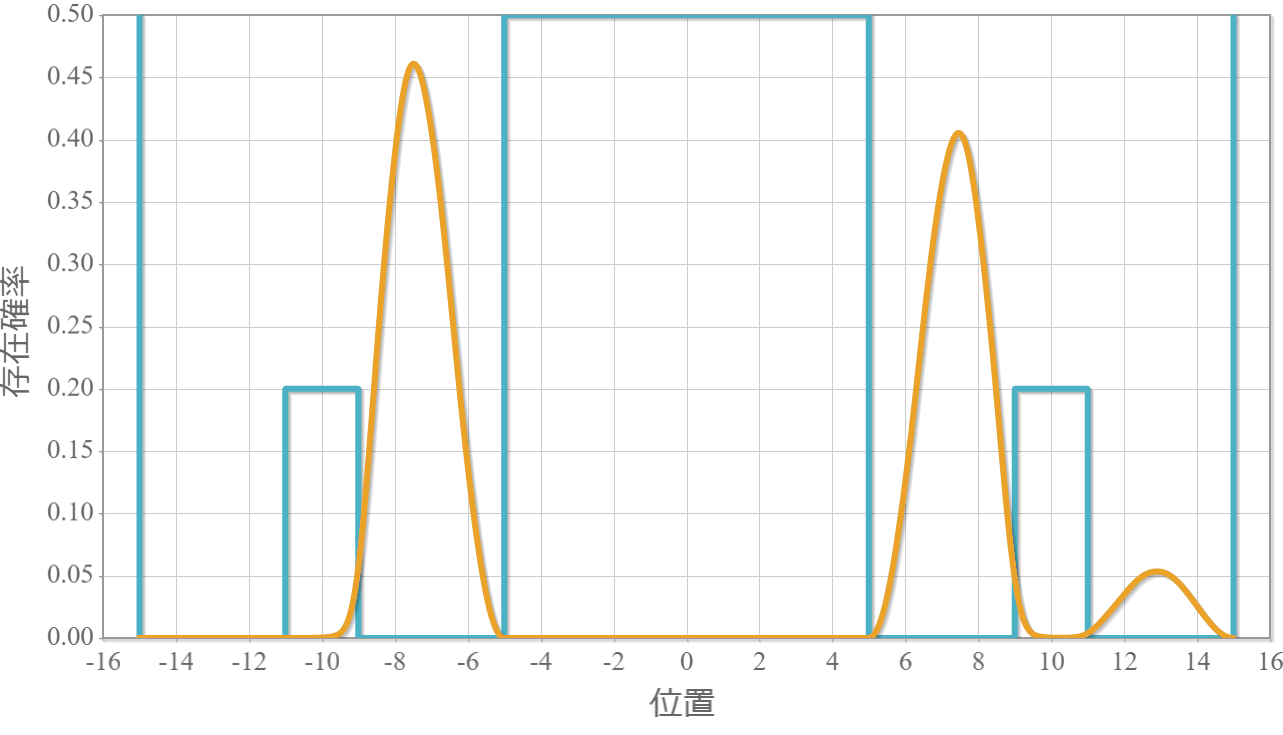
これで量子コンピュータの２量子ビットマシンの動作原理シミュレーションは完成したよ。

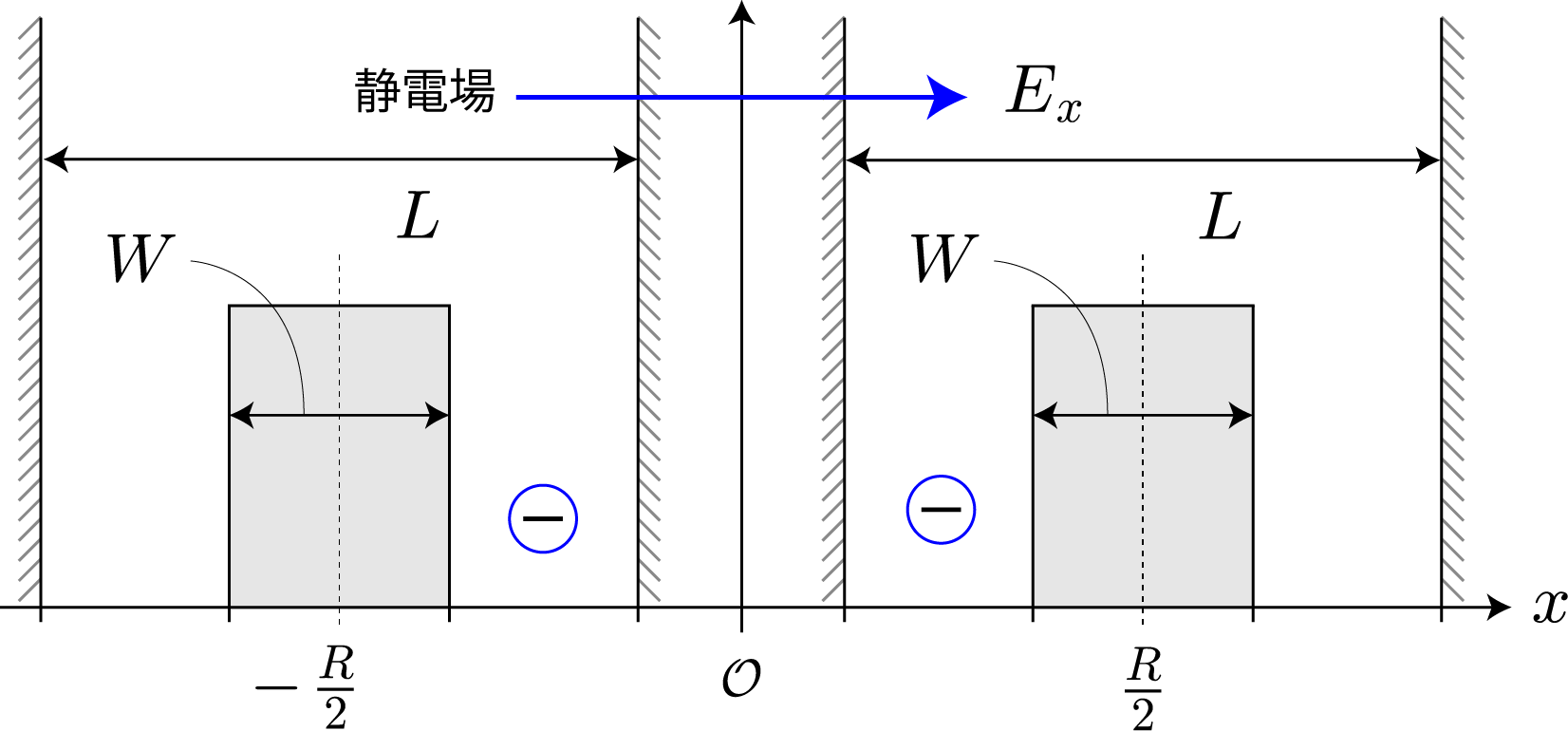
いよいよ最終目的の２量子ビットによる制御NOT演算を行うために、時間発展に必要なハミルトニアンの導出と計算方法を示すよ。復習から入っていくね。量子ビットを表す２つの量子井戸（幅：$L=10[{\rm nm}]$、高さ$+\infty$）はそれぞれが壁（幅： $W=L/5=2[{\rm nm}]$、高さ $V_0=0.3[{\rm eV}]$）で仕切られた２部屋になっていて、前々回と前回解説したとおり、２つの量子井戸の間隔 $R$ がちょうどよければ（$R=20[{\rm nm}]$）、電子間のクーロン相互作用が存在しても、電子は左右のどちらかに存在する状態を作り出せるね。そして、それぞれの量子井戸で左側に電子が存在する状態を $|0\rangle$、右側に電子が存在する場合を $|1\rangle$ と表わして、２電子の状態は $|00\rangle$、$|01\rangle$、$|10\rangle$、$|11\rangle$ の４パターンで表すよ。

定常状態のハミルトニアンと固有関数

この系の固有関数は、２つの量子井戸でそれぞれ定義される関数

\begin{align}
\varphi_{n_1}(x_1) &\ = \sqrt{\frac{2}{L}}\sin\left[ k_{n_1} \left( x_1 + \frac{R}{2} + \frac{L}{2}\right)\right] \ , \
k_{n_1} = \frac{\pi(n_1+1)}{L} \\
\varphi_{n_2}(x_2) &\ = \sqrt{\frac{2}{L}}\sin\left[ k_{n_2} \left( x_2 – \frac{R}{2} + \frac{L}{2}\right)\right] \ , \
k_{n_2} = \frac{\pi(n_2+1)}{L} \\
\end{align}

を用いたその積

\begin{align}
\varphi_{n_1n_2}(x_1, x_2) = \varphi_{n_1}(x_1)\varphi_{n_2}(x_2)
\end{align}

で表される正規直交系で展開することができるね。ちなみに単純な積で表されるのは２つの電子は交わらないからだよ。この２電子系の正規直交関数を用いて、次のように展開することができるね。

\begin{align}
\psi_{l_1l_2}(x_1, x_2) = \sum\limits_{n_1n_2} a^{(l_1l_2)}_{n_1n_2} \varphi_{n_1n_2}(x_1, x_2)
\end{align}

$l_1$ と $l_2$ は $0$ または $1$ のどちらかを取り、$\psi_{00}(x_1, x_2)$ は $|00\rangle$、$\psi_{01}(x_1, x_2)$ は $|01\rangle$、$\psi_{10}(x_1, x_2)$ は $|10\rangle$、$\psi_{11}(x_1, x_2)$ は $|11\rangle$ にそれぞれ対応した固有関数だよ。$a^{(l_1l_2)}_{n_1n_2}$ のように上付きのインデックス $l_1, l_2$ をつけたのはそれぞれの状態で展開係数の値が異なるので明示的につけているよ。この固有関数に対応するハミルトニアンは次のとおりだよ。

\begin{align}
\hat{H}^{(0)} = -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_1^2} + eE_xx_1 + V_1(x_1)-\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_2^2} + eE_xx_2 + V_2(x_2) + \frac{e^2}{4\pi\epsilon_0}\,\frac{1}{|x_1-x_2|}
\end{align}

$\hat{H}^{(0)}$ とインデックスに $(0)$ をつけているのは、前回すでに固有状態を計算できていて、次はこれに電磁波を加えることを想定しているからだよ。先の固有関数はこのハミルトニアンなので固有状態は

\begin{align}
\hat{H}^{(0)}\psi_{l_1l_2}(x_1, x_2) = E^{(0)}_{l_1l_2}\psi_{l_1l_2}(x_1, x_2)
\end{align}

と表されるよ。ここまでが前回の内容だね。ちなみに固有状態は

\begin{align}
\hat{H}^{(0)}|l_1l_2\rangle &\ = E^{(0)}_{l_1l_2}|l_1l_2\rangle \\
\langle l_1l_2| \hat{H}^{(0)} &\ = \langle l_1l_2|E^{(0)}_{l_1l_2}
\end{align}

とも表すことができるよ。これは後で使うね。

電磁波を入射したときのハミルトニアンと計算方法

次に状態遷移を起こすために電磁波を加えるよ。ベクトルポテンシャルを $\boldsymbol{A}(t)$ としてハミルトニアンは

\begin{align}
\hat{H}(t) = \hat{H}^{(0)} + \frac{e}{m_e} \boldsymbol{A}(t)\cdot \hat{\boldsymbol{p}}_1 + \frac{e}{m_e} \boldsymbol{A}(t)\cdot \hat{\boldsymbol{p}}_2
\end{align}

となるね。今回も１次元系で考えているので、ベクトルポテンシャルを$\boldsymbol{A}(t) = (A_x(t), 0, 0)$ として、

\begin{align}
A_{x_1}(t) &\ = A_0 \cos(kx_1-\omega t)\\
A_{x_2}(t) &\ = A_0 \cos(kx_2-\omega t)
\end{align}

なので、ハミルトニアンは

\begin{align}
\hat{H}(t) = \hat{H}^{(0)} + \frac{e}{m_e} A_0 \left[ \cos(kx_1-\omega t)\hat{p}_{x_1} +\cos(kx_2-\omega t)\hat{p}_{x_2} \right]
\end{align}

となるね。このハミルトニアンは時間に依存するので固有状態は存在しないので、波動関数 $\Psi(t,x_1,x_2)$ を先の固有関数 $\psi_{l_1l_2}(x_1, x_2)$ で展開するよ。

\begin{align}
\Psi(t,x_1,x_2) = \sum\limits_{l_1 l_2} b_{l_1l_2}(t) \psi_{l_1l_2}(x_1, x_2)
\end{align}

$b_{l_1l_2}(t)$ が展開係数で、この展開係数が時間とともに変化するよ。時間に依存するシュレーディンガー方程式

\begin{align}
i\hbar \frac{\partial }{\partial t} \Psi(t,x_1,x_2)= \hat{H}(t) \Psi(t,x_1,x_2)
\end{align}

に代入して、両辺に $\psi_{m_1m_2}^*(x_1, x_2)$ を掛けて全空間で積分すると、次のような連立微分方程式になるよ。

\begin{align}
i\hbar \frac{d b_{m_1m_2}(t) }{d t} = E^{(0)}_{m_1m_2} b_{m_1m_2}(t) + e A_0 \sum\limits_{l_1 l_2} b_{l_1l_2}(t) \langle m_1 m_2| \left[\cos(kx_1-\omega t)\frac{\hat{p}_{x_1}}{m_e} + \cos(kx_2-\omega t)\frac{\hat{p}_{x_2}}{m_e}\right]| l_1l_2 \rangle
\end{align}

$\hat{p}_{x_1}/m_e = [\hat{H}^{(0)}, x_1 ]/i\hbar$、 $\hat{p}_{x_2}/m_e = [\hat{H}^{(0)}, x_2 ]/i\hbar$ の恒等式と長波長近似（$kx_1 = kx_2 \simeq 0$）を考慮すると次のようになるよ（特に長波長近似を課すことをしなくても数値計算自体は問題なくできるよ。でも表式が簡単になるね）。

\begin{align}
&\ \langle m_1 m_2| \left[\cos(kx_1-\omega t)\frac{\hat{p}_{x_1}}{m_e} + \cos(kx_2-\omega t)\frac{\hat{p}_{x_2}}{m_e}\right]| l_1l_2 \rangle\\
&\ =\frac{1}{i\hbar} \langle m_1 m_2| \left[\cos(kx_1-\omega t)\left(\hat{H}^{(0)}x_1 – x_1\hat{H}^{(0)}\right) + \cos(kx_2-\omega t)\left(\hat{H}^{(0)}x_2- x_2\hat{H}^{(0)}\right)\right]| l_1l_2 \rangle\\
&\ \simeq \frac{1}{i\hbar}\cos(\omega t)\langle m_1 m_2| \left[\hat{H}^{(0)}x_1 – x_1\hat{H}^{(0)} + \hat{H}^{(0)}x_2- x_2\hat{H}^{(0)}\right]| l_1l_2 \rangle\\
&\ = \frac{1}{i\hbar}\cos(\omega t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right) \langle m_1 m_2|(x_1 + x_2)| l_1l_2
\rangle \\
&\ = \frac{1}{i\hbar}\cos(\omega t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right) \int_{-\frac{R}{2}-\frac{L}{2}}^{-\frac{R}{2}+\frac{L}{2}} dx_1\int_{\frac{R}{2}-\frac{L}{2}}^{\frac{R}{2}+\frac{L}{2}}dx_2 \psi_{m_1m_2}^*(x_1, x_2)(x_1 + x_2)\psi_{l_1l_2}(x_1, x_2)\\
&\ \equiv \frac{1}{i\hbar}\cos(\omega t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right) K^{m_1m_2}_{l_1l_2}
\end{align}

この $K^{m_1m_2}_{l_1l_2}$ は時間に依存しないので１度計算すれば良いね。この $K^{m_1m_2}_{l_1l_2}$ を用いると先の連立微分方程式は次のようになるよ。

\begin{align}
i\hbar \frac{d b_{m_1m_2}(t) }{d t} = E^{(0)}_{m_1m_2} b_{m_1m_2}(t) + \frac{e A_0}{i\hbar} \cos(\omega t)　\sum\limits_{l_1 l_2} b_{l_1l_2}(t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right)K^{m_1m_2}_{l_1l_2}
\end{align}

電磁波の角振動数が２準位間のエネルギー差 $\Delta E = E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2}$ と表して $\omega = \Delta E / \hbar$ となるときに、２準位間を周期的に遷移するね。$\Delta E = E^{(0)}_{11} – E^{(0)}_{10}$ を与えることで、制御・NOT演算となることを次回シミュレーションするよ。

前回、電子同士のクーロン相互作用を考慮した独立した２つの２重量子井戸の電子の固有状態を計算したね。今回はさらに静電場を加えるね。壁の幅と高さは、$W = L/5= 2.0 \times 10^{-9} [{\rm m}] = 2.0[{\rm nm}]$、$V_0 = 3.0[{\rm eV}]$ として、量子井戸の間隔は $R = 20.0[{\rm nm}]$ とするよ。次の結果は、静電場の大きさを $E_x = 0.1\times10^{6}[{\rm V/m}]$ から $1.0\times10^{6}[{\rm V/m}]$ まで $ 0.05\times10^{6}[{\rm V/m}]$ づつ強くしたときの基底状態から第３励起状態までの電子存在確率の空間分布だよ。想定通りだけれども、ちょっとした静電場で第１励起状態と第２励起状態の縮退が解けて、２重量子井戸の壁の左右に分かれる形になったね。それぞれの量子井戸の左に電子がいる状態を $|0\rangle$、右にいる状態を$|1\rangle$　と表すと、それぞれの電子状態は固有エネルギーが低い順番に $|01\rangle, |00\rangle, |10\rangle, |11\rangle$ と表わすことができるね。

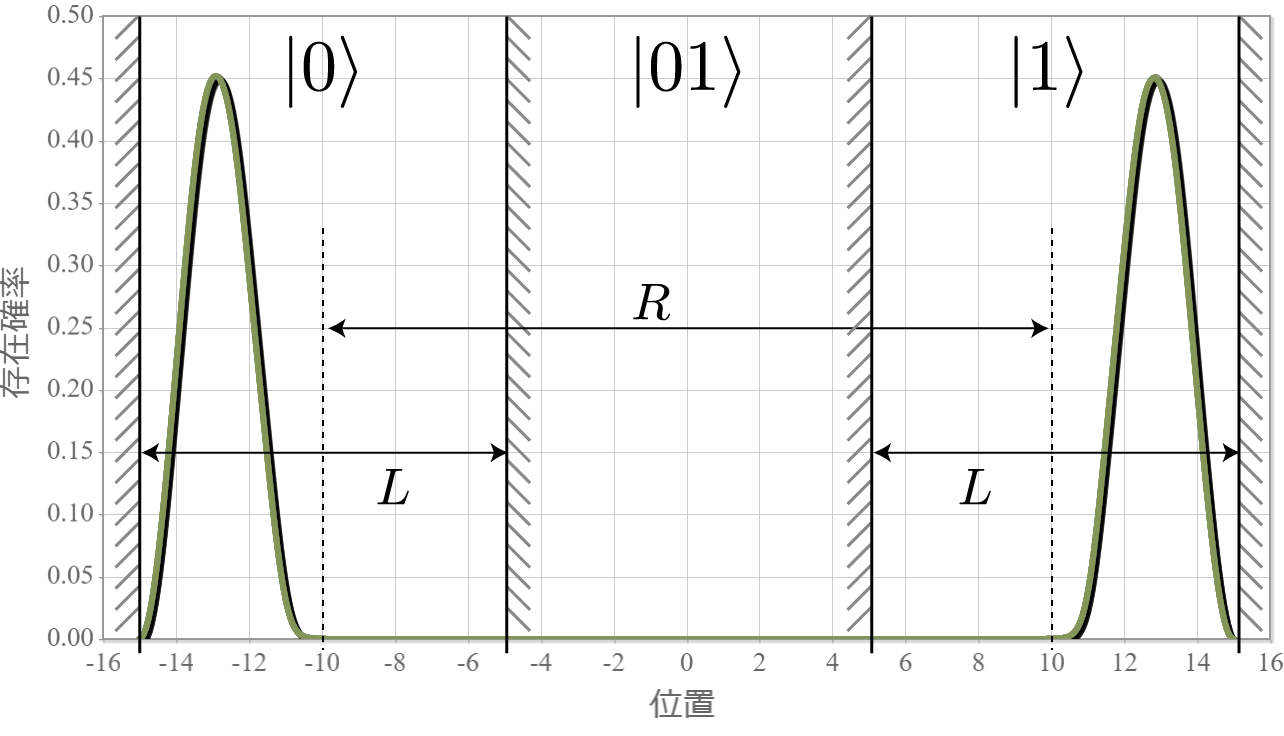
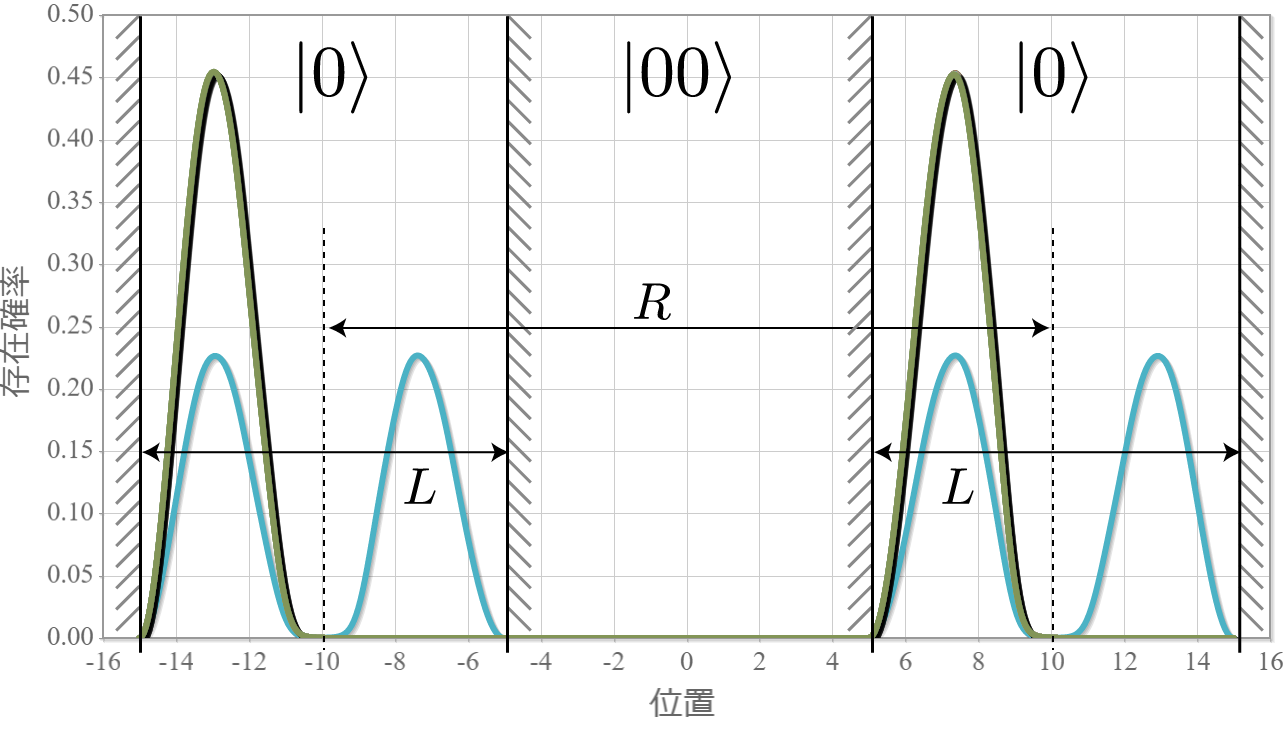
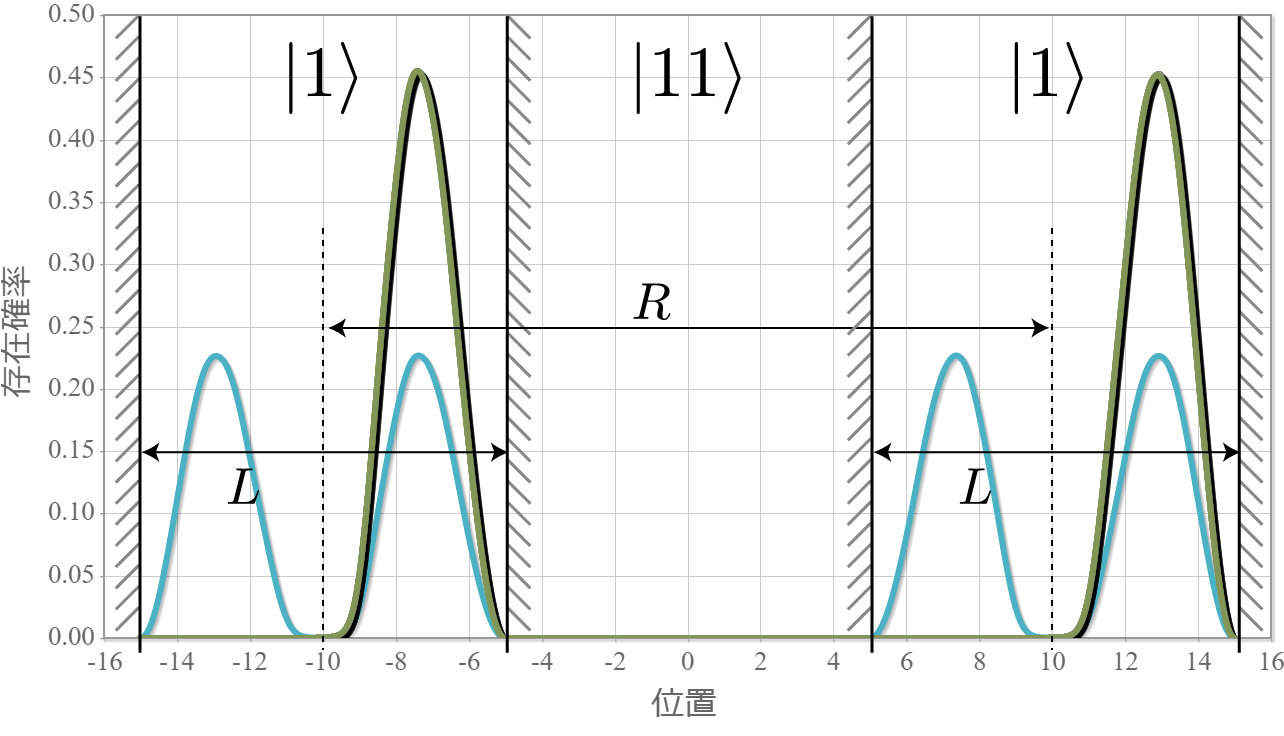
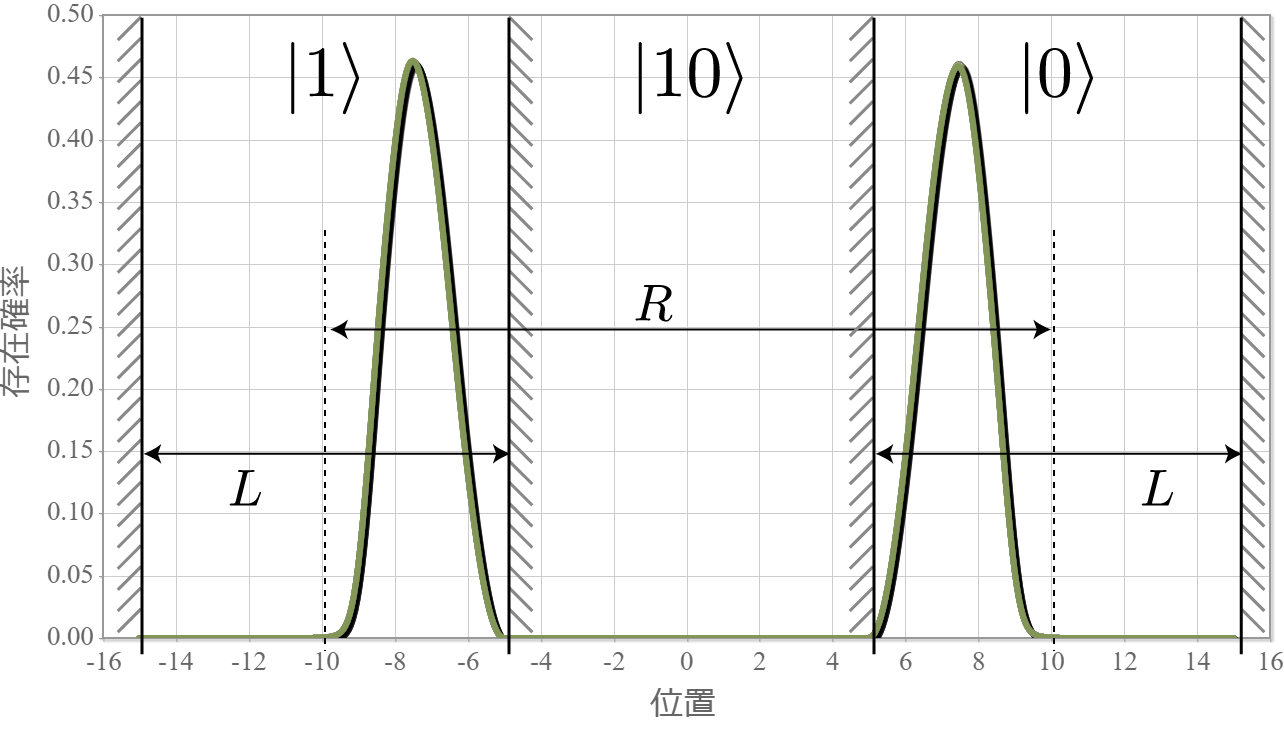
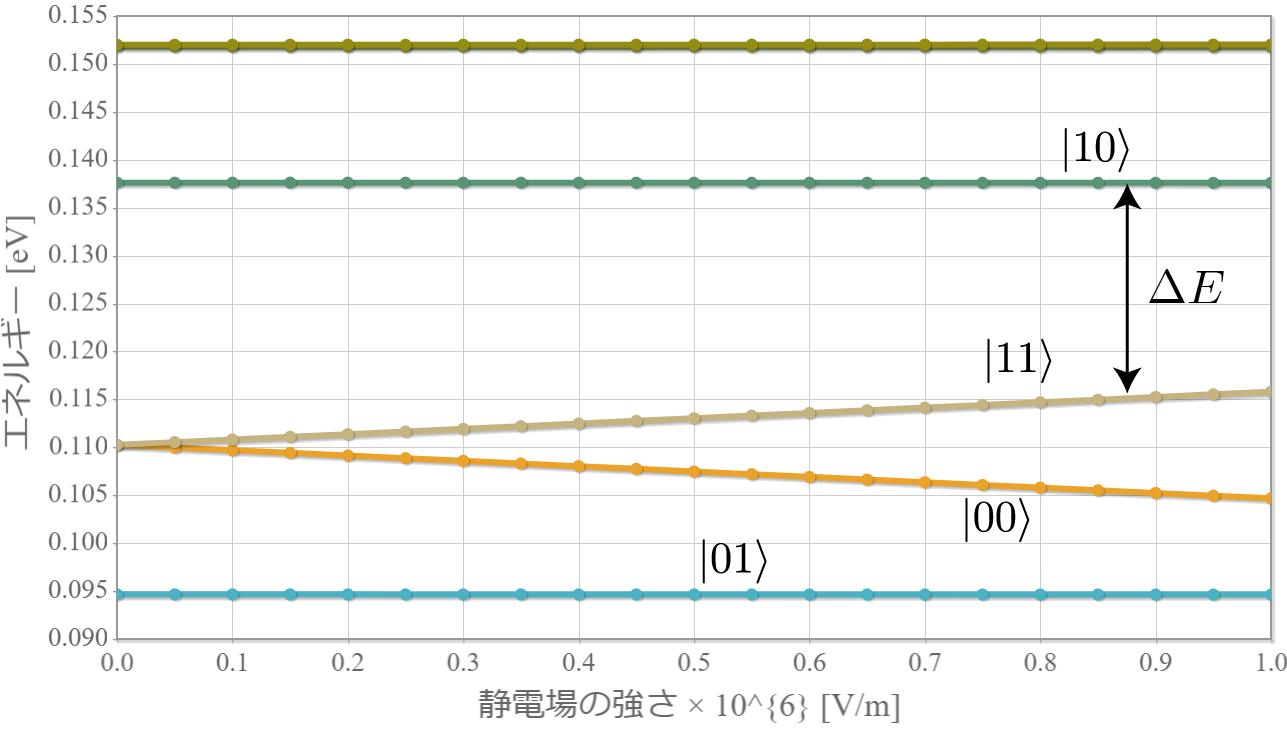
次の図は、上記の固有状態に対応するエネルギー準位の静電場の強度 $E_x$ 依存性だよ。想定通り、電場強度に比例して第１励起状態と第２励起状態の縮退が解けていく様子がわかるね。まさにシュタルク効果だね。今回は、エネルギー準位とは関係せずに電子が左か右かで $|0\rangle, |1\rangle$ を定義したけれども、エネルギー準位を基準として、２つの量子井戸の外側と内側で $|0\rangle, |1\rangle$ を定義すれば、固有エネルギーの低い順に $|00\rangle, |01\rangle, |10\rangle, |11\rangle$ と並ばせることもできるね。そして、下図の $\Delta E$ に対応する電磁波を外部から照射すれば、ラビ振動で $|10\rangle$ と $|11\rangle$ の状態遷移を起こすことができるので、制御・NOT演算が実現できるね。

次回は実際にラビ振動をシミュレーションして、制御・NOT演算を確かめてみよう！