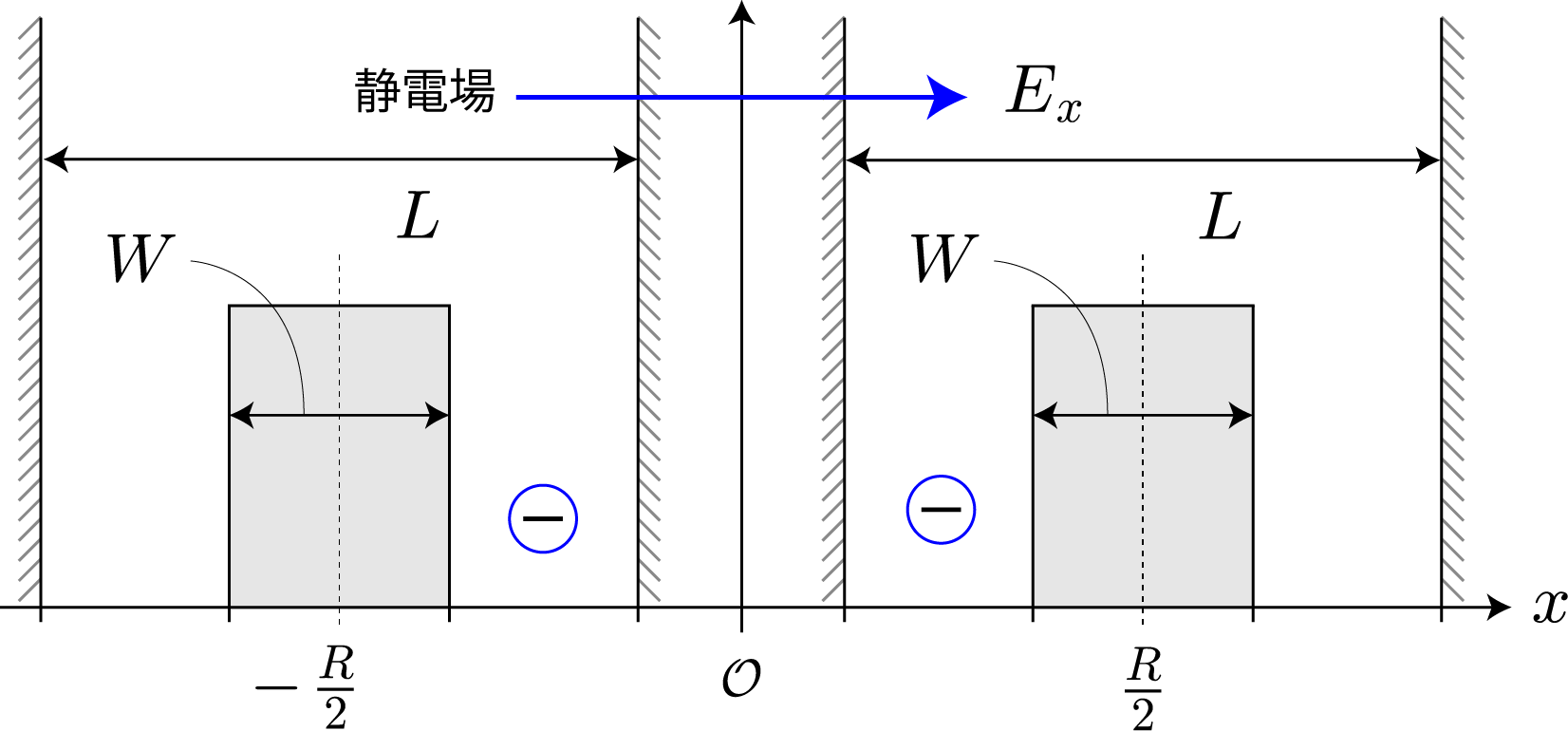
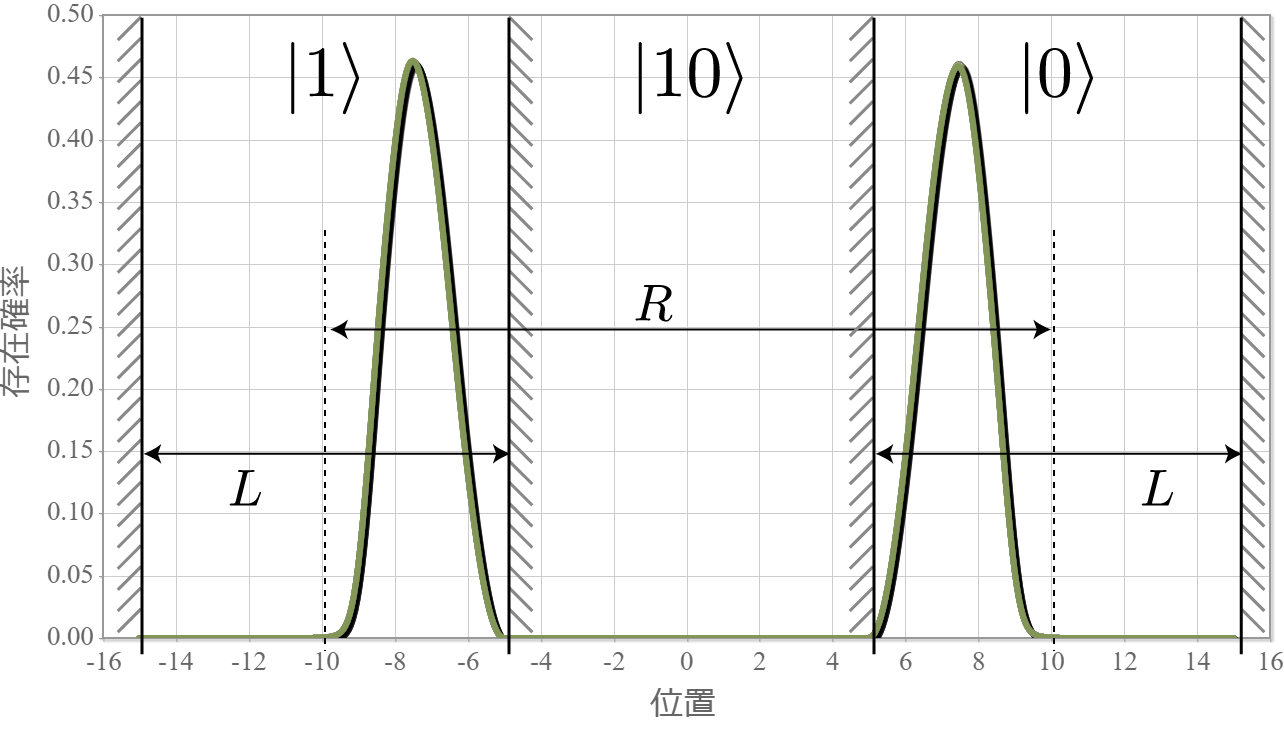
前回、電子同士のクーロン相互作用を考慮した独立した2つの2重量子井戸の電子の固有状態を計算したね。今回はさらに静電場を加えるね。壁の幅と高さは、$W = L/5= 2.0 \times 10^{-9} [{\rm m}] = 2.0[{\rm nm}]$、$V_0 = 3.0[{\rm eV}]$ として、量子井戸の間隔は $R = 20.0[{\rm nm}]$ とするよ。次の結果は、静電場の大きさを $E_x = 0.1\times10^{6}[{\rm V/m}]$ から $1.0\times10^{6}[{\rm V/m}]$ まで $ 0.05\times10^{6}[{\rm V/m}]$ づつ強くしたときの基底状態から第3励起状態までの電子存在確率の空間分布だよ。想定通りだけれども、ちょっとした静電場で第1励起状態と第2励起状態の縮退が解けて、2重量子井戸の壁の左右に分かれる形になったね。それぞれの量子井戸の左に電子がいる状態を $|0\rangle$、右にいる状態を$|1\rangle$ と表すと、それぞれの電子状態は固有エネルギーが低い順番に $|01\rangle, |00\rangle, |10\rangle, |11\rangle$ と表わすことができるね。
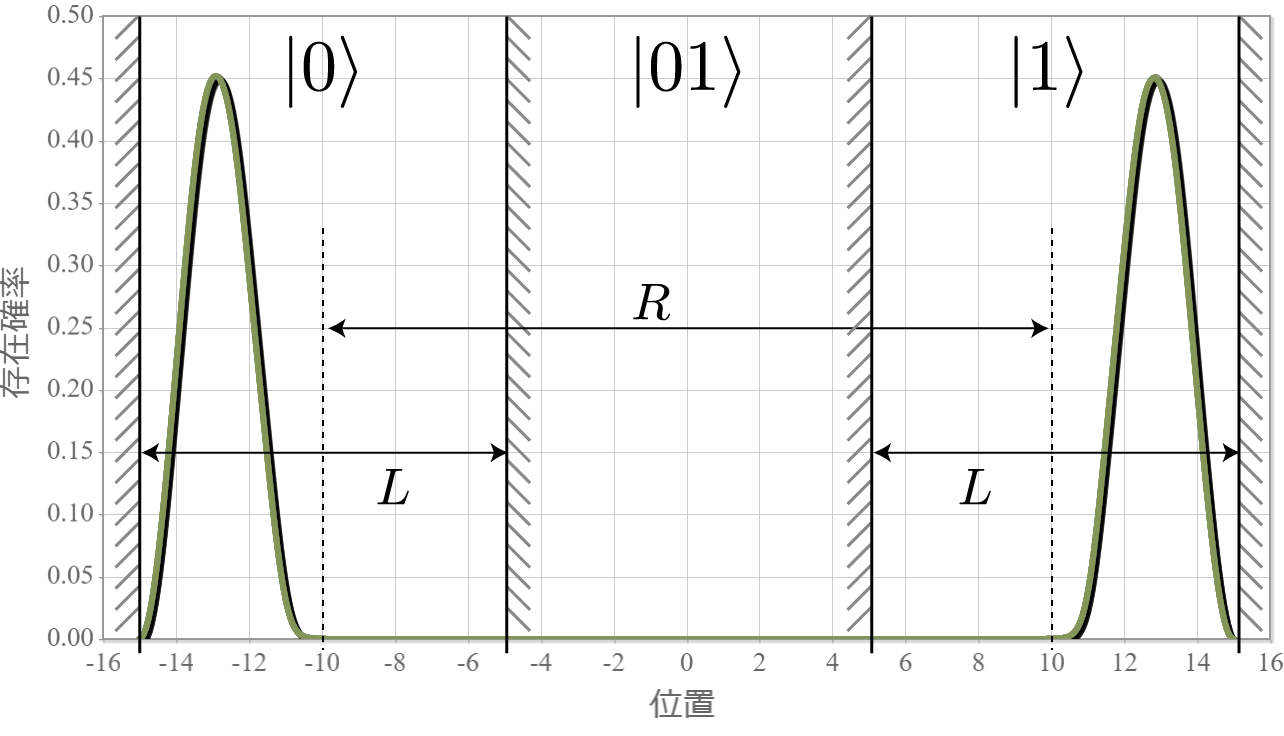
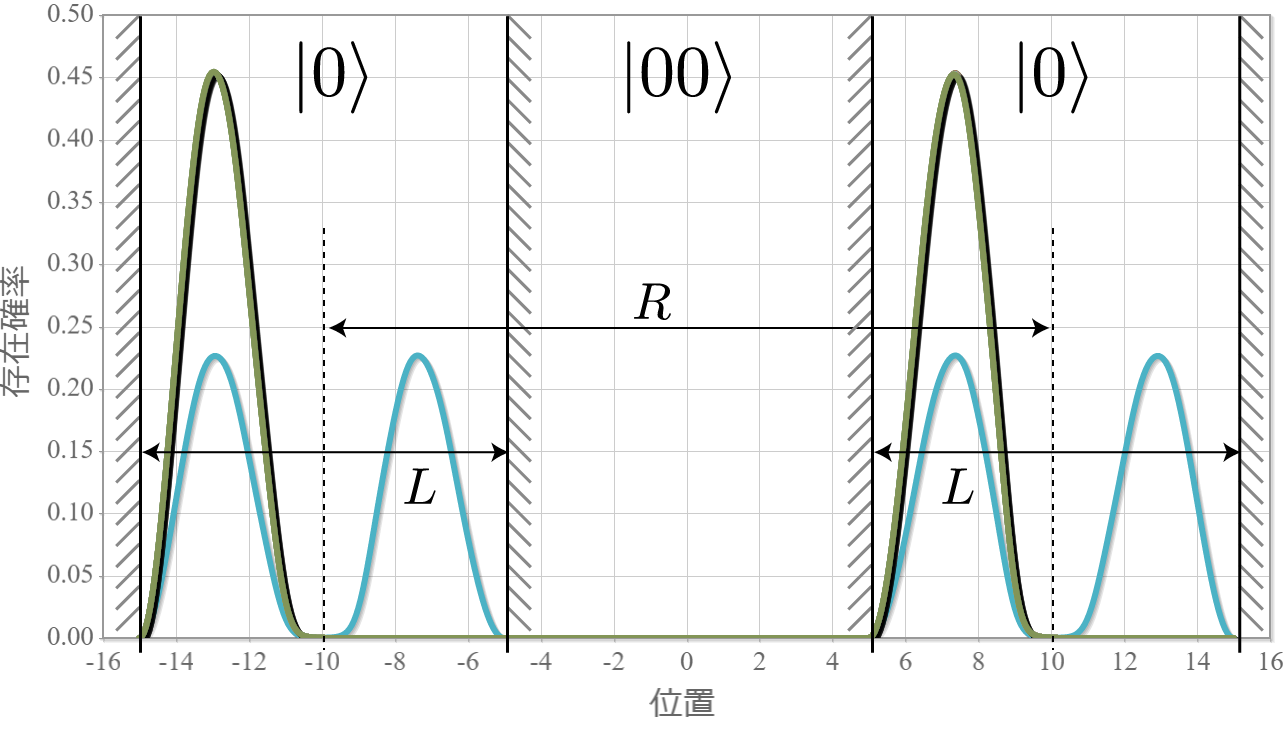
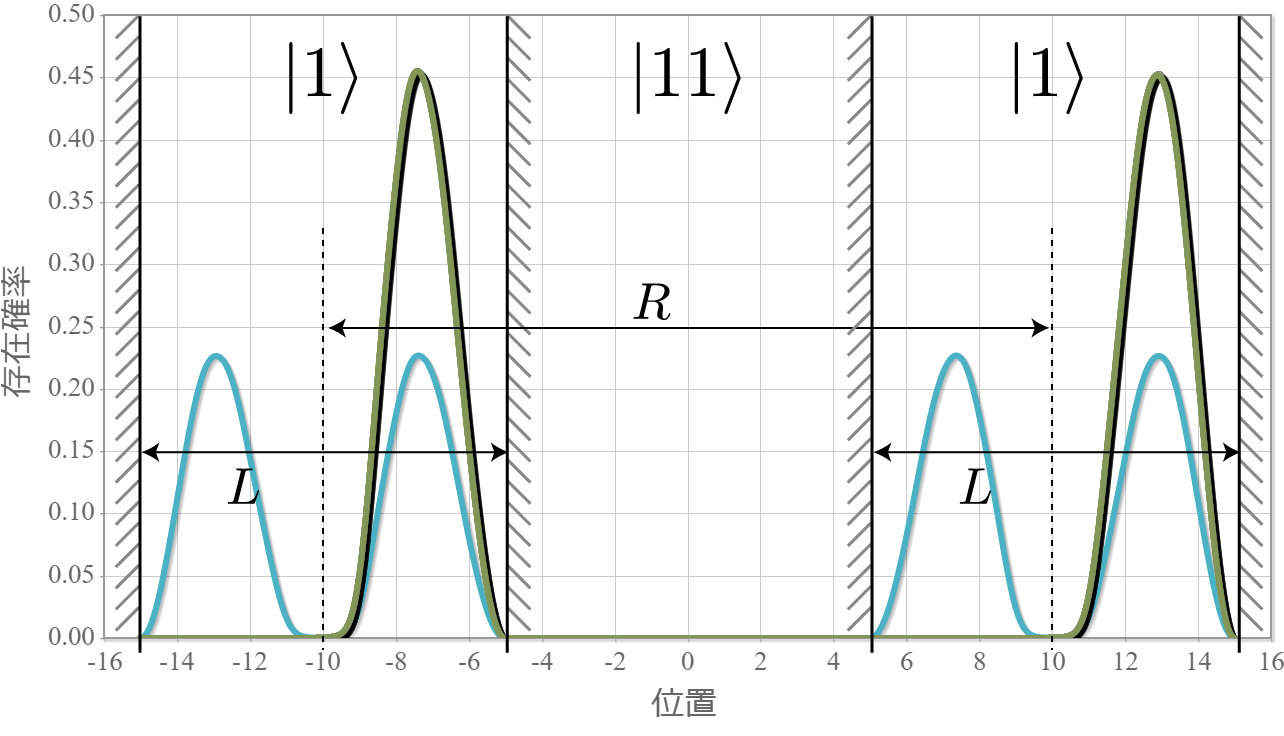
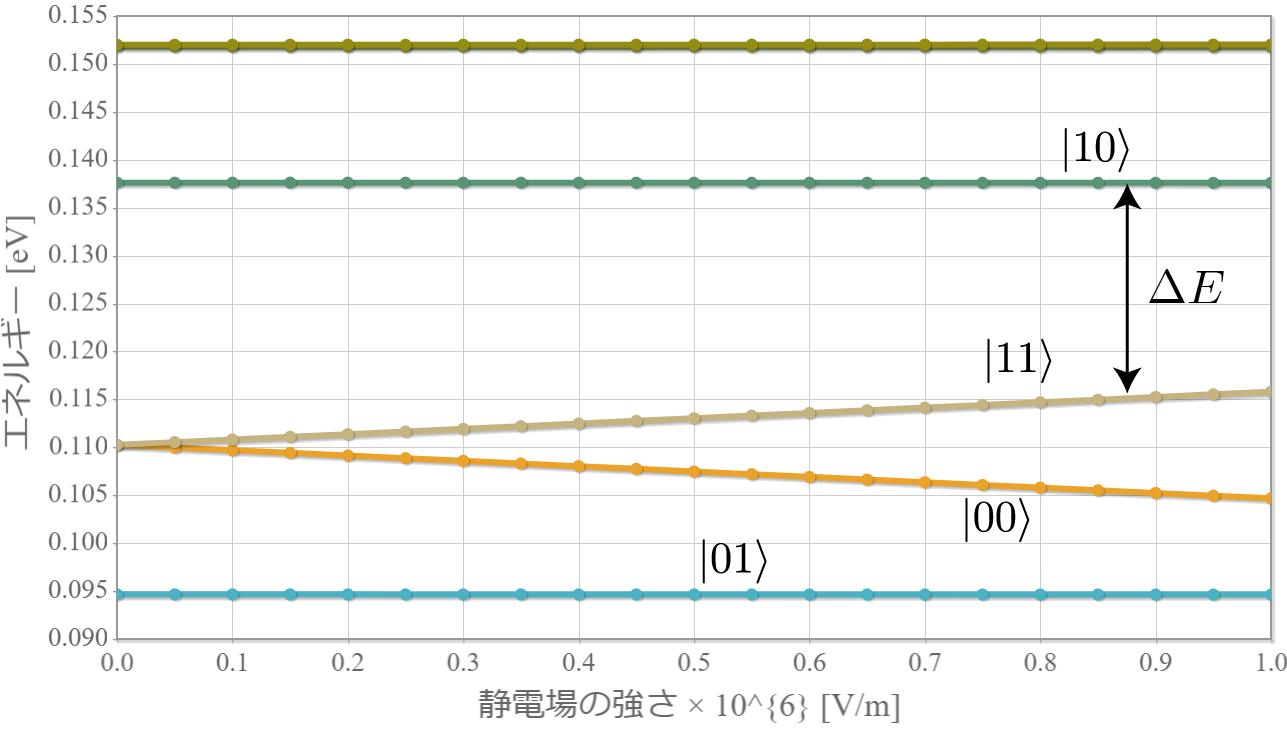
次の図は、上記の固有状態に対応するエネルギー準位の静電場の強度 $E_x$ 依存性だよ。想定通り、電場強度に比例して第1励起状態と第2励起状態の縮退が解けていく様子がわかるね。まさにシュタルク効果だね。今回は、エネルギー準位とは関係せずに電子が左か右かで $|0\rangle, |1\rangle$ を定義したけれども、エネルギー準位を基準として、2つの量子井戸の外側と内側で $|0\rangle, |1\rangle$ を定義すれば、固有エネルギーの低い順に $|00\rangle, |01\rangle, |10\rangle, |11\rangle$ と並ばせることもできるね。そして、下図の $\Delta E$ に対応する電磁波を外部から照射すれば、ラビ振動で $|10\rangle$ と $|11\rangle$ の状態遷移を起こすことができるので、制御・NOT演算が実現できるね。
次回は実際にラビ振動をシミュレーションして、制御・NOT演算を確かめてみよう!

“【量子コンピュータを作ろう!】(15)2つの独立した量子井戸に束縛された電子の基礎実験3:クーロン相互作用+静電場(2重量子井戸)” への2件の返信