【量子コンピュータを作ろう！】（14）２つの独立した量子井戸に束縛された電子の基礎実験２：クーロン相互作用（２重量子井戸）

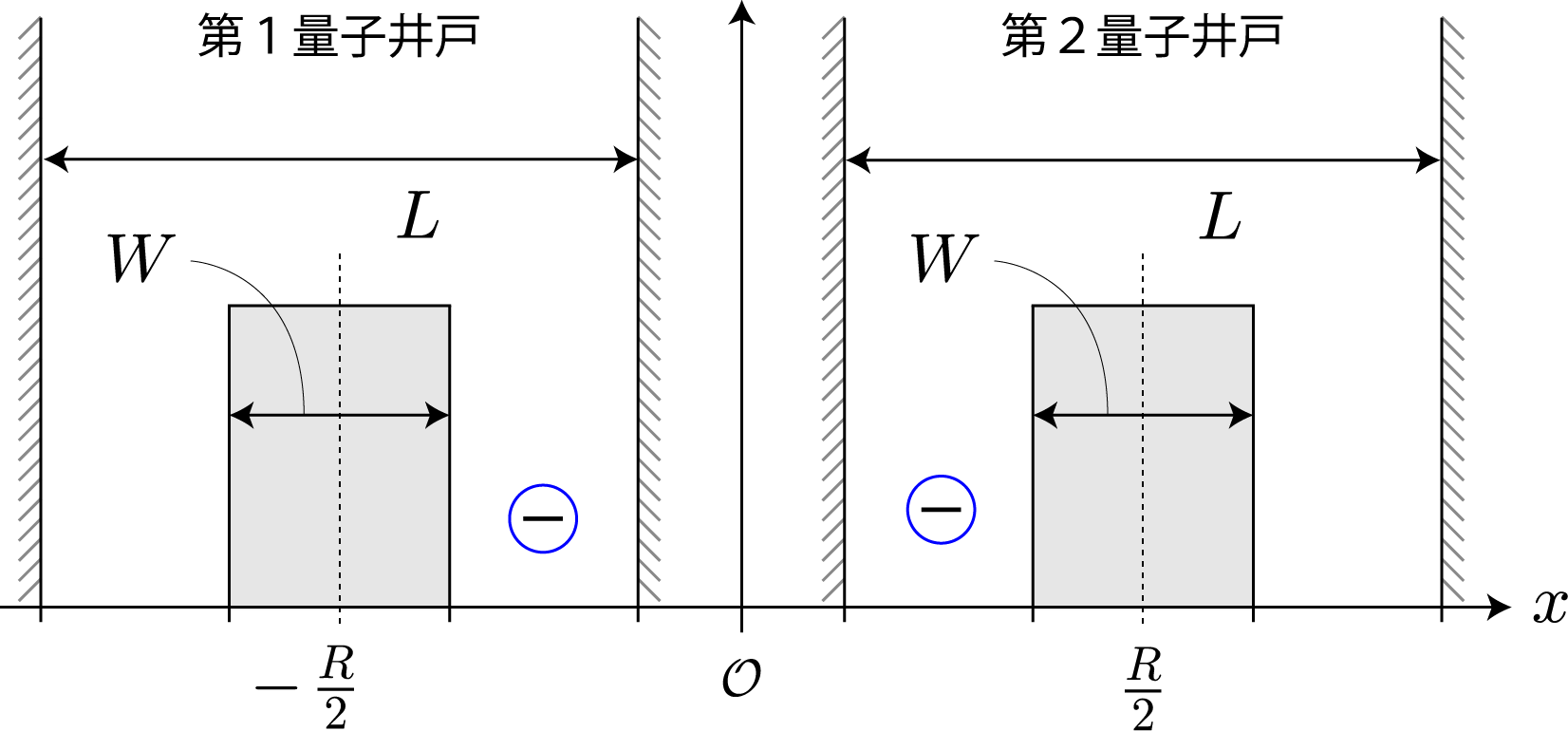
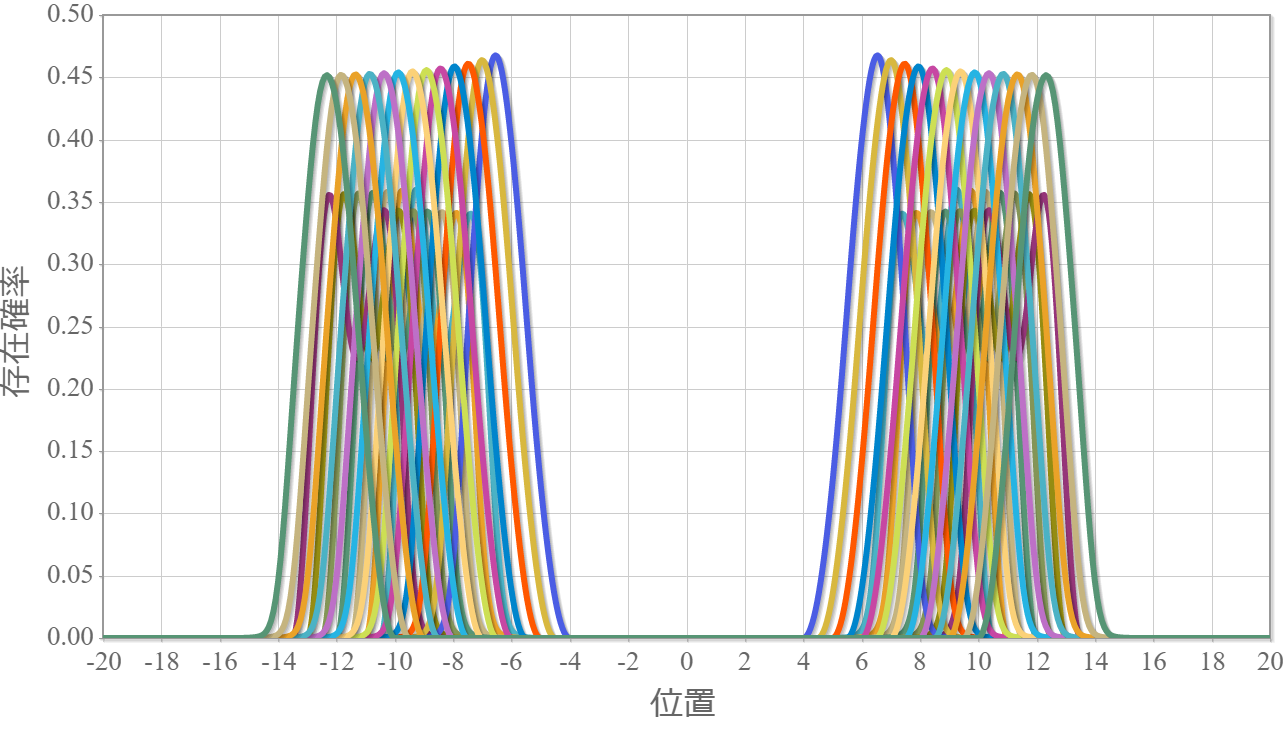
前回、２つの独立した量子井戸の電子同士のクーロン相互作用を考慮した固有状態を計算したね。今回は、静電場を加える前に、量子井戸を右図のような２重量子井戸にした場合の固有状態を計算しておくね。壁の幅と高さは第９回の結果を踏まえて、$W = L/5= 2.0 \times 10^{-9} [{\rm m}] = 2.0[{\rm nm}]$、$V_0 = 3.0[{\rm eV}]$ とするよ。次の結果は、２つの量子井戸の間隔を $R = 11[{\rm nm}]$ から $ 30 [{\rm nm}]$ まで $ 1 [{\rm nm}]$ づつ広げていったときの基底状態から第３励起状態までの電子存在確率の空間分布だよ。間に壁を作ったことで、クーロン相互作用の反発があるにも関わらず、波形が綺麗になったね。

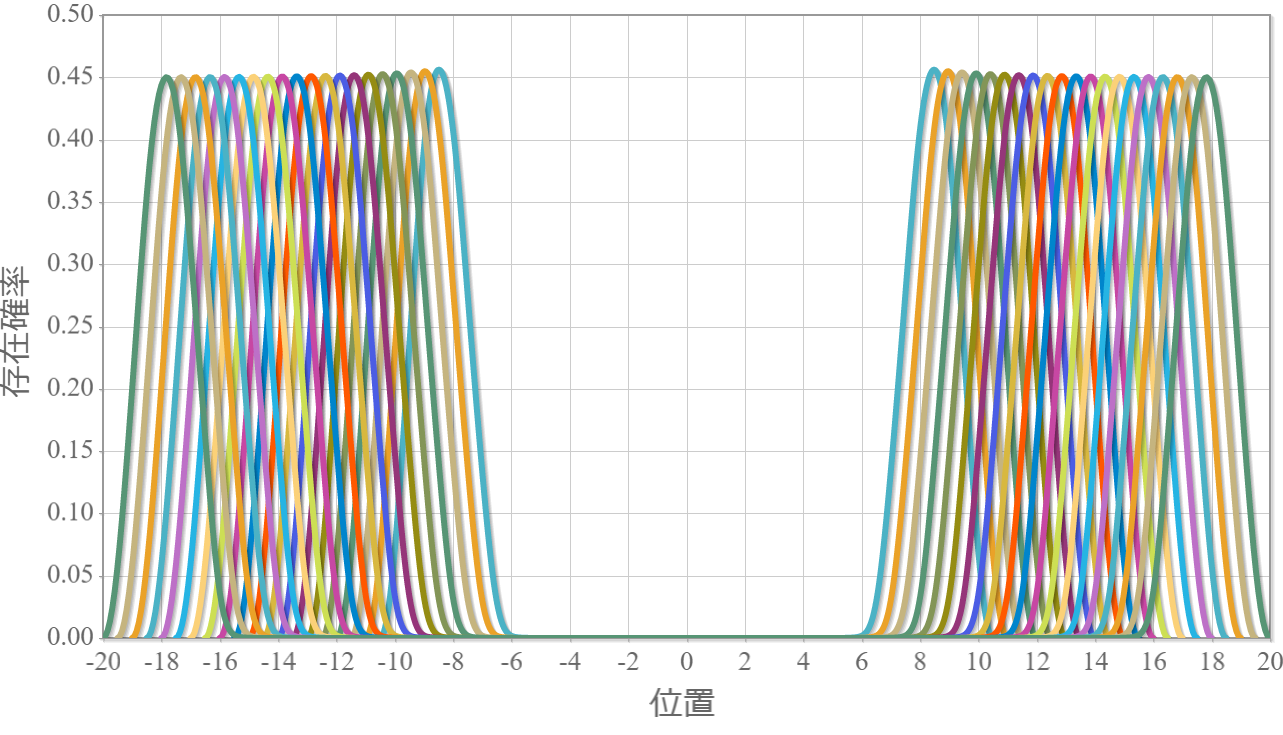
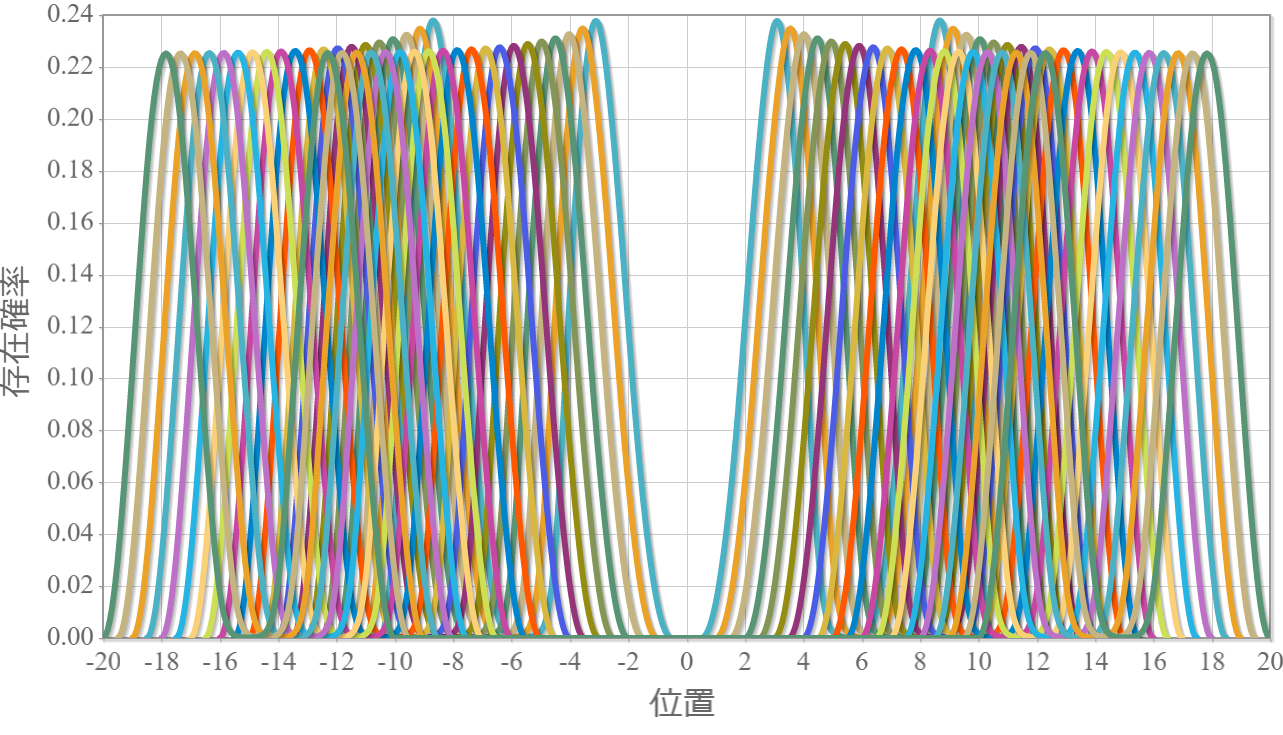
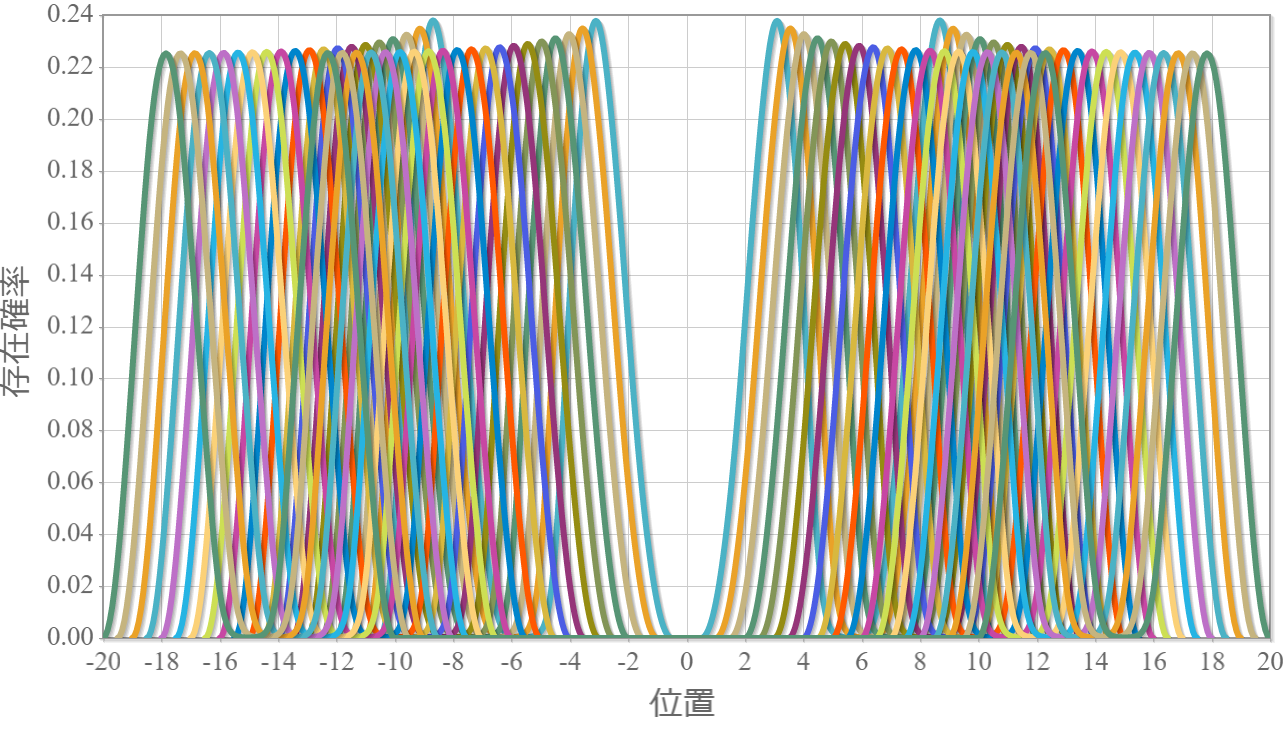
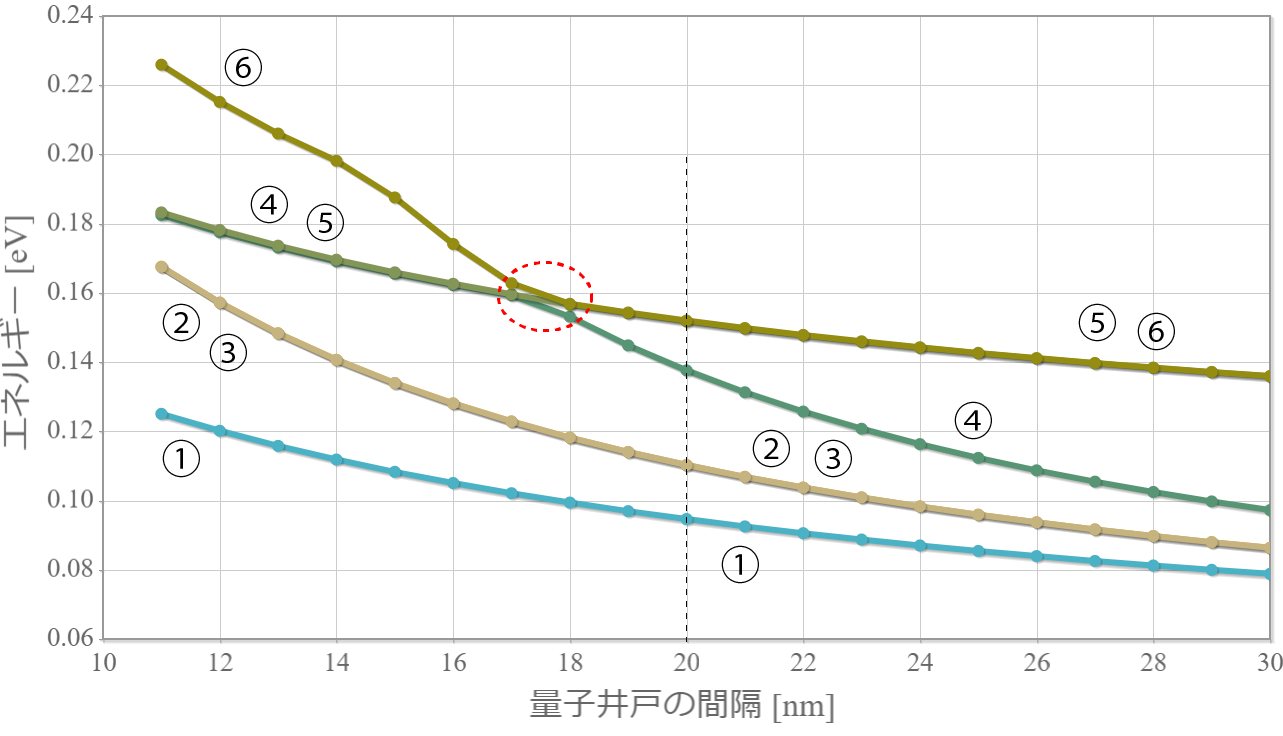
次の図は、上記の固有状態に対応するエネルギー準位の量子井戸間の距離 $R$ 依存性だよ。図中の①～⑥はそれぞれの $R$ に対してエネルギーが低い順（基底状態、第１励起状態、・・・、第５励起状態）だけれども、興味深いのは、$R \sim 1.8 [{\rm nm}]$ 近傍でエネルギー準位が交差しているね。この距離よりも大きい場合に、クーロン相互作用を考慮しない場合と同様の状況（基底状態：縮退なし、第１励起状態と第２励起状態が縮退、第３励起状態：縮退なし）を作れるね。つまり、２つの量子井戸の間隔がある程度離れていないと、クーロン相互作用が強すぎることを意味しているね。

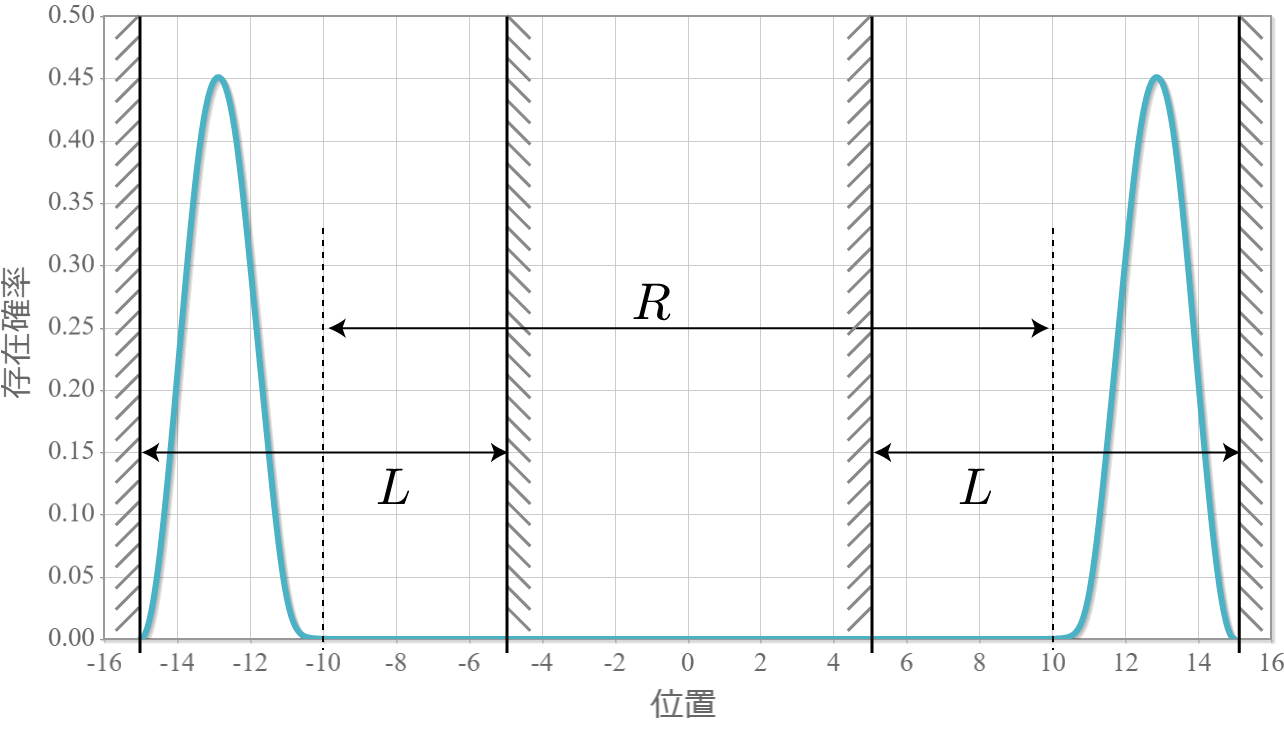
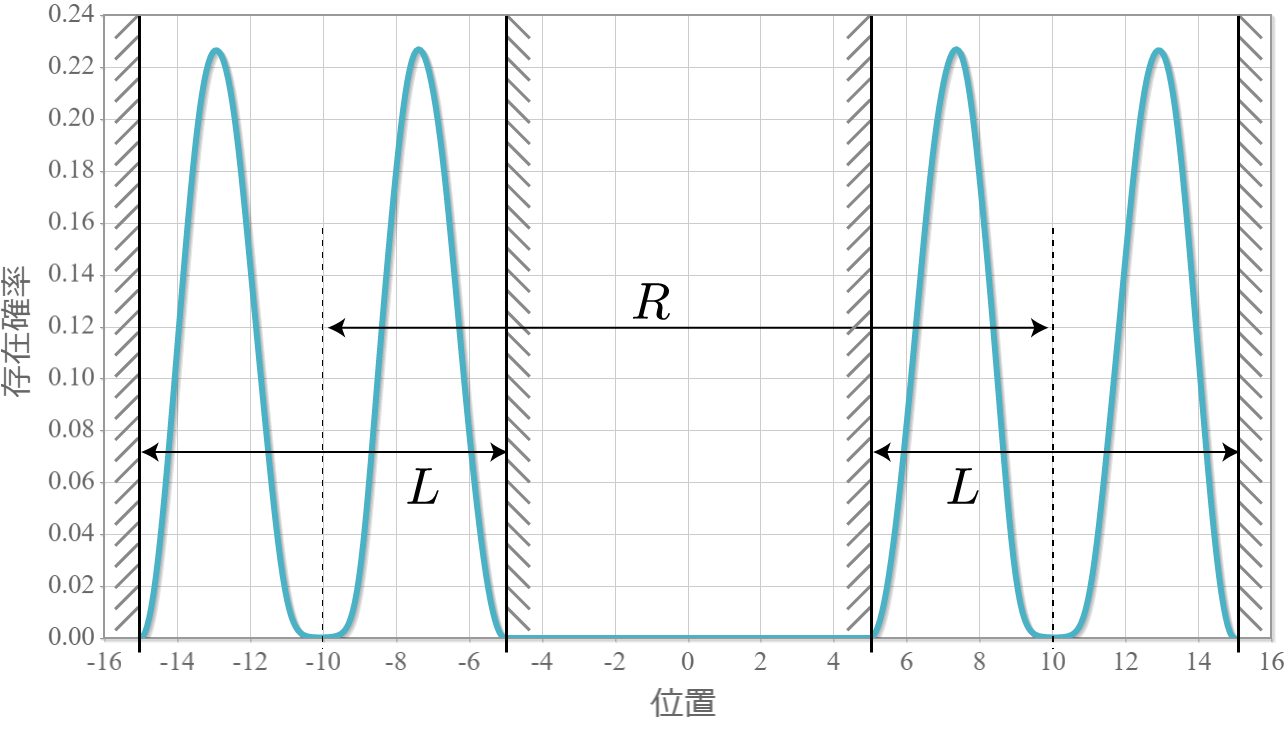
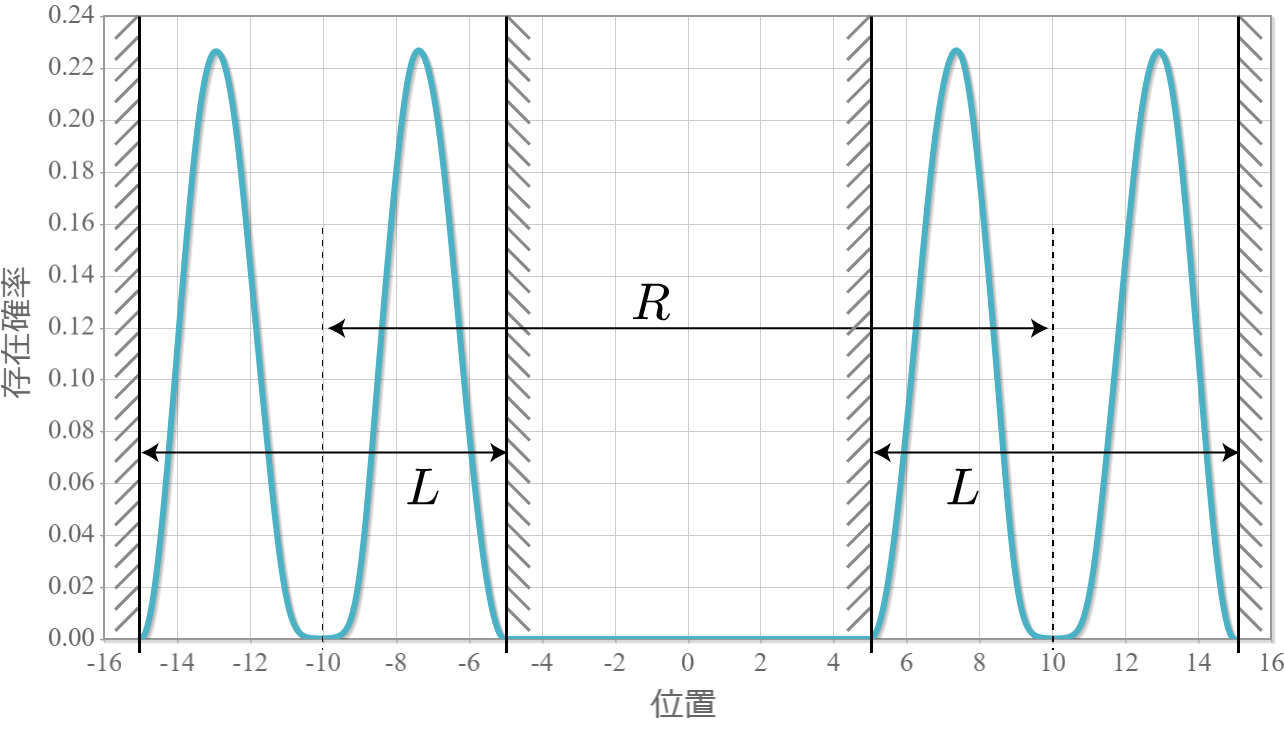
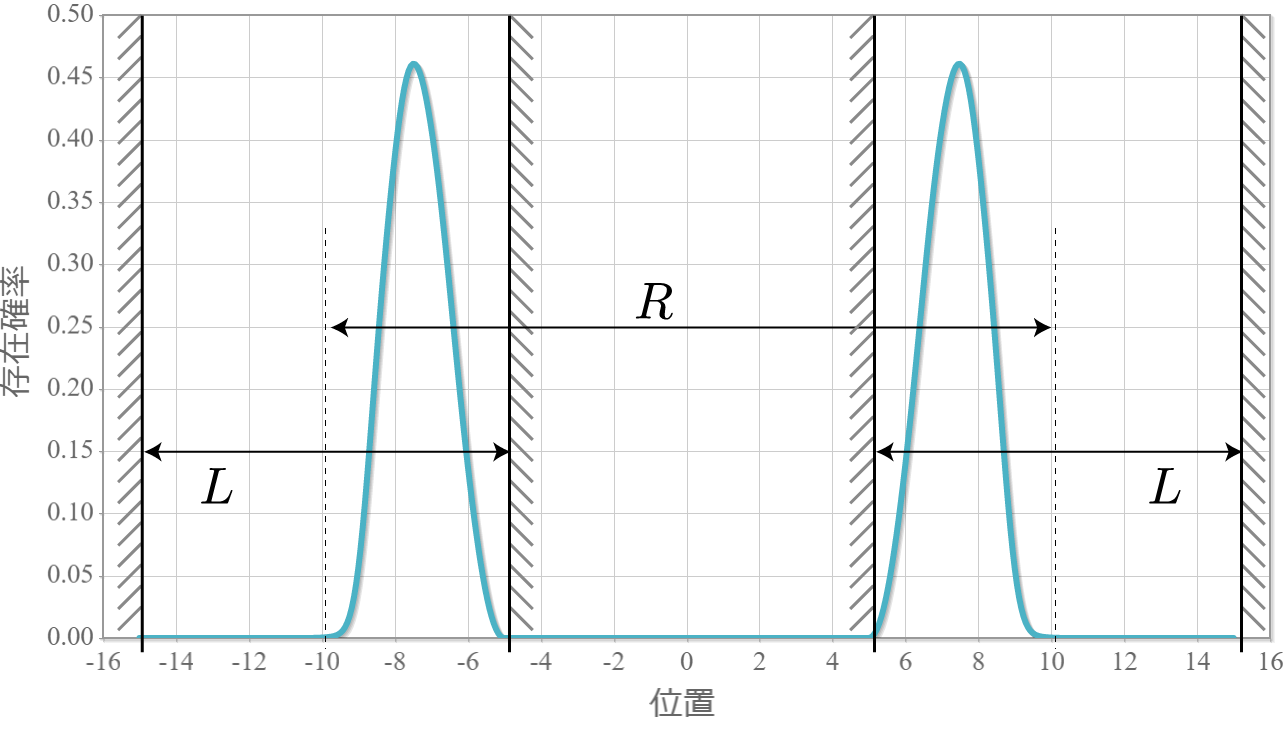
先の固有状態のうち、$R = 2.0 [{\rm nm}]$ だけの、基底状態から第三励起状態までを並べたのが次の結果だよ。先にも言ったけれども、クーロン相互作用があるようには思えないほど波形が綺麗だね。基底状態と第３励起状態で電気双極子モーメントが反対向き、第１励起状態と第２励起状態で電気双極子モーメントは０になっているね。

次回はこの状態に静電場を加えてみるね。