水素原子に電場を加えたときの波動関数を可視化してみよう！（１次のシュタルク効果の正体が判明！）

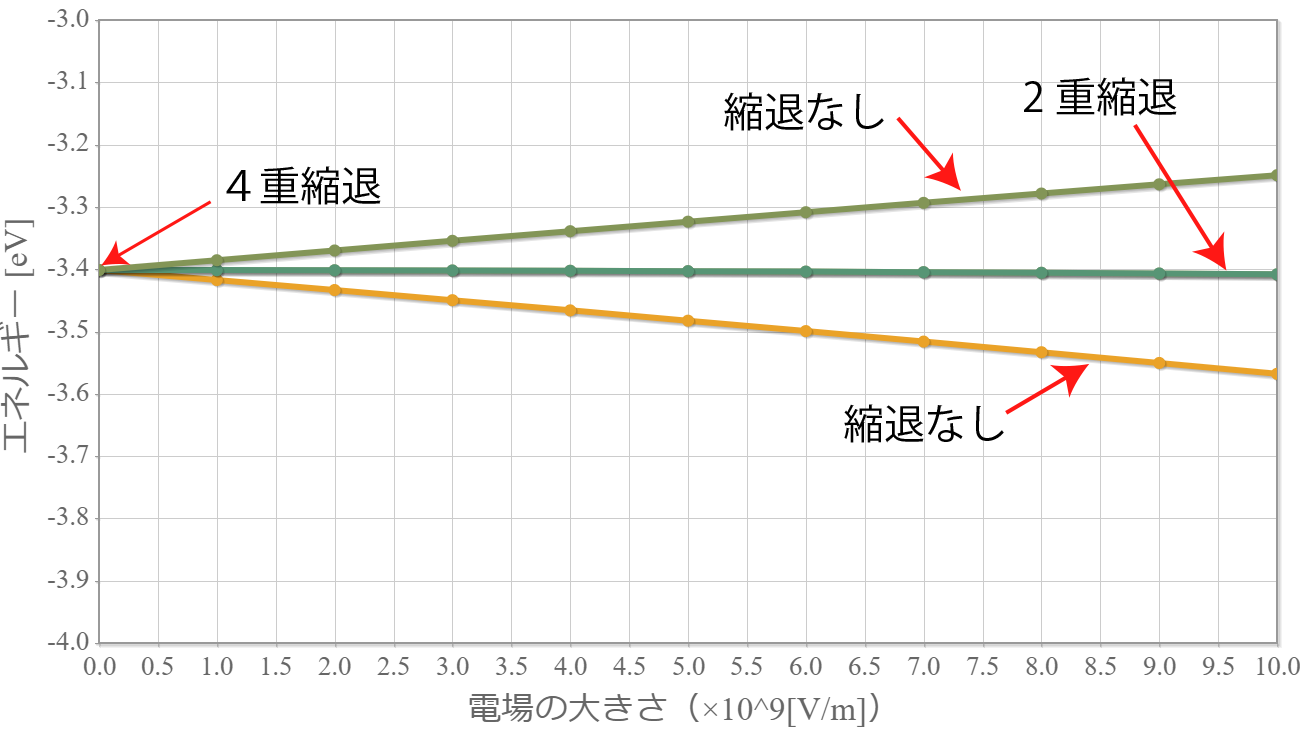
前回、水素原子に電場を加えたときのエネルギー準位の変化をシミュレーションしたね。
具体的には４重縮退だった第一励起状態（2s軌道と2p軌道）は、電場を加えることで２つの縮退がない状態と１つの２重縮退の状態に別れたね。
この状態に着目して電場を加えたときの電子の波動関数の様子をシミュレーションしてみよう！

電場がない場合の第１励起状態の固有状態を復習しよう！

電場がない状態で４重縮退している第一励起状態2s軌道（$n=2, l=0, m=0$）と2p軌道（$n=2, l=1, m=\pm 1 , 0$）を復習しよう！
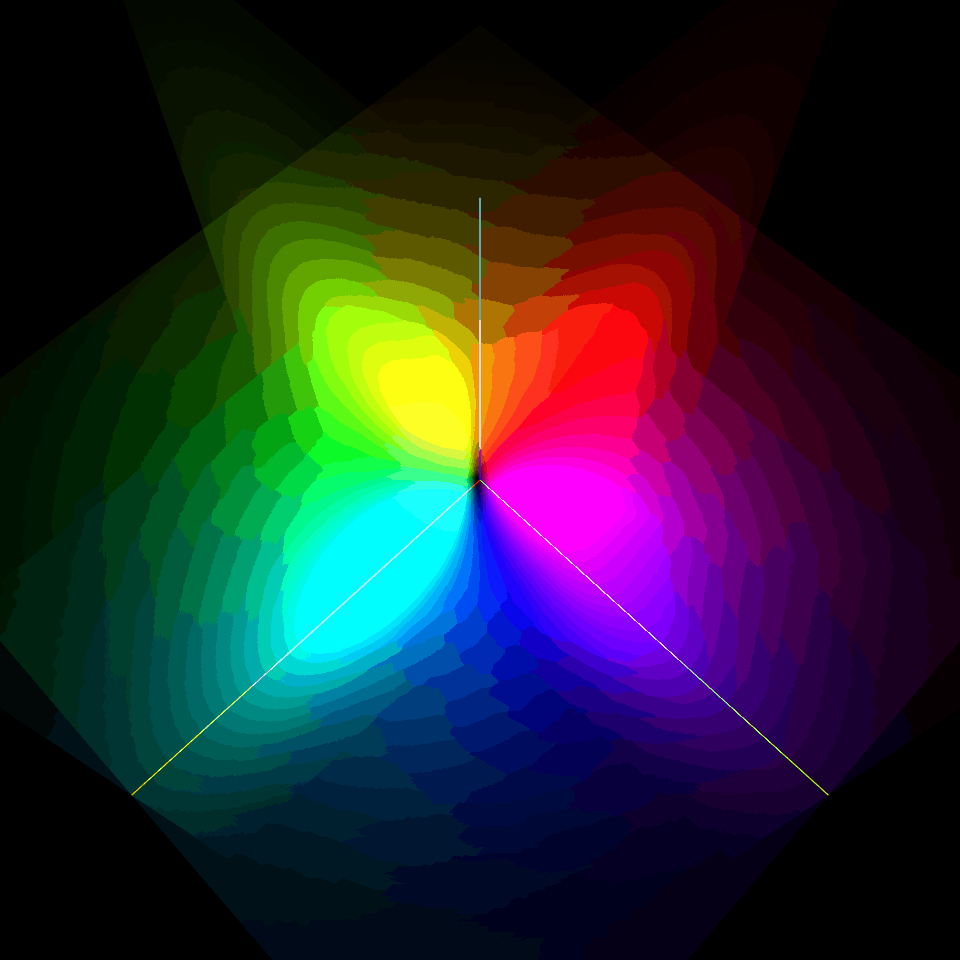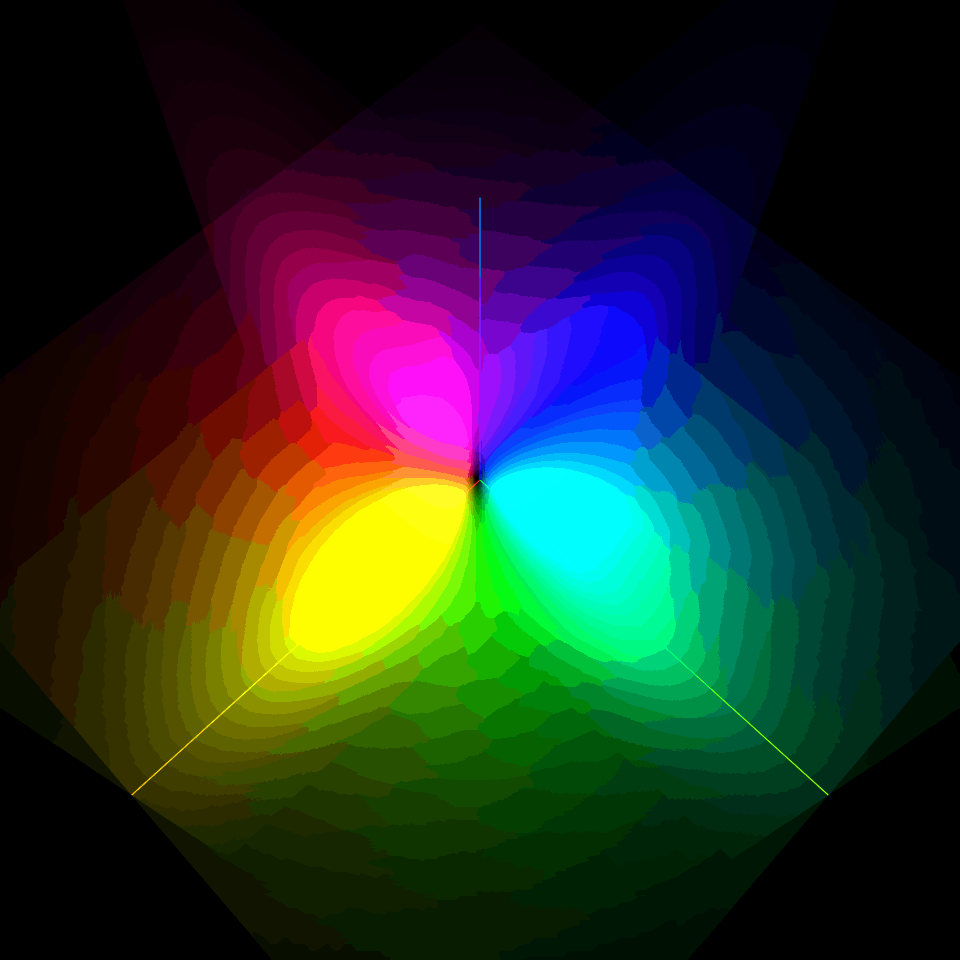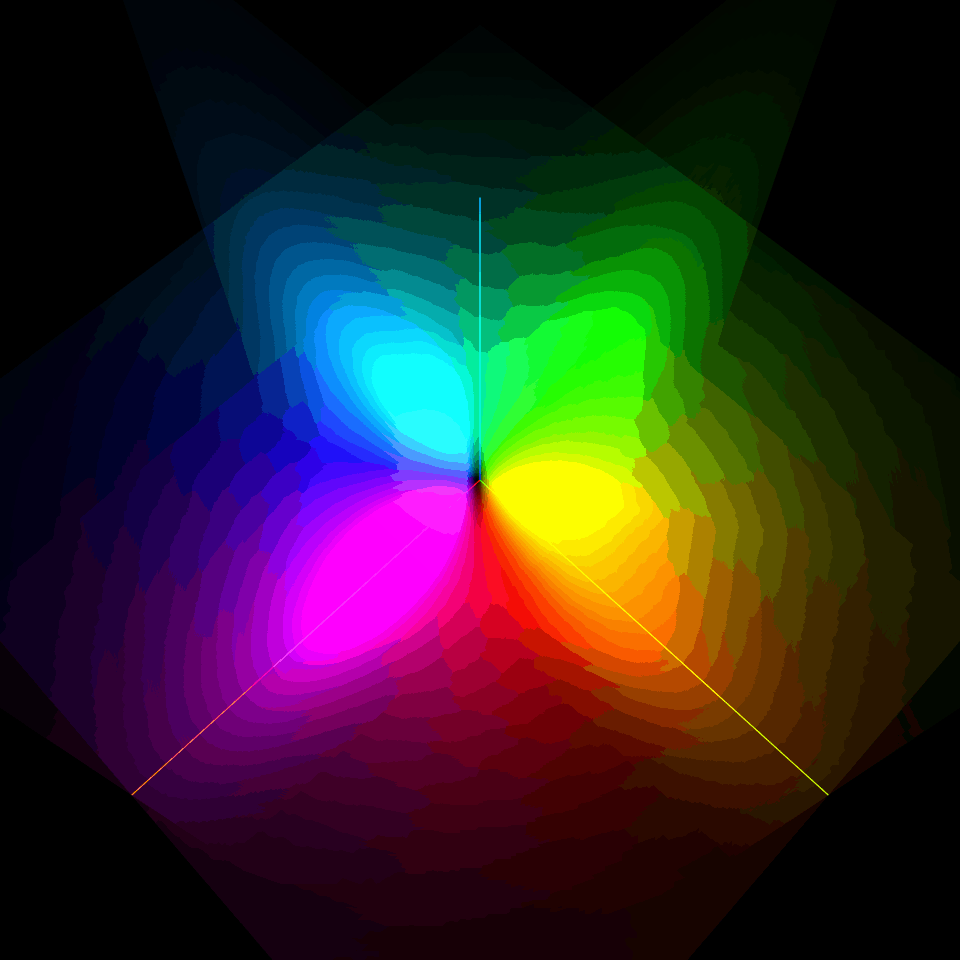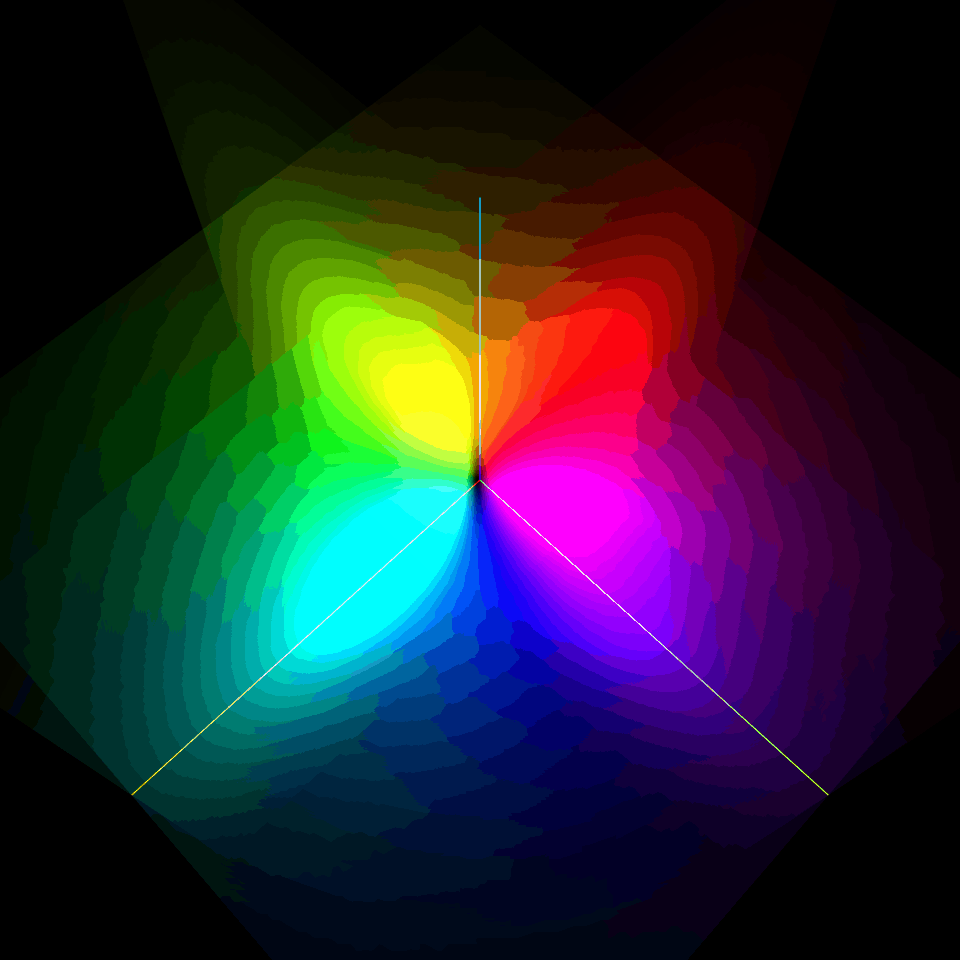
$l=0$の2s軌道は２重殻構造の球対称型、$l=1$の2p軌道は$m=0$がz軸に対する軸対称の８の字型、$m=-1$と$m=1$がz軸を中心にそれぞれ逆回転するドーナッツ型だったね。
これら４つの状態はエネルギーが同一であるため、電子はこれらの状態を自由に行き来することができるんよね。
つまり、このエネルギーに存在する電子の実際の波動関数はこれら４つの状態は自由な重ね合わせで表されることを理解しておこう！

$\varphi_{200}$	$\varphi_{21-1}$	$\varphi_{210}$	$\varphi_{21+1}$

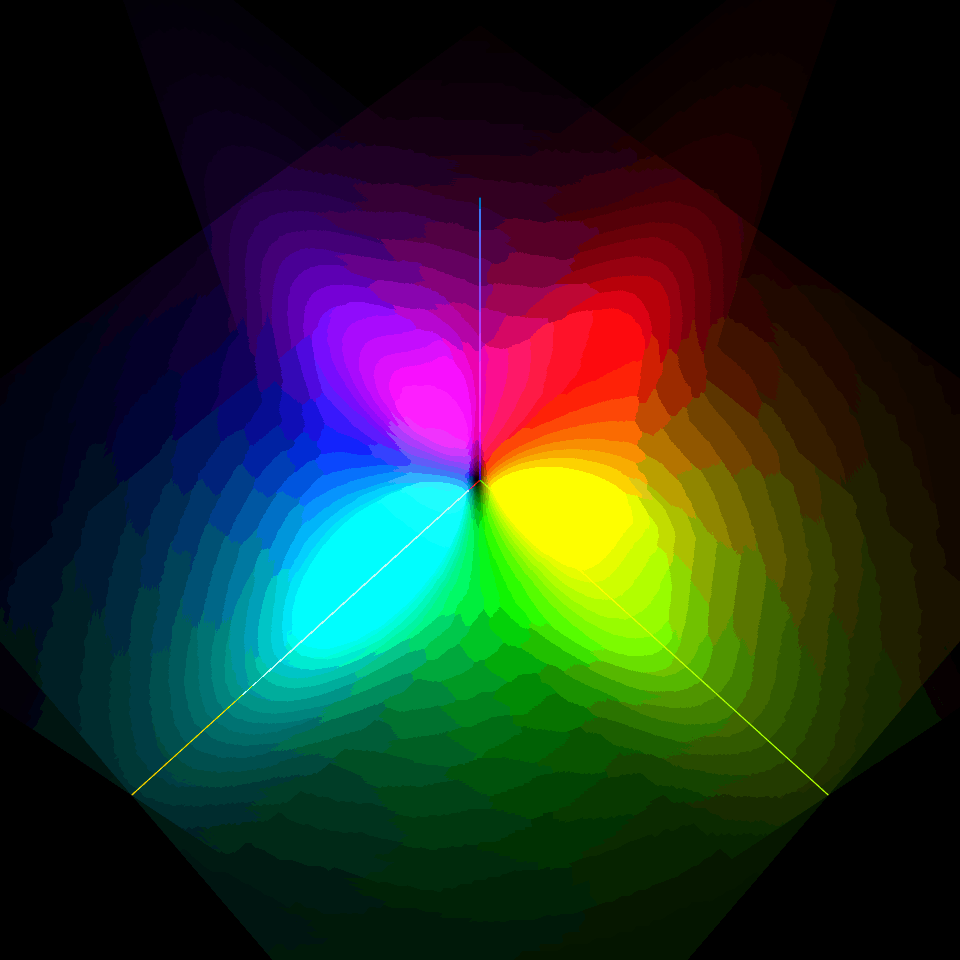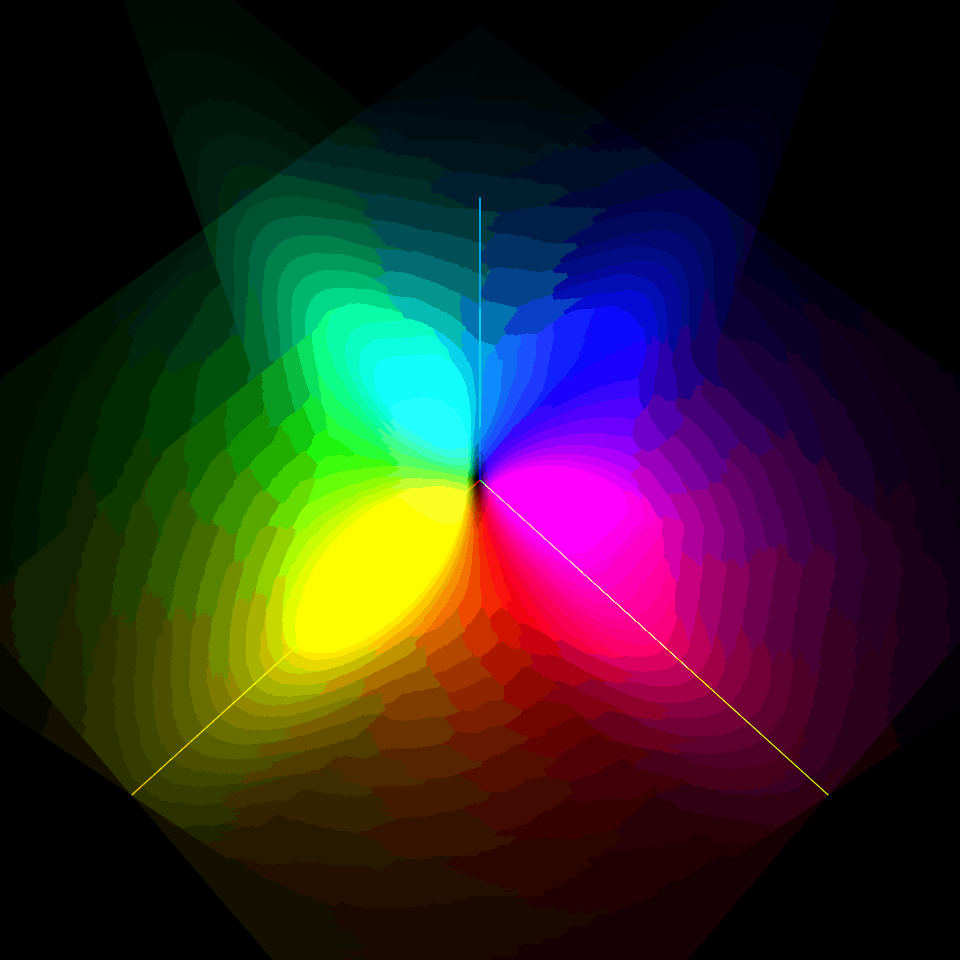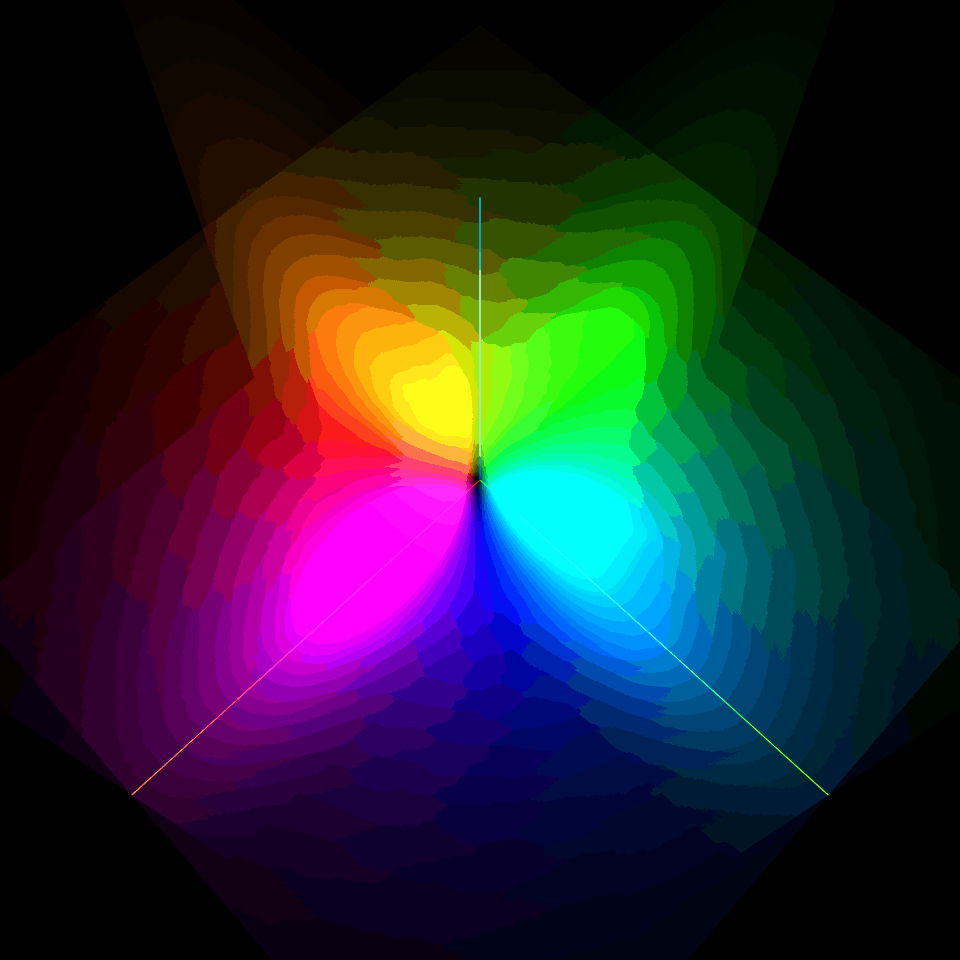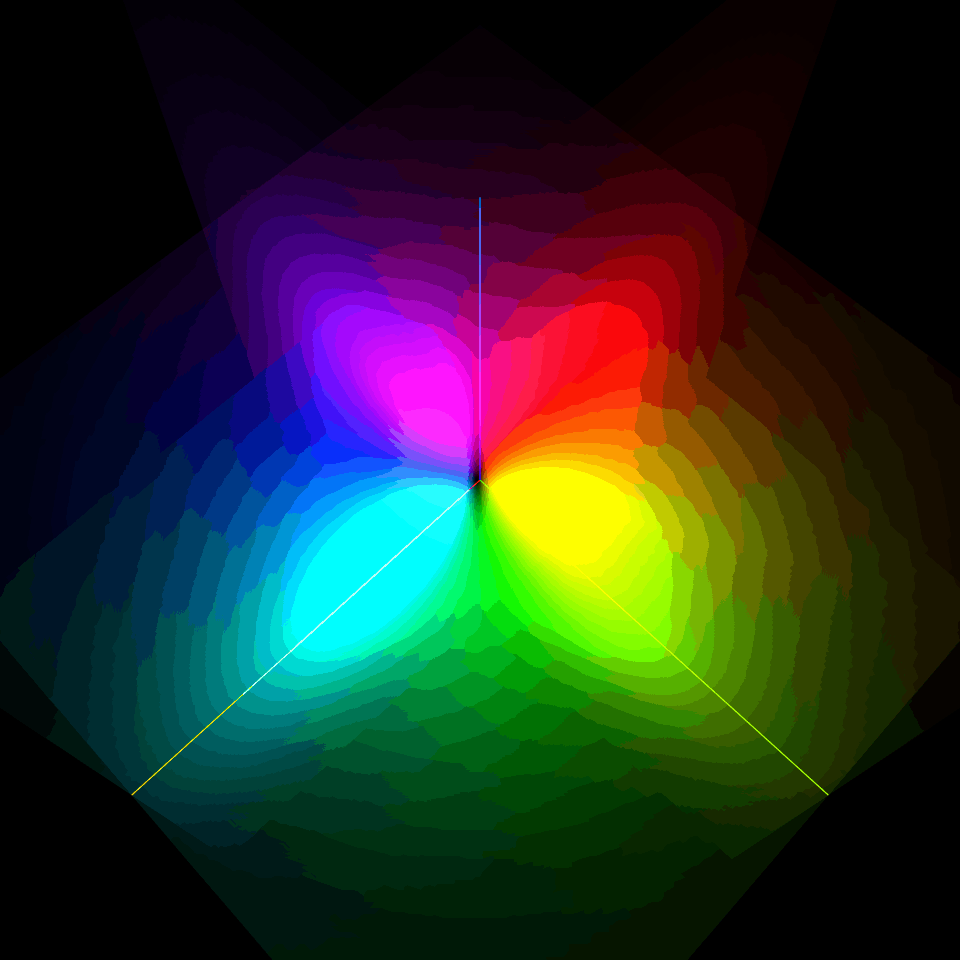エネルギーが最も低い固有状態をシミュレーション！

z軸方向に電場を加えるとどうなるだろう？さっそくシミュレーションしてみよう！次の図は、第１励起状態（n=2）で最もエネルギーが低い固有状態の成分の電場強度依存性を表した図だよ。

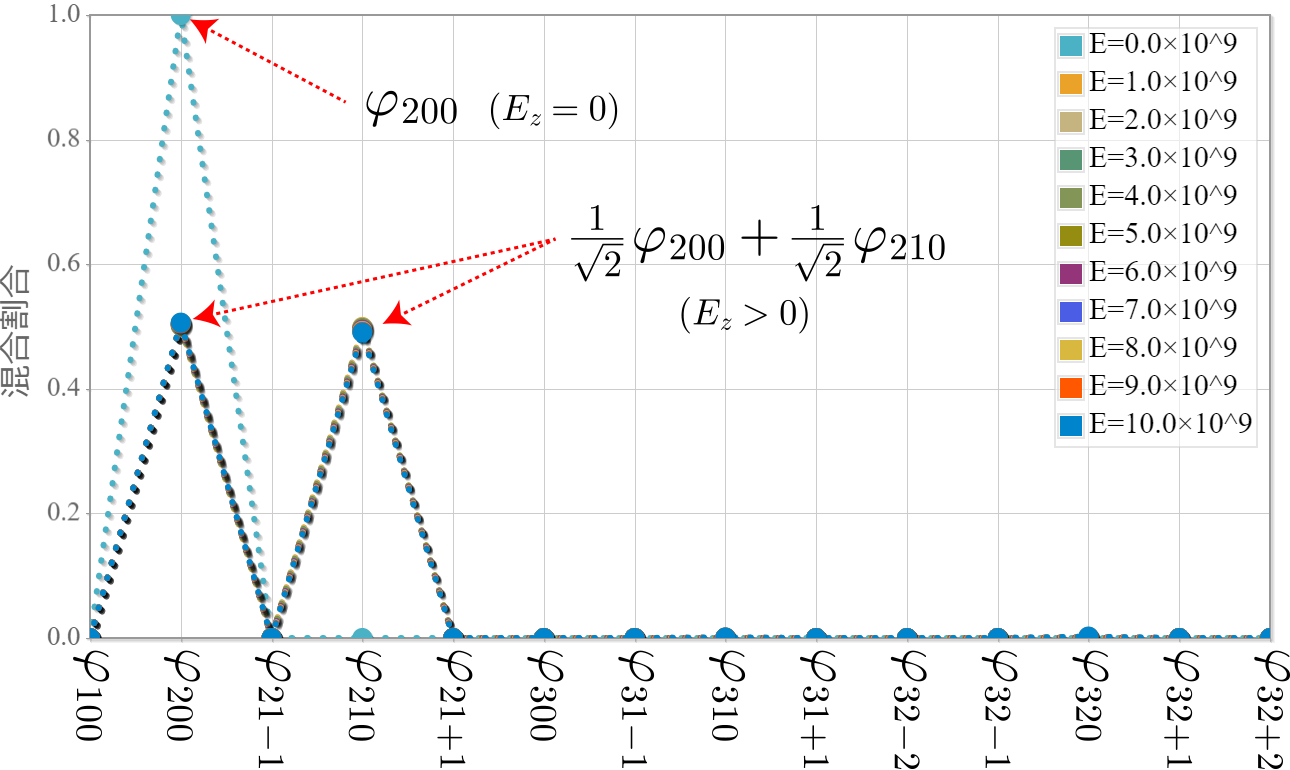
$E_z=0$のときに$\varphi_{200}$100%だった状態から、電場を加えた瞬間に$\varphi_{200}$と$\varphi_{210}$が50%づつ混ざった状態に変化したことを表しているよ。
この固有状態の波動関数を見てみよう！

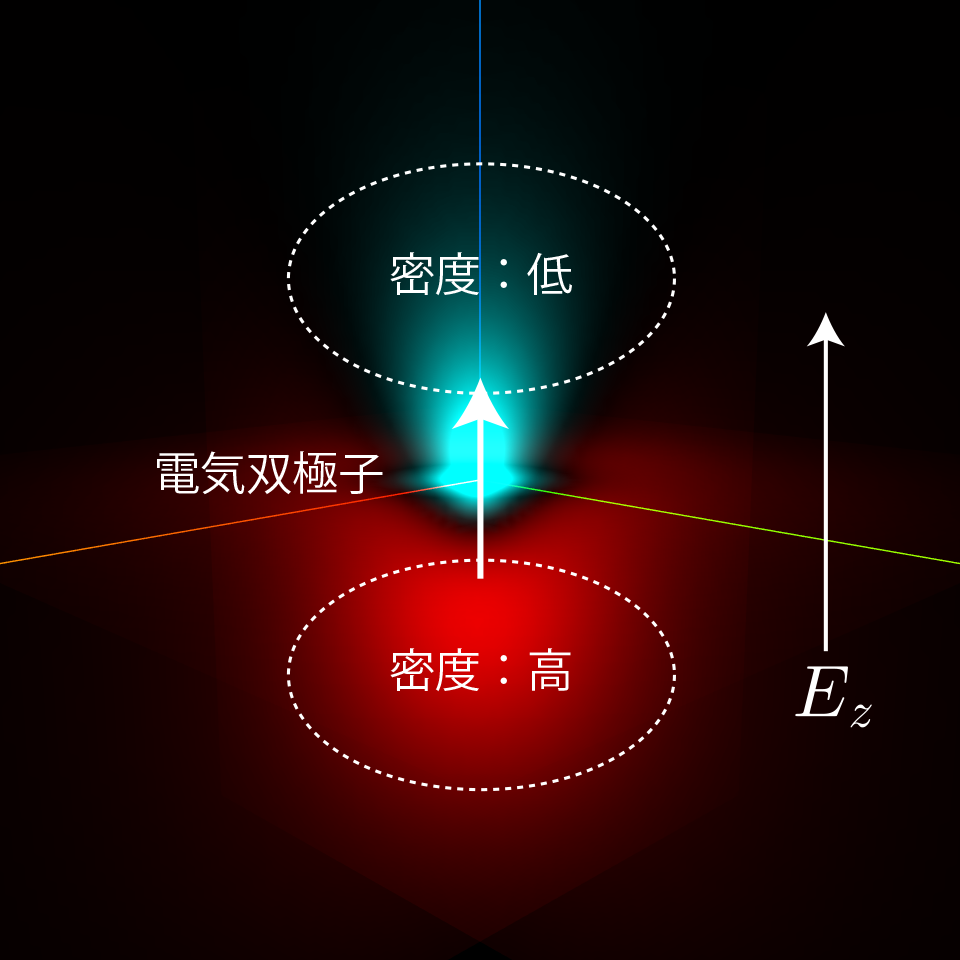
左図が単振動アニメーション、右図が静止画に説明を加えた図だよ。
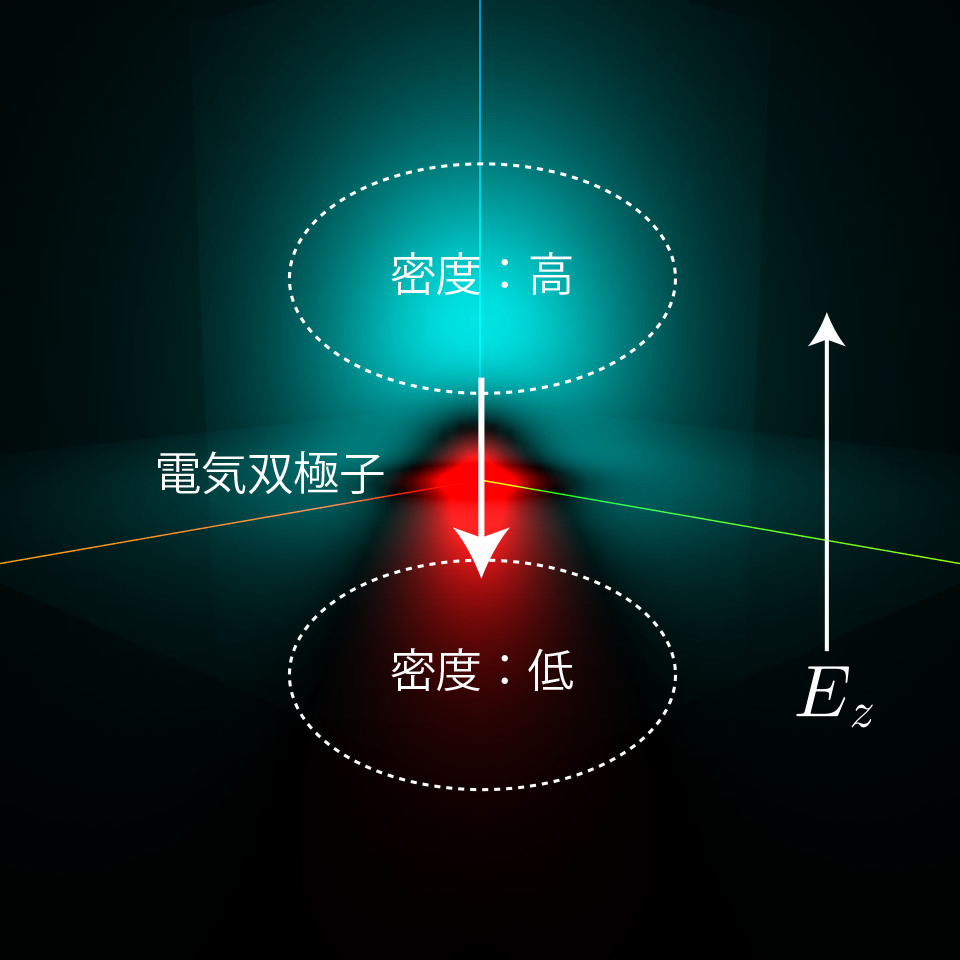
もともと$\varphi_{200}$と$\varphi_{210}$を重ねた状態は電子の分布がz軸方向で対称ではないから、電気双極子になっているんだね。
外部から電場が加えられるとエネルギーが低くくなる方向に電気双極子が向くんだね。

エネルギーが最も高い固有状態をシミュレーション！

第１励起状態（n=2）で最もエネルギーが低い固有状態の成分の電場強度依存性を表した図だよ。
同じ50%同士の重ね合わせでも符号が反対の場合には、エネルギーが高くなるよ。

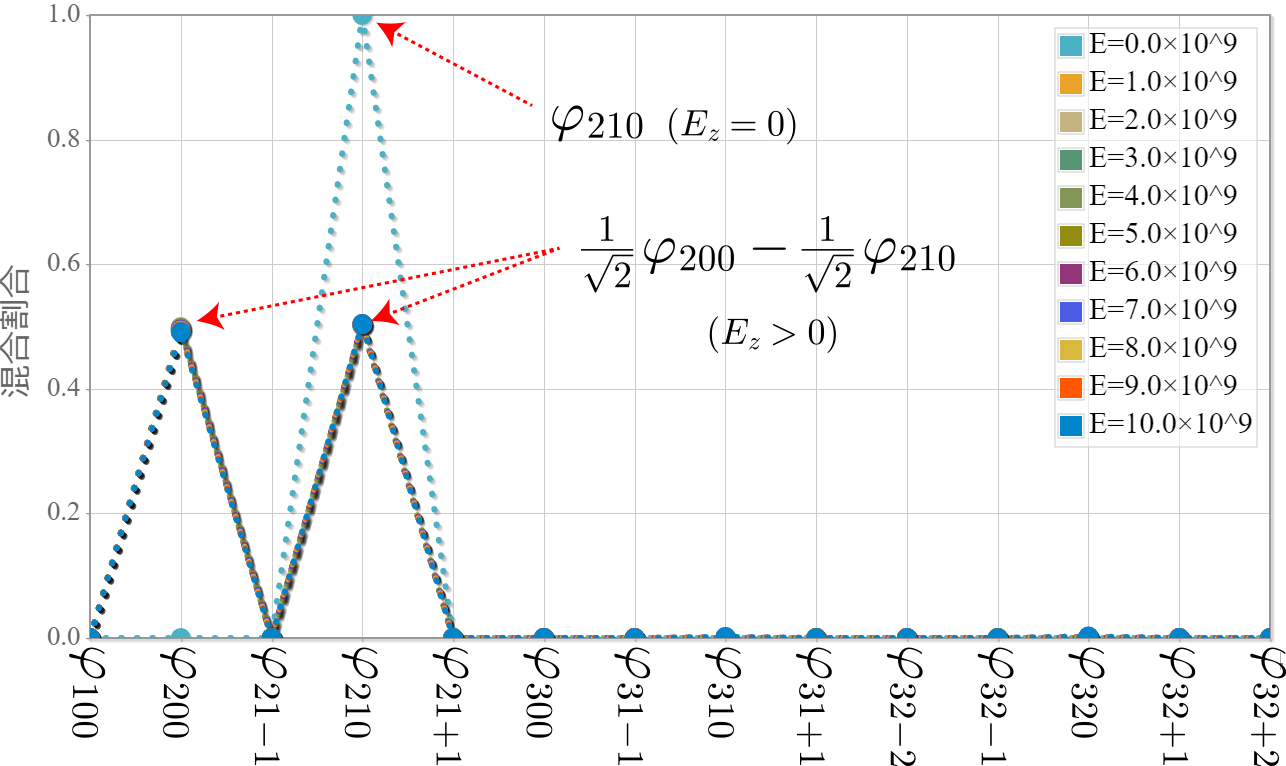
電子の空間分布はさっきと反対になってるね。つまり、もともと存在する電気双極子によって、電場を加えることでエネルギーが高くなる状態と低くなる状態が生み出されることがわかったね。
電気双極子と電場との相互作用で生じるエネルギーシフトは電場に比例するから、１次のシュタルク効果の正体がわかったね！パチパチ！

電場を強くすると。。。

電場を$E_z=1.0\times10^9$から$E_z=10.0\times10^9$まで強くしても、$\varphi_{200}$と$\varphi_{210}$の混合割合はほとんど50%で変化しないけれども、
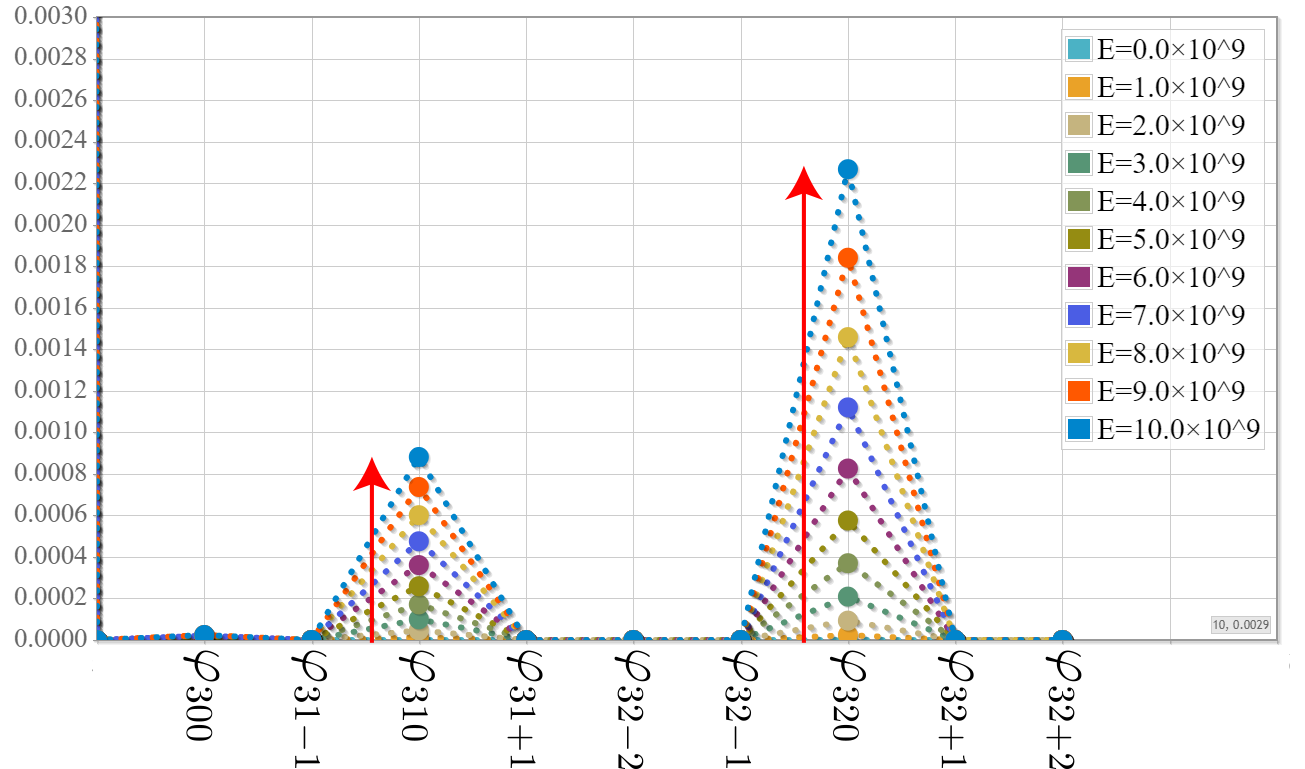
下の図で示したとおり、小さな確率だけれども実はちょっとずつ他の固有状態が混じってくる割合が高くなっていくんだね。
しかも、割合は電場強度に比例せずに、変化の割合は大きくなっているね。これは電場強度をもっともっと強くすると影響が出てきそうだね。

エネルギーが変化しない２重縮退の固有状態をシミュレーション！

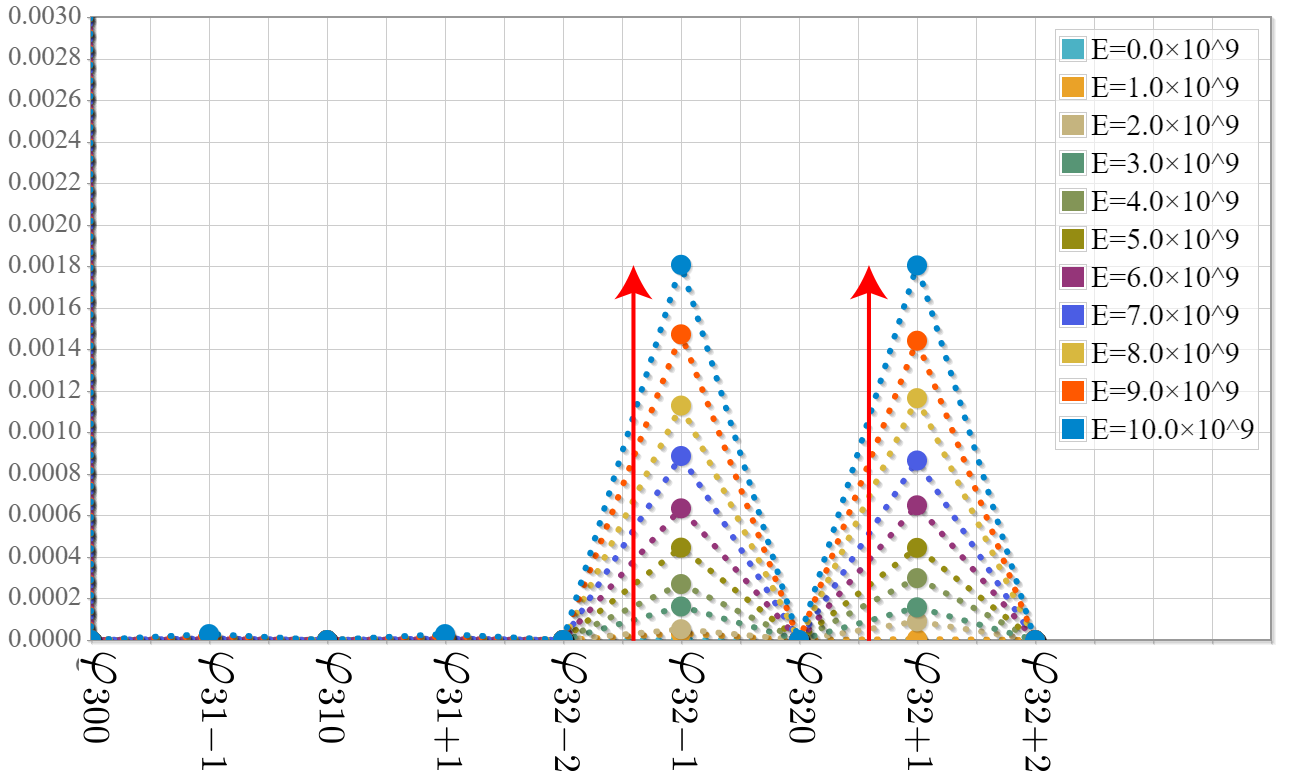
$\varphi_{21+1}$と$\varphi_{21-1}$に電場を加えると、下の図で示すように２つの状態が徐々に混合することがわかったよ。
たまたまだけれども、ちょうど$E_z=10.0\times10^9$でおおよそ50%づつの混合割合になることがわかったよ。

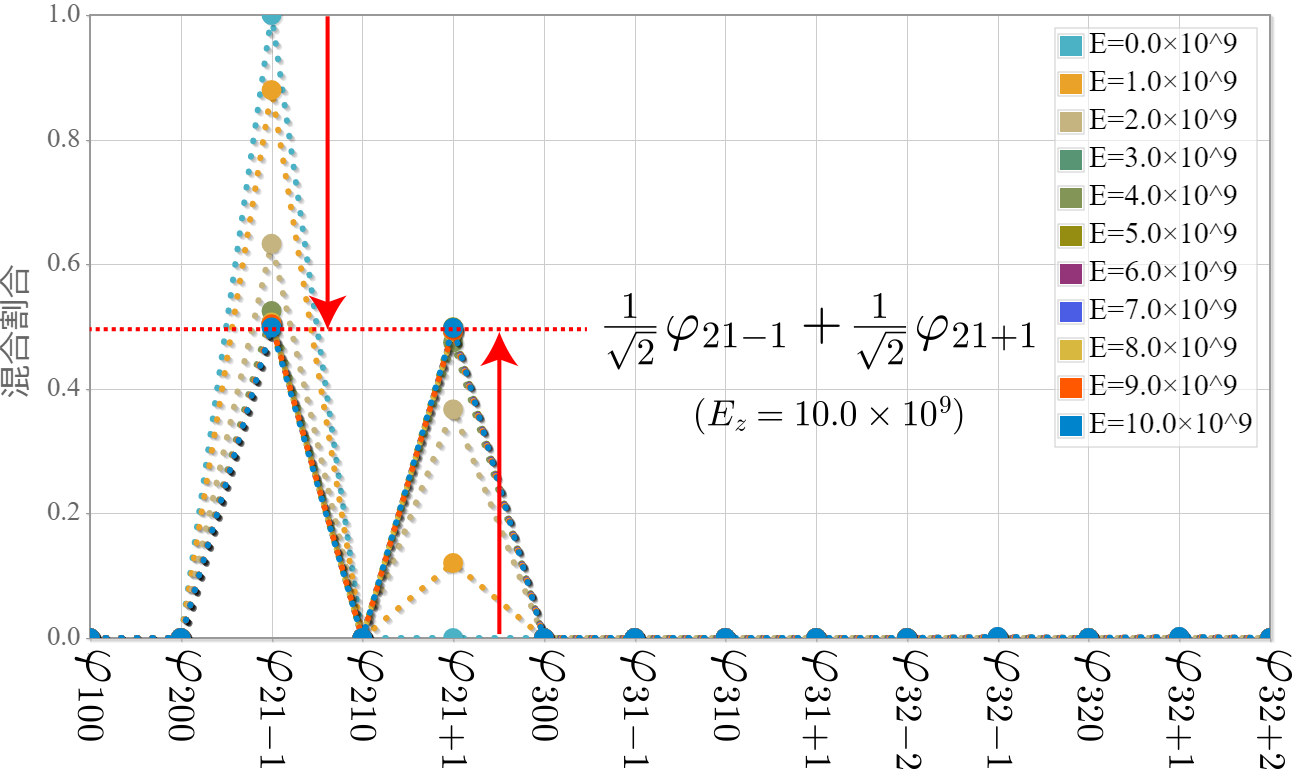
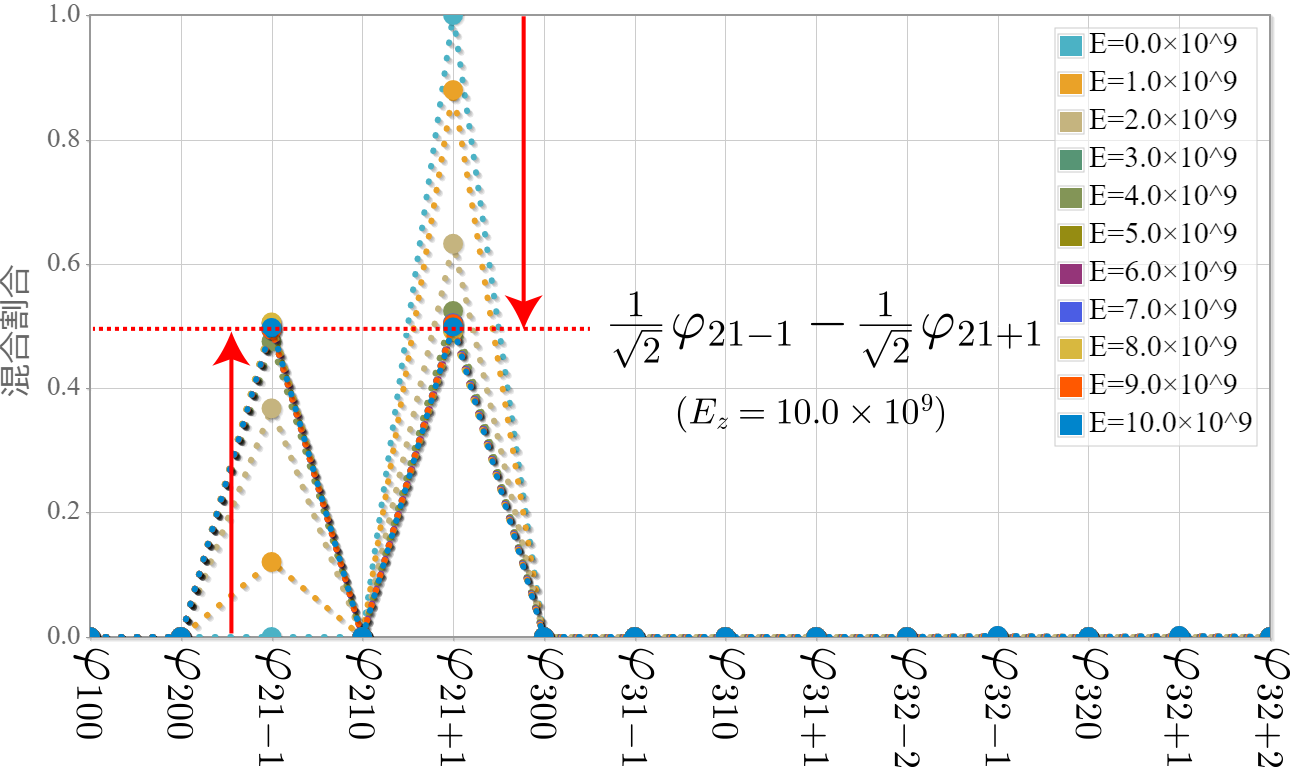
$E_z=1.0\times10^9$の場合と$E_z=10.0\times10^9$の場合の波動関数をそれぞれ見てみよう！

$E_z=1.0\times10^9$のときの固有状態

$E_z=1.0\times10^9$のときの混合割合はおよそ1:9程度だね。x軸上とy軸上がそれぞれ腹になっている感じがわかるね。

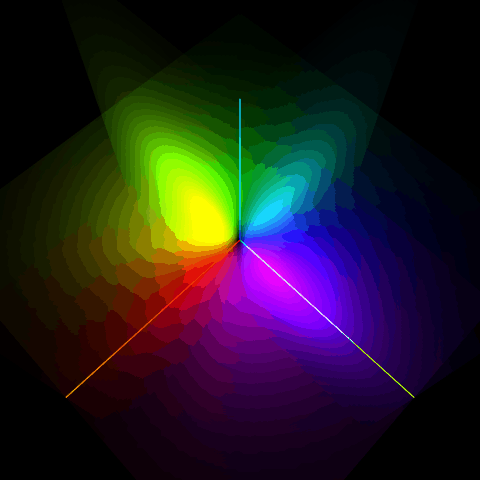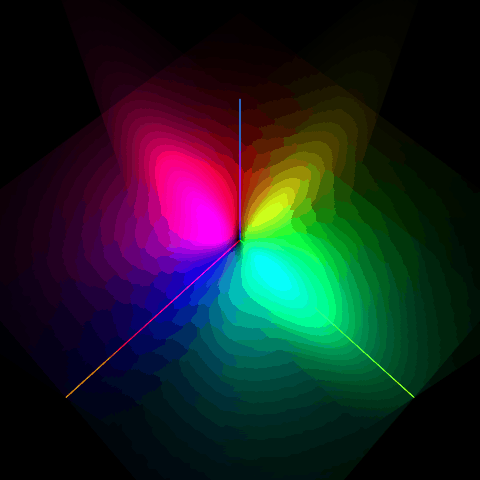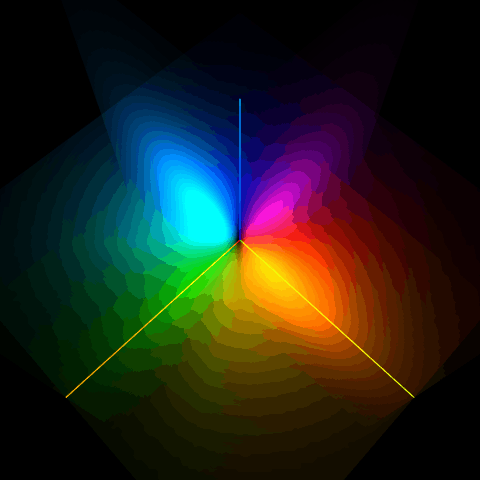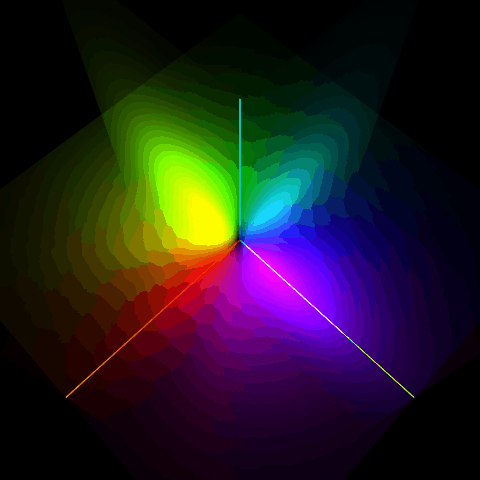
$E_z=10.0\times10^9$のときの固有状態

$E_z=10.0\times10^9$のときの混合割合はほとんど1:1だね。x軸上とy軸上が腹の定常波になっていることがわかるね。それぞれ$p_x$軌道、$p_y$軌道だね。

ちなみにこの状態も電場が強くなるにつれて、僅かだけれどもも下の図で示したように他の状態が少しづつ混合してくよ。

まとめと今後の予定

わかったこと

• 第１励起状態で存在する自発的な電気双極子によって、エネルギーシフトが生じる。
• １次のシュタルク効果の正体は、電気双極子と電場の相互作用！！
• ちょうど$E_z=10.0\times10^9$あたりで、いわゆる$p_x$軌道、$p_y$軌道が固有状態となる

今後の予定

• 電場をもっと強くしたときの変化を調べてみよう！
• １次のシュタルク効果で生じる電気双極子の分極率を調べてみよう！