【量子コンピュータを作ろう！】（２）量子ドットに束縛された電子に静電場を加えたときの固有状態の計算結果（シュタルク効果）

前回、定式化した量子ドットに束縛された電子に静電場を加えたときの固有状態の計算結果を示すよ。量子井戸の横幅は $L = 10 \times 10^9 [{\rm m}]$（ $=10[{\rm nn}]$ ）としているよ。

基底状態と第一励起状態の固有エネルギーの静電場の強度依存性

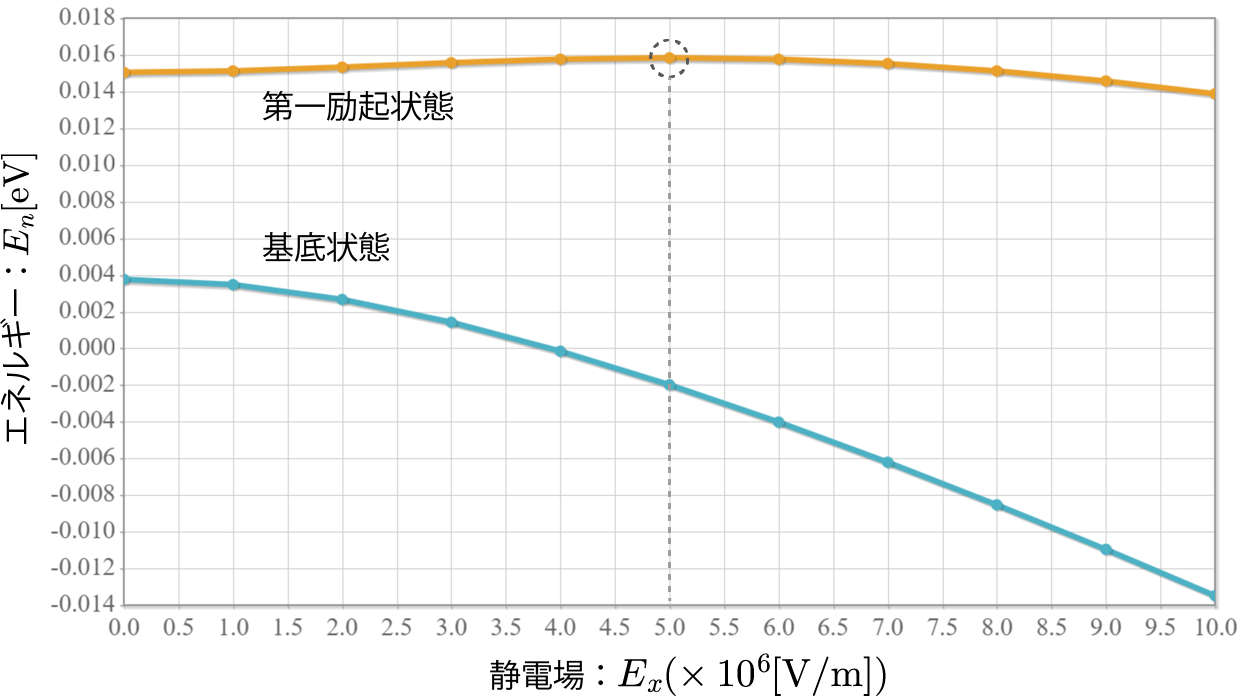
次のグラフは基底状態と第一励起状態の固有エネルギーの静電場の強度依存性だよ。基底状態は電場強度が強くなるにつれてエネルギーが下がっているのに対して、第一励起状態は電場強度が強くなるにつれて初めエネルギーが上がっていった後に下がって行く様子がわかるね。その分岐点となる電場強度はおおよそ $E_x = 5.0\times 10^6 [{\rm V/m}]$ であることがわかるね。静電場が加わることでエネルギーが上下する理由は電気双極子が誘起されていることを意味しているよ。エネルギーが下がるのは電気双極子モーメントが静電場の向きと平行となり、反対に上がるのは電気双極子モーメントが静電場の向きと反平行となっていると考えられるね。

基底状態と第一励起状態の固有関数の静電場強度別の空間依存性

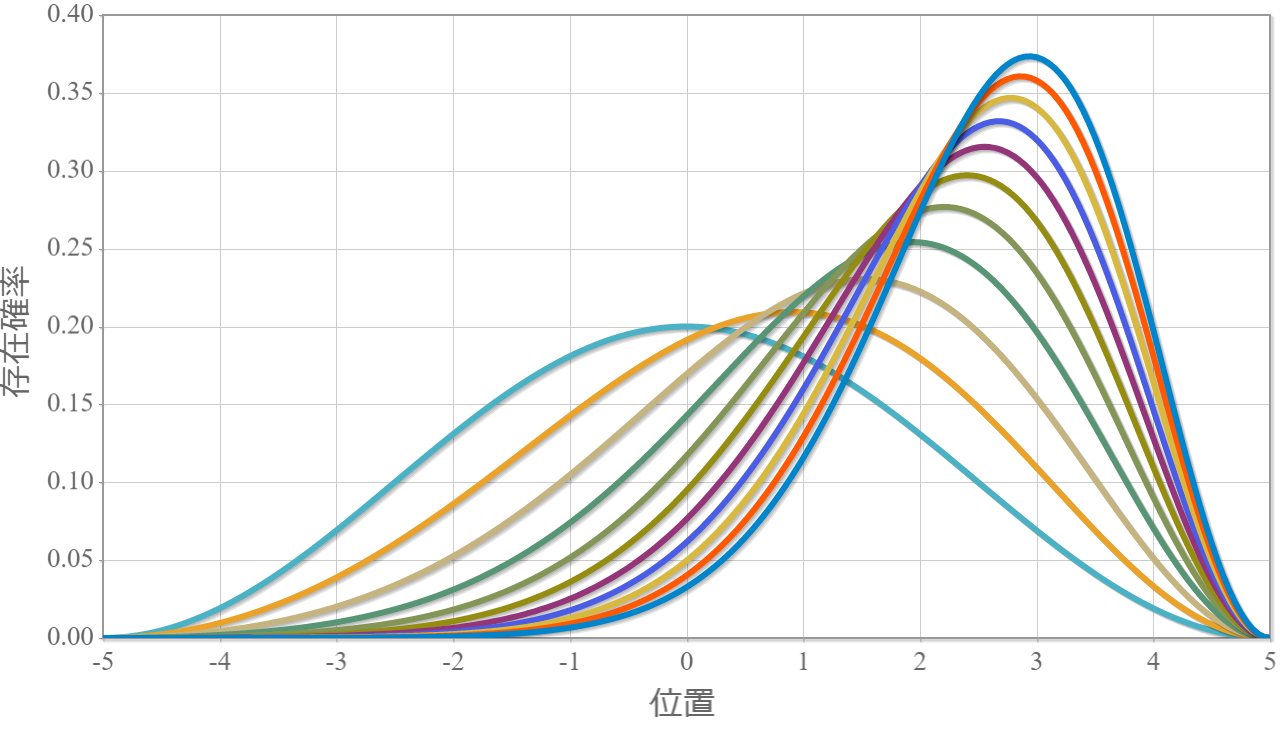
次のグラフは基底状態の固有関数の静電場強度別の空間依存性だよ（$E_x = 0.0\times 10^6 \sim 1.0\times 10^6 [{\rm V/m}]$）。静電場が強くなるほど電子の分布がx軸の正方向に偏っていくね。つまり、電気双極子モーメントが大きくなっていることに対応しているよ。

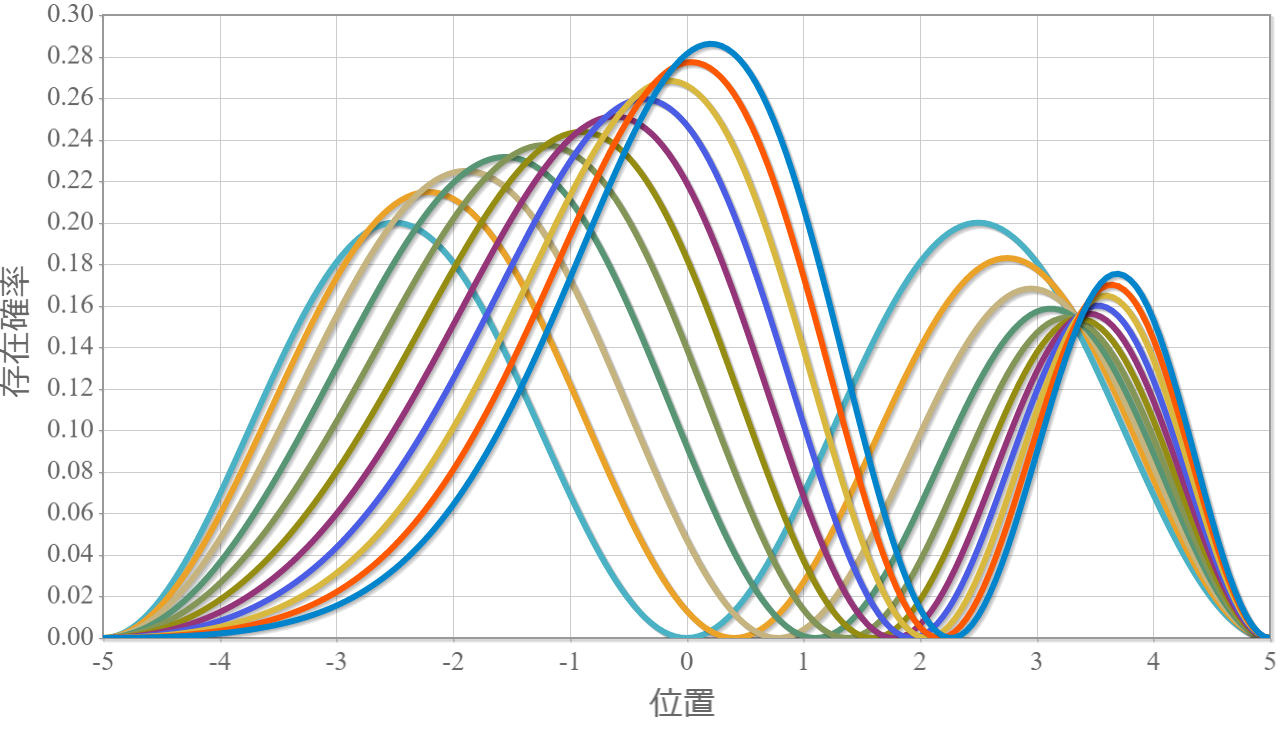
次のグラフは第一励起状態の固有関数の静電場強度別の空間依存性だよ（$E_x = 0.0\times 10^6 \sim 10.0\times 10^6 [{\rm V/m}]$）。第一励起状態はエネルギー準位の電場強度依存性からも分かる通り、$E_x = 5.0\times 10^6 [{\rm V/m}]$ までは、電場強度に応じて電子分布はx軸の負方向に偏っていくね。それよりも大きな電場を加えると、反対にx軸の正方向に偏っていくね。

以上の結果より、外部から静電場を加えることで、基底状態と第一励起状態は異なる向きの電気双極子モーメントが誘起されることがわかったね（シュタルク効果）。これを利用することで、基底状態と第一励起状態の区別をつけることができるよ。次回は、この基底状態と第一励起状態を入れ替えるラビ振動を確かめるよ。