【量子コンピュータを作ろう！】（10）２重量子ドットに束縛された電子に静電場を加えたときの固有状態の計算結果（シュタルク効果）

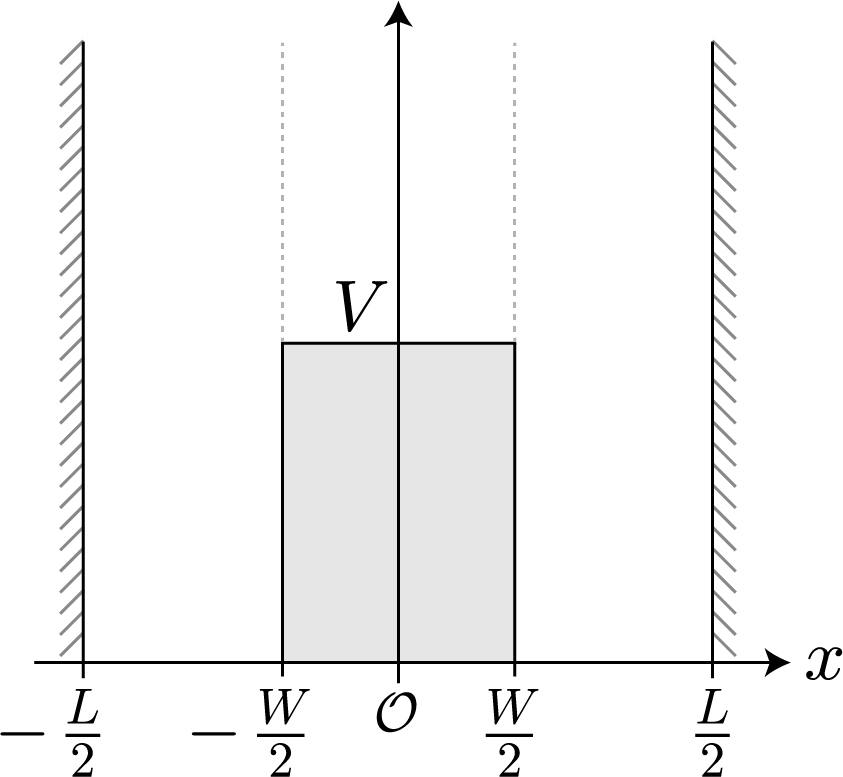
前回計算した２重量子ドットに束縛された電子の固有状態にさらに外部から静電場を加えたときの様子をシミュレーションするよ（静電場の向き：x軸の正方向）。電子分布が偏ってエネルギー準位がシフトするシュタルク効果が期待できるね。２重井戸の場合はどんな形になるのかな。ハミルトニアンのポテンシャル項は次のとおりだよ。

\begin{align}
V(x) = \left\{ \matrix{ \infty & x \leq -\frac{L}{2} \cr e E_x x & -\frac{L}{2} \leq x\leq -\frac{W}{2} \cr V & -\frac{W}{2}
\leq x\leq \frac{W}{2} \cr e E_x x& \frac{W}{2} \leq x\leq \frac{L}{2} \cr \infty & \frac{L}{2} \leq x} \right.
\end{align}

なお、具体的なパラメータとして、量子井戸全体のサイズを $L = 10[{\rm nm}]$、真ん中の壁のサイズを $W = 2[{\rm nm}]$、壁の高さを $0.3[{\rm eV}]$ として、静電場の強さを $0 \sim2.0\times10^{6}[{\rm V/m}]$ と $0.1$ ずつ変化させてみたよ。まずは、固有状態から見てみよう！

固有状態の空間分布

基底状態と第一励起状態

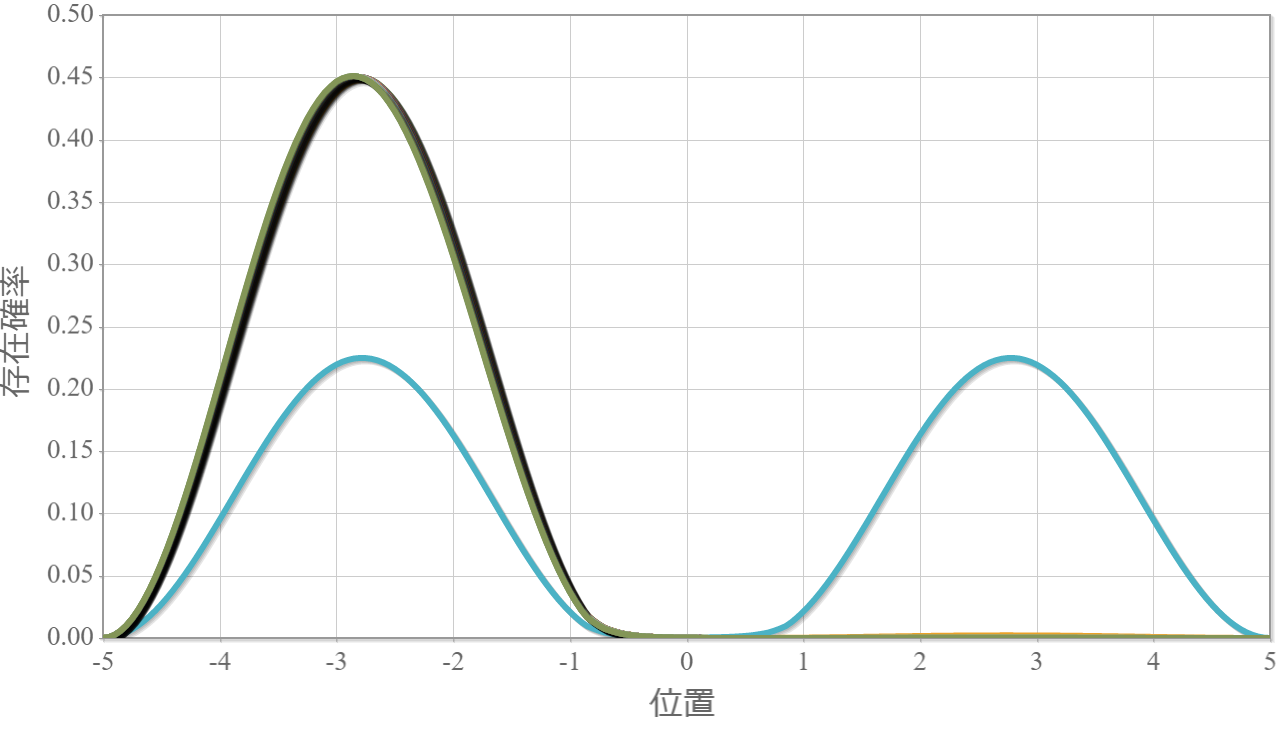
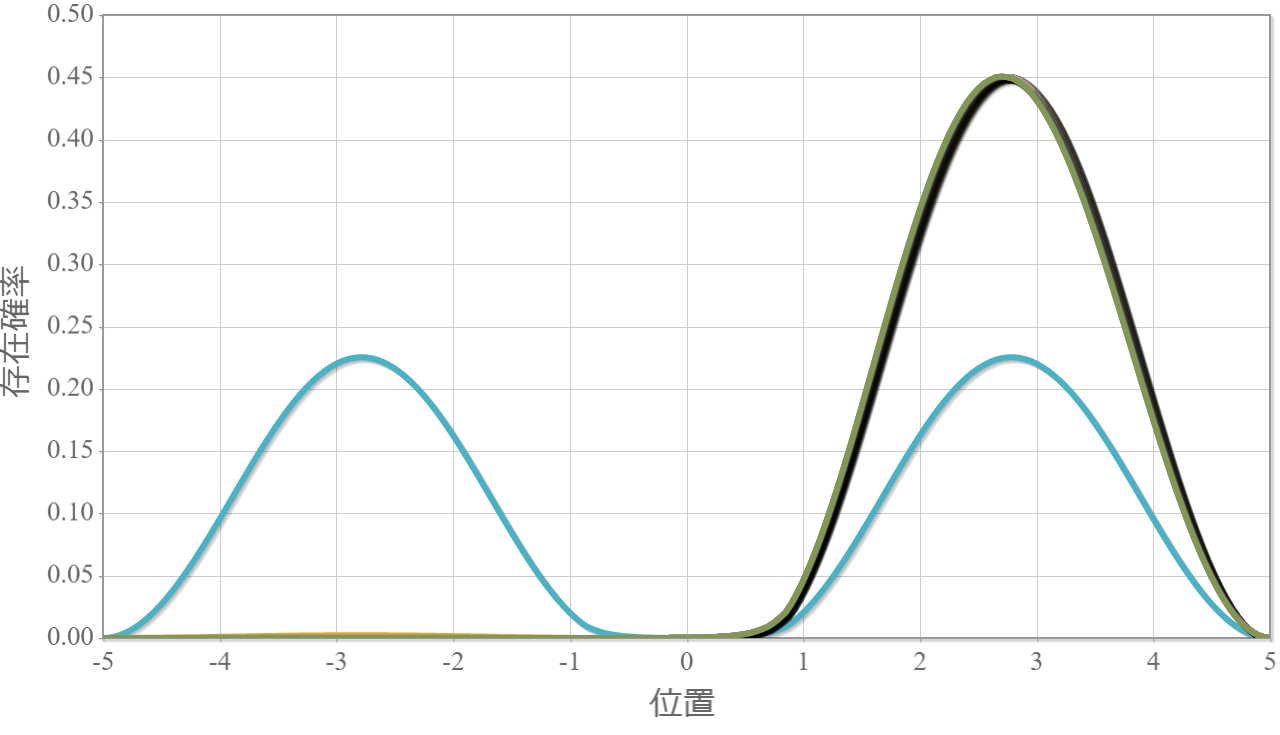
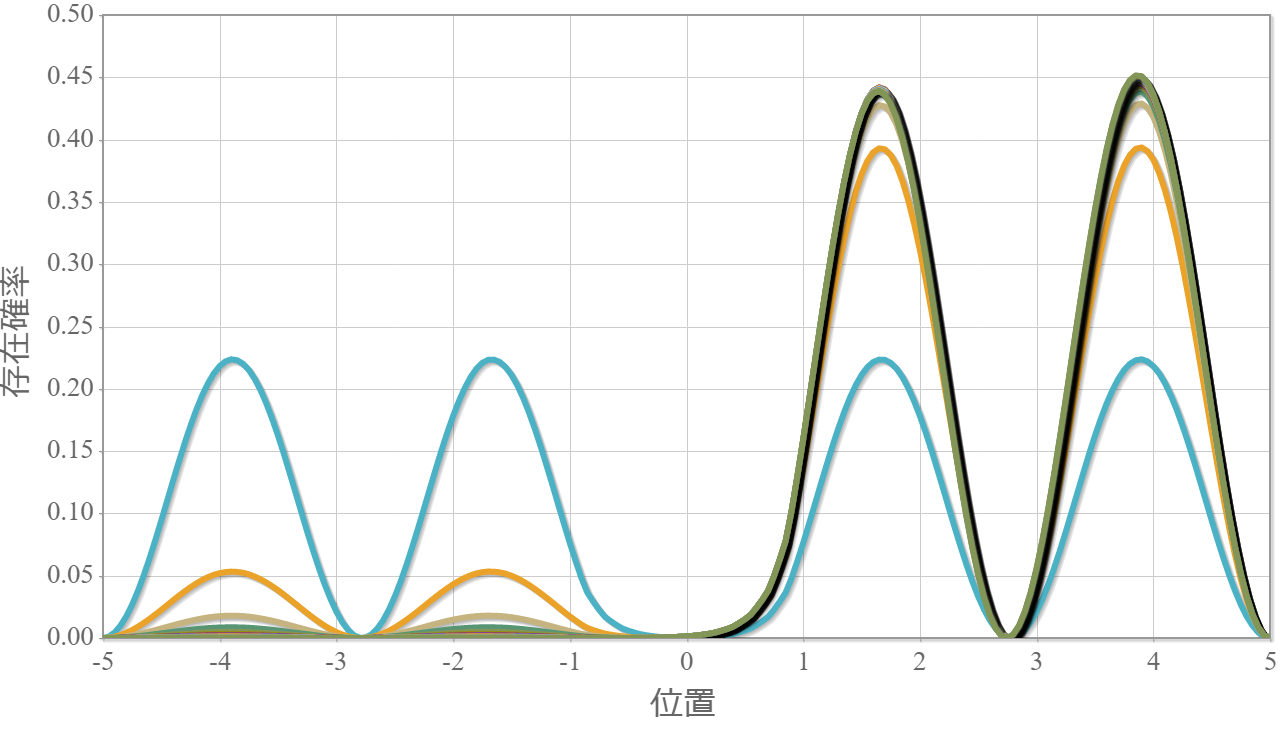
次の図は、静電場の強さを $0 \sim2.0\times10^{6}[{\rm V/m}]$ と $0.1$ ずつ変化させたときの基底状態（左）と第一励起状態（右）の空間分布だよ。静電場を少し加えただけで、電子は片端に偏っているね。ちょっとした外部静電場で電気双極子が生じていると言えるね。興味深いことに、真ん中に壁が無い場合の電気双極子と比較して、かなり弱い電場強度で同等の分極率（100倍）が得られているね（壁無し：$10\times10^{6}$ で基底状態のピーク位置が$2.7[{\rm nm}]$ 程度、壁有り：$0.1\times10^{6}$ でピーク位置が$2.7[{\rm nm}]$ 程度）。特に壁無しの第一励起状態は分極率は小さそうだったので、かなりの差だと言えるね。

第二励起状態と第三励起状態

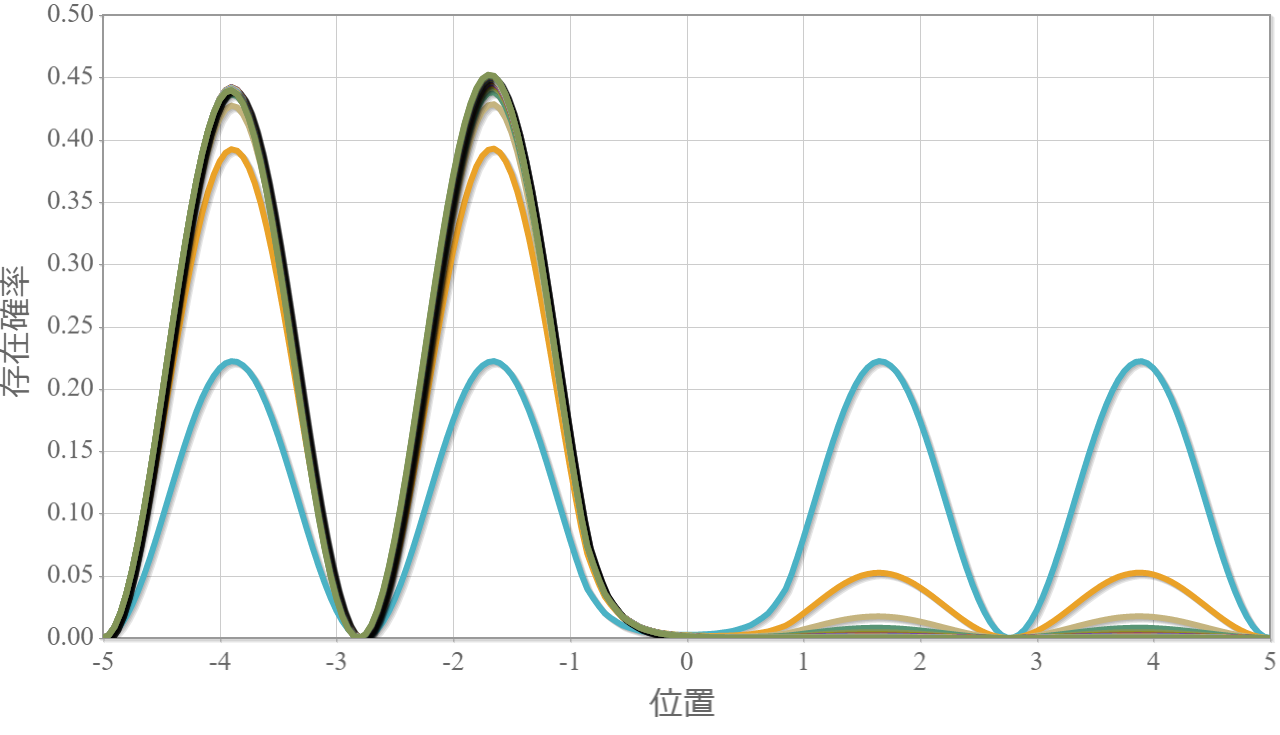
次の図は、静電場の強さを $0 \sim2.0\times10^{6}[{\rm V/m}]$ と $0.1$ ずつ変化させたときの第二励起状態（左）と第三励起状態（右）の空間分布だよ。静電場を $0.3 \times10^{6}[{\rm V/m}]$程度加えただけで、電子は片端に偏っているね。基底状態に対してより強い電場が必要なのは、もともとエネルギーが高い状態だからだね。

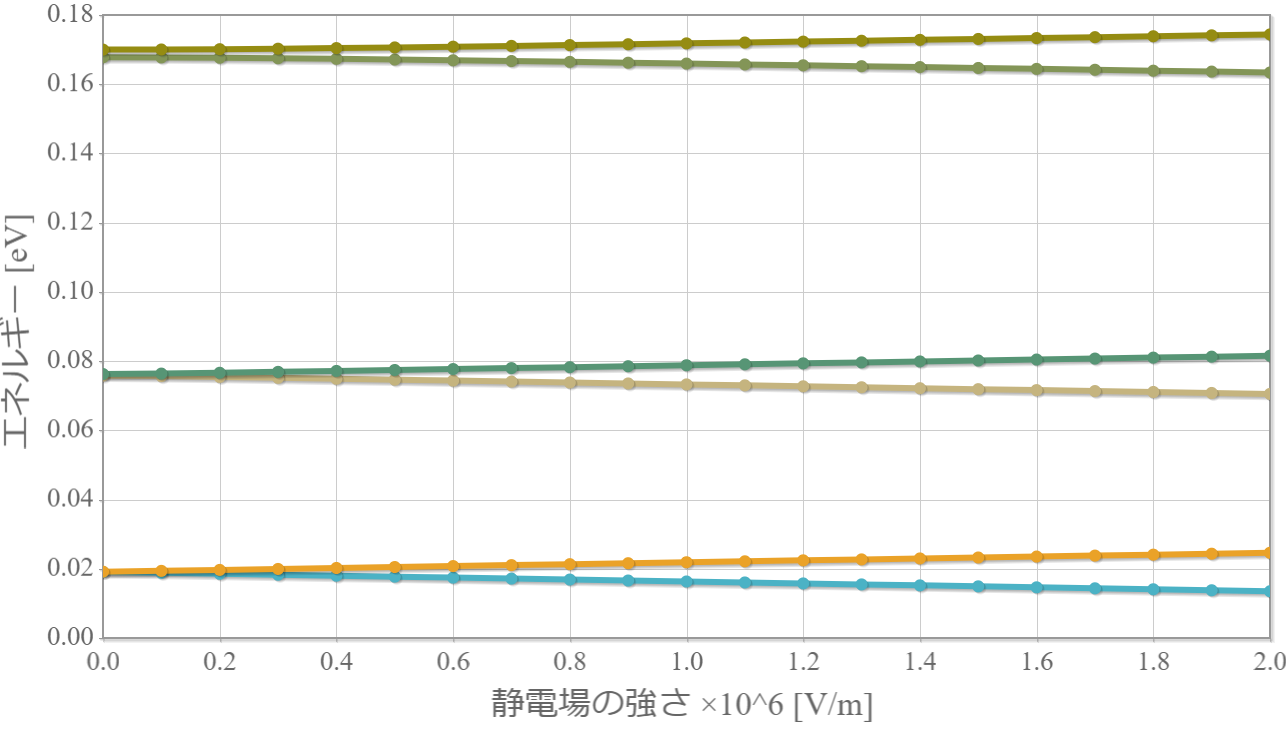
エネルギー準位の静電場依存性

次の図は下から６つのエネルギー準位の壁の高さ依存性だけれども、通常のシュタルク効果と同様、静電場によって縮退している状態が解けて、電場強度に比例した大きさのエネルギーシフトが見られるね。先に示したとおり、僅かな静電場で電気双極子が得られるので、この２重量子井戸をそのまま１量子ビットに用いることで、量子ビット間の相互作用を強めることができる可能性があるね。

次回はいよいよ電子２個に進むよ。まずは１重の量子井戸に２個の電子を束縛したときの固有状態を計算するよ。