【量子コンピュータを作ろう！】（11）量子ドットに束縛された電子2個に対するハミルトニアンと計算方法（失敗）

今回から２量子ビットを作るための方法を考えていくね。本稿ではその第一歩として１個の量子ドットに２個の電子を投入したときの固有状態を計算するための計算方法を解説するよ。電子のようにスピンが1/2の粒子が複数個存在する場合、スピン座標を含めて波動関数の座標を交換すると反対称（符号が反転）することが知られているよ（ディラック方程式より）。スピンが1/2の電子のような粒子は、スピン演算子の特定成分の固有値が $\pm\hbar/2$ の２つのなるので、$+$ 符号を上向き、$-$ 符号を下向きと表すことが多いいね。２個の粒子のスピンが同じ向き（平行スピン）の場合には波動関数全体で反平行になる必要があるので空間部分は反対称になるのに対して、２個の粒子のスピンが反対向き（反平行スピン）の場合には空間部分は対称になる必要があるね。１粒子の波動関数をこれまでと同じ

\begin{align}
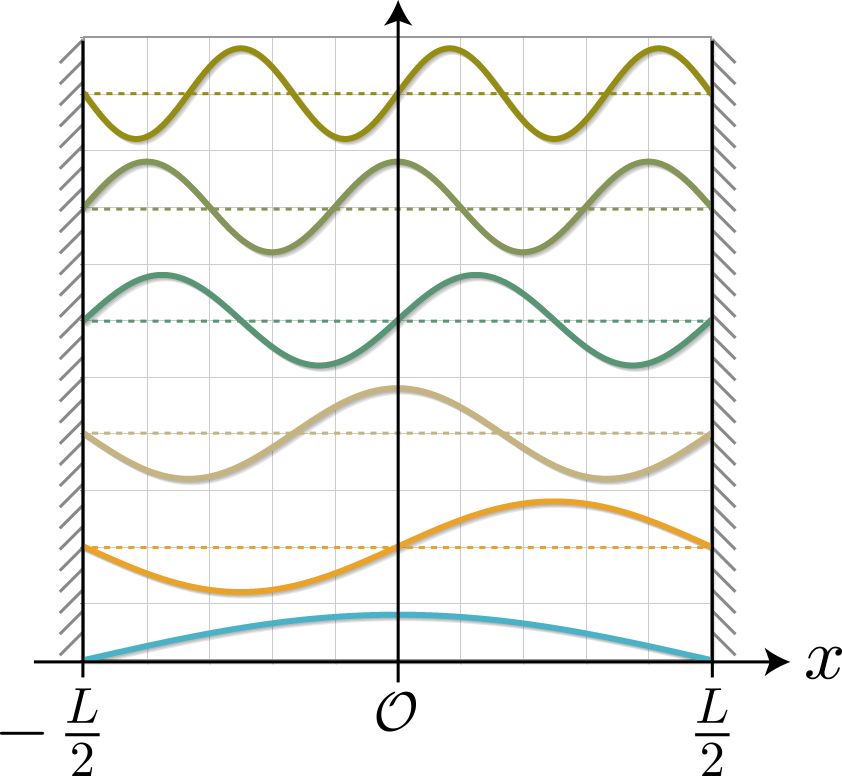
\varphi_n(x) = \sqrt{\frac{2}{L}} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ E^{(0)}_n = \frac{\hbar^2 k_n^2}{2m_e} \ , \ k_n = \frac{\pi(n+1)}{L}
\end{align}

と表した場合、２個の電子の空間対称関数（$\varphi^{(S)}$）と空間反対称関数（$\varphi^{(A)}$）は２つの電子位置を $x_1$ と $x_2$ として、それぞれ次のように表されるよ。

\begin{align}
\varphi^{(S)}_{n_1n_2}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1}(x_1)\varphi_{n_2}(x_2) + \varphi_{n_1}(x_2)\varphi_{n_2}(x_1) \right]\\
\varphi^{(A)}_{n_1n_2}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1}(x_1)\varphi_{n_2}(x_2) – \varphi_{n_1}(x_2)\varphi_{n_2}(x_1) \right]
\end{align}

空間対称関数の場合、$x_1$ と $x_2$ を入替えても変化しないのに対して、空間反対称関数の場合、座標を入替えると符号がマイナスになるね。ただし、$n_1 = n_2$ の場合、空間対称関数の場合の係数は $1$ とする必要があることと、反対称関数の場合には関数値が $0$ になることに注意が必要だね。もし２個の電子が相互作用をしない場合、基底状態は空間対称関数（反平行スピン）で $n_1=n_2=0$ の場合だね。

\begin{align}
\varphi^{(S)}_{00}(x_1,x_2) = \varphi_{0}(x_1)\varphi_{0}(x_2)
\end{align}

第一励起状態は空間反対称関数（平行スピン）で $n_1=1, n_2=0$ あるいは $n_1=0, n_2=1$ の場合だね。

\begin{align}
\varphi^{(A)}_{10}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{1}(x_1)\varphi_{0}(x_2) – \varphi_{0}(x_2)\varphi_{1}(x_1) \right]\\
\varphi^{(A)}_{01}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{0}(x_1)\varphi_{1}(x_2) – \varphi_{1}(x_2)\varphi_{0}(x_1) \right]
\end{align}

両者とも単に符号が反転しているだけなので、同じ関数を表しているよ。

電子間のクーロン力を考慮した場合のハミルトニアンと固有状態の計算方法

電子は同符号の電荷を持っているので互いに反発するね。そのため、基底状態は先に示したような簡単な形にはならないね。クーロン力を考慮した場合の２個の電子に対するハミルトニアンは次のとおりだよ。

\begin{align}
\hat{H} = \hat{H}_1 + \hat{H}_2 + V(|x_1-x_2|)= -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_1^2} -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_2^2} + \frac{1}{4\pi\epsilon_0} \, \frac{1}{|x_1 – x_2|}
\end{align}

前の２項はそれぞれの電子の運動エネルギー、最後の項は相互作用を表しているね。このハミルトニアンの固有関数を $\psi^{(S)}(x_1, x_2)$（空間対称関数）、$\psi^{(A)}(x_1, x_2)$（空間反対称関数）と表した場合のシュレディンガー方程式は

\begin{align}
\hat{H} \psi^{(S)}(x_1, x_2) &\ = E \psi^{(S)}(x_1, x_2) \\
\hat{H} \psi^{(A)}(x_1, x_2) &\ = E \psi^{(A)}(x_1, x_2)
\end{align}

だね。この $\psi(x_1, x_2)$ は正規直交系である $\varphi^{(S)}_{n_1n_2}$ あるいは $\varphi^{(A)}_{n_1n_2}$ で展開できるはずなので、次のように表すことができるよ。

\begin{align}
\psi^{(S)}(x_1, x_2) &\ = \sum\limits_{n_1,n_2} a_{n_1n_2}\, \varphi^{(S)}_{n_1n_2}(x_1, x_2) \\
\psi^{(A)}(x_1, x_2) &\ = \sum\limits_{n_1,n_2} a_{n_1n_2}\, \varphi^{(A)}_{n_1n_2}(x_1, x_2)
\end{align}

ちなみに空間対称関数と反対称関数は直交するため混じり合うことは無いよ。ここからはいつもの常套手段でいくよ。この固有関数をハミルトニアンに代入して、両辺に $\varphi^{(S)*}_{n_1n_2}(x_1, x_2)$ あるいは $\varphi^{(A)*}_{m_1m_2}(x_1, x_2)$ を掛け算して全空間で積分すると

\begin{align}
a_{m_1m_2} ( E_{n_1}^{(0)} + E_{n_2}^{(0)}) + \sum\limits_{n_1,n_2} \langle m_1m_2|V(|x_1-x_2|)| n_1 n_2 \rangle a_{n_1n_2} = E a_{m_1m_2}
\end{align}

となるね。これは展開係数 $a_{m_1m_2}$ についての連立方程式となっているよ。対称性と反対称性の違いはブラ・ケット表記で表した積分

\begin{align}
\langle m_1m_2|V(|x_1-x_2|)| n_1 n_2 \rangle a_{n_1n_2} \equiv \left\{ \matrix{ \int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^{(S)*}_{m_1m_2}(x_1, x_2) V(|x_1-x_2|) \varphi^{(S)}_{n_1n_2}(x_1, x_2)dx_1dx_2 \cr \int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^{(A)*}_{m_1m_2}(x_1, x_2) V(|x_1-x_2|) \varphi^{(A)}_{n_1n_2}(x_1, x_2)dx_1dx_2 } \right.
\end{align}

に違いが現れるね。次回は実際に固有状態を計算するよ。

追記：2019.07.16

同じ量子井戸に２個の電子を配置する場合、上記のような展開では積分が発散してしまうため、計算不能となってしまうね。発散を抑えられる正規直交展開にしないといけないけれども、どうしてもうまくいかないので、この方法は一度断念するね。