タグ: シュレディンガー方程式

独立電子近似の場合、ヘリウム原子の２つの電子の波動関数は、個々の水素様原子（ $Z=2$ ）の波動関数の積を用いて、空間対称（スピン３重項／パラ）あるいは空間反対称（スピン１重項／オルト）の２つの状態をとるよ。具体的な波動関数の表式はそれぞれ

\begin{align}
\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) + \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) – \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\end{align}

と表されるね。この波動関数は各粒子ごとに３次元で合計で６次元の関数なので、これを描画するには工夫が必要になるよ。１番基本的な考え方は、空間位置 $ \boldsymbol{r} $ に粒子１あるいは粒子２が存在する空間確率密度を

\begin{align}
\rho( \boldsymbol{r} ) = \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}) |^2 dV_1 + \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, \boldsymbol{r}_2) |^2 dV_2
\end{align}

と定義することで、空間分布を計算することができるね。ただし、これを先の $\chi^{(S)}$ と $\chi^{(A)}$ に適用すると、

\begin{align}
\rho^{(S)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2\\
\rho^{(A)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2
\end{align}

となって、それぞれの粒子の空間分布の和となるね。ヘリウム原子の低エネルギーの状態は、粒子の片方は必ず $(n,l,m)=(1,0,0)$ に存在するので、先の空間確率密度を数値的に計算すると、他方の粒子がどの準位に存在したとしても、 $|\varphi_{100}(\boldsymbol{r})|^2 >> |\varphi_{nlm}(\boldsymbol{r})|^2 $ となって、実質的に $|\varphi_{100}(\boldsymbol{r})|^2$ となってしまうね。これは、２つの粒子が存在する確率が $|\varphi_{100}(\boldsymbol{r})|^2$ で表される領域に集中していることを意味しているよ。

そこで今回は、粒子の１つが $\varphi_{100}(\boldsymbol{r})|$の最も確率の高い原点（ $\boldsymbol{r}_1=0$ あるいは $\boldsymbol{r}_2=0$ ）に存在するとして、他方の粒子の空間確率密度

\begin{align}
\rho^{(S)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, 0)|^2 \\
\rho^{(A)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r},0)|^2
\end{align}

を定義して、空間分布を描画したよ。ちなみに両者とも第１項目と第２項目の値は同じ値となるよ。

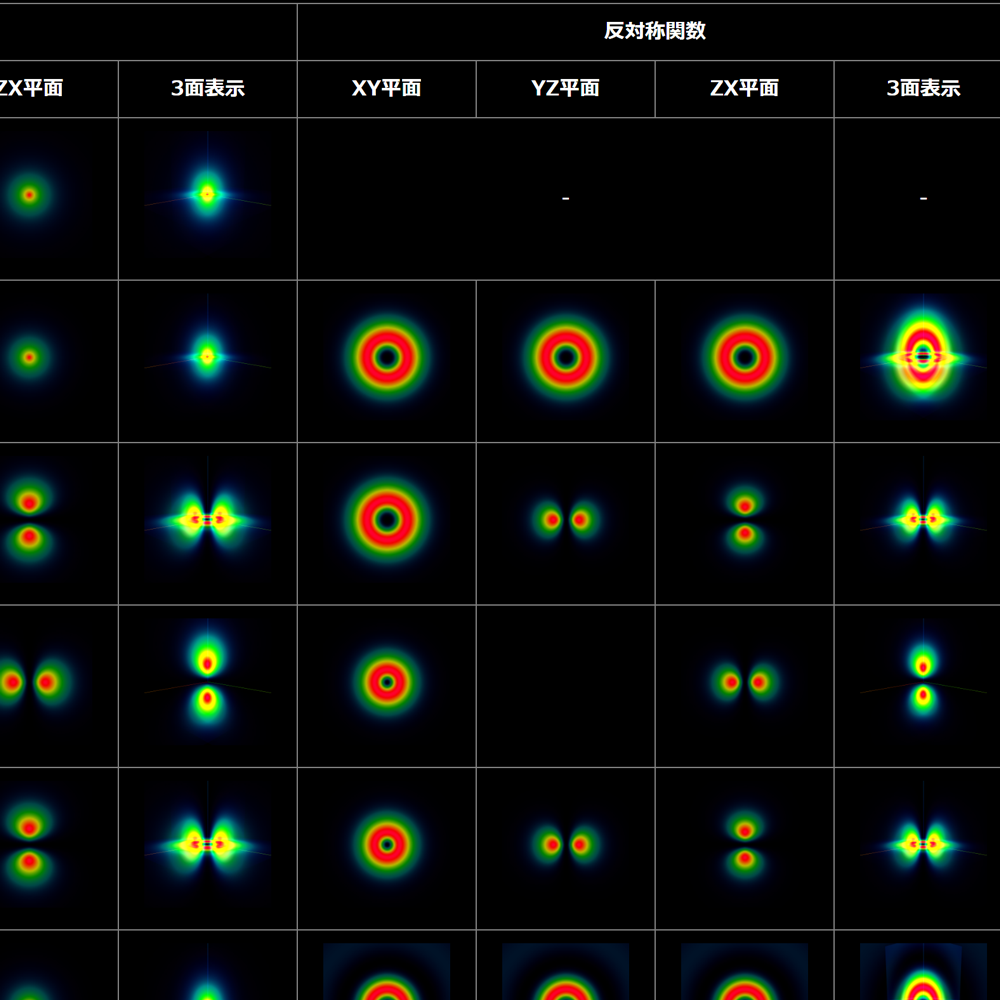
（※実際の表はこちらのページを見てね！）

上記の結果は単に $|\varphi_{nlm}(\boldsymbol{r})|^2$ を計算した結果に似ているけれども異なるよ。空間対称関数と空間反対称関数では、概ね同じだけれども顕著に異なるのが、２個目の粒子の状態が $(n,l,m) =(2,0,0)$ や $(n,l,m) =(3,0,0)$ で、原点を中心に存在する場合だね。これは、空間対称関数の場合には、同じ領域に居ようとするけれども、空間反対称関数の場合には、互いに避けようとする結果だね。次回は、電子間の相互作用を加味した波動関数を描画するよ。

前回解説した水素原子に静電場を急激に加えたときの緩和時間シミュレーションの結果を示すよ。次の図は初期状態として $\varphi_{200}$ 100%の状態に $ E_z = 10^{9}[\rm{V/m}]$ の静電場を急に加えたときの $\varphi_{200}$ と $\varphi_{210}$ の存在確率の時間経過だよ。$\varphi_{200}$ 100%の状態と $\varphi_{210}$ 100%の状態が一定の周期で交互に現れるね。

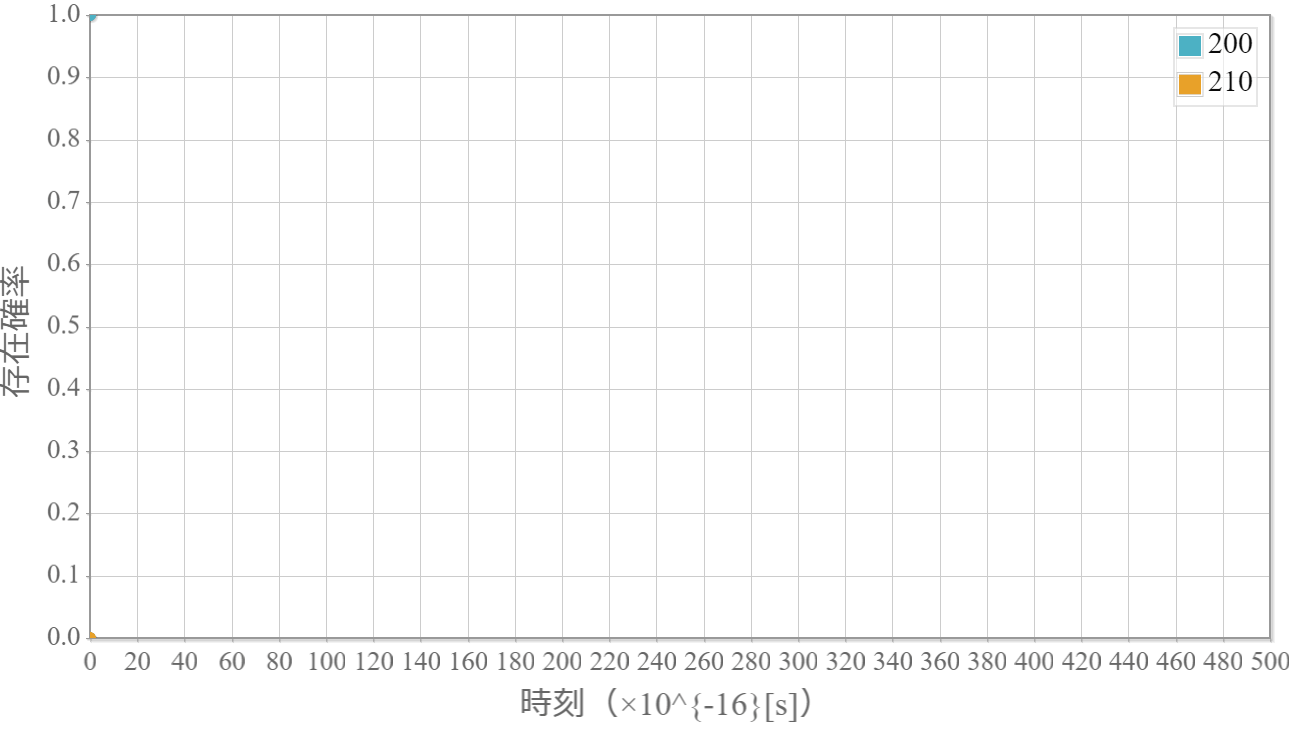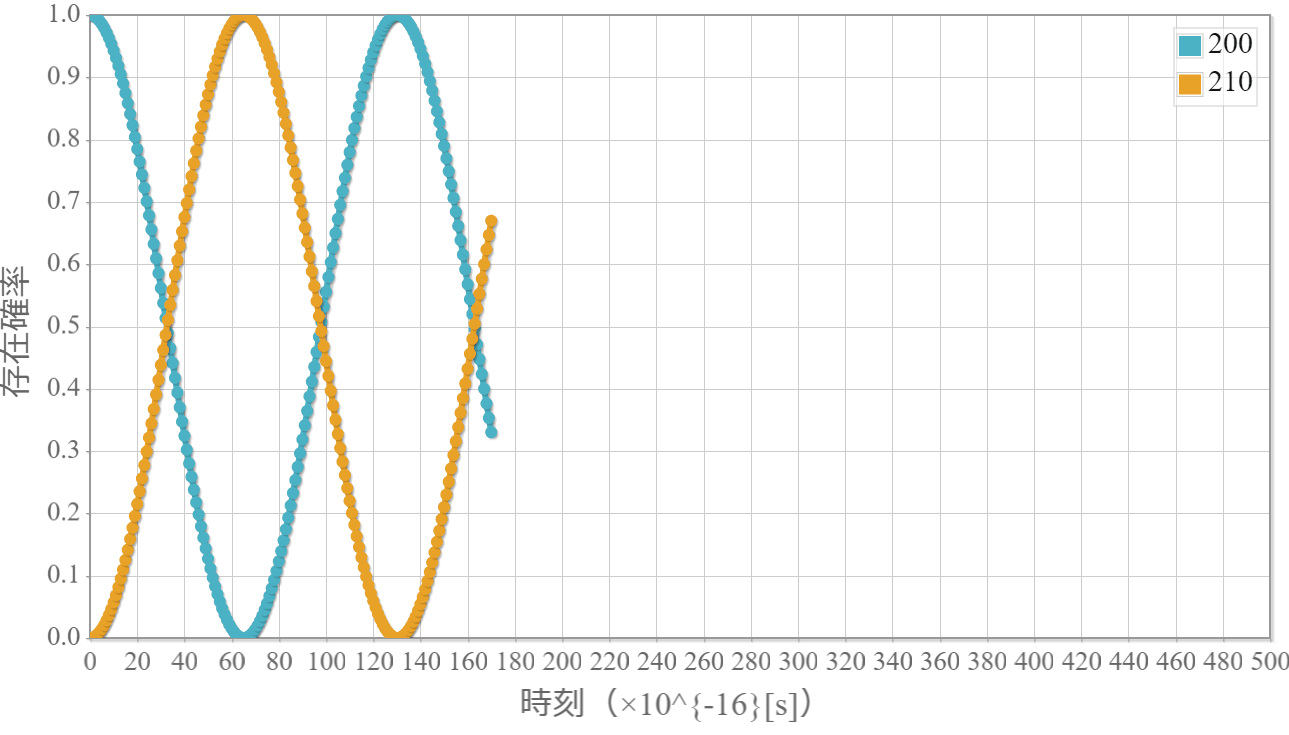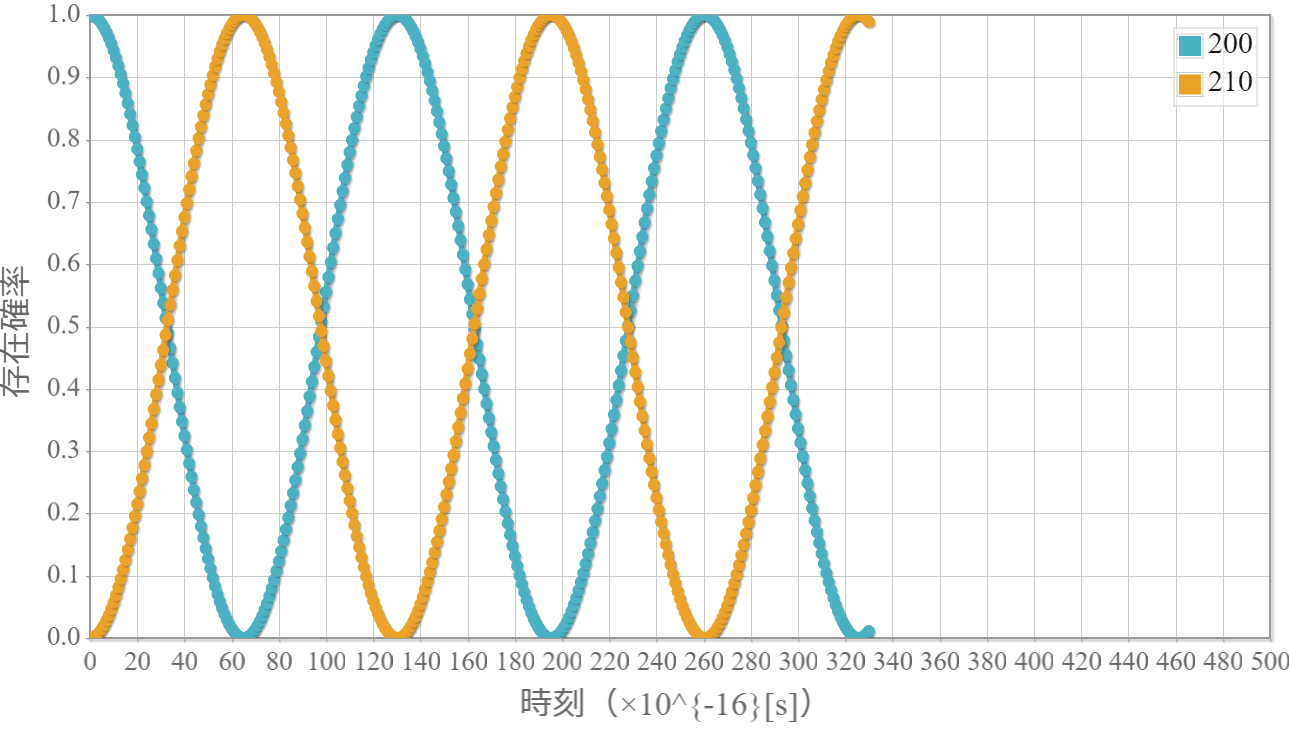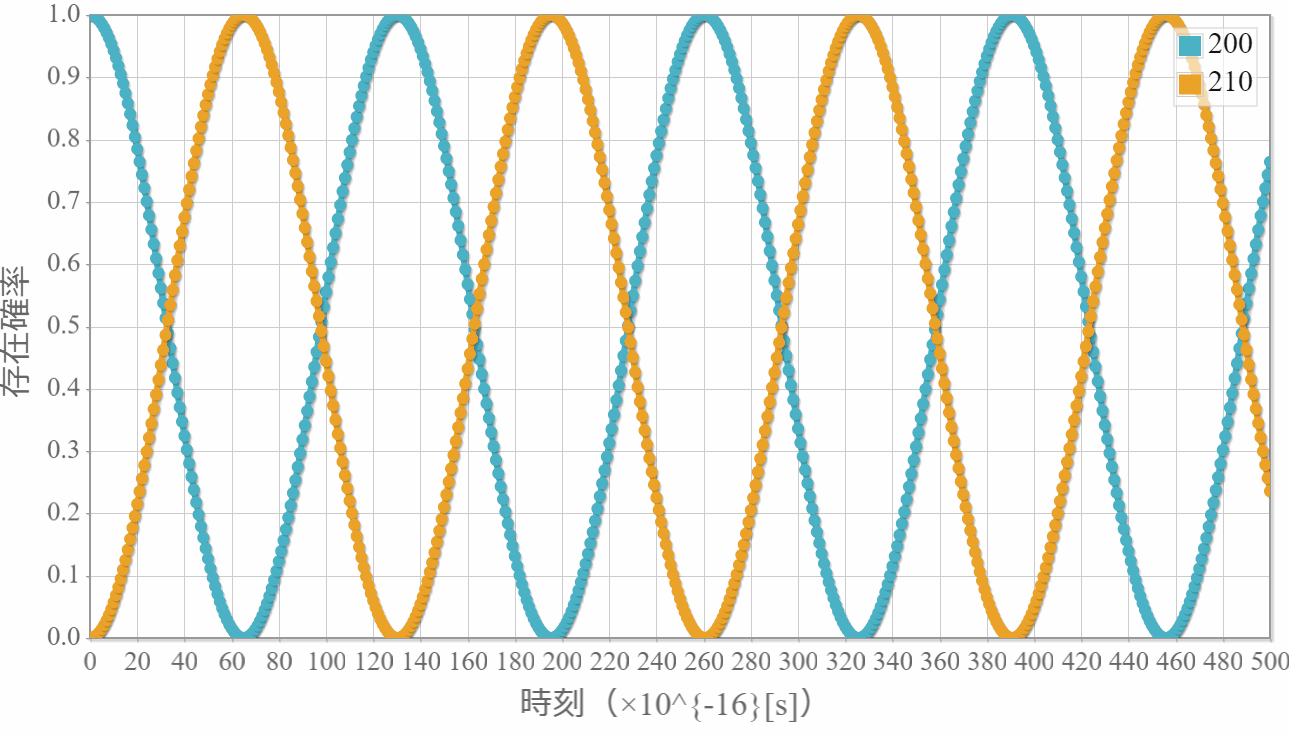
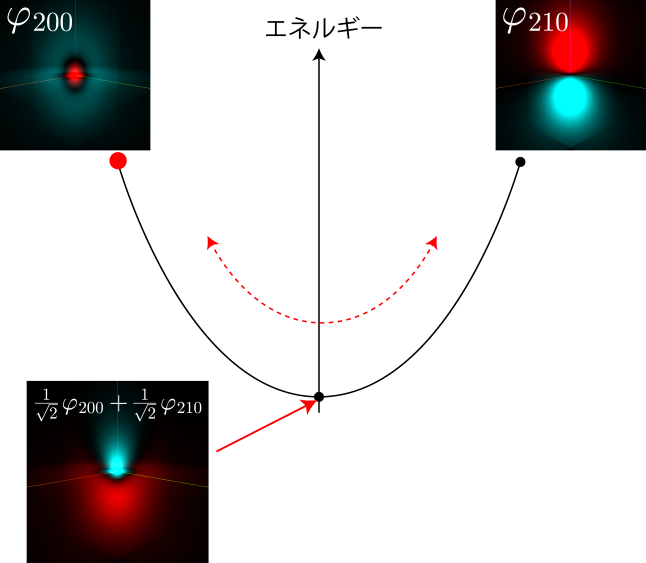
考察：単振動的な運動をする理由

$\varphi_{200}$ と $\varphi_{210}$ は静電場中ではエネルギーが高い一方で、その50%づつの混合状態が一番エネルギーが低いのだよね。つまり、下の図で示したとおり、エネルギーの高い初期状態 $\varphi_{200}$ 100% からスタートして、エネルギー低い方に状態が変化して行くけれども、一番低いところで止まらずに反対の $\varphi_{210}$ 100% の状態まで変化していっているね。もし、エネルギーが散逸するメカニズムがあれば、最低エネルギーに落ち着くよね。きっと。

水素原子に電磁波を加えるシミュレーションの前に、数値計算の確認を兼ねて、水素原子に静電場を急激に掛けたときの緩和時間をシミュレーションしてみるよ。水素原子に静電場を加えた場合、電場によって固有関数が歪むシュタルク効果を以前解説したね。今回は、時刻 $t<0$ では外場無しの状態から、$t\geq0$ で急に $V_0$ の電場を加えたときの状態変化の様子をシミュレーションするよ。数値計算の手順をいかに解説するね。ハミルトニアンを外場無しと時間に依存するポテンシャル項に分けるね。

\begin{align}
\hat{H} = \hat{H}_0 + \hat{V}(\boldsymbol{r}, t)
\end{align}

$\hat{V}(t)$ を次の通りとするよ（電場の向きをz軸方向とするね）。

\begin{align}
\hat{V}(\boldsymbol{r}, t) = \left\{ \matrix{ 0 & (t<0) \cr eE_zz & (t\geq 0)} \right. \end{align}

時刻 $t$ の波動関数を $\Psi(\boldsymbol{r}, t) $ を外場無しの場合の固有状態 $\varphi_{nlm}$ で展開して、展開係数が時間に依存すると考えるよ。

\begin{align}
\Psi(\boldsymbol{r}, t) = \sum\limits_{nlm} a_{nlm}(t) \varphi_{nlm}(\boldsymbol{r})
\end{align}

これを元のシュレディンガー方程式 $i\hbar \frac{\partial}{\partial t} \Psi(\boldsymbol{r}, t) = \hat{H} \Psi(\boldsymbol{r}, t) $ に代入して、両辺に $\varphi_{n’l’m’}^*$ を掛けて全空間で積分するよ。

\begin{align}
i\hbar \frac{d a_{n’l’m’}(t)}{dt} = E_{n’} a_{n’l’m’}(t)+ \sum\limits_{nlm} a_{nlm}(t) \int \varphi_{n’l’m’}^* \hat{V}(\boldsymbol{r}, t) \varphi_{nlm}dV
\end{align}

ちょっと整理して、

\begin{align}
\frac{d a_{n’l’m’}(t)}{dt} = \frac{1}{ i\hbar } \left[E_{n’} a_{n’l’m’}(t) + \sum\limits_{nlm} V^{n’l’m’}_{nlm}(t)\, a_{nlm}(t) \right]
\end{align}

という形をしているね。つまり、$a_{n’l’m’}(t)$ の時間変化は、その時刻の全固有状態の展開係数の値 $a_{nlm}(t)$ と、ポテンシャル積分項の値から計算できることを意味しているね。このポテンシャル積分項の具体的な表記は

\begin{align}
V^{n’l’m’}_{nlm}(t) \equiv \int_0^\infty\!\!\! r^2 dr \int_0^\pi \!\!\! \sin\theta d\theta \int_0^{2\pi} \!\!\! d\phi \left[\varphi_{n’l’m’}^* \hat{V}(\boldsymbol{r}, t)\,\varphi_{nlm} \right] = \left\{ \matrix{ 0 & (t<0) \cr eE_z \int_0^\infty\!\!\! r^2 dr \int_0^\pi \!\!\! \sin\theta d\theta \int_0^{2\pi} \!\!\! d\phi \left[\varphi_{n'l'm'}^* z\,\varphi_{nlm} \right] & (t\geq 0)} \right. \end{align}

となるね。このポテンシャル積分項を用いて、先の $ a_{n’l’m’}(t) $ の常微分方程式を数値的に計算すれば良いね。次回は実際にルンゲ・クッタ法を用いて、緩和時間をシミュレーションしてみるよ。

水素原子核の周りを運動する電子のエネルギー

水素原子核の周りを運動する電子のシュレディンガー方程式から導かれる固有方程式は次のとおりだったよね。

\begin{align}
\hat{H} \varphi_{nlm} = E_n \varphi_{nlm}
\end{align}

$\hat{H}$はハミルトニアン、$\varphi_{nlm}$は固有関数で、$E_n$はエネルギー固有値で

\begin{align}
E_n=- \frac {\hbar ^2}{2m_ea_B^2}\, \frac{1}{n^2} \simeq – \frac{13.6}{n^2}[\rm eV]
\end{align}

の値を取るんだったよね。この式からもわかるとおり、エネルギーは主量子数$n$にしか寄らないから、方位量子数、磁気量子数が違っていても同じ値になるんだったね。
つまり、n=1のK殻は１個（1s：1個）、n=2のL殻では４個（2s：1個、2p：3個）、n=3のM殻では９個（3s：1個、3p：3個、3d：5個）のエネルギーはそれぞれすべて同じ値となるんだね。
このように異なる固有状態が同じ同じエネルギーとなることは「縮退」と呼ばれるんだったね。縮退は対称性が高いほど生じるよ。

水素原子核の周りを運動する電子に外場を加えるとどうなるの？

水素原子核の周りを運動する電子に外から何かの力を加えるとハミルトニアンはもとのハミルトニアンを$\hat{H}_0$と表して

\begin{align}
\hat{H} = \hat{H}_0 + V
\end{align}

という形に変化するよ。$V$は外から加えられた力によるポテンシャルエネルギーだよ。
外からの力は外場と呼ばれるよ。外場が加えられると $\varphi_{nlm}$ はハミルトニアンの固有状態ではなくなっちゃうんだよね。
そこで新しい固有状態を$\psi$として、新しい固有方程式

\begin{align}
\hat{H} \psi = E \psi
\end{align}

を解き直す必要があるわけだね。

外場が加えられたときの固有方程式の解き方

外場がない場合の固有関数$\varphi_{nlm}$は正規直交完全系をなすので、外場が加えられたときの固有状態$\psi$は$\varphi_{nlm}$で重ね合わせで表すことができるので、

\begin{align}
\psi = \sum_{n, l, m} a_{nlm} \varphi_{nlm}
\end{align}

と表わすことができるよ。$a_{nlm}$は展開係数だね。
展開係数が決定できれば固有方程式を解いたことになるので、展開係数に関する方程式を導く必要があるよ。
まずは代入して、

\begin{align}
\sum_{n, l, m} a_{nlm} \left[ E_n + V \right] \varphi_{nlm} = E \sum_{n, l, m} a_{nlm} \varphi_{nlm}
\end{align}

そして、両辺に$\varphi_{nlm}$の複素共役$\varphi_{n’l’m’}^*$を掛けて全空間で積分すると

\begin{align}
E_{n’} a_{n’l’m’} + \sum_{n, l, m}a_{nlm} V^{n’l’m’}_{nlm} = E a_{n’l’m’}
\end{align}

となって、$a_{n’l’m’}$に関する連立方程式が導かれるんだね。$V^{n’l’m’}_{nlm}$は式を簡略化するために改めて定義した

\begin{align}
V^{n’l’m’}_{nlm} \equiv \int_0^\infty\!\!\! r^2 dr \int_0^\pi \!\!\! \sin\theta d\theta \int_0^{2\pi} \!\!\! d\phi \left[\varphi_{n’l’m’}^* V \varphi_{nlm} \right]
\end{align}

だよ。連立方程式は行列で表すとわかりやすくなるので、エネルギーの小さい順に固有関数の係数を並べると次のようになるよ。

\begin{align}
\left(\matrix{ E_1 +V_{100}^{100} & V_{200}^{100}& V_{21-1}^{100} & V_{210}^{100} & V_{211}^{100} & \cdots \cr
V_{100}^{200} & E_2 + V_{200}^{200}& V_{21-1}^{200} & V_{210}^{200} &V_{211}^{200} &\cdots \cr
V_{100}^{21-1} & V_{200}^{21-1} & E_2 + V_{21-1}^{21-1} & V_{210}^{21-1}& V_{211}^{21-1}& \cdots \cr
V_{100}^{210} & V_{200}^{210} & V_{21-1}^{210} & E_2 + V_{210}^{210}& V_{211}^{210}& \cdots \cr
V_{100}^{211} & V_{200}^{211} & V_{21-1}^{211} & V_{210}^{211}& E_2 + V_{211}^{211}& \cdots \cr
\vdots & \vdots & \vdots & \vdots & \vdots & \ddots } \right) \left(\matrix{ a_{100} \cr a_{200} \cr a_{21-1} \cr a_{210} \cr a_{211} \cr \vdots }\right) = E \left(\matrix{ a_{100} \cr a_{200} \cr a_{21-1} \cr a_{210} \cr a_{211} \cr \vdots }\right)
\end{align}

まさに行列表した固有値方程式の形になっているのがわかるね。
これで固有値と固有ベクトルを計算すると、固有値はそのまま外場が加えられた場合のエネルギー、固有ベクトルがそのまま展開係数の値そのものになるね。
次回は、外場として電場を加えたときの様子をシミュレーションします！