タグ: 電磁波

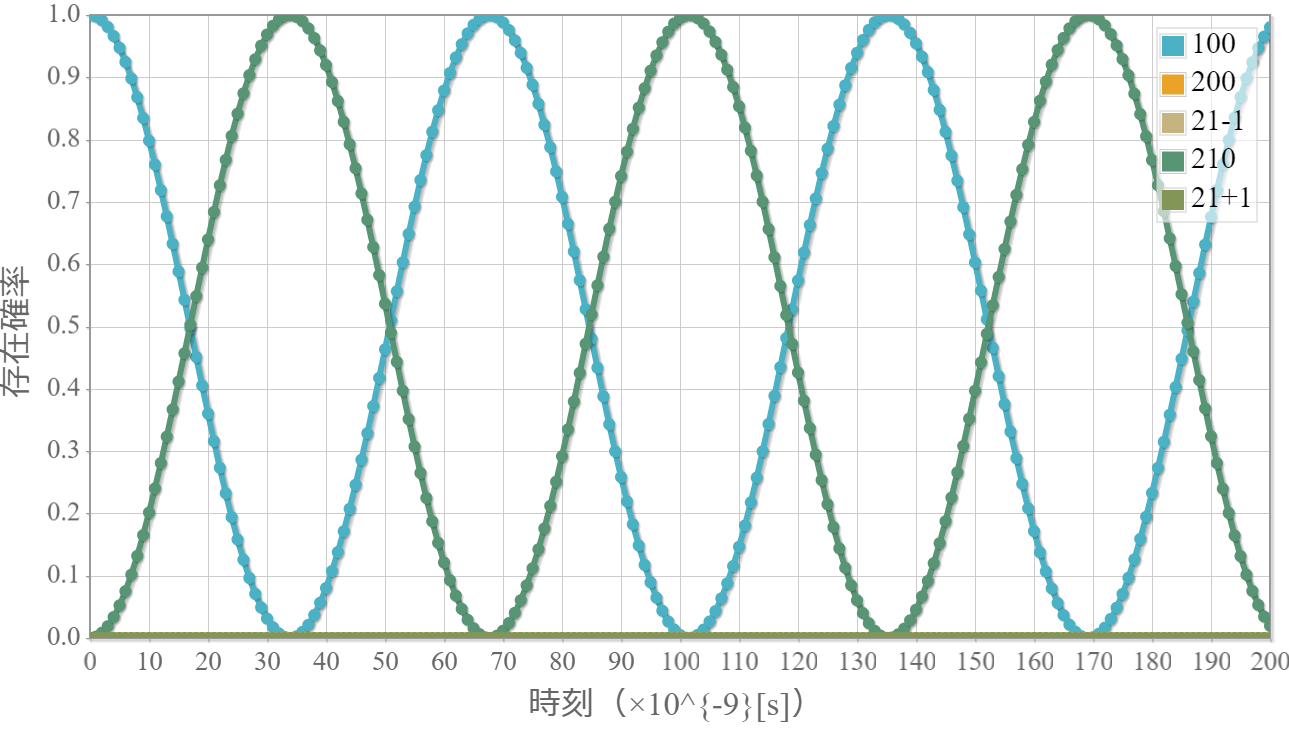
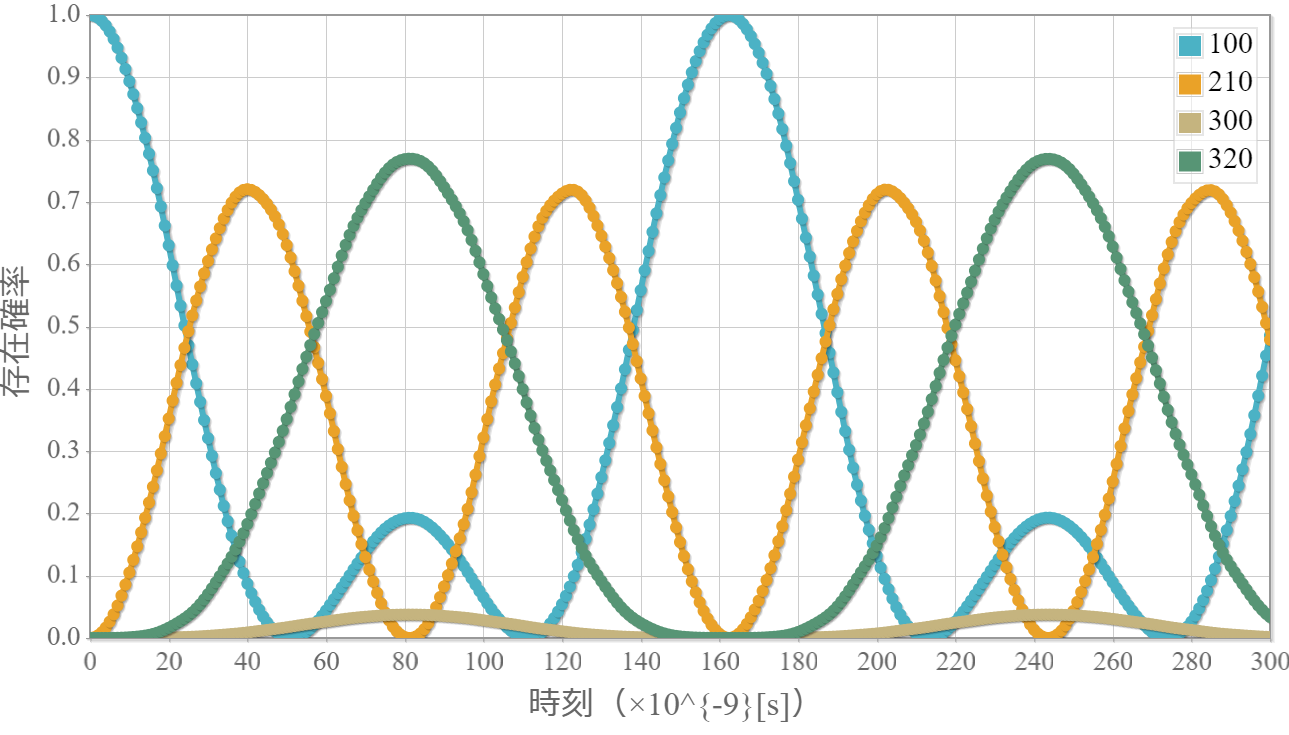
直線偏光の古典電磁波を水素原子に束縛された電子のハミルトニアンは以前示したね。今度は、円偏光の場合を導出するよ。偏光を考慮したベクトルポテンシャルは

\begin{align}
\boldsymbol{A} = \left\{ \matrix{ 0 \cr A_{y0} \cos(kx-\omega t + \phi_y) \cr A_{z0} \cos(kx-\omega t+ \phi_z)} \right.
\end{align}

と与えると、電場と磁場は次のようになるね。

\begin{align}
\boldsymbol{E} = -\frac{\partial \boldsymbol{A}}{\partial t} =\left\{ \matrix{ 0 \cr -\omega A_{y0} \sin(kx-\omega t + \phi_y) \cr -\omega A_{z0} \sin(kx-\omega t+ \phi_z)} \right.
\end{align}
\begin{align}
\boldsymbol{B} = \nabla \times \boldsymbol{A} =\left\{ \matrix{ 0 \cr k A_{z0} \sin(kx-\omega t + \phi_z) \cr -k A_{y0} \sin(kx-\omega t+ \phi_y)} \right.
\end{align}

これを電磁場中の電子のハミルトニアン

\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \boldsymbol{p} + \frac{e}{m_e} \hat{\boldsymbol{S}}\cdot \boldsymbol{B} + \frac{e^2 \boldsymbol{A}^2}{2m_e}
\end{align}

に代入すると完成だね。

電磁波による状態遷移の数値計算

時間依存性を計算するために、ハミルトニアンの時間依存部分 $\hat{V}(t)$ の空間積分の項を見てみよう。

\begin{align}
\int \varphi_{n’l’m’\sigma’}^* \hat{V}(t)\varphi_{nlm\sigma} dV &\ = \int \varphi_{n’l’m’\sigma’}^* \left[
-i\frac{e}{\hbar} [\hat{H}_0,\boldsymbol{r} ]\cdot\boldsymbol{A} + \frac{e }{m_e} \hat{\boldsymbol{S}}\cdot\boldsymbol{B} + \frac{e^2 \boldsymbol{A}^2}{2m_e} \right] \varphi_{nlm\sigma} dV \\
&\ = \int \varphi_{n’l’m’\sigma’}^* \left[
-ie \frac{ E_{n’} – E_n }{\hbar}\,\boldsymbol{r}\cdot\boldsymbol{A} + \frac{e }{m_e} \hat{\boldsymbol{S}}\cdot\boldsymbol{B} + \frac{e^2 \boldsymbol{A}^2}{2m_e} \right] \varphi_{nlm\sigma} dV
\end{align}

スピンと２次の項を無視して、さらに長波長近似（電磁波の波長が原子サイズより十分に大きいとする近似）を行うと、

\begin{align}
\int \varphi_{n’l’m’}^* \hat{V}(t)\varphi_{nlm} dV &\ \simeq -ie \int \varphi_{n’l’m’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\,(yA_y +zA_z) \right] \varphi_{nlm} dV \\
&\ = \frac{-ie}{2}\,\frac{ E_{n’} – E_n }{\hbar} \left[A_{y0}\cos(\omega t – \phi_y) \int \varphi_{n’l’m’}^* y \varphi_{nlm} dV + A_{z0}\cos(\omega t – \phi_z) \int \varphi_{n’l’m’}^* z \varphi_{nlm} dV\right]
\end{align}

となるね。入射波を円偏光とするには、 $A_{y0} = A_{z0} = A_{0}$ かつ $\phi_y = 0 , \phi_z = \pm \pi/2 $ とすれば良いので、これを代入すると、

\begin{align}
\int \varphi_{n’l’m’}^* \hat{V}(t)\varphi_{nlm} dV &\ \simeq -ie \int \varphi_{n’l’m’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\,(yA_y +zA_z) \right] \varphi_{nlm} dV \\
&\ = \frac{-ieA_0}{2}\,\frac{ E_{n’} – E_n }{\hbar} \left[\cos(\omega t) \int \varphi_{n’l’m’}^* y \varphi_{nlm} dV \pm \sin(\omega t) \int \varphi_{n’l’m’}^* z \varphi_{nlm} dV\right]
\end{align}

となるね。このハミルトニアンを元に次回は水素原子の基底状態にいる電子に円偏光電磁波を与えてみるよ。

以前解説したハミルトニアンを用いて、水素原子の基底状態の電子に電磁波（古典・直線偏光）を入射したの様子をシミュレーションしたよ。結果を示すね。

角振動数 $\omega_{12} = (E_2-E_1)/\hbar$ の電磁波を入射

次のグラフは、基底状態と第１励起状態のエネルギー準位の差に対応する電磁波を入射した結果だよ。$ \varphi_{100} $ と $ \varphi_{210} $ の間でラビ振動している様子が分かるね。

角振動数 $\omega_{12} = (E_2-E_1)/\hbar$ と $\omega_{23} = (E_3-E_2)/\hbar$の電磁波を入射

次のグラフは、基底状態と第１励起状態のエネルギー準位の差に対応する電磁波と、第１励起状態と第２励起状態ののエネルギー準位の差に対応する電磁波を同時に入射した結果だよ。$ \varphi_{100} $ と $ \varphi_{210} $ に加えて、$ \varphi_{100} $ から直接遷移することができない $ \varphi_{300} $ と $ \varphi_{320} $ にも励起しているね。このように、直接遷移が許されない状態が加わっても、存在確率が周期的に振動するのはちょっと意外だね。

次回は、円偏光の電磁波を入射するよ。

任意の電磁場中を運動する電子のハミルトニアンは「静磁場が加わる場合のハミルトニアンを復習しよう！」で示したとおりだね。ベクトルポテンシャルを $\boldsymbol{A}$、スカラーポテンシャルを $\phi$ とした場合、

\begin{align}
\hat{H} = \frac{1}{2m_e} (\hat{\boldsymbol{p}} + e \boldsymbol{A})^2 -e \phi
\end{align}

となるね。水素原子に束縛された電子を考えると、クーロンゲージを採用して

\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \boldsymbol{p} + \frac{e^2 \boldsymbol{A}^2}{2m_e}
\end{align}

となるね。$\hat{H}_0$ は外場が無い場合の水素原子に束縛された電子のハミルトニアン

\begin{align}
\hat{H}_0 = \frac{\hat{\boldsymbol{p}}^2}{2m_e} – \frac{e^2}{ 4\pi\epsilon_0} \, \frac{1}{r}
\end{align}

だよ。電磁波の場合には、このベクトルポテンシャル $\boldsymbol{A}(t)$ が時間に依存するんだね。さらに、スピンも考慮するならば、スピンのゼーマン項を加えて

\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \boldsymbol{p} + \frac{e}{m_e} \hat{\boldsymbol{S}}\cdot \boldsymbol{B} + \frac{e^2 \boldsymbol{A}^2}{2m_e}
\end{align}

だね。今回、電磁波の進行方向をx軸として、磁場成分をy軸、電場成分をz軸となるように、ベクトルポテンシャルを

\begin{align}
\boldsymbol{A} = \left(0, 0, A_0 \cos(kx-\omega t) \right)
\end{align}

と与えると、電場と磁場は次のようになるね。

\begin{align}
\boldsymbol{E} &\ = -\frac{\partial \boldsymbol{A}}{\partial t} =\left(0, 0, – \omega A_0 \sin(kx-\omega t) \right)\\
\boldsymbol{B} &\ = \nabla \times \boldsymbol{A} =\left(0, k A_0 \sin(kx-\omega t), 0 \right)
\end{align}

電磁波による状態遷移の数値計算

電子の状態遷移を議論するには、時間に依存したシュレディンガー方程式

\begin{align}
i\hbar\frac{\partial}{\partial t} \psi(\boldsymbol{r}, t) = \hat{H} \psi(\boldsymbol{r}, t)
\end{align}

を解けばいいんだね。まずは波動関数 $\psi(\boldsymbol{r}, t) $ を外場無し固有状態で

\begin{align}
\psi(\boldsymbol{r}, t) = \sum\limits_{n, l, m, s_z} a_{nlms_z}(t)\, \varphi_{nlms_z}
\end{align}

のように展開して、展開係数が時間に依存すると考えることができるね。次に、$\hat{H} = \hat{H}_0 + \hat{V}(t)$ とおいてこれをシュレディンガー方程式に代入すると

\begin{align}
\sum\limits_{n, l, m, s_z}i\hbar\frac{d a_{nlms_z}(t)}{d t} \, \varphi_{nlms_z} = \sum\limits_{n, l, m, s_z}\left[E_n + \hat{V}(t)\right] a_{nlms_z}(t)\, \varphi_{nlms_z}
\end{align}

となるね。両辺に $\varphi_{n’l’m’s_z’}^*$ を掛けて全空間で積分すると展開係数に関する連立常微分方程式が得られるね。

\begin{align}
i\hbar\frac{d a_{n’l’m’s_z’}(t)}{d t} = E_{n’}a_{n’l’m’s_z’}(t) + \sum\limits_{n, l, m, s_z} a_{nlms_z}(t) \int \varphi_{n’l’m’s_z’}^* \hat{V}(t)\varphi_{nlms_z} dV
\end{align}

この $\hat{V}(t)$ に電磁波との相互作用を与えるわけだね。$\hat{\boldsymbol{p}}/m_e = -i [\hat{H}_0,\boldsymbol{r} ]/\hbar$ を考慮して、$\hat{V}(t)$ の空間積分の項を見てみよう。

\begin{align}
\int \varphi_{n’l’m’s_z’}^* \hat{V}(t)\varphi_{nlms_z} dV &\ = \int \varphi_{n’l’m’s_z’}^* \left[
-i\frac{e}{\hbar} [\hat{H}_0,\boldsymbol{r} ]\cdot\boldsymbol{A} + \frac{e }{m_e} \hat{S}_yB_y + \frac{e^2 A_0^2}{2m_e}\, \cos^2(kx-\omega t) \right] \varphi_{nlms_z} dV \\
&\ = \int \varphi_{n’l’m’s_z’}^* \left[
-ie \frac{ E_{n’} – E_n }{\hbar}\, z A_0 \cos(kx-\omega t) + \frac{ek\hbar A_0 s_z}{m_e} \,\sin(kx-\omega t) + \frac{e^2 A_0^2}{2m_e}\, \cos^2(kx-\omega t) \right] \varphi_{nlms_z} dV \\
&\ = -\frac{i A_0e}{2} e^{-i\omega t}\int \varphi_{n’l’m’s_z’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z + \frac{k\hbar s_z}{m_e} \right] e^{ikx} \varphi_{nlms_z} dV\\
&\ \ \ \ \ -\frac{i A_0e}{2} e^{i\omega t}\int \varphi_{n’l’m’s_z’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z – \frac{ k\hbar s_z}{m_e} \right] e^{-ikx} \varphi_{nlms_z} dV\\
&\ \ \ \ \ + \frac{e^2 A_0^2}{8m_e} \left[ 1 + e^{-2i\omega t} \int \varphi_{n’l’m’s_z’}^* e^{2ikx} \varphi_{nlms_z} dV + e^{2i\omega t} \int \varphi_{n’l’m’s_z’}^* e^{-2ikx} \varphi_{nlms_z} dV \right]
\end{align}

最後の変形は時間依存部分を積分の外に出すために、

\begin{align}
\cos(kx-\omega t) &\ = \frac{1}{2} \left[ e^{ikx-i\omega t} + e^{-ikx+i\omega t} \right]\\
\sin(kx-\omega t) &\ = \frac{1}{2i} \left[ e^{ikx-i\omega t} – e^{-ikx+i\omega t} \right]\\
\end{align}

と変形しているよ。ちょっと複雑になったけれども、時間依存部分はすべて積分の外に出たので、時間ステップごとに積分を実行しなくて済むね。あとは、ルンゲ・クッタ法などの常微分方程式を解く計算アルゴリズムで、この連立常微分方程式が得られるね。ちなみに、$\hat{\boldsymbol{p}}\cdot\boldsymbol{A}$ は電子の軌道運動による電磁波の吸収と放出を、$\hat{\boldsymbol{s}}\cdot\boldsymbol{B}$ は電子のスピンによる電磁波の吸収と放出を表すよ。また、$\boldsymbol{A}^2$ は電磁場の量子化後に分かるけれども、光子の２個吸収、２個放出、光子の散乱に寄与するよ。

スピンと２次の項を無視する場合

先のポテンシャル積分項にて、スピンと２次の効果を無視すると

\begin{align}
\int \varphi_{n’l’m’}^* \hat{V}(t)\varphi_{nlm} dV = -\frac{i A_0e}{2} \left[e^{-i\omega t}\int \varphi_{n’l’m’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z \right] e^{ikx} \varphi_{nlm} dV + e^{i\omega t}\int \varphi_{n’l’m’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z \right] e^{-ikx} \varphi_{nlm} dV \right]
\end{align}

となるね。さらに、原子サイズに対して、波の波長が十分に大きい場合、$ e^{ikx} \simeq 1 $、$ e^{-ikx} \simeq 1$ が十分成り立つね（光子のエネルギー $10[{\rm eV}]$ の波長が約 $100 [{\rm nm}]$ なので十分だね）。積分に関係ない部分をすべて外に出すと

\begin{align}
\int \varphi_{n’l’m’}^* \hat{V}(t)\varphi_{nlm} dV = -i A_0e \frac{ E_{n’} – E_n }{\hbar} \cos(\omega t) \int \varphi_{n’l’m’}^* z \varphi_{nlm} dV
\end{align}

となって、ポテンシャル積分項は、係数を除いて、実質的に以前解説した電気双極子の行列要素と一致するね。このハミルトニアンを元に、次回は水素原子の基底状態にいる電子に電磁波を与えてみるよ。