投稿者: simu-kun

「ヘリウム原子のエネルギー固有状態の計算方法」に基づいて、ヘリウム原子のエネルギー準位と固有関数の空間分布を計算したよ。「ヘリウム原子の基底状態の計算結果」で示したとおり、計算結果はよく知られた精密な実験結果とかなり一致しているよ。

ヘリウム原子のエネルギー準位

次の図は、パラ（対称関数・スピン１重項）とオルト（反対称関数・スピン３重項）の主量子数 $n=1,2,3$
のエネルギー準位だよ。オルトのほうがパラよりも若干小さな値となるね。これは交換相互作用の結果だね。イオン化エネルギーは、電子２個の基底状態から電子１個を引き離すために必要なエネルギーで、「基底状態エネルギー（$-79.18[{\rm
eV}]$）」から「電子が１個のみのヘリウム原子の基底状態エネルギー（ $-54.4[{\rm eV}]$ ）」で計算できるよ。

ヘリウム原子の固有状態の空間分布

今回も独立電子近似の場合と同様、粒子の１つが
$\varphi_{100}(\boldsymbol{r})|$の最も確率の高い原点（ $\boldsymbol{r}_1=0$ あるいは $\boldsymbol{r}_2=0$
）に存在するとして、他方の粒子の空間確率密度を描画するよ。最初の表がパラヘリウム（対称関数・スピン1重項）、次の表がオルトヘリウム（反対称関数・スピン3重項）だよ。

（※実際の表はこちらのページを見てね！）

ちなみにヘリウム原子の場合、直交関数系は $(1,0,0)$ を必ず含むよ。なぜならば、$(1,0,0)$ から次に低い $(2,0,0)$ とした場合の固有エネルギーは約 $-20[{\rm eV}]$
で、イオン化エネルギーよりも高くなるために実質的には先に電離してしまうね。

水素原子の電子に直線偏光の電磁波（古典）を入射したときの状態遷移は以前解説したね。今回は、入射した電磁波の振動数を高めることで生じる「光電効果」（束縛状態の電子が外場によって非束縛状態へ遷移する効果）をシミュレーションするのに必要な表式を導出するよ。スピンと外場の２次の項を無視したハミルトニアンは、

\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}} = -\frac{\hbar^2}{2m_e}\nabla^2 + V(r) + \frac{e}{im_e} \,\boldsymbol{A}\cdot\nabla
\end{align}

となるね。このハミルトニアンを用いたシュレディンガー方程式

\begin{align}
i\hbar\frac{\partial}{\partial t} \psi(\boldsymbol{r}, t) = \hat{H} \psi(\boldsymbol{r}, t)
\end{align}

だね。ここから出発するよ。今回は、水素原子核に束縛された状態からとき放たれた状態も考慮するため、波動関数は波数空間で展開した

\begin{align}
\psi(\boldsymbol{r}, t) = \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z} a_{n_xn_yn_z}(t)\, e^{i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}

で表すよ。ただし、$ \boldsymbol{k} = \frac{2\pi}{L}(n_x, n_y, n_z) $ で、$L$ は空間サイズで $V =L^3$、 $n_x, n_y, n_z$ は整数だよ。これをシュレディンガー方程式に代入して、両辺に $\frac{1}{\sqrt{V}}e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}}$ を掛けて、全空間で積分すると

\begin{align}
i\hbar\frac{d a_{n_x’n_y’n_z’}(t)}{d t} = \left[ \frac{\hbar^2k’^2}{2m_e} + \frac{e}{m_e} \,\boldsymbol{A}\cdot \boldsymbol{k}’ \right] a_{n_x’n_y’n_z’}(t) + \frac{1}{V}\sum\limits_{n_x, n_y, n_z} \left[ \int e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}} V(r) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} dV \right] a_{n_xn_yn_z}(t)
\end{align}

となるね。さらにポテンシャル項もついでに

\begin{align}
V(r) = \frac{1}{\sqrt{V}}\sum\limits_{n”_x, n”_y, n”_z} v_{n”_xn”_yn”_z}\, e^{i\boldsymbol{k}”\cdot\boldsymbol{r}}
\end{align}

と展開して代入すると、空間積分を実行することができて、次のような形になるね。

\begin{align}
i\hbar\frac{d a_{n_x’n_y’n_z’}(t)}{d t} = \left[ \frac{\hbar^2k’^2}{2m_e} + \frac{e}{im_e} \,\boldsymbol{A}\cdot \boldsymbol{k}’ \right] a_{n_x’n_y’n_z’}(t) + \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z}\,v_{n_x’-n_x,n_y’-n_y,n_z’-n_z} a_{n_xn_yn_z}(t)
\end{align}

さらに、クーロンポテンシャル $ V(r) = -e^2/4\pi\epsilon r$のように $1/r$ の場合には、展開係数 $ v_{n”_xn”_yn”_z} $ は解析的に導出することができて、

\begin{align}
v_{n”_xn”_yn”_z} = \frac{1}{\sqrt{V}} \int V(r)e^{-i\boldsymbol{k}”\cdot\boldsymbol{r}} dV = -\frac{e^2}{4\pi\epsilon_0} \, \frac{1}{k”^2}
\end{align}

で与えられるので、最終的には

\begin{align}
i\hbar\frac{d a_{n_x’n_y’n_z’}(t)}{d t} = \left[ \frac{\hbar^2k’^2}{2m_e} + \frac{e}{im_e} \,\boldsymbol{A}\cdot \boldsymbol{k}’ \right] a_{n_x’n_y’n_z’}(t) -\frac{e^2}{4\pi\epsilon_0}\, \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z}\,\frac{1}{k_{n_x’-n_x,n_y’-n_y,n_z’-n_z}^2 }a_{n_xn_yn_z}(t)
\end{align}

となるね。これで、$a_{n_xn_yn_z}$ に関する連立常微分方程式になるね。あとは、外場を与えるベクトルポテンシャル $\boldsymbol{A}$ を計算対象の系に合わせて設定して、ルンゲ・クッタ法を用いて時間発展を計算することができるね。ちなみに、$a_{n_xn_yn_z}$ の初期状態は、

\begin{align}
a_{n_xn_yn_z}(0) = \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z} \psi(\boldsymbol{r}, 0) \, e^{-i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}

で計算することができるので、例えば、$\psi(\boldsymbol{r}, 0) = \varphi_{100}$ と与えることで、初期状態を基底状態とした場合の計算を行うことができるよ。次回は結果を示すよ。

あとで、電磁波（古典）による「光電効果」（束縛状態の電子が外場によって非束縛状態へ遷移する効果）をシミュレーションしたいので、その準備として、水素原子に束縛された固有状態のフーリエ変換を数値的に調べておくよ。$ \boldsymbol{k} = \frac{2\pi}{L}(n_x, n_y, n_z) $ で、$L$ は空間サイズで $V =L^3$、 $n_x, n_y, n_z$ は整数として、固有状態の波数成分 $\varphi_{nlm}( \boldsymbol{k} )$ は、

\begin{align}
\varphi_{nlm}( \boldsymbol{k} ) = \frac{1}{\sqrt{V}} \int \varphi_{nlm}( \boldsymbol{r} ) e^{-i \boldsymbol{k} \cdot \boldsymbol{r} }dV
\end{align}

で表すことができるね。とりあえず、基底状態 $\varphi_{100}( \boldsymbol{k} ) $ の波数空間分布を示すよ（ $\varphi_{100}( \boldsymbol{k} ) $ の $kx-ky$ 平面上の値を、大きさは不透明度、位相は色で表しているよ）。

独立電子近似の場合、ヘリウム原子の２つの電子の波動関数は、個々の水素様原子（ $Z=2$ ）の波動関数の積を用いて、空間対称（スピン３重項／パラ）あるいは空間反対称（スピン１重項／オルト）の２つの状態をとるよ。具体的な波動関数の表式はそれぞれ

\begin{align}
\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) + \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) – \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\end{align}

と表されるね。この波動関数は各粒子ごとに３次元で合計で６次元の関数なので、これを描画するには工夫が必要になるよ。１番基本的な考え方は、空間位置 $ \boldsymbol{r} $ に粒子１あるいは粒子２が存在する空間確率密度を

\begin{align}
\rho( \boldsymbol{r} ) = \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}) |^2 dV_1 + \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, \boldsymbol{r}_2) |^2 dV_2
\end{align}

と定義することで、空間分布を計算することができるね。ただし、これを先の $\chi^{(S)}$ と $\chi^{(A)}$ に適用すると、

\begin{align}
\rho^{(S)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2\\
\rho^{(A)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2
\end{align}

となって、それぞれの粒子の空間分布の和となるね。ヘリウム原子の低エネルギーの状態は、粒子の片方は必ず $(n,l,m)=(1,0,0)$ に存在するので、先の空間確率密度を数値的に計算すると、他方の粒子がどの準位に存在したとしても、 $|\varphi_{100}(\boldsymbol{r})|^2 >> |\varphi_{nlm}(\boldsymbol{r})|^2 $ となって、実質的に $|\varphi_{100}(\boldsymbol{r})|^2$ となってしまうね。これは、２つの粒子が存在する確率が $|\varphi_{100}(\boldsymbol{r})|^2$ で表される領域に集中していることを意味しているよ。

そこで今回は、粒子の１つが $\varphi_{100}(\boldsymbol{r})|$の最も確率の高い原点（ $\boldsymbol{r}_1=0$ あるいは $\boldsymbol{r}_2=0$ ）に存在するとして、他方の粒子の空間確率密度

\begin{align}
\rho^{(S)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, 0)|^2 \\
\rho^{(A)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r},0)|^2
\end{align}

を定義して、空間分布を描画したよ。ちなみに両者とも第１項目と第２項目の値は同じ値となるよ。

（※実際の表はこちらのページを見てね！）

上記の結果は単に $|\varphi_{nlm}(\boldsymbol{r})|^2$ を計算した結果に似ているけれども異なるよ。空間対称関数と空間反対称関数では、概ね同じだけれども顕著に異なるのが、２個目の粒子の状態が $(n,l,m) =(2,0,0)$ や $(n,l,m) =(3,0,0)$ で、原点を中心に存在する場合だね。これは、空間対称関数の場合には、同じ領域に居ようとするけれども、空間反対称関数の場合には、互いに避けようとする結果だね。次回は、電子間の相互作用を加味した波動関数を描画するよ。

スピン１／２の粒子２個が存在する場合、それぞれのスピンの値によって、波動関数の空間部分は「対称」あるいは「反対称」となることが知られているね。今回は、最も簡単な１次元自由空間中で２個の粒子が平面波で表される場合の空間分布を復習するよ。波動関数の空間部分の対称関数と反対称関数はそれぞれ

\begin{align}
\psi^{(S)}(x_1, x_2, t) &\ = \frac{1}{\sqrt{2}} \left[ e^{i k_1\cdot x_1 +i k_2\cdot x_2} + e^{i k_1\cdot x_2 +i k_2\cdot x_1}\right]e^{-i\omega t} \\
\psi^{(A)}(x_1, x_2, t) &\ =\frac{1}{\sqrt{2}} \left[ e^{i k_1\cdot x_1 +i k_2\cdot x_2}- e^{i k_1\cdot x_2 +i k_2\cdot x_1}\right]e^{-i\omega t}\\
\end{align}

となるね。ただし、

\begin{align}
E_1 = \frac{\hbar^2 k_1^2}{2m_e} \ , \ E_2 = \frac{\hbar^2 k_2^2}{2m_e} \ , \ E = E_1 + E_2 \ , \ \omega = \frac{E}{\hbar}
\end{align}

の関係があるよ。この波動関数は、粒子１と粒子２のそれぞれの位置 $x_1$ と $x_2$ を与えたときの振幅を与えるので、１次元上で波動関数の様子を可視化するには工夫が必要になるね。今回は、粒子１の位置をゼロ、すなわち $x_1 =0$ として、横軸を粒子２の位置 $x_2$、縦軸を波動関数の実部、虚部、絶対値の２乗の値とするね。なお、波動関数の絶対値の２乗

\begin{align}
|\psi^{(S)}(x_1, x_2, t)|^2 &\ = 1 + \cos\left[ (k_1 – k_2)(x_1 – x_2) \right]\\
|\psi^{(A)}(x_1, x_2, t)|^2 &\ = 1 – \cos\left[ (k_1 – k_2)(x_1 – x_2) \right]\\
\end{align}

は、各点における粒子の存在確率（今回、規格化が不十分だったので最大値が２になってしまったよ）を表すよ。２粒子の場合には相対位置のみ依存しているね。

計算結果

$E_1=1.0[{\rm eV}]$（右向き）と $E_2=1.5[{\rm eV}]$（右向き）

まずは、同じ方向へ進む２粒子の場合の計算結果を示すよ。粒子１の位置を $x_1 =0$ としているよ。対称関数の場合には粒子２はゼロ近傍にいる確率が高い反面、反対称波動関数の粒子２はゼロ近傍が一番低くなっているね。

対称関数

反対称関数

$E_1=1.0[{\rm eV}]$（右向き）と $E_2=1.5[{\rm eV}]$（左向き）

次は、反対方向へ進む２粒子の場合の計算結果を示すよ。粒子１の位置を $x_1 =0$ としているよ。異なるエネルギー（波数）の干渉なのに、粒子２の存在確率が時間に依存しないのは、ちょっと不思議だけれども、先に示した絶対値の２乗の表式は時間に依存しないから当たり前だよね。あと、絶対値の２乗の波数が大きくなったね。これは、波数 $k_1$ と $k_2$ の差が存在確率の波数に対応していることで理解できるね。

対称関数

反対称関数

$E_1=1.0[{\rm eV}]$（右向き）と $E_2=1.0[{\rm eV}]$（左向き）

最後に、同じエネルギーの２粒子が反対方向へ進む場合の計算結果を示すよ。粒子１の位置を $x_1 =0$ としているよ。

対称関数

反対称関数

粒子が１個の場合は単純な平面波だけれども、２個になった途端に複雑さが増していくね。

前回、ヘリウム原子の電子状態の計算方法を示したね。その計算結果のうち、今回は基底状態を示すよ。ヘリウムの基底状態は２つの電子のスピンが上向きと下向きの反対称で、波動関数の空間部分は対称関数となるね。そのため、正規直交完全系をなす対称関数で展開して

\begin{align}
\psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \sum_{\alpha,\alpha’} s_{\alpha\alpha’}\chi^{(S)}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

エネルギー固有状態を計算したよ。その結果、基底状態のエネルギー固有値が $ E_{\rm calculate} = -79.18 [{\rm eV}]$ となって、よく知られた実験値 $E_{\rm experiment } = -78.98 [{\rm eV}] $ と比較してわずか $0.2\%$ のずれの結果を得ることができたよ。

計算結果：ヘリウム原子の基底状態

基底状態の固有関数は、水素様原子 $(1s)^2$ の固有関数 $\chi^{(S)}_{1s1s}$ と $(1s)(2s)$ の固有関数 $\chi^{(S)}_{1s2s}$の２つの項の重ね合わせ

\begin{align}
\psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) = s_{1s1s}\chi^{(S)}_{1s1s}(\boldsymbol{r}_1, \boldsymbol{r}_2) + s_{1s2s}\chi^{(S)}_{1s2s}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

で、$ s_{1s1s} \simeq 0.922 \ , \ s_{1s2s} \simeq -0.384 $ の場合に

\begin{align}
E_{\rm calculate} =\int \!\!\! \int \psi^{(S)}(\boldsymbol{r}_1,\boldsymbol{r}_2)^* \hat{H} \psi^{(S)}(\boldsymbol{r}_1,\boldsymbol{r}_2) dV_1dV_2 \simeq -79.18 [{\rm eV}]
\end{align}

となるよ。この結果は、非摂動１電子近似の $ -108.8 [{\rm eV}] $、１次の摂動近似の $-74.8 [{\rm eV}]$、１電子近似に変分法を適用した $-77.5[{\rm eV}]$ と比較して、実験結果を非常によく一致しているね。つまり、ヘリウム原子の基底状態は $ |s_{1s1s}|^2 \simeq 0.850 \ , \ |s_{1s2s}|^2 \simeq 0.147 $ の割合で水素様原子固有状態 $\chi^{(S)}_{1s1s}$ と $\chi^{(S)}_{1s2s}$ の状態が重ね合わさった状態であることがわかったよ。ちなみに $\chi^{(S)}_{1s1s}$ と $\chi^{(S)}_{1s2s}$ は次のとおりだよ。

\begin{align}
\chi^{(S)}_{1s1s}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \varphi_{100}(\boldsymbol{r}_1)\varphi_{100}(\boldsymbol{r}_2)\\
\chi^{(S)}_{1s2s}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}}\left[\varphi_{100}(\boldsymbol{r}_1)\varphi_{200}(\boldsymbol{r}_2)+\varphi_{100}(\boldsymbol{r}_2)\varphi_{200}(\boldsymbol{r}_1)\right]
\end{align}

ヘリウム原子の電子の波動関数は２変数関数なので、３次元空間で波動関数を表すことが単純にはできないね。次回、波動関数の可視化を工夫してみよう。また、ヘリウム原子の電子のエネルギー準位を整理してまとめるよ。

前回、ヘリウム原子に存在する２つの電子の波動関数について解説しました。この表式は、原子核との相互作用や粒子同士の相互作用が無い場合にも対応することができるので、自由空間中の２つの粒子の運動を調べてみるよ。自由空間の固有状態は平面波 $\exp( i \boldsymbol{k}\cdot \boldsymbol{r} )$ なので、これを基底関数系として空間対称・空間反対称の波動関数を次のように表すよ。

\begin{align}
\psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2, t) &\ =\sum_{n_1,n_2} c_{n_1,n_2} \chi^{(S)}_{n_1,n_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)e^{-i\omega t} =\sum_{n_1,n_2} c_{n_1,n_2} \left( e^{i \boldsymbol{k}_{n_1}\cdot \boldsymbol{r}_1 +i \boldsymbol{k}_{n_2}\cdot \boldsymbol{r}_2} + e^{i \boldsymbol{k}_{n_1}\cdot \boldsymbol{r}_2 +i \boldsymbol{k}_{n_2}\cdot \boldsymbol{r}_1}\right)e^{-i\omega t} \\
\psi^{(A)}(\boldsymbol{r}_1, \boldsymbol{r}_2, t) &\ =\sum_{n_1,n_2} c_{n_1,n_2} \chi^{(A)}_{n_1,n_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)e^{-i\omega t} = \sum_{n_1,n_2}
c_{n_1,n_2} \left( e^{i \boldsymbol{k}_{n_1}\cdot \boldsymbol{r}_1 +i \boldsymbol{k}_{n_2}\cdot \boldsymbol{r}_2}
– e^{i \boldsymbol{k}_{n_1}\cdot \boldsymbol{r}_2 +i \boldsymbol{k}_{n_2}\cdot \boldsymbol{r}_1}\right)e^{-i\omega t}\\
\end{align}

空間対称・空間反対称の波動関数は、それぞれ次のシュレーディンガー方程式を満たすよ。

\begin{align}
i\hbar \frac{\partial }{ \partial t} \psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2, t) &\ = \hat{H} \psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2, t) \\
i\hbar \frac{\partial }{ \partial t} \psi^{(A)}(\boldsymbol{r}_1, \boldsymbol{r}_2, t) &\ = \hat{H}
\psi^{(A)}(\boldsymbol{r}_1, \boldsymbol{r}_2, t)
\end{align}

\begin{align}
(\hat{H}_1+\hat{H}_2) \chi^{(S)}_{n_1,n_2}(\boldsymbol{r}_1, \boldsymbol{r}_2) = (E_{n_1}+E_{n_2}) \chi^{(S)}_{n_1,n_2}(\boldsymbol{r}_1, \boldsymbol{r}_2) \\
(\hat{H}_1+\hat{H}_2) \chi^{(A)}_{n_1,n_2}(\boldsymbol{r}_1, \boldsymbol{r}_2) = (E_{n_1}+E_{n_2})
\chi^{(A)}_{n_1,n_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

\begin{align}
E_{n_1} = \frac{\hbar^2 \boldsymbol{k}_{n_1}^2}{2m_e} \ , \ E_{n_2} = \frac{\hbar^2 \boldsymbol{k}_{n_2}^2}{2m_e} \ , \ E = E_{n_1} + E_{n_2} \ , \ \omega = \frac{E}{\hbar}
\end{align}

自由空間内で２つの粒子を運動させよう！

上記の表式を用いて、自由空間内で２つの粒子を１次元上で運動させてみよう。展開係数を、それぞれの粒子の中心波数を $ k_{10} $ と $ k_{20} $ とするガウス分布

\begin{align}
c_{n_1, n_2} = e^{-\frac{1}{2}\left(\frac{k_{n_1}-k_{n_{10}}}{2\sigma}\right)^2} e^{-\frac{1}{2}\left(\frac{k_{n_2}-k_{n_{20}}}{2\sigma}\right)^2}
\end{align}

とした２つの波束を考えよう。

\begin{align}
\psi^{(S)}(x_1, x_2, t) &\ =\sum_{n_1,n_2} \left( e^{i k_{n_1}x_1 +i
k_{n_2}x_2} + e^{i k_{n_1}x_2 +i k_{n_2}x_1}\right) e^{-i\omega t}e^{-\frac{1}{2}\left(\frac{k_{n_1}-k_{n_{10}}}{2\sigma}\right)^2}
e^{-\frac{1}{2}\left(\frac{k_{n_2}-k_{n_{20}}}{2\sigma}\right)^2} \\
\psi^{(A)}(x_1, x_2, t) &\ =\sum_{n_1,n_2} \left( e^{i k_{n_1}x_1 +i
k_{n_2}x_2} – e^{i k_{n_1}x_2 +i k_{n_2}x_1}\right) e^{-i\omega t}e^{-\frac{1}{2}\left(\frac{k_{n_1}-k_{n_{10}}}{2\sigma}\right)^2}
e^{-\frac{1}{2}\left(\frac{k_{n_2}-k_{n_{20}}}{2\sigma}\right)^2}
\end{align}

この積分を数値的に計算することで、２つの粒子の時間発展を計算することができるよ。そして、粒子１あるいは粒子２が位置 $x$ に存在する確率を次のとおりに定義するよ。

\begin{align}
\rho(x) \equiv \int |\psi^{(S)}(x, x_2, t)|^2 dx_2 + \int |\psi^{(S)}(x_1, x, t)|^2 dx_1
\end{align}

次回、対称波動関数と反対称波動関数の違いを可視化するよ。

ポテンシャルが０のシュレーディンガー方程式の解である平面波は前回示したね。この平面波を重ね合わせることで、任意の波形を作ることができるよ。今回は、波数分布をガウス分布とした波束の作り方を解説するよ。波束は異なる波数（速度）の平面波の重ね合わせで作ることができるよ。中心波数 $k_0$ としたときの表式は次のとおりだよ。

\begin{align}
\psi(x,t)= \frac{1}{ \sqrt{2\sigma \pi L}}\int dk\, \exp\left[ ik(x-x_0) -i\omega t-\left(\frac{ k-k_0 }{2\sigma} \right)^2 \right]
\end{align}

$k_0$ は波束が進む速度 $v$ と、 $v_0 =p_0 / m_e = \hbar k_0 / m_e$ の関係があるよ。

波束の運動の計算結果

波束の中心エネルギー： $E_0 = 10[{\rm eV}]$
空間スケール： $10^{-11}[{\rm m}]$ //横軸の値
時間スケール： $10^{-16}[{\rm s}]$ //動画１コマの時間間隔

波束の中心エネルギー： $E_0 = 0[{\rm eV}]$
空間スケール： $10^{-11}[{\rm m}]$ //横軸の値
時間スケール： $4\times 10^{-15}[{\rm s}]$ //動画１コマの時間間隔

ちなみに、どんな波束も時間とともに広がっていくよ。その理由は分散関係 $\omega$ が $k$ に比例しないからだよ。

プログラムソース（C++）

////////////////////////////////////////////////////////////////////
// 【第３回】「波束」の作り方
////////////////////////////////////////////////////////////////////
#define _USE_MATH_DEFINES
#include <iostream>
#include <fstream>
#include <sstream>
#include <iomanip>
#include <string>
#include <complex>

/////////////////////////////////////////////////////////////////
//物理定数
/////////////////////////////////////////////////////////////////
//光速
const double c = 2.99792458E+8;
//真空の透磁率
const double mu0 = 4.0*M_PI*1.0E-7;
//真空の誘電率
const double epsilon0 = 1.0 / (4.0*M_PI*c*c)*1.0E+7;
//プランク定数
const double h = 6.6260896 * 1.0E-34;
double hbar = h / (2.0*M_PI);
//電子の質量
const double me = 9.10938215 * 1.0E-31;
//電子ボルト
const double eV = 1.60217733 * 1.0E-19;
//複素数
const std::complex<double> I = std::complex<double>(0.0, 1.0);
/////////////////////////////////////////////////////////////////
//物理系の設定
/////////////////////////////////////////////////////////////////
//空間分割数
const int Nx = 500;
//空間分割サイズ
double dx = 1.0E-10;
//重ね合わせの数
const int N = 200;
//パルスの幅
double delta_x = 1.0E-8;
double sigma = 2.0*sqrt(2.0*log(2.0)) / (delta_x);
//波数の間隔
double dk = 30.0 / (delta_x * double(N + 1));
//電子波のエネルギー
const double E0 = 10.0 * eV;
//波数の中心
double k0 = sqrt(2.0 * me * E0 / pow(hbar, 2));
//角振動数の中心
double omega0 = hbar / (2.0*me) * pow(k0, 2);

//計算時間の幅
const int ts = 0, te = 300;
//時間間隔
double dt = 1.0 * 1.0E-16;
/////////////////////////////////////////////////////////////////
const int precision_N = 4;

int main() {
	//出力ストリームによるファイルオープン
	std::ofstream fout;
	fout.open("wave.txt");
	fout << "#x:位置" << std::endl;
	fout << "#y:確率振幅" << std::endl;
	fout << "#legend: 実部 虚部 絶対値" << std::endl;
	fout << "#showLines: true true true" << std::endl;
	fout << "#showMarkers: false false false" << std::endl;
	fout << "#xrange:" << -Nx / 2 << " " << Nx / 2 << " " << Nx / 10 << std::endl;
	fout << "#yrange:" << -0.30 << " " << 0.30 << " " << 0.1 << std::endl;

	//各時刻における計算を行う
	for (int tn = ts; tn <= te; tn++) {
		double t_real = dt * double(tn);
		std::cout << tn << std::endl;
		fout << "#coma:" << tn << std::endl;

		for (int nx = 0; nx <= Nx; nx++) {
			double x = dx * (nx - Nx/2);
			std::complex<double> Psi = std::complex<double>(0.0, 0.0);
			for (int jz = 0; jz <= N; jz++) {
				double k = (k0 + dk * double(jz - N / 2));
				double omega = hbar / (2.0*me) * pow(k, 2);
				Psi += exp(I*(k*x - omega * t_real)) * exp(-1.0 / 2.0 * pow((k - k0) / sigma, 2));
			}
			Psi = Psi / double(N);
			fout << std::setprecision(precision_N);
			fout << x / dx << " " << Psi.real() << " " << Psi.imag() << " " << abs(Psi) << std::endl;
		}
		fout << std::endl;
	}
	fout.close();
}

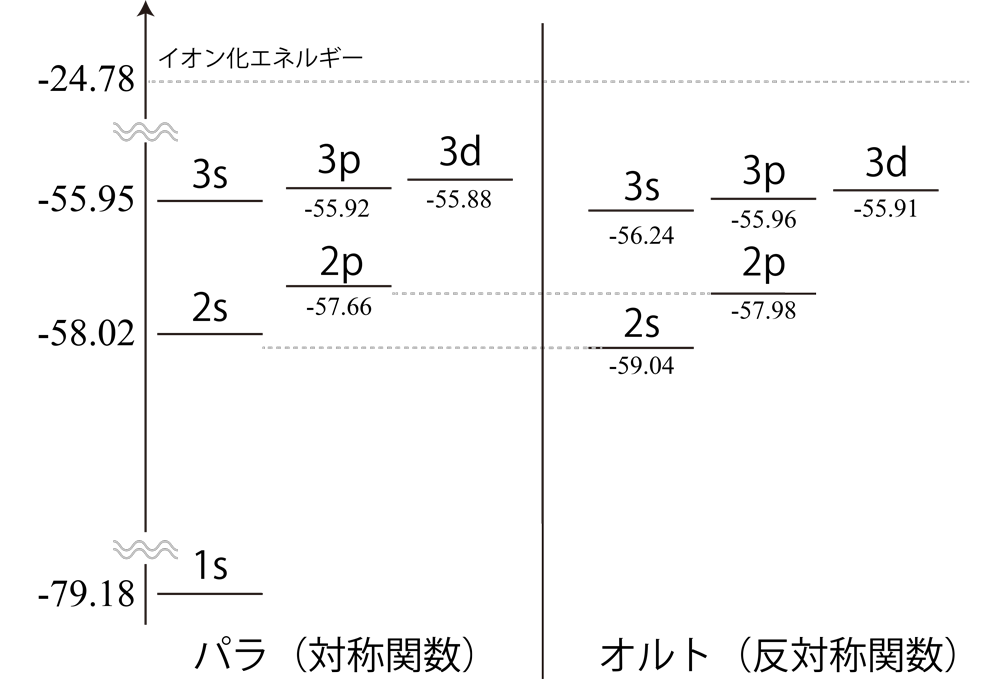
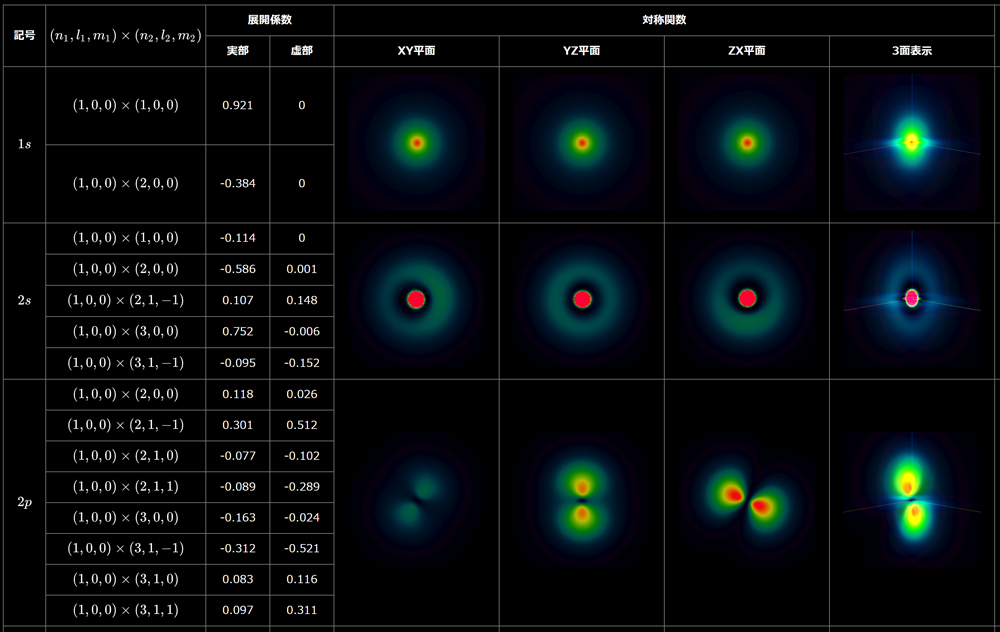
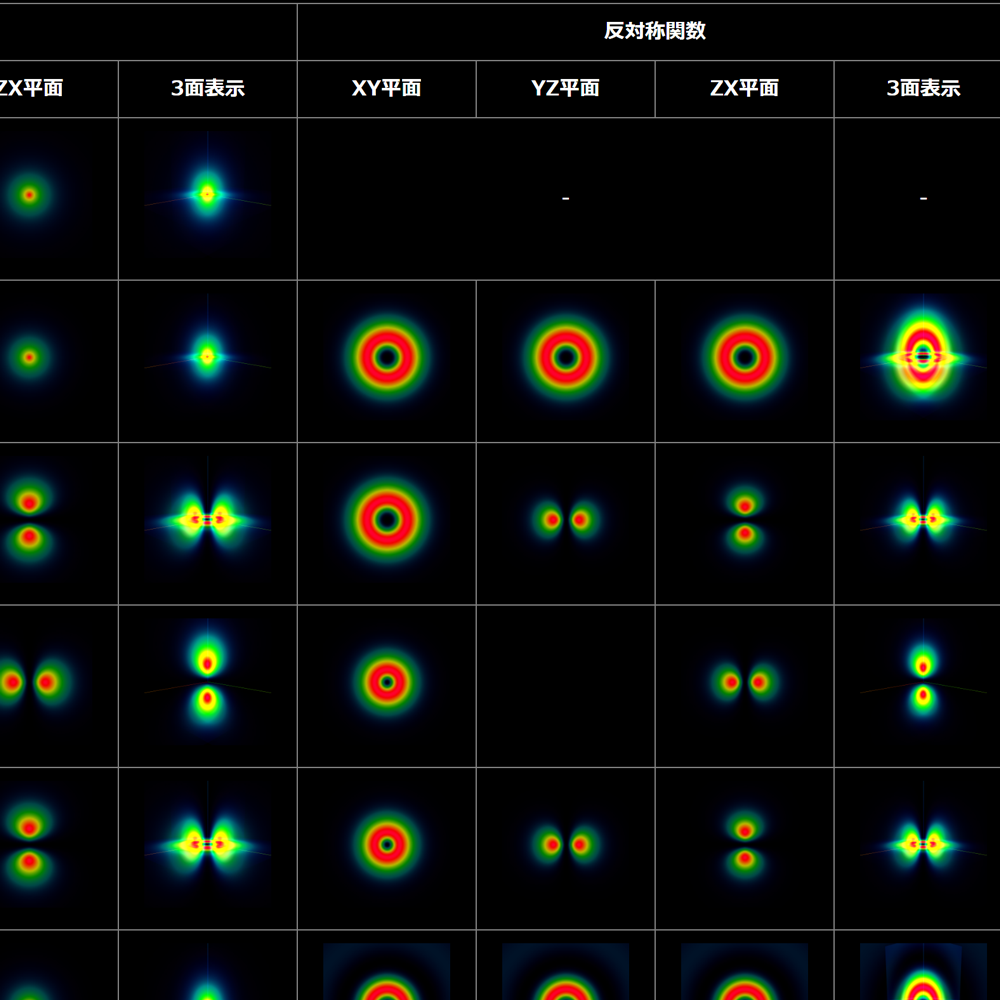
水素原子に束縛した電子の固有状態は解析的に計算することができるけれども、ヘリウム原子に束縛された２個の電子の固有状態は解析的には無理であることが知られているよ。ハミルトニアンは次のとおりだよ。

\begin{align}
H &\ = \frac{\hat{\boldsymbol{p}_1}^2}{2m_e} -\frac{q^2Z}{4\pi \epsilon_0|\boldsymbol{r}_1|} + \frac{\hat{\boldsymbol{p}_2}^2}{2m_e} -\frac{q^2Z}{4\pi \epsilon_0|\boldsymbol{r}_2|} + \frac{q^2}{4\pi \epsilon_0|\boldsymbol{r}_1-\boldsymbol{r}_2|}\\
&\ = H_1(\boldsymbol{r}_1) + H_2(\boldsymbol{r}_2) + H_{12}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

ハミルトニアンのうち、１番目の電子のみと２個目の電子のみに依存する部分をそれぞれ $H_1$、$H_2$ として、両電子に依存する部分を $H’$ とに分けているよ。この第３項目が存在することで、見た目よりも複雑だよ。このハミルトニアンの固有状態の数値計算方法でよく用いられるは、ハートリー＝フォック方程式と呼ばれる多電子系のシュレーディンガー方程式を平均場を導入することで１体問題と近似して計算する方法だね。今回は、平均場を導入することなしに２個の電子の固有状態を計算する方法を考えるよ。

空間対称関数と空間反対称関数を用いたエネルギー固有方程式

電子のようなフェルミ粒子は、スピン座標も含めた電子座標を入れ替えた固有状態は、反対称である必要があるね。そのため、空間部分はスピン座標が対称か非対称かによって、空間座標も対称か非対称しか取りえないね。

\begin{align}
\chi^{S}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_1(\boldsymbol{r}_1)\varphi_2(\boldsymbol{r}_2) + \varphi_1(\boldsymbol{r}_2)\varphi_2(\boldsymbol{r}_1) \right)\\
\chi^{A}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_1(\boldsymbol{r}_1)\varphi_2(\boldsymbol{r}_2) – \varphi_1(\boldsymbol{r}_2)\varphi_2(\boldsymbol{r}_1) \right)
\end{align}

展開する関数を、水素原子に束縛された電子の固有状態 $\varphi_{nlm}$ を用いると、

\begin{align}
\chi^{S}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_{nlm}(\boldsymbol{r}_1)\varphi_{n’l’m’}(\boldsymbol{r}_2) +
\varphi_{nlm}(\boldsymbol{r}_2)\varphi_{n’l’m’}(\boldsymbol{r}_1) \right)\\
\chi^{A}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_{nlm}(\boldsymbol{r}_1)\varphi_{n’l’m’}(\boldsymbol{r}_2) –
\varphi_{nlm}(\boldsymbol{r}_2)\varphi_{n’l’m’}(\boldsymbol{r}_1) \right)
\end{align}

と表すことができるね。今後の表記を簡単にするために量子数 $nlm$ をまとめて $\alpha $ と表すことにするね。

\begin{align}
\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) +
\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)\\
\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) –
\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)
\end{align}

$\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)$ と $\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)$ は、それぞれ異なる量子数のもとの次のような直交関係があるね。

\begin{align}
&\ \int\!\!\!\int \chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* \chi^{S}_{\alpha_3\alpha_4}(\boldsymbol{r}_1, \boldsymbol{r}_2) dV_1dV_2 \\
&\ =
\frac{1}{2}\int\!\!\!\int \left[ \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_2}^*(\boldsymbol{r}_2) + \varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_2}^*(\boldsymbol{r}_1) \right] \left[ \varphi_{\alpha_3}(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_2) + \varphi_{\alpha_3}(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_1) \right]dV_1dV_2 \\
&\ = \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int \varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2
+ \frac{1}{2}\int \varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2\\
&\ + \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2
+ \frac{1}{2}\int\varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2\\
&\ = \delta_{\alpha_1\alpha_3} \delta_{\alpha_2\alpha_4} + \delta_{\alpha_2\alpha_3} \delta_{\alpha_1\alpha_4}
\end{align}
\begin{align}
&\ \int\!\!\!\int \chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* \chi^{A}_{\alpha_3\alpha_4}(\boldsymbol{r}_1, \boldsymbol{r}_2) dV_1dV_2\\
&\ =
\frac{1}{2}\int\!\!\!\int \left[ \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_2}^*(\boldsymbol{r}_2) –
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_2}^*(\boldsymbol{r}_1) \right] \left[
\varphi_{\alpha_3}(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_2) –
\varphi_{\alpha_3}(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_1) \right]dV_1dV_2 \\
&\ = \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2
– \frac{1}{2}\int \varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2\\
&\ – \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2
+ \frac{1}{2}\int\varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2\\
&\ = \delta_{\alpha_1\alpha_3} \delta_{\alpha_2\alpha_4} – \delta_{\alpha_2\alpha_3} \delta_{\alpha_1\alpha_4}
\end{align}

\begin{align}
&\ \int\!\!\!\int \chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* \chi^{A}_{\alpha_3\alpha_4}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 \\
&\ =
\frac{1}{2}\int\!\!\!\int \left[ \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_2}^*(\boldsymbol{r}_2) +
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_2}^*(\boldsymbol{r}_1) \right] \left[
\varphi_{\alpha_3}(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_2) –
\varphi_{\alpha_3}(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_1) \right]dV_1dV_2 \\
&\ = \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2
+ \frac{1}{2}\int \varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2\\
&\ – \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2
– \frac{1}{2}\int\varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2\\
&\ = 0
\end{align}
\begin{align}
&\ \int\!\!\!\int \chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* \chi^{S}_{\alpha_3\alpha_4}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 \\
&\ =
\frac{1}{2}\int\!\!\!\int \left[ \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_2}^*(\boldsymbol{r}_2) –
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_2}^*(\boldsymbol{r}_1) \right] \left[
\varphi_{\alpha_3}(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_2) +
\varphi_{\alpha_3}(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_1) \right]dV_1dV_2 \\
&\ = \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2
– \frac{1}{2}\int \varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2\\
&\ + \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2
– \frac{1}{2}\int\varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2\\
&\ = 0
\end{align}

対称関数の場合、$ \alpha_1 = \alpha_2 = \alpha_3 = \alpha_4 $ を満たす時に上記の直交積分は「２」になってしまうので、条件に応じて定義を変えておく必要があるね。

\begin{align}
\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \left\{ \matrix{ \varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha}(\boldsymbol{r}_2) & \alpha = \alpha’ \cr \frac{1}{\sqrt{2}} \left( \varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) +\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right) & \alpha \ne \alpha’}\right.
\end{align}

$\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)$ と $\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)$ を構成する関数は、元々正規直交完全系を成す関数系なので、この対称関数と反対称関数を新たな基底関数とする正規直交系を考えることができるね。つまり、ヘリウム原子の電子に対する波動関数を

\begin{align}
\psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \sum_{\alpha,\alpha’}
s_{\alpha\alpha’}\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) \\
\psi^{(A)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \sum_{\alpha,\alpha’}
a_{\alpha\alpha’}\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) \\
\end{align}

として、ハミルトニアンによる固有方程式

\begin{align}
H\psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = E \psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) \\
H\psi^{(A)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = E \psi^{(A)}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

からエネルギー固有状態を考えることができそうだね。

ハミルトニアンと対称関数・反対称関数との関係

エネルギー固有状態を計算するために必要な、各項の関係をまずは押さえておこう。対称関数は、ハミルトニアン $H_1$ と $H_2$ とは

\begin{align}
H_1 \chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( E_{\alpha}\varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) +E_{\alpha’}\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)\\
H_2 \chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( E_{\alpha’}\varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) +E_{\alpha}\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)
\end{align}

のように固有状態にはなっていないけれども、足し算すると

\begin{align}
(H_1 + H_2)\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) = ( E_{\alpha}+ E_{\alpha’})\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

というふうに、エネルギー固有状態になっているね。同様に、反対称関数の場合も

\begin{align}
H_1 \chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( E_{\alpha}\varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) – E_{\alpha’}\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)\\
H_2 \chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( E_{\alpha’}\varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) – E_{\alpha}\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)
\end{align}

となるので、足し算すると

\begin{align}
(H_1 + H_2)\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) = ( E_{\alpha} + E_{\alpha’})\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

というふうに、エネルギー固有状態になっているね。つまり、ハミルトニアンの前半２つの項は、これら対称関数と反対称関数で固有状態となっているので、これまで水素原子に外場を加えたときの固有状態を計算したときの手順がそのまま適用できそうだね。 エネルギー固有方程式

\begin{align}
\sum_{\alpha,\alpha’} (H_1 + H_2 + H_{12}) s_{\alpha\alpha’}\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1,
\boldsymbol{r}_2) &\ = E
\sum_{\alpha,\alpha’} s_{\alpha\alpha’}\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) \\
\sum_{\alpha,\alpha’} (H_1 + H_2 + H_{12})a_{\alpha\alpha’}\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = E
\sum_{\alpha,\alpha’} a_{\alpha\alpha’}\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

の両辺に $\chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* $ と $\chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* $をそれぞれ掛けて、全空間で積分すると、

\begin{align}
s_{\alpha_1\alpha_2} (E_1 + E_2) +
\sum_{\alpha,\alpha’} s_{\alpha\alpha’} \int\!\!\!\int \chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* H_{12} \chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 &\ = E s_{\alpha_1\alpha_2} \\
a_{\alpha_1\alpha_2} (E_1 + E_2)
+\sum_{\alpha,\alpha’}a_{\alpha\alpha’}\int\!\!\!\int \chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* H_{12} \chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 &\ = E a_{\alpha_1\alpha_2}
\end{align}

となるね。これらは $s_{\alpha_1\alpha_2}$ $a_{\alpha_1\alpha_2}$ に関する連立方程式になるので、あとは数値計算でこれらの値を計算するだけだね。ちなみに対称と反対称のペアの積分は次の通りゼロだね。

\begin{align}
\int\!\!\!\int \chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* H_{12}
\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 &\ = 0 \\
\int\!\!\!\int \chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* H_{12}
\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 &\ = 0
\end{align}

次回、ヘリウム原子のエネルギー準位の計算結果を示すよ。