ヘリウム原子のエネルギー準位と固有関数の空間分布（直交系展開によるエネルギー固有状態の計算結果）

「ヘリウム原子のエネルギー固有状態の計算方法」に基づいて、ヘリウム原子のエネルギー準位と固有関数の空間分布を計算したよ。「ヘリウム原子の基底状態の計算結果」で示したとおり、計算結果はよく知られた精密な実験結果とかなり一致しているよ。

ヘリウム原子のエネルギー準位

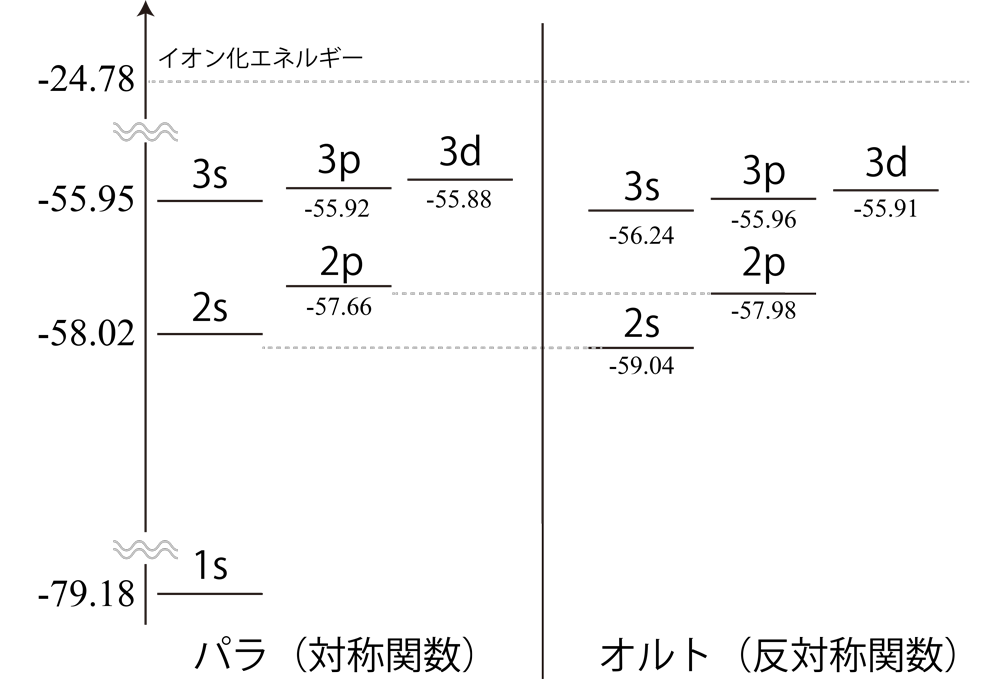
次の図は、パラ（対称関数・スピン１重項）とオルト（反対称関数・スピン３重項）の主量子数 $n=1,2,3$
のエネルギー準位だよ。オルトのほうがパラよりも若干小さな値となるね。これは交換相互作用の結果だね。イオン化エネルギーは、電子２個の基底状態から電子１個を引き離すために必要なエネルギーで、「基底状態エネルギー（$-79.18[{\rm
eV}]$）」から「電子が１個のみのヘリウム原子の基底状態エネルギー（ $-54.4[{\rm eV}]$ ）」で計算できるよ。

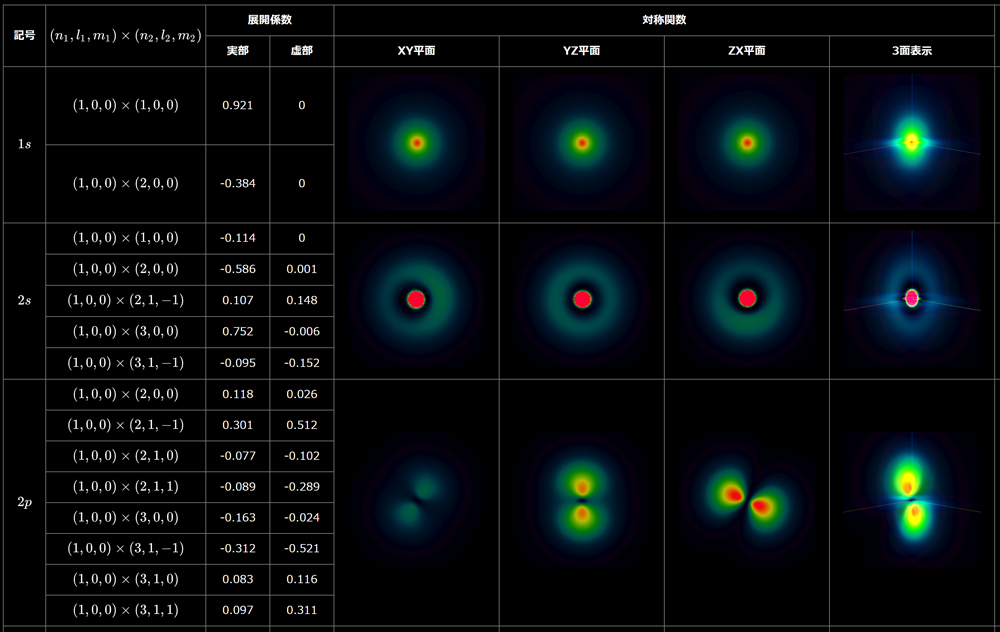
ヘリウム原子の固有状態の空間分布

今回も独立電子近似の場合と同様、粒子の１つが
$\varphi_{100}(\boldsymbol{r})|$の最も確率の高い原点（ $\boldsymbol{r}_1=0$ あるいは $\boldsymbol{r}_2=0$
）に存在するとして、他方の粒子の空間確率密度を描画するよ。最初の表がパラヘリウム（対称関数・スピン1重項）、次の表がオルトヘリウム（反対称関数・スピン3重項）だよ。

（※実際の表はこちらのページを見てね！）

ちなみにヘリウム原子の場合、直交関数系は $(1,0,0)$ を必ず含むよ。なぜならば、$(1,0,0)$ から次に低い $(2,0,0)$ とした場合の固有エネルギーは約 $-20[{\rm eV}]$
で、イオン化エネルギーよりも高くなるために実質的には先に電離してしまうね。