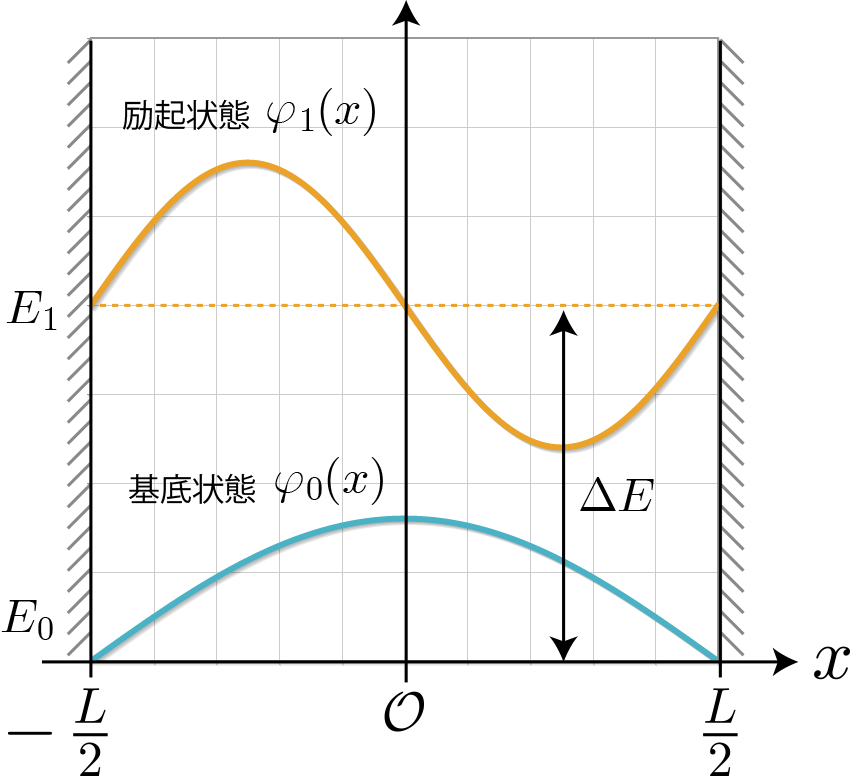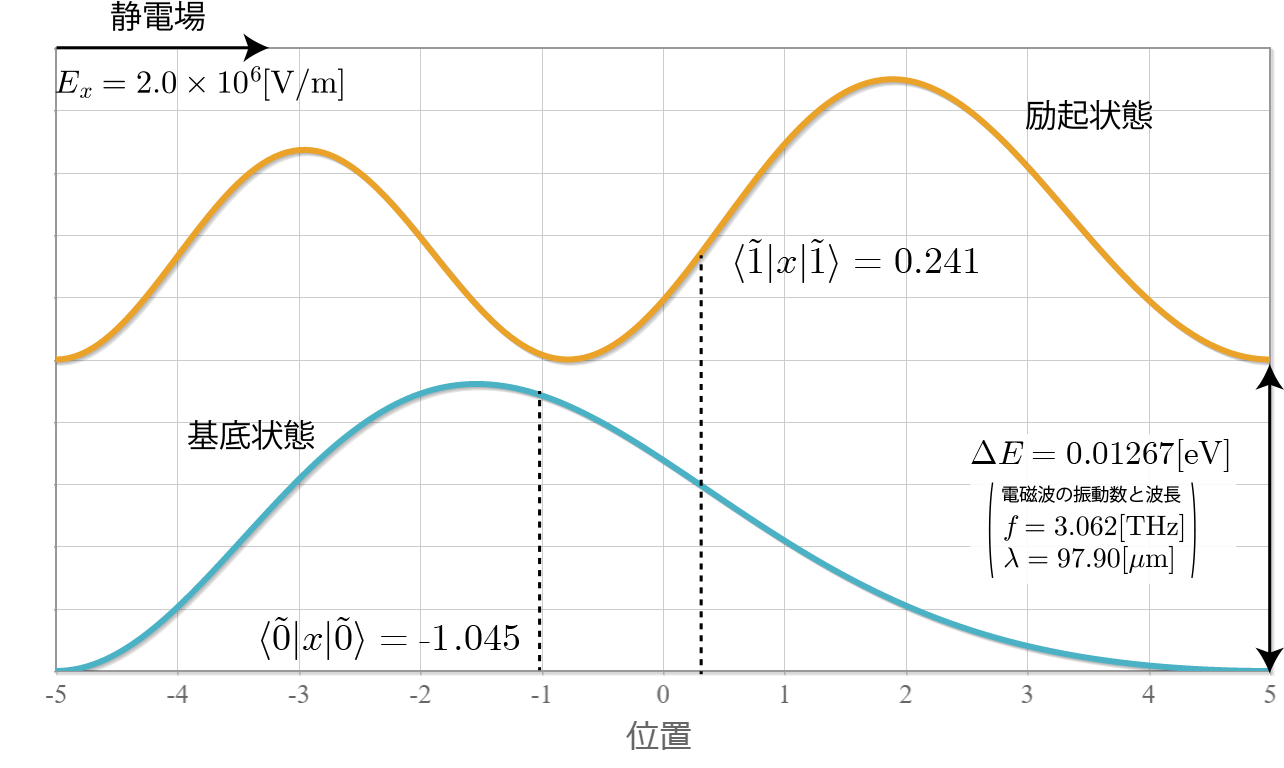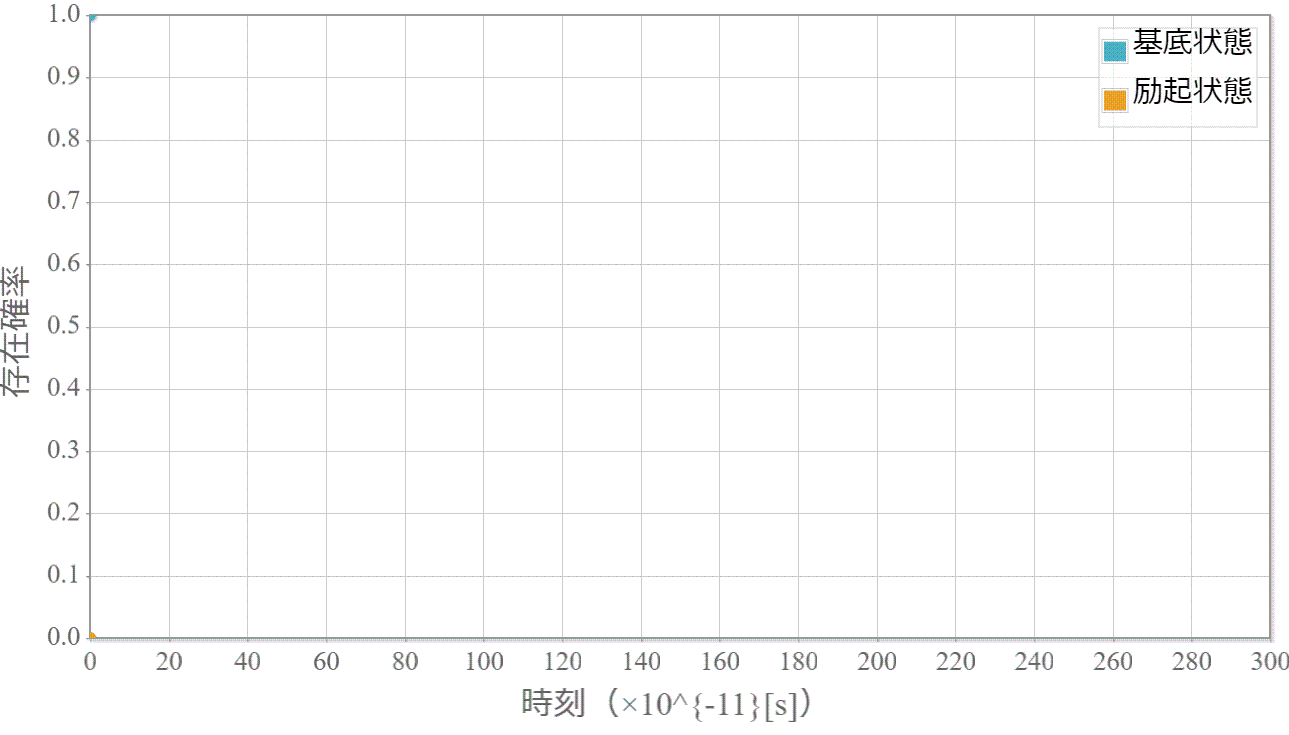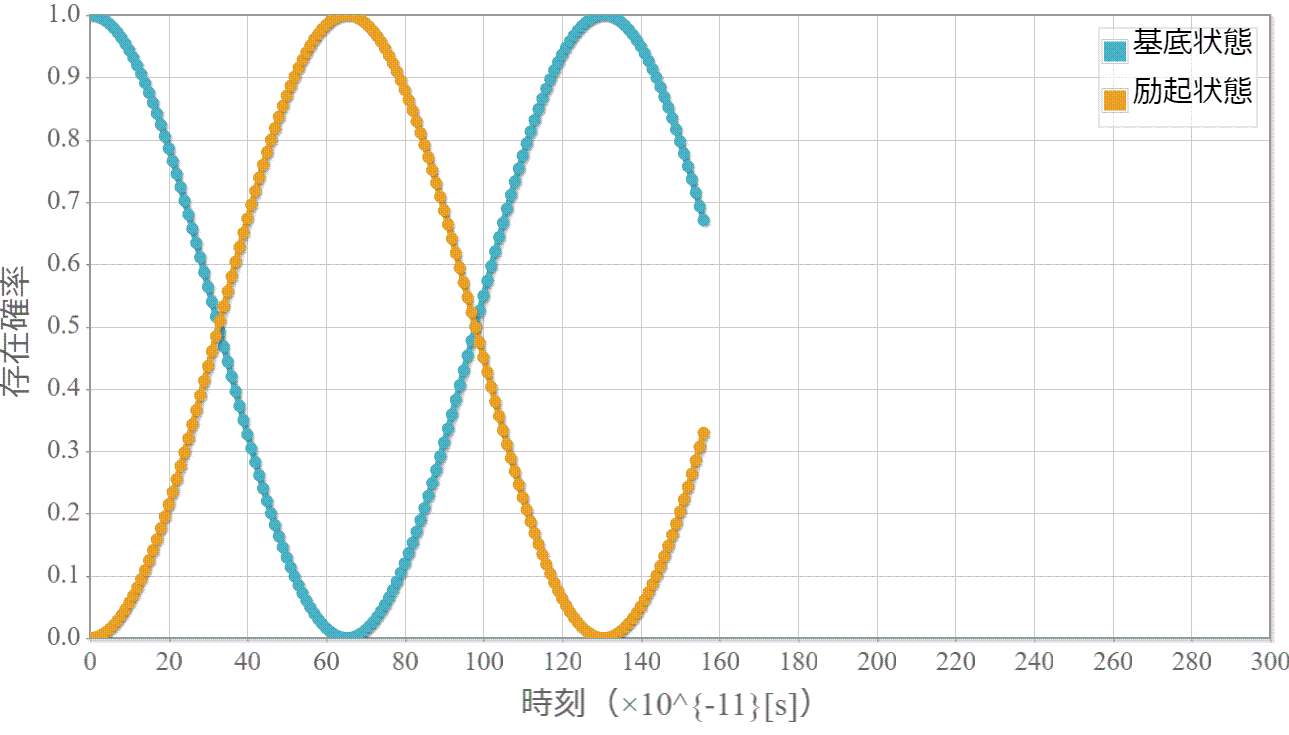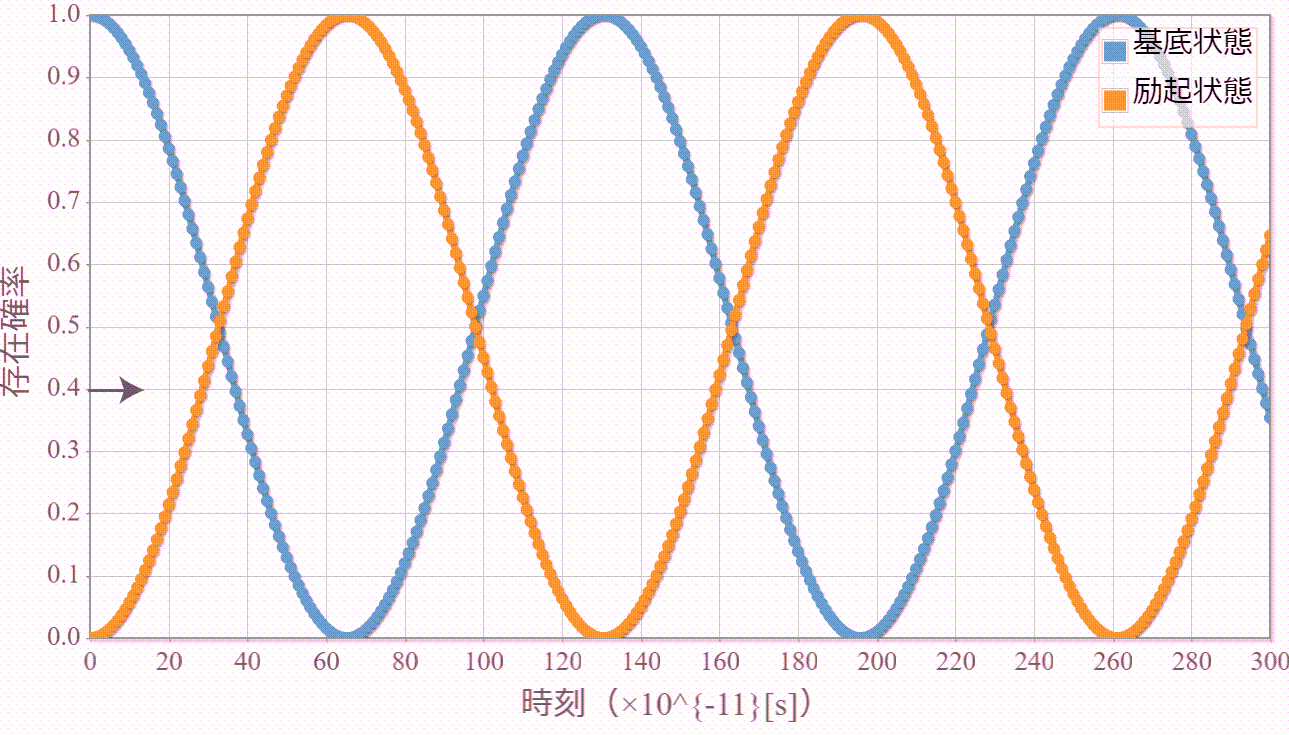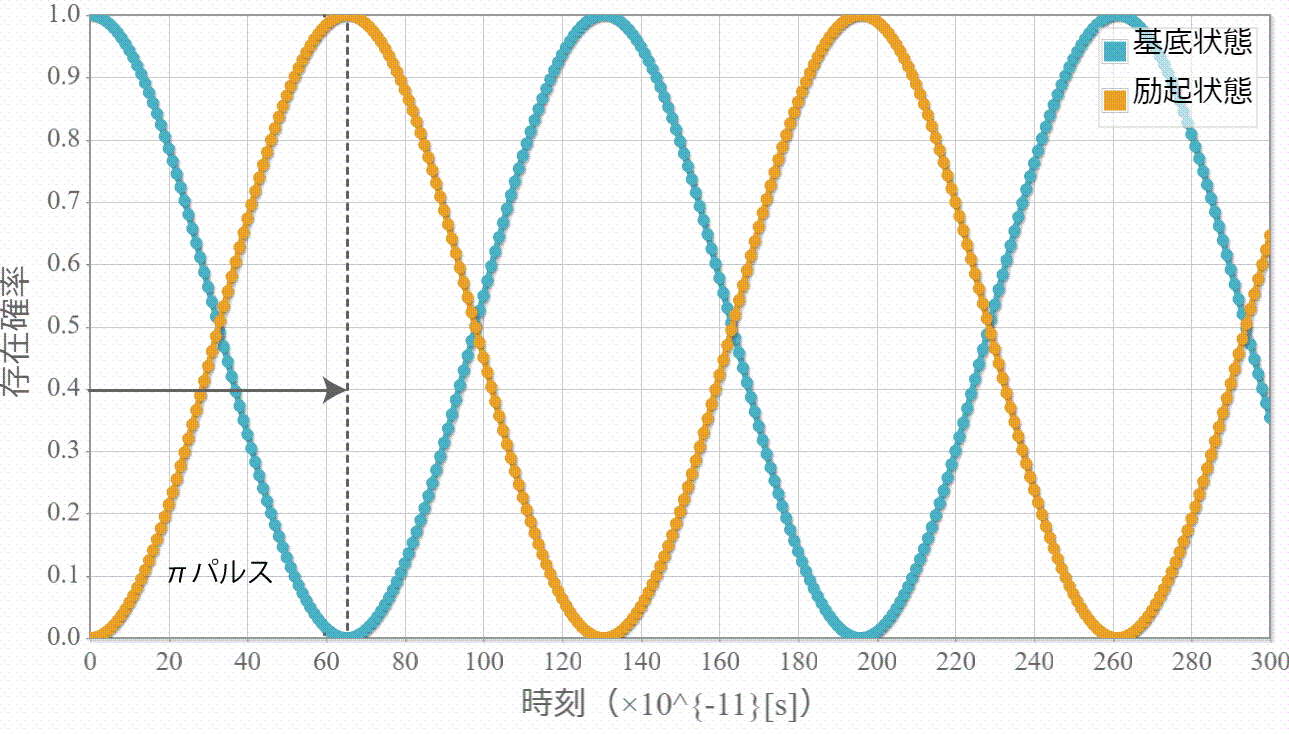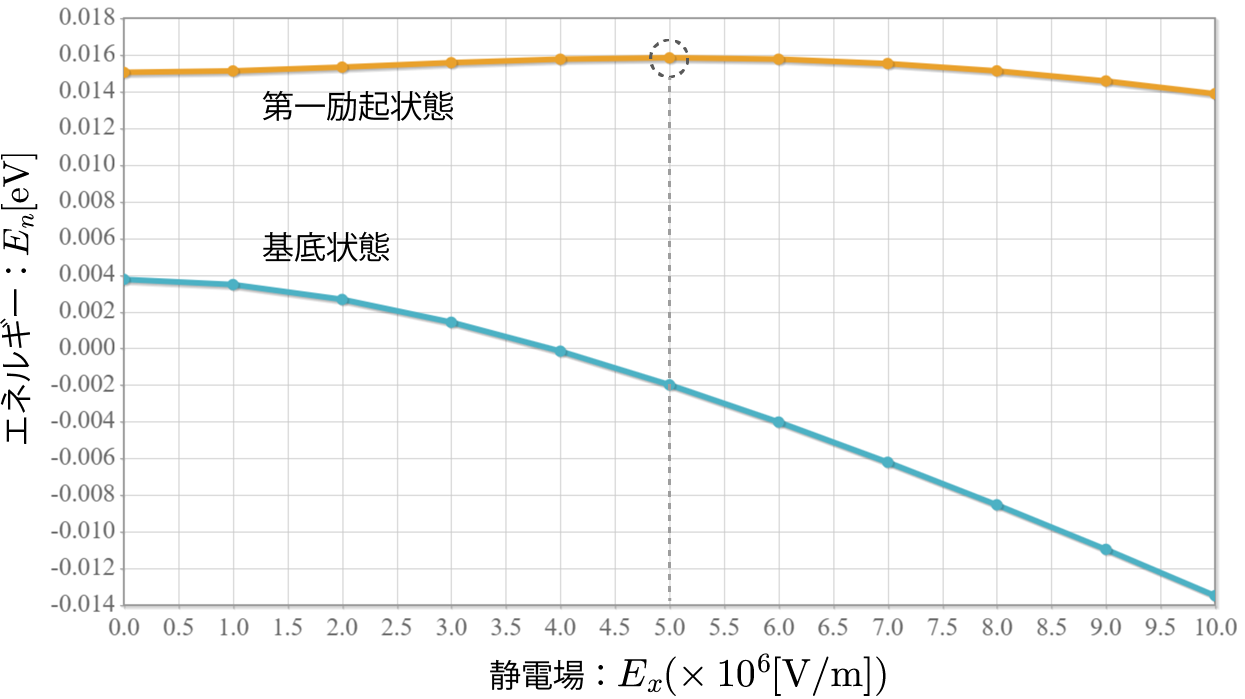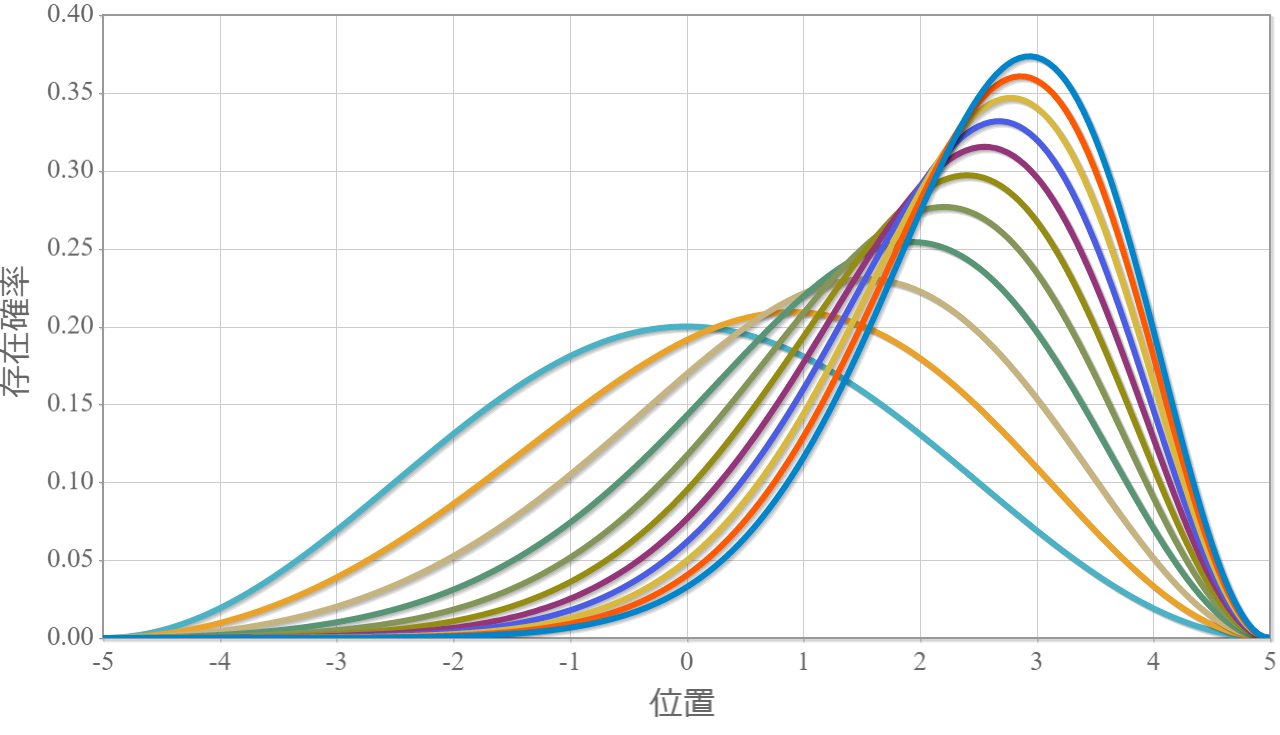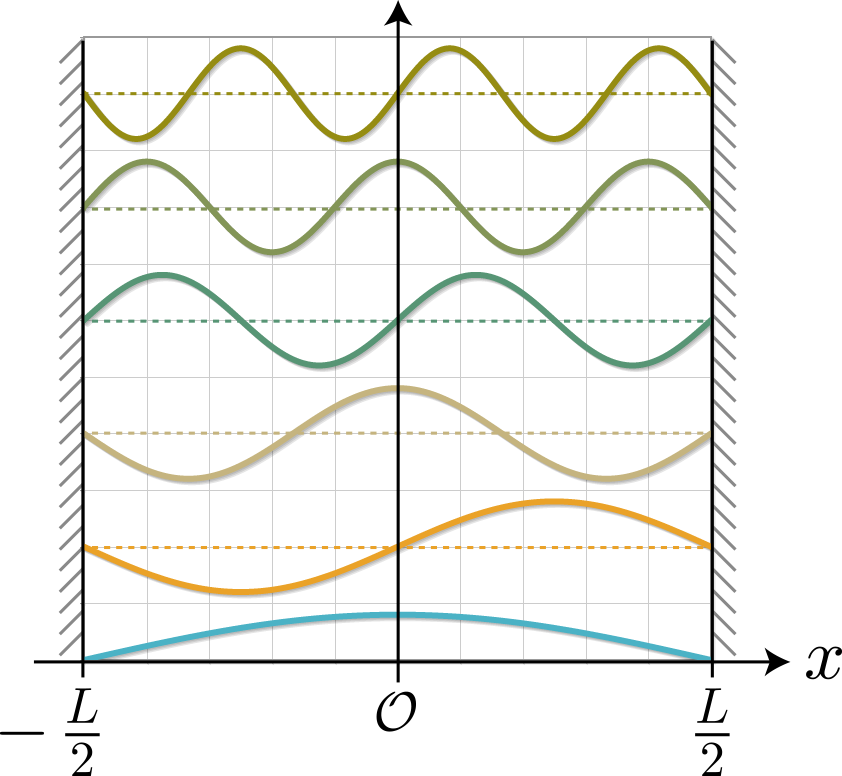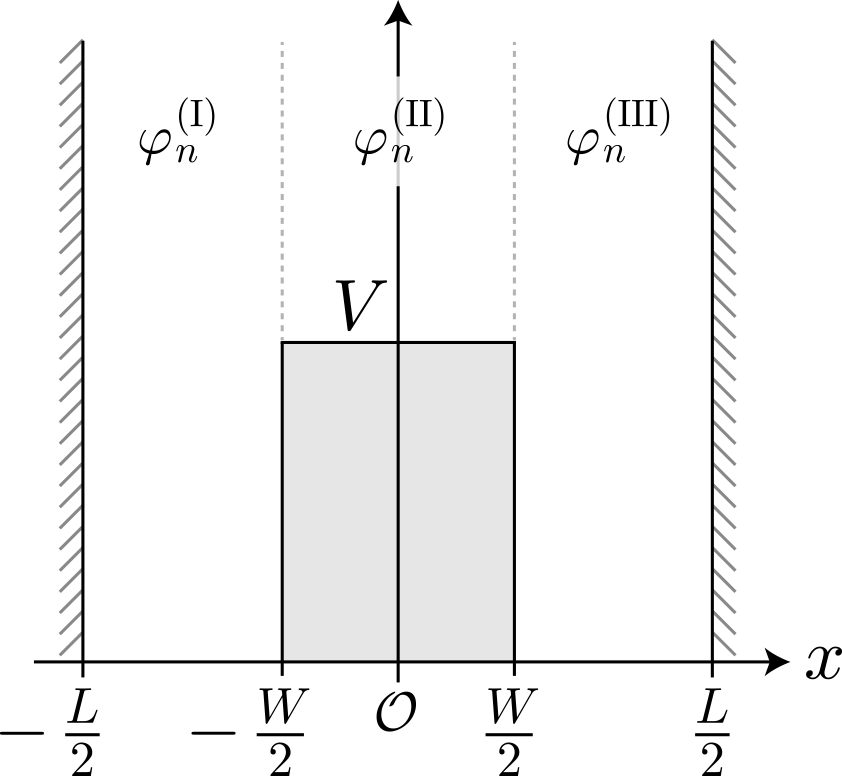
1量子ビットに対応する量子ドットに対するシミュレーションをこれまでやってきたけれども、2量子ビットに対応する2重量子ドットに束縛された電子の固有状態を調べるよ。具体的には右図のように1次元の幅 $L$ の量子井戸の真ん中に幅 $W$ のポテンシャル障壁を作って、2個の電子がそれぞれに配置されるような状況を考えたいけれども、今回はその準備として、電子が1個の場合を固有状態の計算方法を示すよ。
固有状態の計算方法
図のような無限に高い井戸型ポテンシャル内に壁があるような場合、ポテンシャルの大きさによって空間領域を3つに分けて、それぞれの領域$(\rm I), (II), (III)$で右向きと左向きの平面波が存在すると仮定して、
\begin{align}
\varphi^{(\rm I)}_n (x) &\ = A e^{ik^{(\rm I)}(x+\frac{W}{2})} + B e^{-ik^{(\rm I)}(x+\frac{W}{2})} \ \ \ (-\frac{L}{2} \leq x\leq -\frac{W}{2} ) \\
\varphi^{(\rm II)}_n (x) &\ = C e^{ik^{(\rm II)}x} + D e^{-ik^{(\rm II)}x} \ \ \ (-\frac{W}{2} \leq x\leq \frac{W}{2} ) \\
\varphi^{(\rm III)}_n (x) &\ = E e^{ik^{(\rm III)}(x-\frac{W}{2})} + F e^{-ik^{(\rm III)}(x-\frac{W}{2})} \ \ \ (\frac{W}{2} \leq x\leq \frac{L}{2} ) \\
\end{align}
と表しておいて、各領域間の境界条件
\begin{align}
\varphi^{(\rm I)}_n (-\frac{L}{2}) = 0 \ &\ , \ \varphi^{(\rm III)}_n (\frac{L}{2}) = 0\\
\varphi^{(\rm I)}_n (-\frac{W}{2}) = \varphi^{(\rm II)}_n (-\frac{W}{2}) \ &\ , \ \left.\frac{d\varphi^{(\rm I)}_n (x)}{d x}\right|_{x=-\frac{W}{2}} = \left.\frac{d \varphi^{(\rm II)}_n (x)}{d x}\right|_{x=-\frac{W}{2}} \\
\varphi^{(\rm II)}_n (\frac{W}{2}) = \varphi^{(\rm III)}_n (\frac{W}{2}) \ &\ , \ \left.\frac{d\varphi^{(\rm II)}_n (x)}{d
x}\right|_{x=\frac{W}{2}} = \left.\frac{d \varphi^{(\rm III)}_n (x)}{d x}\right|_{x=\frac{W}{2}}
\end{align}
を課すことで、係数($A, B, C, D, E, F$)の関係を導出するよ。ただし、それぞれの領域の平面波の波数は電子のエネルギー $E$ に対して
\begin{align}
k^{(\rm I)} = \frac{\sqrt{2m_eE}}{\hbar} \ , \ k^{(\rm II)} = \frac{\sqrt{2m_e(E-V)}}{\hbar} \ , \ k^{(\rm III)} = \frac{\sqrt{2m_eE}}{\hbar}
\end{align}
を満たすよ。そのため、$k^{(\rm I)} = k^{(\rm III)}$ であることがわかるね。
(1)$x= -L/2$ の境界条件
領域(I)の波動関数 $\varphi^{(\rm I)}_n (x)$ に$x= -L/2$ の境界条件を課してみよう!
\begin{align}
A e^{-ik^{(\rm I)}(\frac{L}{2} – \frac{W}{2})} + B e^{ik^{(\rm I)}(\frac{L}{2} – \frac{W}{2})} &\ = 0 \\
&\ \downarrow \\
(A+B) \cos\left[k^{(\rm I)}\left(\frac{L}{2} – \frac{W}{2}\right)\right] + i (-A+B) \sin\left[k^{(\rm I)}\left(\frac{L}{2} – \frac{W}{2}\right)\right] &\ = 0\\
\end{align}
となることから、これを満たす非自明な解($A=0, B=0$以外の解)は、
\begin{align}
A = B \ , \ k^{(\rm I)}\left(\frac{L}{2} – \frac{W}{2}\right) = \pi \left(n +\frac{1}{2} \right)
\end{align}
あるいは
\begin{align}
A = -B \ , \ k^{(\rm I)}\left(\frac{L}{2} – \frac{W}{2}\right) = \pi(n+1)
\end{align}
を満たす必要があるね($n=0,1,2,3,\cdots$)。両者はそれぞれ
\begin{align}
\varphi^{(\rm I)}_n (x) &\ = 2A \cos \left[ \frac{ 2\pi\left(n +\frac{1}{2} \right)}{L-W} \left(x +\frac{W}{2} \right) \right] = -2A \sin \left[ \frac{ 2\pi\left(n +\frac{1}{2} \right)}{L-W} \left(x +\frac{L}{2} \right) – \pi n\right] \\
\varphi^{(\rm I)}_n (x) &\ = 2iB \sin \left[ \frac{2\pi (n+1)}{L – W} \left(x +\frac{W}{2} \right) \right] = -2iB \sin \left[ \frac{2\pi (n+1)}{L – W} \left(x +\frac{L}{2} \right) – \pi (n+1) \right]
\end{align}
となるけれども、$\sin$ 関数内の波数に対応する部分に着目すると、前者の($2n+1$)は奇数、後者のの($2(n+1)$)は偶数を表すので、結局は両者を合わせると0を含めた全自然数となるね。係数は改めて置き直して、
\begin{align}
\varphi^{(\rm I)}_n (x) &\ = A_n \sin \left[ k^{(\rm I)}_n \left(x +\frac{L}{2} \right) \right] \ , \ k^{(\rm I)}_n = \frac{\pi(n+1)}{L- W}
\end{align}
となるね($n=1,2,3,\cdots$)。この関係からエネルギーも離散化されて
\begin{align}
E_n = \frac{\hbar^2 {k^{(I)}_n}^2}{2m_e} = \frac{\hbar^2}{2m_e} \left[ \frac{\pi(n+1)}{L- W}\right]^2
\end{align}
であることもわかるね。
(2)$x= L/2$ の境界条件
領域(III)の波動関数 $\varphi^{(\rm III)}_n (x)$ に$x= L/2$ の境界条件を課した結果も、先と全く同様となるね。対称性を考慮してかつ係数を改めて $F_n$ と置いておくよ。
\begin{align}
\varphi^{(\rm III)}_n (x) &\ = F_n \sin \left[ k^{(\rm III)}_n \left(x -\frac{L}{2} \right) \right] \ , \ k^{(\rm III)}_n = \frac{\pi(n+1)}{L- W}
\end{align}
(3)$x= -\frac{W}{2}$ の境界条件
領域(I)と領域(II)の2つの波動関数の境界条件を課してみよう!
\begin{align}
\varphi^{(\rm I)}_n (-\frac{W}{2}) = \varphi^{(\rm II)}_n (-\frac{W}{2}) \ &\ \longrightarrow \ A_n \sin \left[ k^{(\rm I)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] = C e^{-ik^{(\rm II)}\frac{W}{2}} + D e^{ik^{(\rm II)}\frac{W}{2}} \\
\left.\frac{d\varphi^{(\rm I)}_n (x)}{d x}\right|_{x=-\frac{W}{2}} = \left.\frac{d \varphi^{(\rm II)}_n (x)}{d x}\right|_{x=-\frac{W}{2}} \ &\ \longrightarrow \ A_n k^{(\rm I)}_n \cos \left[ k^{(\rm I)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] = i C k^{(\rm II)} e^{-ik^{(\rm II)}\frac{W}{2}} – iD k^{(\rm II)} e^{ik^{(\rm II)}\frac{W}{2}}
\end{align}
前者の両辺に $i k^{(\rm II)}$ を掛け算した後に、前者と後者を足し引きすると、
\begin{align}
C_n &\ = \frac{A_n}{2i} e^{ik_n^{(\rm II)}\frac{W}{2}} \left\{i\sin \left[ k^{(\rm I)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] + \frac{k^{(\rm I)}_n}{k_n^{(\rm II)}} \cos \left[ k^{(\rm I)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] \right\} \\
&\ = \frac{A_n}{2i} e^{ik_n^{(\rm II)}\frac{W}{2}} \left\{ i\cos \left( \frac{\pi n}{2}\right) – \frac{k^{(\rm I)}_n}{k_n^{(\rm II)}} \sin \left( \frac{\pi n}{2}\right)\right\} \\
D_n &\ = \frac{A_n }{2i} e^{-ik_n^{(\rm II)}\frac{W}{2}} \left\{i\sin \left[ k^{(\rm I)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] – \frac{k^{(\rm I)}_n}{k_n^{(\rm II)}} \cos \left[ k^{(\rm I)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] \right\} \\
&\ = \frac{A_n}{2i} e^{-ik_n^{(\rm II)}\frac{W}{2}} \left\{ i\cos \left( \frac{\pi n}{2}\right) + \frac{k^{(\rm I)}_n}{k_n^{(\rm II)}} \sin \left( \frac{\pi n}{2}\right)\right\}
\end{align}
という風に $A_n$で表すことができるね。ちなみに、波数 $k^{(\rm II)}_n$ は離散化したエネルギーと直接関係があるね。
\begin{align}
k^{(\rm II)}_n = \frac{\sqrt{2m_e(E_n – V)}}{\hbar}
\end{align}
$k^{(\rm II)}_n = 0$ の場合
電子のエネルギーがちょうど壁のポテンシャルエネルギーと同じ場合、領域(II)の波数は $k^{(\rm II)}_n = 0$ となるね。その場合の扱いは別途行う必要があるね。
\begin{align}
A_n \cos \left( \frac{\pi n}{2}\right) &\ = C_n + D_n \\
-A_n k^{(\rm I)}_n \sin\left( \frac{\pi n}{2}\right) &\ = 0
\end{align}
となるね。
(4)$x= \frac{W}{2}$ の境界条件
最後に、領域(II)と領域(III)の2つの波動関数の境界条件を課してみよう!
\begin{align}
\varphi^{(\rm II)}_n (\frac{W}{2}) = \varphi^{(\rm III)}_n (\frac{W}{2}) \ &\ \longrightarrow \ C e^{ik^{(\rm II)}\frac{W}{2}} + D e^{-ik^{(\rm II)}\frac{W}{2}} = F_n \sin \left[ k^{(\rm III)}_n \left(\frac{W}{2} – \frac{L}{2} \right) \right] \\
\left.\frac{d\varphi^{(\rm II)}_n (x)}{d x}\right|_{x=\frac{W}{2}} = \left.\frac{d \varphi^{(\rm III)}_n (x)}{d x}\right|_{x=\frac{W}{2}} \ &\ \longrightarrow \ iC k^{(\rm II)} e^{ik^{(\rm II)}\frac{W}{2}} – iD k^{(\rm II)} e^{-ik^{(\rm II)}\frac{W}{2}} = F_n k^{(\rm III)}_n \cos \left[ k^{(\rm III)}_n \left(\frac{W}{2} – \frac{L}{2} \right) \right]
\end{align}
前者の両辺に $i k^{(\rm II)}$ を掛け算した後に、前者と後者を足し引きすると、
\begin{align}
C_n &\ = \frac{F_n}{2i} e^{-ik_n^{(\rm II)}\frac{W}{2}} \left\{-i\sin \left[ k^{(\rm III)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] + \frac{k^{(\rm III)}_n}{k_n^{(\rm II)}} \cos \left[ k^{(\rm III)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] \right\} \\
&\ = \frac{F_n}{2i} e^{-ik_n^{(\rm II)}\frac{W}{2}} \left\{ -i\cos \left( \frac{\pi n}{2}\right) – \frac{k^{(\rm III)}_n}{k_n^{(\rm II)}} \sin \left( \frac{\pi n}{2}\right)\right\} \\
D_n &\ = \frac{F_n }{2i} e^{ik_n^{(\rm II)}\frac{W}{2}} \left\{-i\sin \left[ k^{(\rm III)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] – \frac{k^{(\rm III)}_n}{k_n^{(\rm II)}} \cos \left[ k^{(\rm III)}_n \left(-\frac{W}{2} + \frac{L}{2} \right) \right] \right\} \\
&\ = \frac{F_n}{2i} e^{ik_n^{(\rm II)}\frac{W}{2}} \left\{ -i\cos \left( \frac{\pi n}{2}\right) + \frac{k^{(\rm III)}_n}{k_n^{(\rm II)}} \sin \left( \frac{\pi n}{2}\right)\right\}
\end{align}
という風に $F_n$で表すことができるね。
$k^{(\rm II)}_n = 0$ の場合
今回も電子のエネルギーがちょうど壁のポテンシャルエネルギーと同じになる場合の $k^{(\rm II)}_n = 0$ の扱いを別途行う必要があるね。
\begin{align}
– F_n \cos \left( \frac{\pi n}{2}\right) &\ = C_n + D_n \\
-F_n k^{(\rm III)}_n \sin\left( \frac{\pi n}{2}\right) &\ = 0
\end{align}
となるけれども、これだけでは $C_n$ と $D_n$ は決定できないね。
係数の関係を決定しよう!
今回、指数 $n$ によって係数の位相が異なるので、個別に計算する必要があるので、まずは $n=0$ の場合を計算してみるよ。$C_0, D_0$ と $A_0$ の関係は次のとおりだよ。
\begin{align}
C_0 &\ = \frac{A_0}{2} e^{ik^{(II)}_0 \frac{W}{2}} \\
D_0 &\ = \frac{A_0}{2} e^{-ik^{(II)}_0 \frac{W}{2}}
\end{align}
一方、$C_0, D_0$ と $F_0$ の関係は
\begin{align}
C_0 &\ = -\frac{F_0}{2} e^{-ik^{(II)}_0 \frac{W}{2}} \\
D_0 &\ = -\frac{F_0}{2} e^{ik^{(II)}_0 \frac{W}{2}}
\end{align}
となるけれども、先の結果と合わせて $F_0$ と $A_0$ の関係を求めると、考えると自明だけれども面白いことがわかるよ。$C_0$ を消去して得られる関係と、$D_0$ を消去して得られる関係はそれぞれ
\begin{align}
F_0 &\ = -A_0 e^{ik^{(II)}_0 W}\\
F_0 &\ = -A_0 e^{-ik^{(II)}_0 W}
\end{align}
となることから、なんと、$F_0$ と $A_0$ が0以外の解を持つには、
\begin{align}
k^{(II)}_0 W = 2\pi m \ \longrightarrow \ \frac{ \sqrt{2m_e (E_0 – V)} }{\hbar} W = 2\pi m
\end{align}
と、$V$ または $W$ に制限が加わることを意味するね($m = 0, 1, 2, \cdots$ )。これは「領域(II)の両端でうまく境界条件を満たすには、位相の変化分(波数×距離)が特定の条件を満たす必要がある」ことを意味しているね。よく考えれば自明だけれども、ちょっと意外だったね。次回は、この2重井戸の固有状態を可視化するよ。