前回を踏まえて、ヘリウム原子基底状態の動径確率密度分布を計算したので、報告するよ。次のグラフでは、ヘリウム原子基底状態に対する動径確率密度分布は2種類用意したよ。1つ目は「2つの電子のどちらかがその距離にいる確率密度( 青色:$\bar{P}_{100}^{Z=2}(r) $ )」、2つ目は「1つの電子が原点にいて、もう一つの電子がその距離にいる確率密度( 橙色:$P_{100}^{Z=2}(0,r) $ )」。あと比較対象として、「水素原子基底状態に対する動径確率密度分布($P_{100}^{Z=1}(r) $)」と「ヘリウム原子イオンの基底状態に対する動径確率密度分布($P_{100}^{Z=2}(r) $)」を同時にプロットしたよ。
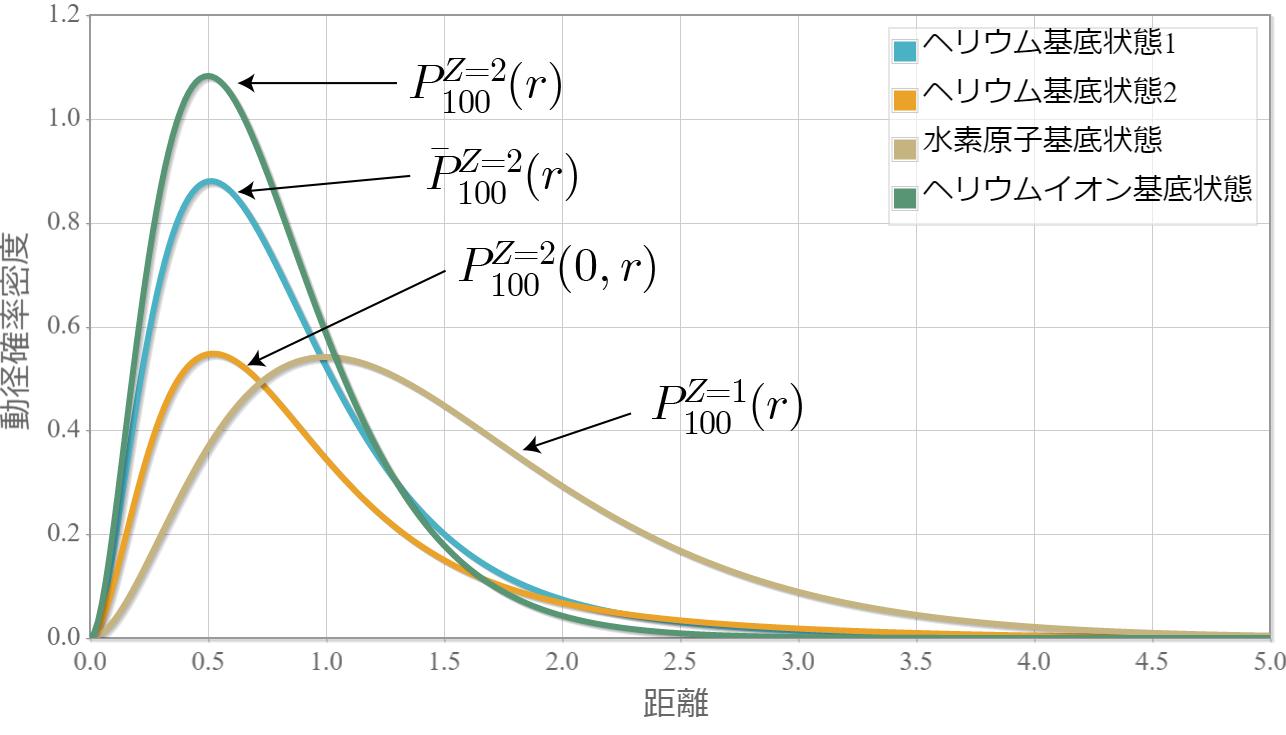
横軸が原点からの距離、縦軸が確率密度だよ。一番強く原子核に束縛されているのが「ヘリウム原子イオンの基底状態」で、反対に最も束縛されていないのが「水素原子の基底状態」だね。つまり、原子核の電荷が $Z=2$ で電子が1個の場合が一番強く束縛されて、$Z=1$ で電子が1個の場合が最も束縛が弱いね。2種類用意したヘリウム原子を比較すると、1個を原点に存在する「橙色:$P_{100}^{Z=2}(0,r) $」は、他方の「青色:$\bar{P}_{100}^{Z=2}(r) $」と比較して、電子間の反発でより遠くに存在することがわかるね。
