水素分子の固有状態の数値計算方法（失敗）

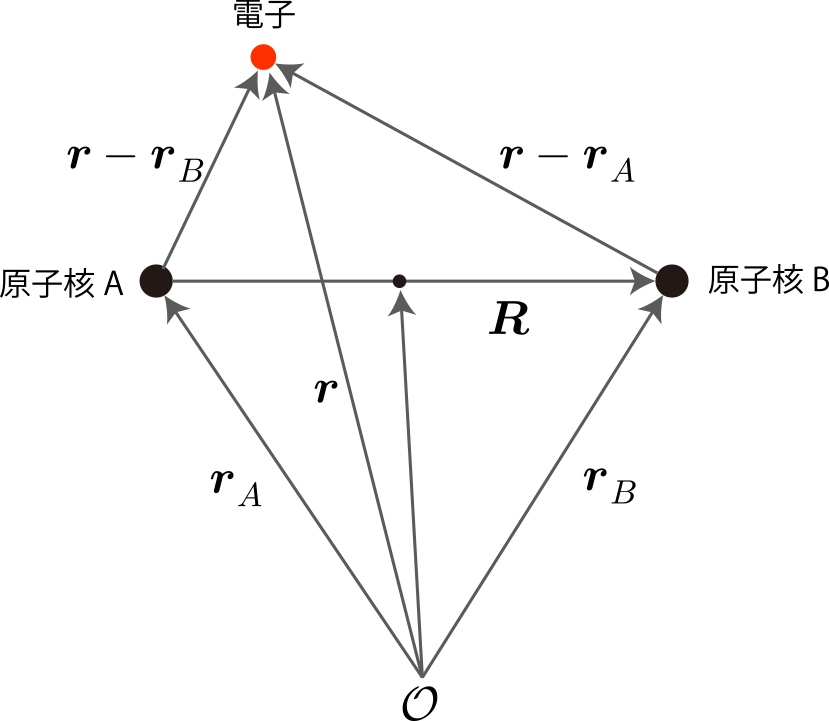
右図で表したような、$Z=1$ の原子核２個の周りを回る電子１個となる水素分子イオンのエネルギー準位を計算するよ。２つの原子核は空間に固定されていると考えると、ハミルトニアンは次のようになるね。

\begin{align}
\hat{H} = -\frac{\hbar^2}{2m_e} \nabla^2 + \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_A|} + \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_B|}
\end{align}

今までと同様に、波動関数をそれぞれの原子を基準とした水素原子の固有状態 $\varphi_{nlm}$ で次のように表すことができると考えるよ。

\begin{align}
\psi(\boldsymbol{r}) = \sum\limits_{nlm} \left[ C^{(A)}_{nlm} \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_A) +C^{(B)}_{nlm} \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_B) \right]
\end{align}

これをシュレディンガー方程式 $\hat{H}\psi(\boldsymbol{r}) = E\psi(\boldsymbol{r})$ に代入すると

\begin{align}
\sum\limits_{nlm} C^{(A)}_{nlm} \left[ E_n + \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_B|} \right] \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_A) &\ +\sum\limits_{nlm} C^{(B)}_{nlm} \left[ E_n + \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_A|} \right] \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_B) \\
&\ = E \sum\limits_{nlm} \left[ C^{(A)}_{nlm} \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_A) +C^{(B)}_{nlm} \varphi_{nlm}(\boldsymbol{r} -\boldsymbol{r}_B) \right]
\end{align}

となるね。ここから係数を計算するための固有値方程式を導入するために、両辺に $\varphi_{nlm}^*(\boldsymbol{r} -\boldsymbol{r}_A)$ と $\varphi_{nlm}^*(\boldsymbol{r} -\boldsymbol{r}_B)$ をそれぞれ掛けて全空間で積分するけれども、その際に「異なる量子数」に対する空間積分が直交してほしいけれども、きっと直交しないね。

両辺に $\varphi_{nlm}^*(\boldsymbol{r} -\boldsymbol{r}_A)$ を掛けて全空間で積分

\begin{align}
C^{(A)}_{n’l’m’} E_{n’} + \frac{e^2}{4\pi \epsilon_0 } \sum\limits_{nlm} C^{(A)}_{nlm} {}_A\!\langle n’,l’,m’| \frac{1}{| \boldsymbol{r} -\boldsymbol{r}_B|} |n,l,m\rangle\!{}_A &\ +\sum\limits_{nlm} C^{(B)}_{nlm} \left[ E_n {}_A\!\langle n’,l’,m’|n,l,m\rangle\!{}_B + {}_A\!\langle n’,l’,m’| \frac{1}{| \boldsymbol{r} -\boldsymbol{r}_A|}|n,l,m\rangle\!{}_B \right] \\
&\ = E \left[ C^{(A)}_{n’l’m’} + \sum\limits_{nlm} C^{(B)}_{nlm} {}_A\!\langle n’,l’,m’|n,l,m\rangle\!{}_B \right]
\end{align}

いつもどおりに固有値方程式の導出を試みたけれども、やっぱり直交しないことがネックとなって、うまくいかないね。もうちょっと工夫してみるね。