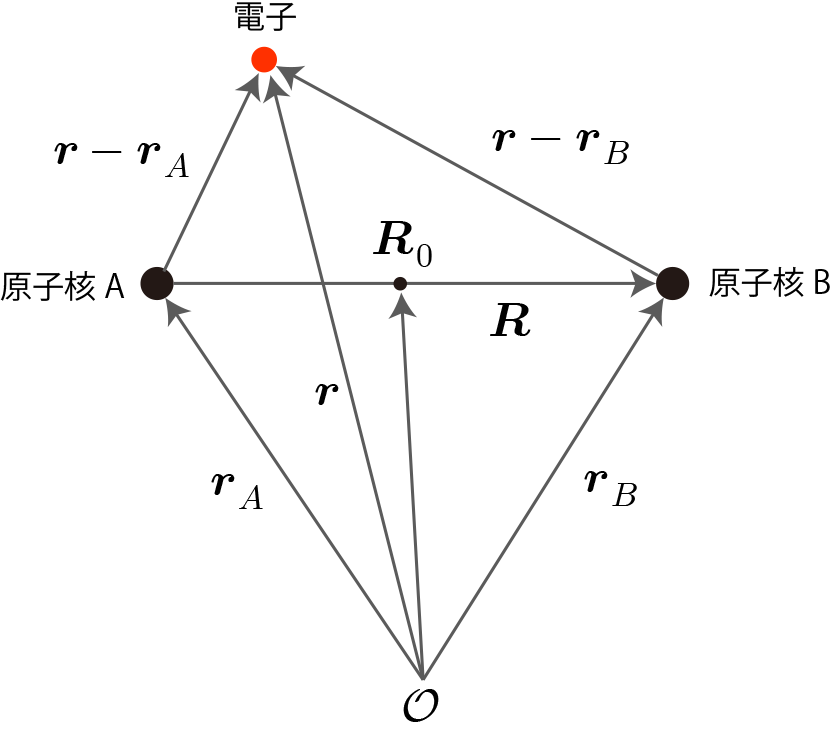
前回、水素分子の固有状態の数値計算方法を示そうとしたけれども、展開する直交関数系を全く考慮していなかったために、異なる量子数で直交しないために固有値方程式を導出することができなかったね。今回は、水素分子イオンを構成する2つの原子核の重心位置( $\boldsymbol{R}_0$ )を基準とした水素様原子($Z=2$)の固有関数系で展開する方法で考えてみるよ。
\begin{align}
\psi(\boldsymbol{r}) = \sum\limits_{nlm} a_{nlm} \varphi_{nlm}^{(Z)}(\boldsymbol{r}-\boldsymbol{R}_0)
\end{align}
この固有関数に合わせて、ハミルトニアンを次のように変形するよ。
\begin{align}
\hat{H} &\ = \left[ -\frac{\hbar^2}{2m_e} \nabla^2 – \frac{Ze^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{R}_0|} \right] + \left[ \frac{Ze^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{R}_0|} – \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_A|} – \frac{e^2}{4\pi \epsilon_0 | \boldsymbol{r} -\boldsymbol{r}_B|} \right] \\\\
&\ = \hat{H}_0^{(Z)} + V(\boldsymbol{r})
\end{align}
このように変形することで、$ \hat{H}_0 \varphi_{nlm}^{(Z)} (\boldsymbol{r}-\boldsymbol{R}_0) = E_n^{(Z)} \varphi_{nlm}^{(Z)} (\boldsymbol{r}-\boldsymbol{R}_0) $ と固有状態となるね。シュレディンガー方程式 $\hat{H} \psi(\boldsymbol{r}) = E \psi(\boldsymbol{r})$ に代入してすると
\begin{align}
\sum\limits_{nlm} a_{nlm} \left[ E_n + V(\boldsymbol{r}) \right] \varphi_{nlm}^{(Z)} (\boldsymbol{r}-\boldsymbol{R}_0) = E \sum\limits_{nlm} a_{nlm} \varphi_{nlm}^{(Z)} (\boldsymbol{r}-\boldsymbol{R}_0)
\end{align}
となるので、いつものとおり、両辺に $ \varphi_{n’l’m’}^{(Z)*}(\boldsymbol{r}-\boldsymbol{R}_0)$ を掛けて全空間で積分すると、
\begin{align}
a_{n’l’m’} E_{n’} + \sum\limits_{nlm} a_{nlm} \langle n’,l’,m’| V(\boldsymbol{r}) | n, l, m \rangle = Ea_{n’l’m’}
\end{align}
となって、最も単純な固有値方程式の形になるね。ちなみに
\begin{align}
\langle n’,l’,m’| V(\boldsymbol{r}) | n, l, m \rangle &\ = \int \varphi_{n’l’m’}^{(Z)*}(\boldsymbol{r}-\boldsymbol{R}_0) V(\boldsymbol{r}) \varphi_{nlm}^{(Z)}(\boldsymbol{r}-\boldsymbol{R}_0) dV\\
\delta_{nn’}\delta_{ll’}\delta_{mm’} &\ = \int \varphi_{n’l’m’}^{(Z)*}(\boldsymbol{r}-\boldsymbol{R}_0) \varphi_{nlm}^{(Z)}(\boldsymbol{r}-\boldsymbol{R}_0) dV
\end{align}
だよ。このポテンシャル項を具体的に計算するために、原子核Aと原子核Bの重心位置を原点($\boldsymbol{R}_0=0 $)、原子核Aを基準とした原子核Bの位置ベクトルを $\boldsymbol{R} = (R,0,0)$ として、改めてポテンシャル項を書き直すと次のようになるね。
\begin{align}
V(\boldsymbol{r}) = -\frac{e^2}{4\pi \epsilon_0} \left[ \frac{1}{|\boldsymbol{r} -\frac{1}{2}\boldsymbol{R}|} + \frac{1}{|\boldsymbol{r} + \frac{1}{2}\boldsymbol{R}|} – \frac{Z}{|\boldsymbol{r}|} \right]
\end{align}
次回は、この計算結果を示すよ。
