【量子コンピュータを作ろう！】（８）２重量子ドットに束縛された電子の固有状態の計算方法（改）

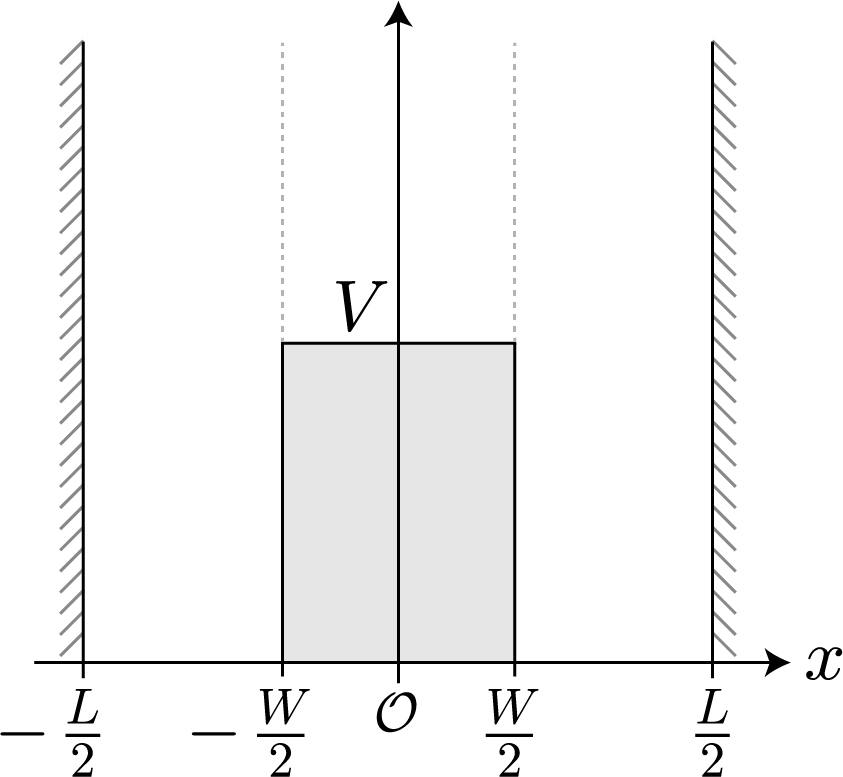
前回、各領域に分けて接続条件から固有状態を計算しようと考えたけれど、よく考えたらこの方法は考え方が間違っているね。特に、特定の壁の高さや幅でしか固有状態が存在しないって言う点は完全に間違いだね。「単一の波数だけで固有状態をなす」という意味では特定の壁の高さや幅でしか固有状態が存在しないというのは正しいけれども、てっきり解析的に固有状態が求まると思い込んでいたことが問題だったね。ということで、これまでと同様に、解を正規直交系で展開して固有値方程式を解く必要がありそうだね。

固有状態の計算方法

１次元井戸型ポテンシャルのハミルトニアンは

\begin{align}
\hat{H} = -\frac{\hbar^2}{2m_e}\, \frac{d^2}{d x^2} + V(x)
\end{align}

で表されるね。$V(x)$ は以下のとおりだよ。

\begin{align}
V(x) = \left\{ \matrix{ \infty & x \leq -\frac{L}{2} \cr 0 & -\frac{L}{2} \leq x\leq -\frac{W}{2} \cr V & -\frac{W}{2} \leq x\leq \frac{W}{2} \cr 0 & \frac{W}{2} \leq x\leq \frac{L}{2} \cr \infty & \frac{L}{2} \leq x} \right.
\end{align}

このハミルトニアンの固有状態 $\bar{\varphi}(x)$ を、真ん中に壁が存在しない場合の固有関数

\begin{align}
\varphi_n(x) = \sqrt{\frac{2}{L}}\sin\left[ k_n \left( x + \frac{L}{2}\right)\right] \ , \ k_n = \frac{\pi(n+1)}{2}
\end{align}

で

\begin{align}
\bar{\varphi}(x) = \sum\limits_{n=0} a_0 \varphi_n(x)
\end{align}

と展開することを考えるよ。この固有関数をシュレーディンガー方程式 $\hat{H} \bar{\varphi}(x) = E\bar{\varphi}(x)$ に代入して、両辺に $\varphi_m(x)^*$ を掛けて全空間で積分するよ。これまでと同様、展開係数 $a_m$ についての連立方程式が導かれるね。

\begin{align}
E_m a_m + \sum\limits_{n=0}\langle m |V(x)| n \rangle a_n = E a_m
\end{align}

ただし、

\begin{align}
\langle m |V(x)| n \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi_m(x)^* V(x) \varphi_n(x) dx
\end{align}

だよ。次回は固有関数を計算してみるよ。