【量子コンピュータを作ろう！】（９）２重量子ドットに束縛された電子の固有状態の計算結果

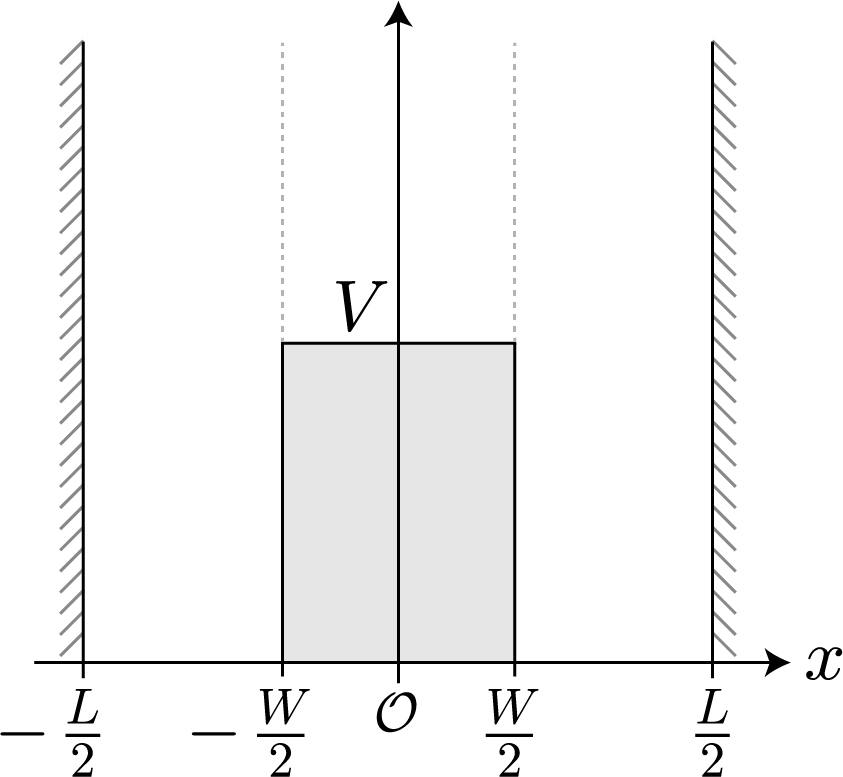
前回導出した２重量子ドットに束縛された電子の固有状態の計算方法を用いて計算した結果を示すよ。具体的なパラメータとして、量子井戸全体のサイズを $L = 10[{\rm nm}]$、真ん中の壁のサイズを $W = 2[{\rm nm}]$ として、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させてみたよ。まずは、固有状態から見てみよう！

固有状態の空間分布

基底状態

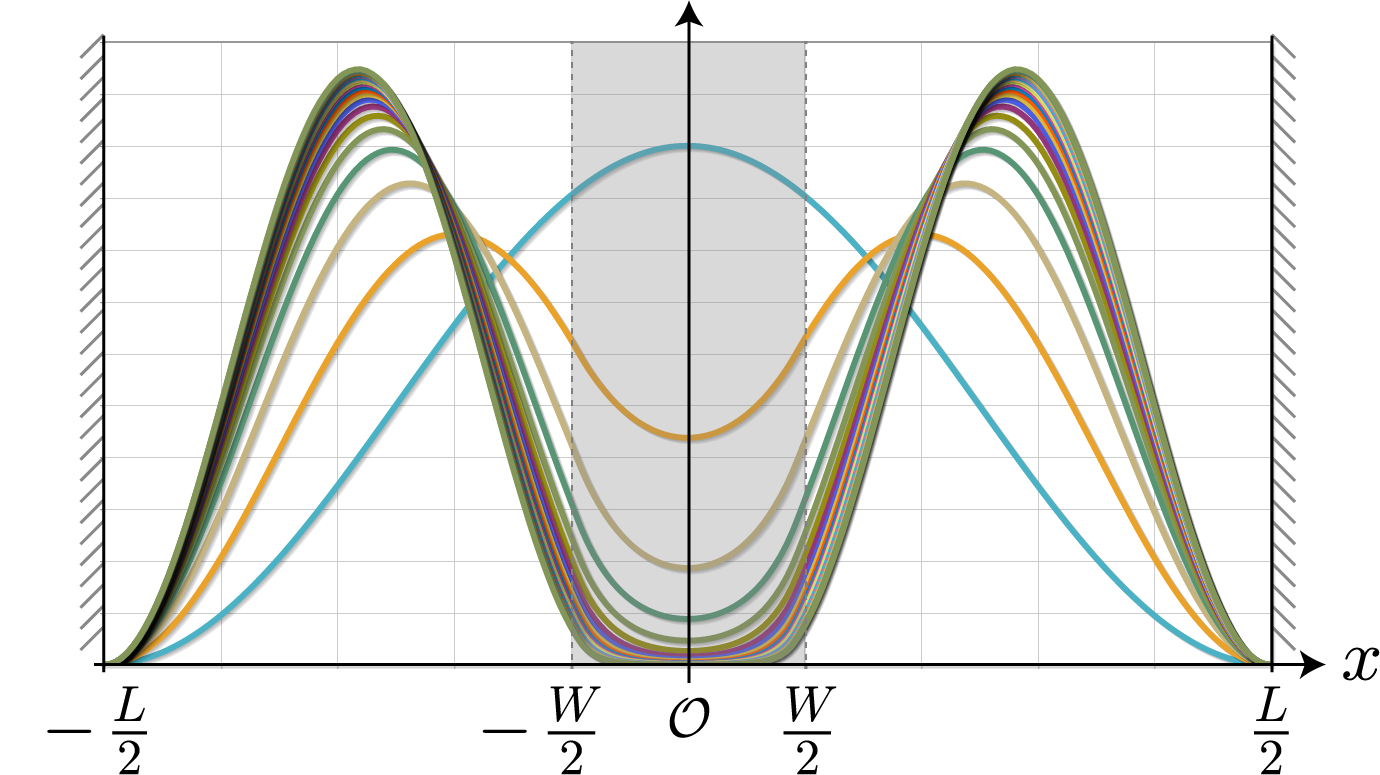
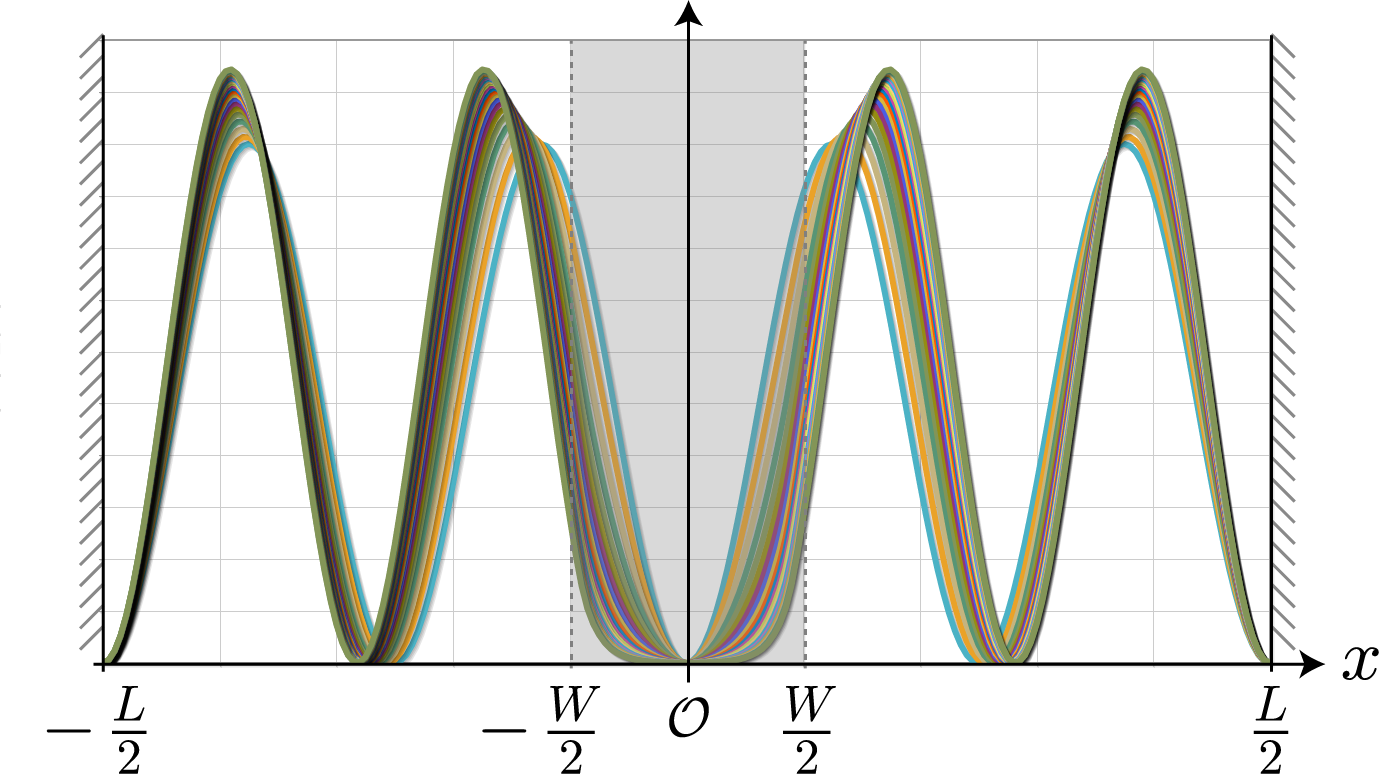
次の図は、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させたときの基底状態の空間分布だよ。壁の高さが高くなるほど電子分布のピークは両サイドの中心に移動していく様子が分かるね。ちなみに、基底状態の固有エネルギーは約 $0.004[{\rm eV}]$ だよ。

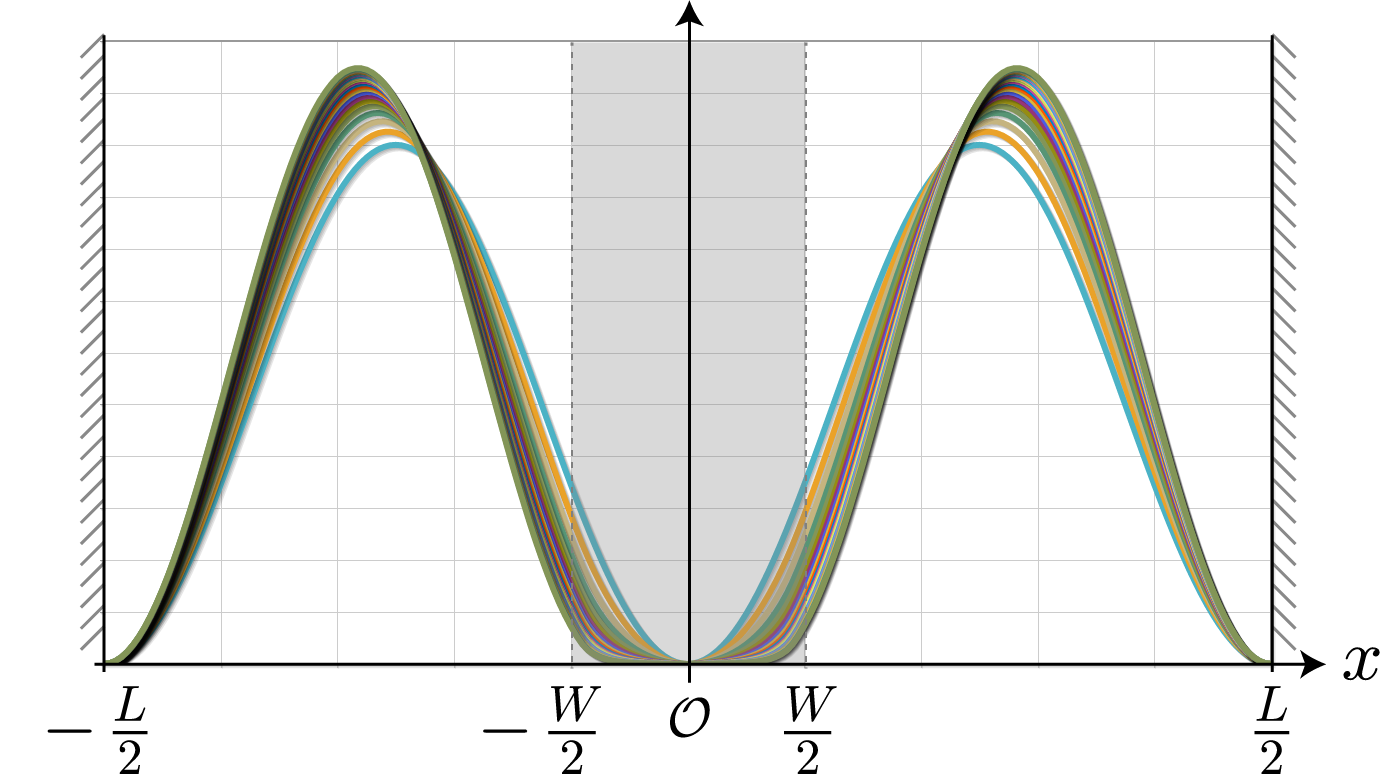
第一励起状態

次の図は、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させたときの第一励起状態の空間分布だよ。壁の高さが高くなるほど電子分布のピークは両サイドの中心に移動していくけれども、もともと第一励起状態は sin関数的なので変化は小さいね。ちなみに、基底状態の固有エネルギーは $0.015[{\rm eV}]$ 程度だよ。

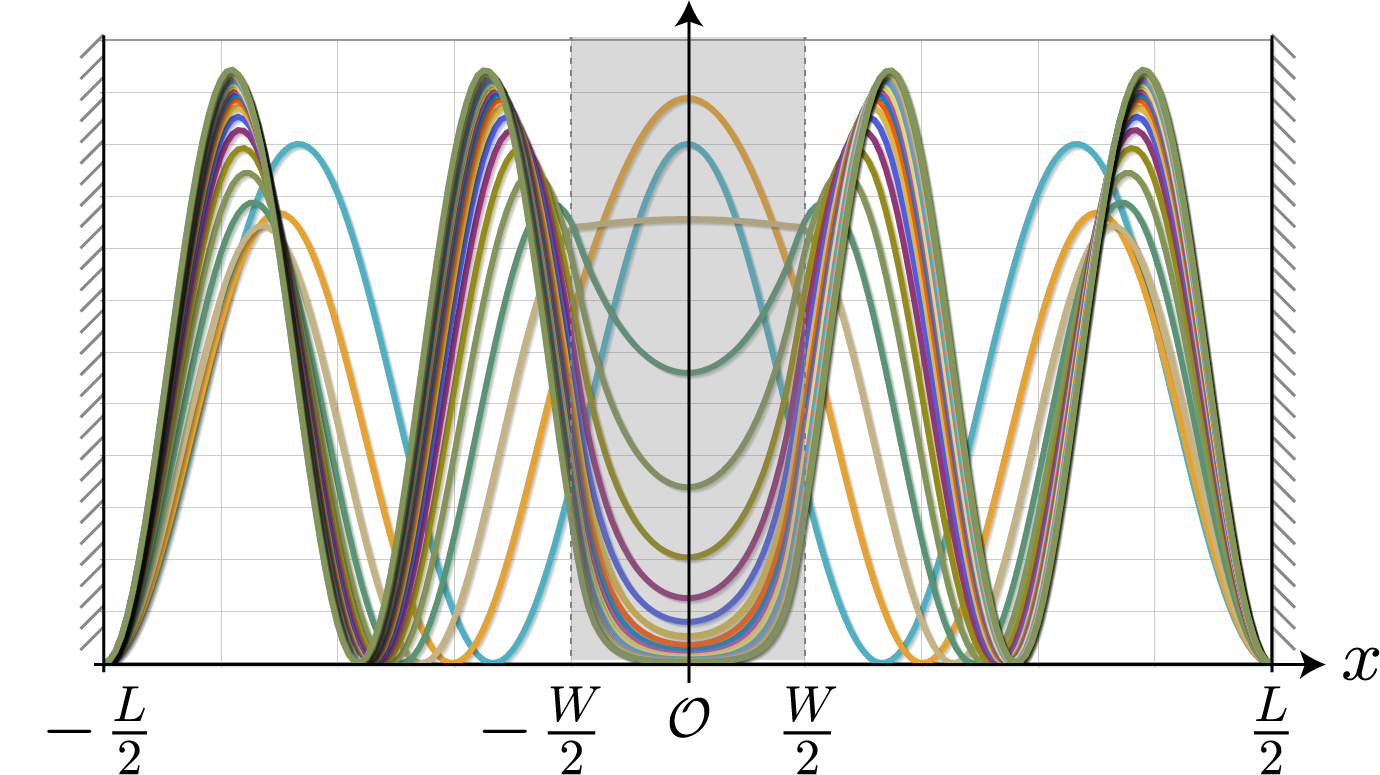
第二励起状態

次の図は、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させたときの第二励起状態の空間分布だよ。基底状態と同様、壁の高さが高くなるほど電子分布のピークは両サイドの中心に移動していく様子が分かるね。ちなみに、基底状態の固有エネルギーは約 $0.034[{\rm eV}]$ だよ。

第三励起状態

次の図は、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させたときの第三励起状態の空間分布だよ。第一励起状態と同様、壁の高さが高くなるほど電子分布のピークは両サイドの中心に移動していくけれども、もともと第三励起状態は sin関数的なので変化は小さいね。ちなみに、基底状態の固有エネルギーは約 $0.060[{\rm eV}]$ だよ。

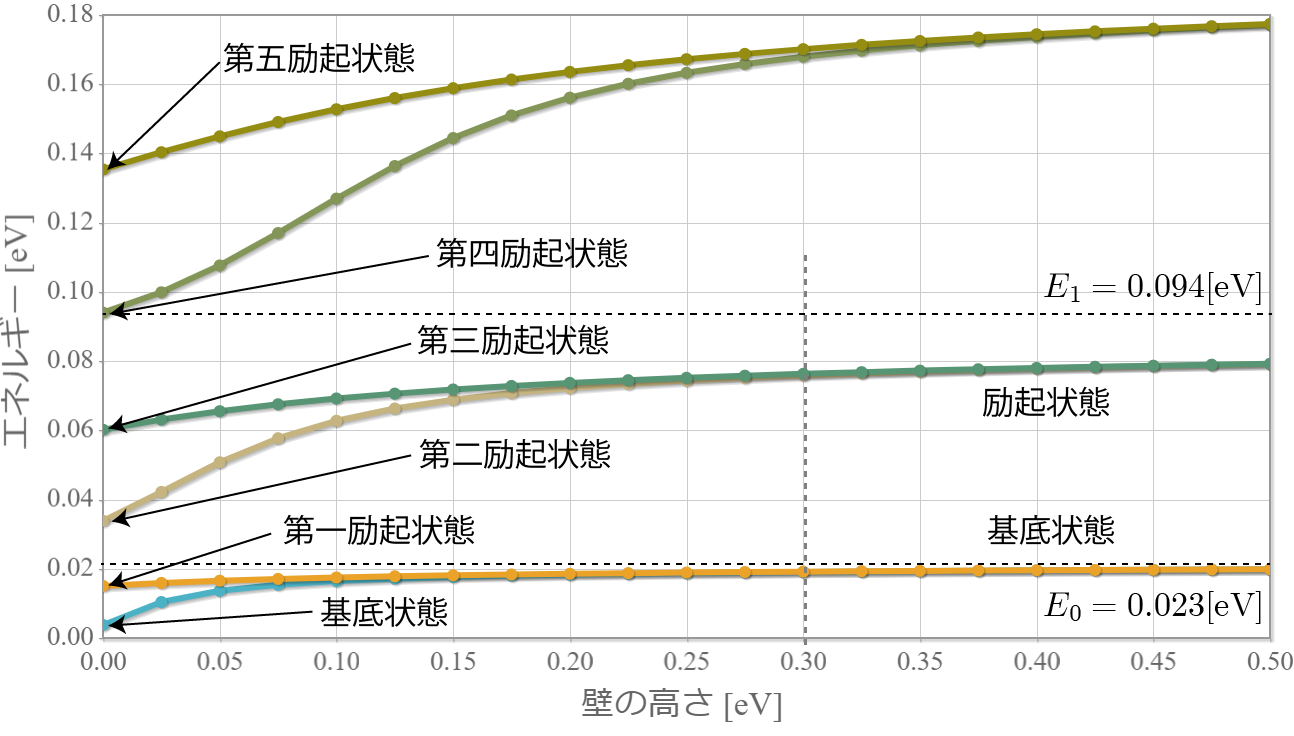
エネルギー準位の壁の高さ依存性

先の固有状態からわかるとおり、壁の高さを高くするほど基底状態と第一励起状態、また第二励起状態と第三励起状態が一致していくね。これは、壁が高くなるほど、2つの領域はそれぞれ孤立していくことに起因するね。次の図は下から６つのエネルギー準位の壁の高さ依存性だけれども、このことはグラフにも現れているね。おおよそ壁の高さが $0.3[{\rm eV}]$ で基底状態と第一励起状態、第二励起状態と第三励起状態の固有エネルギーが概ね一致しているね。ちなみに、横の点線 $E_0=0.023[{\rm eV}]$ と $E_1=0.094[{\rm eV}]$ は、壁の高さが無限大とした場合の固有エネルギーの値だよ。

次回はさらに静電場を加えてみるよ。