物理シミュレーションが趣味なシミュ君のページ
この前導出した水素原子の外場による光電効果の計算方法に基づいて計算した結果を示すよ。入射した電磁場の波長は $ \lambda = 10\, a_B $ （ $a_B$ はボーア半径、 $ E= E = 2343[{\rm eV}] $）。長さ $L$ の箱内で定義される平面波で展開したせいか、飛び出したはずの電子が、外場の影響を受けてまた基底状態に戻るっていう結果になってしまったよ。考えてみれば、これはラビ振動と全く同じ物理的な状況だね。
\[\begin{align}
i
\end{align}\tag{10}\]
この前、水素原子の外場による光電効果の数値計算方法を導出したけれども、この表式では、放出した電子は外場の影響をうけてしまって、放出方向がわからなくなってしまうね。今回はもう少し物理的な描像がわかりやすくなるような表式の導入を行うよ。波動関数を初期状態とする水素原子の基底状態 $\varphi_{100}$ と飛び出した電子の平面波を表す項の２つで
\begin{align}
\psi(\boldsymbol{r}, t) = a(t) \varphi_{100}(\boldsymbol{r}) + \sum\limits_{\boldsymbol{n}}’b_{\boldsymbol{n}}(t) \frac{1}{\sqrt{V}} \, e^{i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}
と表すとするよ。ただし、$ \boldsymbol{k} = \frac{2\pi}{L}(n_x, n_y, n_z) $ で、$L$ は空間サイズで $V =L^3$、 $\boldsymbol{n} = (n_x, n_y, n_z)$ は整数だよ。注意する点は、上記の和はすべての $\boldsymbol{n}$ で取らずに、基底状態 $\varphi_{100}(\boldsymbol{\boldsymbol{r}})$ の波数成分
\begin{align}
\varphi_{100}(\boldsymbol{\boldsymbol{k}}) = \frac{1}{\sqrt{V}} \int \varphi_{100}(\boldsymbol{r})e^{-i\boldsymbol{k}\cdot\boldsymbol{r}} dV
\end{align}
を含まない $\boldsymbol{n}$ に限って和を取るという制限をつけるよ。そうすることで、
\begin{align}
\int \varphi_{100}(\boldsymbol{r})e^{-i\boldsymbol{k}\cdot\boldsymbol{r}} dV = 0
\end{align}
というふうに、基底状態と平面波が直交すると考えることができるからね。これをハミルトニアン
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}} =\hat{H}_0 + \frac{e}{im_e}
\,\boldsymbol{A}\cdot\nabla
\end{align}
とするシュレーディンガー方程式
\begin{align}
i\hbar\frac{\partial}{\partial t} \psi(\boldsymbol{r}, t) = \hat{H} \psi(\boldsymbol{r}, t)
\end{align}
に代入した
\begin{align}
i\hbar \left[\varphi_{100}(\boldsymbol{r}) \frac{d a(t)}{d t} + \sum\limits_{\boldsymbol{n}}’ \frac{1}{\sqrt{V}} \, e^{i\boldsymbol{k}\cdot\boldsymbol{r}} \frac{d b_{\boldsymbol{n}}(t)}{dt} \right] = a(t) \left(E_{100} +\frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}}\right)\varphi_{100}(\boldsymbol{r}) + \left( \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}} \right) \sum\limits_{\boldsymbol{n}}’b_{\boldsymbol{n}}(t) \frac{1}{\sqrt{V}} \, e^{i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}
から出発して、展開係数 $a(t)$ と $b_{\boldsymbol{n}}(t)$ の時間発展の表式を導出するよ。ちなみに、外場は波数ベクトル $\boldsymbol{K}$、角振動数 $\omega$ のベクトルポテンシャル
\begin{align}
\boldsymbol{A} = \boldsymbol{A}_0 \left[ e^{i\boldsymbol{K}\cdot\boldsymbol{r} – i\omega t} + e^{-i\boldsymbol{K}\cdot\boldsymbol{r} + i\omega t}\right]
\end{align}
で表すよ。ただし、分散関係は電磁波なので光速 $c$ を用いて $\omega = cK$ となるよ。
先の基底状態と平面波の直交性と、$\hat{\boldsymbol{p}}/m_e = [ \hat{H}_0,\boldsymbol{r}]/i\hbar $を考慮して、両辺に $\varphi_{100}^*(\boldsymbol{r})$ を掛けて全空間で積分すると次のようになるよ。
\begin{align}
i\hbar \frac{d a(t)}{d t} = E_{100}a(t) + \frac{\hbar e}{im_e}\sum\limits_{\boldsymbol{n}}’b_{\boldsymbol{n}}(t)\frac{1}{\sqrt{V}} \int \varphi_{100}^*(\boldsymbol{r}) \boldsymbol{A}\cdot \nabla e^{i\boldsymbol{k}\cdot\boldsymbol{r}} dV
\end{align}
第２項目の積分は
\begin{align}
\frac{1}{\sqrt{V}} \int \varphi_{100}^*(\boldsymbol{r}) \boldsymbol{A}\cdot \nabla e^{i\boldsymbol{k}\cdot\boldsymbol{r}} dV &\ = i\boldsymbol{A}_0\cdot\boldsymbol{k} \left[ \frac{1}{\sqrt{V}} \int \varphi_{100}^*(\boldsymbol{r}) e^{i(\boldsymbol{k}+\boldsymbol{K})\cdot\boldsymbol{r}} dV e^{-i\omega t } + \frac{1}{\sqrt{V}} \int \varphi_{100}^*(\boldsymbol{r}) e^{i(\boldsymbol{k}-\boldsymbol{K})\cdot\boldsymbol{r}} dV e^{i\omega t } \right] \\
&\ = i\boldsymbol{A}_0\cdot\boldsymbol{k} \left[ \varphi_{100}^*(\boldsymbol{k}+\boldsymbol{K})e^{-i\omega t } +\varphi_{100}^*(\boldsymbol{k} – \boldsymbol{K})e^{i\omega t } \right]
\end{align}
と表すことができるので、これを元の式に代入した
\begin{align}
i\hbar \frac{d a(t)}{d t} = E_{100}a(t) + \frac{\hbar e}{m_e}\sum\limits_{\boldsymbol{n}}’ \boldsymbol{A}_0\cdot\boldsymbol{k} \left[ \varphi_{100}^*(\boldsymbol{k}+\boldsymbol{K})e^{-i\omega t } +\varphi_{100}^*(\boldsymbol{k} – \boldsymbol{K})e^{i\omega t } \right]b_{\boldsymbol{n}}(t)
\end{align}
が、係数 $a(t)$ に対する常微分方程式だね。この式はひとまず置いておくよ。
今度は、平面波の展開係数に関する表式を得るために、両辺に $\frac{1}{\sqrt{V}} e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}}$ を掛けて全空間で積分するよ。基底状態と平面波の直交性を考慮すると次のようになるよ。
\begin{align}
i\hbar \frac{d b_{\boldsymbol{n}’}(t)}{d t} = a(t) \frac{\hbar e}{m_e}\frac{1}{\sqrt{V}} \int e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}} \boldsymbol{A}\cdot \hat{\boldsymbol{p}} \varphi_{100}(\boldsymbol{r}) dV + \sum\limits_{\boldsymbol{n}}’b_{\boldsymbol{n}}(t)\, \frac{1}{V}\int e^{-i\boldsymbol{k}’\cdot\boldsymbol{r} } \left( \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}} \right) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} dV
\end{align}
この内、まず右辺第２目は、平面波同士の相互作用を表しているね。もう少し具体的に言うと、$H_0$ 因子は原子核の存在による変化、$\boldsymbol{A}\cdot \hat{\boldsymbol{p}}$ 因子は外場による変化を表しているね。今回は、光電効果に着目するので、電離したあとの電子は、原子核や外場の影響を受けずににまっすぐ進んでと想定したいので、この項を無視するね。
次に、第１項目だけれども、この積分は先に導出した積分と非常によく似ているね。部分積分を行って整理すると
\begin{align}
\frac{1}{\sqrt{V}} \int e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}\varphi_{100}(\boldsymbol{r}) dV
&\ = i \boldsymbol{A}_0\cdot \boldsymbol{k}’\left[ \frac{1}{\sqrt{V}} \int \varphi_{100}(\boldsymbol{r}) e^{-i(\boldsymbol{k}’-\boldsymbol{K})\cdot\boldsymbol{r}} dV e^{-i\omega t } + \frac{1}{\sqrt{V}} \int \varphi_{100}(\boldsymbol{r})e^{-i(\boldsymbol{k}’+\boldsymbol{K})\cdot\boldsymbol{r}} dV e^{i\omega t } \right]\\
&\ = i\boldsymbol{A}_0\cdot\boldsymbol{k}’ \left[ \varphi_{100}(\boldsymbol{k}’-\boldsymbol{K})e^{-i\omega t }
+\varphi_{100}(\boldsymbol{k}’ + \boldsymbol{K})e^{i\omega t } \right]
\end{align}
と表すことができるので、これを元の式に代入した
\begin{align}
i\hbar \frac{d b_{\boldsymbol{n}’}(t)}{d t} = \frac{\hbar e}{m_e} \boldsymbol{A}_0\cdot\boldsymbol{k}’ \left[ \varphi_{100}(\boldsymbol{k}’-\boldsymbol{K})e^{-i\omega t }
+\varphi_{100}(\boldsymbol{k}’ + \boldsymbol{K})e^{i\omega t } \right]a(t)
\end{align}
以上をまとめると、基底状態の係数 $a(t)$ と平面波の展開係数 $b_{\boldsymbol{n}}(t)$ は連立常微分方程式
\begin{align}
i\hbar \frac{d a(t)}{d t} &\ = E_{100}a(t) + \frac{\hbar e}{m_e}\sum\limits_{\boldsymbol{n}}’
\boldsymbol{A}_0\cdot\boldsymbol{k} \left[ \varphi_{100}^*(\boldsymbol{k}+\boldsymbol{K})e^{-i\omega t }
+\varphi_{100}^*(\boldsymbol{k} – \boldsymbol{K})e^{i\omega t } \right]b_{\boldsymbol{n}}(t)\\
i\hbar \frac{d b_{\boldsymbol{n}’}(t)}{d t} &\ = \frac{\hbar e}{m_e} \boldsymbol{A}_0\cdot\boldsymbol{k}’ \left[ \varphi_{100}(\boldsymbol{k}’-\boldsymbol{K})e^{-i\omega t }+\varphi_{100}(\boldsymbol{k}’ + \boldsymbol{K})e^{i\omega t } \right]a(t)
\end{align}
に従って時間発展するね。基底状態のフーリエ変換はすでに計算しているのでこれを利用して、初期条件を $a(0)=1$、$b_{\boldsymbol{n}}(0) =0$ として、時刻が大きくなるに連れて、$|a(t)|^2$ が小さくなって行くに従って $b_{\boldsymbol{n}}(t)$ が大きくなることが想定されるね。そのときの $\boldsymbol{n}$ の分布が電子が飛び出していく方向を表すよ。次回は実際に計算してみるよ。
水素原子の電子に直線偏光の電磁波（古典）を入射したときの状態遷移は以前解説したね。今回は、入射した電磁波の振動数を高めることで生じる「光電効果」（束縛状態の電子が外場によって非束縛状態へ遷移する効果）をシミュレーションするのに必要な表式を導出するよ。スピンと外場の２次の項を無視したハミルトニアンは、
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \hat{\boldsymbol{p}} = -\frac{\hbar^2}{2m_e}\nabla^2 + V(r) + \frac{e}{im_e} \,\boldsymbol{A}\cdot\nabla
\end{align}
となるね。このハミルトニアンを用いたシュレディンガー方程式
\begin{align}
i\hbar\frac{\partial}{\partial t} \psi(\boldsymbol{r}, t) = \hat{H} \psi(\boldsymbol{r}, t)
\end{align}
だね。ここから出発するよ。今回は、水素原子核に束縛された状態からとき放たれた状態も考慮するため、波動関数は波数空間で展開した
\begin{align}
\psi(\boldsymbol{r}, t) = \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z} a_{n_xn_yn_z}(t)\, e^{i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}
で表すよ。ただし、$ \boldsymbol{k} = \frac{2\pi}{L}(n_x, n_y, n_z) $ で、$L$ は空間サイズで $V =L^3$、 $n_x, n_y, n_z$ は整数だよ。これをシュレディンガー方程式に代入して、両辺に $\frac{1}{\sqrt{V}}e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}}$ を掛けて、全空間で積分すると
\begin{align}
i\hbar\frac{d a_{n_x’n_y’n_z’}(t)}{d t} = \left[ \frac{\hbar^2k’^2}{2m_e} + \frac{e}{m_e} \,\boldsymbol{A}\cdot \boldsymbol{k}’ \right] a_{n_x’n_y’n_z’}(t) + \frac{1}{V}\sum\limits_{n_x, n_y, n_z} \left[ \int e^{-i\boldsymbol{k}’\cdot\boldsymbol{r}} V(r) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} dV \right] a_{n_xn_yn_z}(t)
\end{align}
となるね。さらにポテンシャル項もついでに
\begin{align}
V(r) = \frac{1}{\sqrt{V}}\sum\limits_{n”_x, n”_y, n”_z} v_{n”_xn”_yn”_z}\, e^{i\boldsymbol{k}”\cdot\boldsymbol{r}}
\end{align}
と展開して代入すると、空間積分を実行することができて、次のような形になるね。
\begin{align}
i\hbar\frac{d a_{n_x’n_y’n_z’}(t)}{d t} = \left[ \frac{\hbar^2k’^2}{2m_e} + \frac{e}{im_e} \,\boldsymbol{A}\cdot \boldsymbol{k}’ \right] a_{n_x’n_y’n_z’}(t) + \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z}\,v_{n_x’-n_x,n_y’-n_y,n_z’-n_z} a_{n_xn_yn_z}(t)
\end{align}
さらに、クーロンポテンシャル $ V(r) = -e^2/4\pi\epsilon r$のように $1/r$ の場合には、展開係数 $ v_{n”_xn”_yn”_z} $ は解析的に導出することができて、
\begin{align}
v_{n”_xn”_yn”_z} = \frac{1}{\sqrt{V}} \int V(r)e^{-i\boldsymbol{k}”\cdot\boldsymbol{r}} dV = -\frac{e^2}{4\pi\epsilon_0} \, \frac{1}{k”^2}
\end{align}
で与えられるので、最終的には
\begin{align}
i\hbar\frac{d a_{n_x’n_y’n_z’}(t)}{d t} = \left[ \frac{\hbar^2k’^2}{2m_e} + \frac{e}{im_e} \,\boldsymbol{A}\cdot \boldsymbol{k}’ \right] a_{n_x’n_y’n_z’}(t) -\frac{e^2}{4\pi\epsilon_0}\, \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z}\,\frac{1}{k_{n_x’-n_x,n_y’-n_y,n_z’-n_z}^2 }a_{n_xn_yn_z}(t)
\end{align}
となるね。これで、$a_{n_xn_yn_z}$ に関する連立常微分方程式になるね。あとは、外場を与えるベクトルポテンシャル $\boldsymbol{A}$ を計算対象の系に合わせて設定して、ルンゲ・クッタ法を用いて時間発展を計算することができるね。ちなみに、$a_{n_xn_yn_z}$ の初期状態は、
\begin{align}
a_{n_xn_yn_z}(0) = \frac{1}{\sqrt{V}}\sum\limits_{n_x, n_y, n_z} \psi(\boldsymbol{r}, 0) \, e^{-i\boldsymbol{k}\cdot\boldsymbol{r}}
\end{align}
で計算することができるので、例えば、$\psi(\boldsymbol{r}, 0) = \varphi_{100}$ と与えることで、初期状態を基底状態とした場合の計算を行うことができるよ。次回は結果を示すよ。
あとで、電磁波（古典）による「光電効果」（束縛状態の電子が外場によって非束縛状態へ遷移する効果）をシミュレーションしたいので、その準備として、水素原子に束縛された固有状態のフーリエ変換を数値的に調べておくよ。$ \boldsymbol{k} = \frac{2\pi}{L}(n_x, n_y, n_z) $ で、$L$ は空間サイズで $V =L^3$、 $n_x, n_y, n_z$ は整数として、固有状態の波数成分 $\varphi_{nlm}( \boldsymbol{k} )$ は、
\begin{align}
\varphi_{nlm}( \boldsymbol{k} ) = \frac{1}{\sqrt{V}} \int \varphi_{nlm}( \boldsymbol{r} ) e^{-i \boldsymbol{k} \cdot \boldsymbol{r} }dV
\end{align}
で表すことができるね。とりあえず、基底状態 $\varphi_{100}( \boldsymbol{k} ) $ の波数空間分布を示すよ（ $\varphi_{100}( \boldsymbol{k} ) $ の $kx-ky$ 平面上の値を、大きさは不透明度、位相は色で表しているよ）。
前回解説した水素原子に静電場を急激に加えたときの緩和時間シミュレーションの結果を示すよ。次の図は初期状態として $\varphi_{200}$ 100%の状態に $ E_z = 10^{9}[\rm{V/m}]$ の静電場を急に加えたときの $\varphi_{200}$ と $\varphi_{210}$ の存在確率の時間経過だよ。$\varphi_{200}$ 100%の状態と $\varphi_{210}$ 100%の状態が一定の周期で交互に現れるね。
$\varphi_{200}$ と $\varphi_{210}$ は静電場中ではエネルギーが高い一方で、その50%づつの混合状態が一番エネルギーが低いのだよね。つまり、下の図で示したとおり、エネルギーの高い初期状態 $\varphi_{200}$ 100% からスタートして、エネルギー低い方に状態が変化して行くけれども、一番低いところで止まらずに反対の $\varphi_{210}$ 100% の状態まで変化していっているね。もし、エネルギーが散逸するメカニズムがあれば、最低エネルギーに落ち着くよね。きっと。
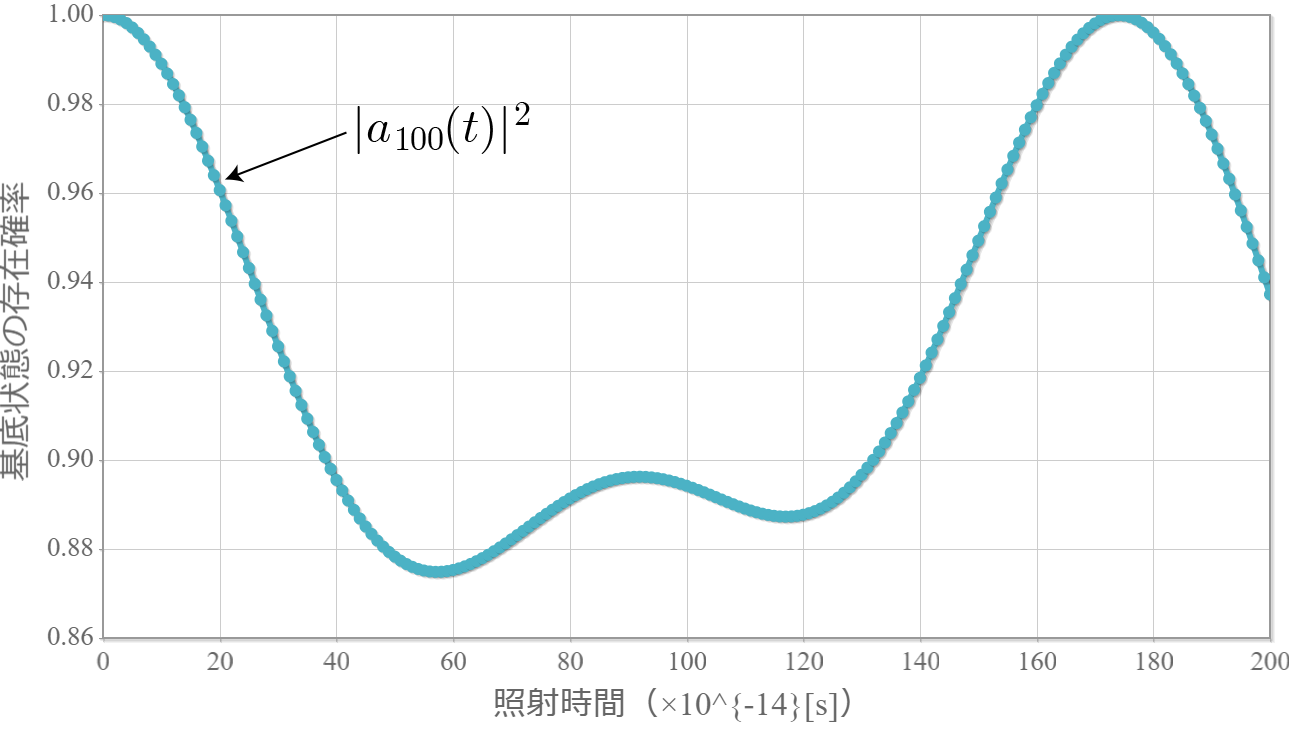
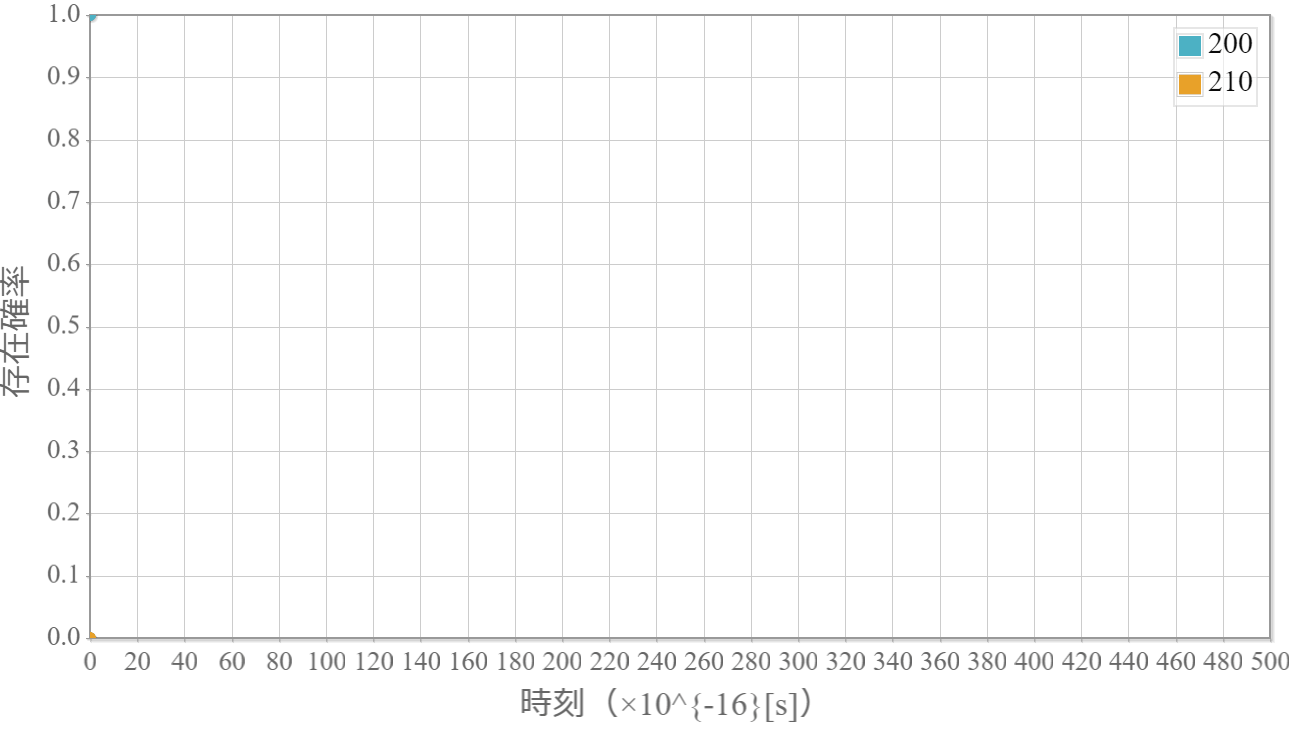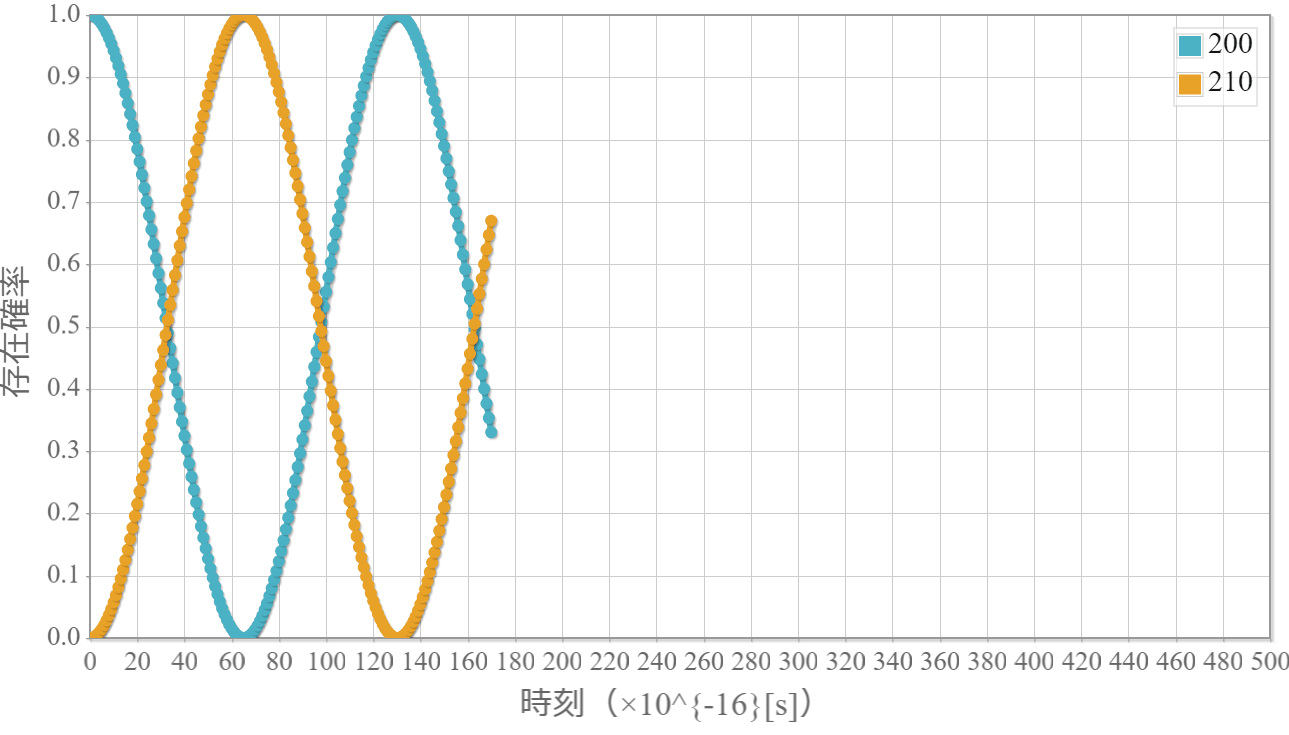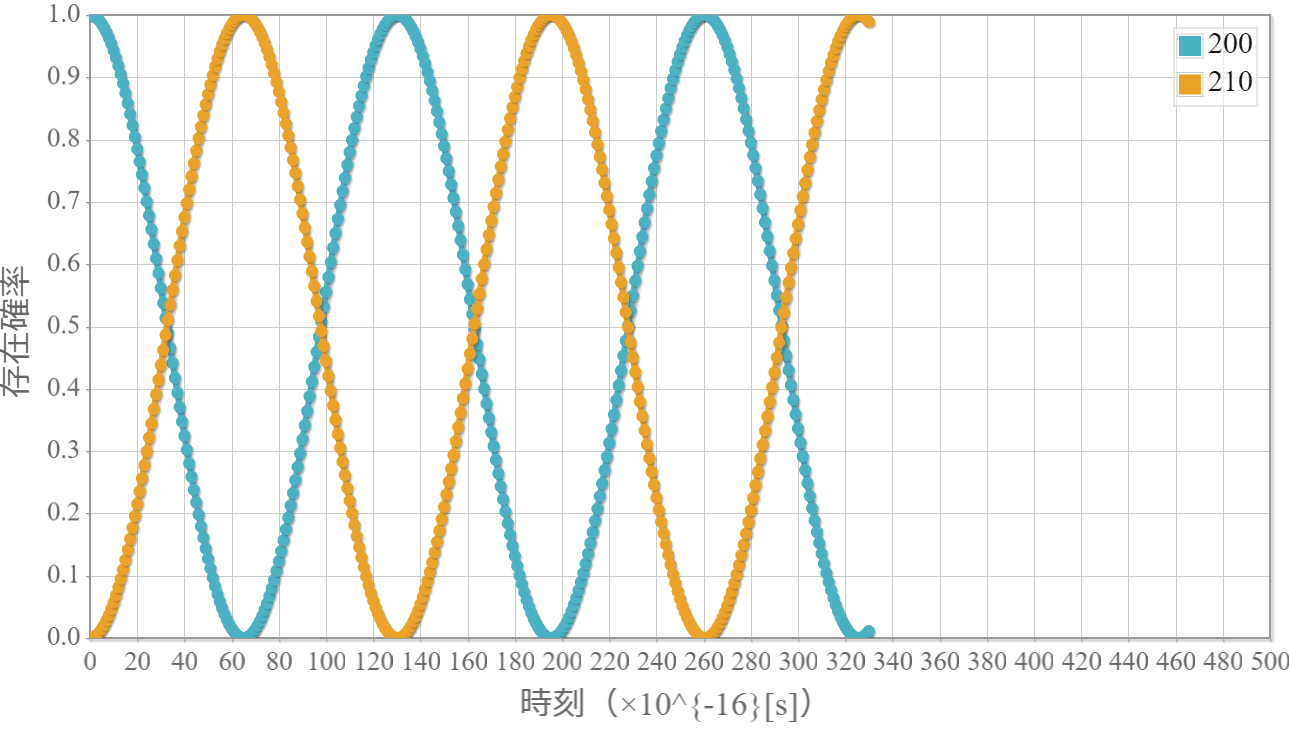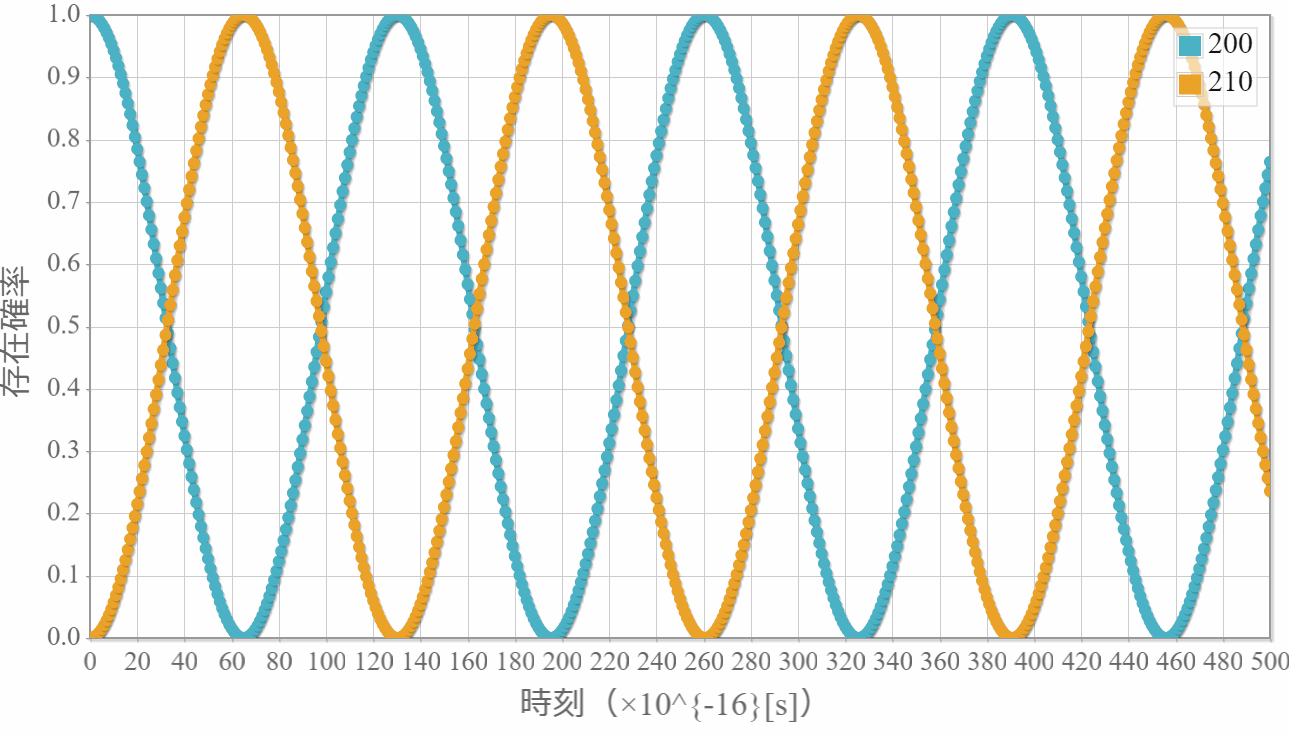
任意の電磁場中を運動する電子のハミルトニアンは「静磁場が加わる場合のハミルトニアンを復習しよう！」で示したとおりだね。ベクトルポテンシャルを $\boldsymbol{A}$、スカラーポテンシャルを $\phi$ とした場合、
\begin{align}
\hat{H} = \frac{1}{2m_e} (\hat{\boldsymbol{p}} + e \boldsymbol{A})^2 -e \phi
\end{align}
となるね。水素原子に束縛された電子を考えると、クーロンゲージを採用して
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \boldsymbol{p} + \frac{e^2 \boldsymbol{A}^2}{2m_e}
\end{align}
となるね。$\hat{H}_0$ は外場が無い場合の水素原子に束縛された電子のハミルトニアン
\begin{align}
\hat{H}_0 = \frac{\hat{\boldsymbol{p}}^2}{2m_e} – \frac{e^2}{ 4\pi\epsilon_0} \, \frac{1}{r}
\end{align}
だよ。電磁波の場合には、このベクトルポテンシャル $\boldsymbol{A}(t)$ が時間に依存するんだね。さらに、スピンも考慮するならば、スピンのゼーマン項を加えて
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{m_e}\,\boldsymbol{A}\cdot \boldsymbol{p} + \frac{e}{m_e} \hat{\boldsymbol{S}}\cdot \boldsymbol{B} + \frac{e^2 \boldsymbol{A}^2}{2m_e}
\end{align}
だね。今回、電磁波の進行方向をx軸として、磁場成分をy軸、電場成分をz軸となるように、ベクトルポテンシャルを
\begin{align}
\boldsymbol{A} = \left(0, 0, A_0 \cos(kx-\omega t) \right)
\end{align}
と与えると、電場と磁場は次のようになるね。
\begin{align}
\boldsymbol{E} &\ = -\frac{\partial \boldsymbol{A}}{\partial t} =\left(0, 0, – \omega A_0 \sin(kx-\omega t) \right)\\
\boldsymbol{B} &\ = \nabla \times \boldsymbol{A} =\left(0, k A_0 \sin(kx-\omega t), 0 \right)
\end{align}
電子の状態遷移を議論するには、時間に依存したシュレディンガー方程式
\begin{align}
i\hbar\frac{\partial}{\partial t} \psi(\boldsymbol{r}, t) = \hat{H} \psi(\boldsymbol{r}, t)
\end{align}
を解けばいいんだね。まずは波動関数 $\psi(\boldsymbol{r}, t) $ を外場無し固有状態で
\begin{align}
\psi(\boldsymbol{r}, t) = \sum\limits_{n, l, m, s_z} a_{nlms_z}(t)\, \varphi_{nlms_z}
\end{align}
のように展開して、展開係数が時間に依存すると考えることができるね。次に、$\hat{H} = \hat{H}_0 + \hat{V}(t)$ とおいてこれをシュレディンガー方程式に代入すると
\begin{align}
\sum\limits_{n, l, m, s_z}i\hbar\frac{d a_{nlms_z}(t)}{d t} \, \varphi_{nlms_z} = \sum\limits_{n, l, m, s_z}\left[E_n + \hat{V}(t)\right] a_{nlms_z}(t)\, \varphi_{nlms_z}
\end{align}
となるね。両辺に $\varphi_{n’l’m’s_z’}^*$ を掛けて全空間で積分すると展開係数に関する連立常微分方程式が得られるね。
\begin{align}
i\hbar\frac{d a_{n’l’m’s_z’}(t)}{d t} = E_{n’}a_{n’l’m’s_z’}(t) + \sum\limits_{n, l, m, s_z} a_{nlms_z}(t) \int \varphi_{n’l’m’s_z’}^* \hat{V}(t)\varphi_{nlms_z} dV
\end{align}
この $\hat{V}(t)$ に電磁波との相互作用を与えるわけだね。$\hat{\boldsymbol{p}}/m_e = -i [\hat{H}_0,\boldsymbol{r} ]/\hbar$ を考慮して、$\hat{V}(t)$ の空間積分の項を見てみよう。
\begin{align}
\int \varphi_{n’l’m’s_z’}^* \hat{V}(t)\varphi_{nlms_z} dV &\ = \int \varphi_{n’l’m’s_z’}^* \left[
-i\frac{e}{\hbar} [\hat{H}_0,\boldsymbol{r} ]\cdot\boldsymbol{A} + \frac{e }{m_e} \hat{S}_yB_y + \frac{e^2 A_0^2}{2m_e}\, \cos^2(kx-\omega t) \right] \varphi_{nlms_z} dV \\
&\ = \int \varphi_{n’l’m’s_z’}^* \left[
-ie \frac{ E_{n’} – E_n }{\hbar}\, z A_0 \cos(kx-\omega t) + \frac{ek\hbar A_0 s_z}{m_e} \,\sin(kx-\omega t) + \frac{e^2 A_0^2}{2m_e}\, \cos^2(kx-\omega t) \right] \varphi_{nlms_z} dV \\
&\ = -\frac{i A_0e}{2} e^{-i\omega t}\int \varphi_{n’l’m’s_z’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z + \frac{k\hbar s_z}{m_e} \right] e^{ikx} \varphi_{nlms_z} dV\\
&\ \ \ \ \ -\frac{i A_0e}{2} e^{i\omega t}\int \varphi_{n’l’m’s_z’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z – \frac{ k\hbar s_z}{m_e} \right] e^{-ikx} \varphi_{nlms_z} dV\\
&\ \ \ \ \ + \frac{e^2 A_0^2}{8m_e} \left[ 1 + e^{-2i\omega t} \int \varphi_{n’l’m’s_z’}^* e^{2ikx} \varphi_{nlms_z} dV + e^{2i\omega t} \int \varphi_{n’l’m’s_z’}^* e^{-2ikx} \varphi_{nlms_z} dV \right]
\end{align}
最後の変形は時間依存部分を積分の外に出すために、
\begin{align}
\cos(kx-\omega t) &\ = \frac{1}{2} \left[ e^{ikx-i\omega t} + e^{-ikx+i\omega t} \right]\\
\sin(kx-\omega t) &\ = \frac{1}{2i} \left[ e^{ikx-i\omega t} – e^{-ikx+i\omega t} \right]\\
\end{align}
と変形しているよ。ちょっと複雑になったけれども、時間依存部分はすべて積分の外に出たので、時間ステップごとに積分を実行しなくて済むね。あとは、ルンゲ・クッタ法などの常微分方程式を解く計算アルゴリズムで、この連立常微分方程式が得られるね。ちなみに、$\hat{\boldsymbol{p}}\cdot\boldsymbol{A}$ は電子の軌道運動による電磁波の吸収と放出を、$\hat{\boldsymbol{s}}\cdot\boldsymbol{B}$ は電子のスピンによる電磁波の吸収と放出を表すよ。また、$\boldsymbol{A}^2$ は電磁場の量子化後に分かるけれども、光子の２個吸収、２個放出、光子の散乱に寄与するよ。
先のポテンシャル積分項にて、スピンと２次の効果を無視すると
\begin{align}
\int \varphi_{n’l’m’}^* \hat{V}(t)\varphi_{nlm} dV = -\frac{i A_0e}{2} \left[e^{-i\omega t}\int \varphi_{n’l’m’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z \right] e^{ikx} \varphi_{nlm} dV + e^{i\omega t}\int \varphi_{n’l’m’}^* \left[
\frac{ E_{n’} – E_n }{\hbar}\, z \right] e^{-ikx} \varphi_{nlm} dV \right]
\end{align}
となるね。さらに、原子サイズに対して、波の波長が十分に大きい場合、$ e^{ikx} \simeq 1 $、$ e^{-ikx} \simeq 1$ が十分成り立つね（光子のエネルギー $10[{\rm eV}]$ の波長が約 $100 [{\rm nm}]$ なので十分だね）。積分に関係ない部分をすべて外に出すと
\begin{align}
\int \varphi_{n’l’m’}^* \hat{V}(t)\varphi_{nlm} dV = -i A_0e \frac{ E_{n’} – E_n }{\hbar} \cos(\omega t) \int \varphi_{n’l’m’}^* z \varphi_{nlm} dV
\end{align}
となって、ポテンシャル積分項は、係数を除いて、実質的に以前解説した電気双極子の行列要素と一致するね。このハミルトニアンを元に、次回は水素原子の基底状態にいる電子に電磁波を与えてみるよ。
前回解説した内容を踏まえて、外部から加える磁場を1テスラとしたときの主量子数１から３までのエネルギー準位の計算結果を示すよ。水素原子の場合、外部磁場が１テスラでスピン―軌道相互作用の効果とゼーマン効果がどちらも $10^{-5}[{\rm eV}]$ 程度となるよ。
