ここからは外場として静磁場が加わるときのシミュレーションを行いたいので、まずはハミルトニアンを復習しよう!
静電場中を運動する荷電粒子の場合、ハミルトニアンのポテンシャル項に静電ポテンシャルを加えるだけだったけれども、
静磁場中を運動する荷電粒子の場合にはこのような単純な操作だけからは導くことができないね。
一旦、電磁気学に戻って、そこからハミルトニアンを導出する必要があるよ。
電磁場中を運動する荷電粒子に加わる力(ローレンツ力)
電場を$\boldsymbol{E}$、磁場を$\boldsymbol{B}$とした電磁場中を運動する荷電粒子(電荷$q$)にはローレンツ力
\begin{align}
\boldsymbol{F} = q(\boldsymbol{E} + \dot{\boldsymbol{r}}\times \boldsymbol{B})
\end{align}
が加わるんだったね。つまり、この力によって運動する荷電粒子の運動方程式は
\begin{align}
m\ddot{\boldsymbol{r}} = q(\boldsymbol{E} + \dot{\boldsymbol{r}}\times \boldsymbol{B})
\end{align}
だね。
電磁ポテンシャルとゲージ変換
一方、電場と磁場はスカラーポテンシャル$\phi$とベクトルポテンシャル$\boldsymbol{A}$を用いて
\begin{align}
\boldsymbol{E} &= -\frac{\partial \boldsymbol{A} }{\partial t} -\nabla \phi\\
\boldsymbol{B} &= \nabla \times \boldsymbol{A}
\end{align}
と表すことができるんだったね。この2つのポテンシャルは電磁ポテンシャルと呼ばれるよ。
電磁ポテンシャルが決まると電場と磁場は一意に決まるけれども、その反対は成り立たないんだよね。
同じ電場と磁場を与えるベクトルポテンシャルは無限に存在して、任意の関数 $\chi(\boldsymbol{r},t)$ を用いて
\begin{align}
\boldsymbol{A} &= \boldsymbol{A}’ + \nabla \chi\\
\phi &= \phi’ – \frac{\partial \chi}{\partial t}
\end{align}
と変換した電磁ポテンシャルも同じ電場と磁場を与えるんだね。電磁ポテンシャルに存在する任意性はゲージ自由度って呼ばれ、上記の変換ゲージ変換って呼ばれるよ。
このゲージ自由度をうまく利用することで目的とする物理系の表式を簡単にすることもできるんだよ。例えば、
\begin{align}
\nabla \cdot \boldsymbol{A}’ + \nabla^2 \chi = 0
\end{align}
を満たすようなクーロンゲージと呼ばれる$\chi$を設定することで、ベクトルポテンシャルが必ず
\begin{align}
\nabla \cdot \boldsymbol{A} = 0
\end{align}
を満たすことを強制することができて、後に静磁場中の電子を議論する際に便利だんだよね。
電磁場中を運動するラグランジアンとハミルトニアン
この$\phi$と$\boldsymbol{A}$を用いて電磁場中の荷電粒子に対するラグランジアン$L$は次のとおりに与えられるんだったね。
\begin{align}
\boldsymbol{L} = \frac{m}{2}\, \dot{\boldsymbol{r}}^2 + \dot{\boldsymbol{r}} \cdot \boldsymbol{A} -q \phi
\end{align}
ちなみに、このラグランジアンから得られるオイラー-ラグランジュ方程式を変形することで先に上げたローレンツ力による運動方程式も導出できるよ。
ラグランジアンは位置$\boldsymbol{r}$と速度$\dot{\boldsymbol{r}}$の関数だけれども、
位置($\boldsymbol{r}$)と正準運動量($\boldsymbol{p}=(p_x,p_y,p_z)$)
\begin{align}
p_j = \frac{\partial L}{\partial \dot{x}_j} = m \dot{x}_j +q A_j
\end{align}
が変数となるようにルジャンドル変換した量がハミルトニアン
\begin{align}
H = \dot{\boldsymbol{r}} \cdot \boldsymbol{p} – L = \frac{m}{2}\, \dot{\boldsymbol{r}}^2 + q \phi = \frac{1}{2m} (\boldsymbol{p} – q \boldsymbol{A})^2 + q \phi
\end{align}
だよ。ここまでは古典力学の範囲だけれども、この位置と正準運動量を演算子に置き換えて、交換関係$[\hat{x}_i, \hat{p}_j] = i\hbar \delta_{ij}$を課したのが量子力学版ハミルトニアン
\begin{align}
\hat{H} = \frac{1}{2m} (\hat{\boldsymbol{p}} – q \boldsymbol{A})^2 + q \phi
\end{align}
だね。そしてこのハミルトニアンに対するシュレーディンガー方程式は次のとおりだよ。
\begin{align}
i\hbar \frac{\partial }{\partial t}\psi(\boldsymbol{r}, t) = \hat{H} \psi(\boldsymbol{r}, t)
\end{align}
ちなみにこのような古典力学系から量子化する手順は正準量子化と呼ばれ、任意の古典力学系を量子化することができるよ。
静磁場中の電子のハミルトニアン
静磁場中の電子($q=-e$)の運動を調べるには、真空中の電子の場合にはスカラーポテンシャルをゼロ( $\phi = 0$ )、原子核に束縛されている場合にはクーロンポテンシャルを与えれば良いね。
今回、水素原子に束縛された電子を対象とするので、
\begin{align}
\hat{H} = \frac{1}{2m} (\hat{\boldsymbol{p}} + e \boldsymbol{A})^2 + V( r )
\end{align}
これがハミルトニアンだよ。さらに、先に挙げたクーロンゲージを適用すると$\hat{\boldsymbol{p}} \cdot \boldsymbol{A} =\boldsymbol{A} \cdot \hat{\boldsymbol{p}}$を満たすため、
\begin{align}
\hat{H} = \frac{1}{2m} ( \hat{\boldsymbol{p}}^2 +2e\boldsymbol{A}\cdot\hat{\boldsymbol{p}} + e^2 \boldsymbol{A}^2) + V( r )
\end{align}
となるよ。
一方、磁場の向きをz軸方向とすると$\boldsymbol{B} = (B_x, B_y, B_z)$は
\begin{align}
B_x &= \frac{\partial A_z}{\partial y} – \frac{\partial A_z}{\partial y} = 0\\
B_y &= \frac{\partial A_x}{\partial z} – \frac{\partial A_z}{\partial x} = 0\\
B_z &= \frac{\partial A_y}{\partial x} – \frac{\partial A_x}{\partial y} = {\rm Const.}
\end{align}
だけれども、これを生み出すベクトルポテンシャル $\boldsymbol{A} = (A_x, A_y, A_z )$ はクーロンゲージを課してもなお無数に存在して、例えば次の3つ
\begin{align}
\boldsymbol{A} &= (-B_zy\,,0\,,0)\\
\boldsymbol{A} &= (0,\,B_zx\,,0)\\
\boldsymbol{A} &= \left(-\frac{1}{2} B_zy\,, \frac{1}{2} B_zx \,, 0 \right)
\end{align}
は、クーロンゲージを満たしつつ、どれも同じ$\boldsymbol{B} = (0, 0, B_z)$を与えるんだよね。
前2つはランダウゲージ、最後のは対象ゲージと呼ばれているよ。
この対象ゲージを採用すると、先のハミルトニアンの$\boldsymbol{A}\cdot\hat{\boldsymbol{p}}$は、角運動量演算子$\hat{\boldsymbol{L}} = (\hat{L_x}, \hat{L_y}, \hat{L_z})$を用いて
\begin{align}
\boldsymbol{A}\cdot\hat{\boldsymbol{p}} = A_x \hat{p}_x + A_y \hat{p}_y + A_z \hat{p}_z = \frac{1}{2} B_z \left( x \hat{p}_y -y\hat{p}_x \right) = \frac{1}{2} B_z \hat{L}_z
\end{align}
と変形することができるよ。もともと磁場の向きはどちらでも良いので、$\frac{1}{2} B_z \hat{L}_z $ を $\boldsymbol{B}\cdot \hat{\boldsymbol{L}}$ と置き直せば、
\begin{align}
\hat{H} = \frac{1}{2m} ( \hat{\boldsymbol{p}}^2 + e\boldsymbol{B}\cdot \hat{\boldsymbol{L}} + e^2 \boldsymbol{A}^2) + V( r )
\end{align}
となるよ。このハミルトニアンは磁場が時間に依存しない静磁場を想定したけれども、磁場が時間に依存しても各時間ステップごとに対象ゲージの関係を満たしていると考えれば、特に問題なく成り立つと考えられるね。さらに、静電場が存在しても静電場によるポテンシャルエネルギーを$V( r )$加えても成り立つし、時間変化する電場が存在してもその影響はベクトルポテンシャル$\boldsymbol{A}$に含まれるね。つまり、このハミルトニアンは任意の電磁場中に存在する電子でそのまま成り立つよ。
$\boldsymbol{B}\cdot \hat{\boldsymbol{L}}$ の意味
$\boldsymbol{B}$ は外部磁場、$\hat{\boldsymbol{L}}$ は電子の角運動量を表す演算子なので、
古典力学と対比させると $\boldsymbol{B}\cdot \hat{\boldsymbol{L}}$ は電子の角運動量で生じる磁気モーメント$\boldsymbol{M}$と磁場との相互作用で生じるエネルギー変化分
\begin{align}
\Delta E = – \boldsymbol{B} \cdot \boldsymbol{M}
\end{align}
と考えることができるので、電子の角運動量演算子$\hat{\boldsymbol{L}}$に対する磁気モーメントの演算子$\hat{\boldsymbol{M}}$は
\begin{align}
\hat{\boldsymbol{M}} = -\frac{e}{2m} \hat{\boldsymbol{L}}
\end{align}
と関係があると言えるね。ちなみに $\hat{\boldsymbol{M}}$ は軌道磁気モーメント、$\boldsymbol{B} \cdot \boldsymbol{M}$はゼーマン項って呼ばれるよ。
静磁場中の電子のハミルトニアンの固有状態
任意の電磁場中の水素原子殻に束縛された電子のハミルトニアンは、電磁場が存在しない場合の固有状態が既知のハミルトニアン$\hat{H}_0$を用いて
\begin{align}
\hat{H} = \hat{H}_0 + \frac{e}{2m} \boldsymbol{B}\cdot \hat{\boldsymbol{L}} + \frac{e}{2m} \boldsymbol{A}^2
\end{align}
と表されるね。静磁場を$\boldsymbol{B} = (0,0,B_z)$と表すと、
\begin{align}
\hat{H} = \hat{H}_0 + \frac{eB}{2m} \hat{L}_z + \frac{e^2B_z^2}{8m} (\hat{x}^2 + \hat{y}^2)
\end{align}
となるね(第3項目は対称ゲージを採用しているよ)。第2項目の$\hat{L}_z$は電磁場が存在しない場合の固有関数で
\begin{align}
\hat{L}_z \varphi_{nlm} = \hbar m \varphi_{nlm}
\end{align}
という固有状態となっているから、第3項目を無視するとハミルトニアンはすでに次のようにエネルギー固有状態として解けていることになるよ。
\begin{align}
\hat{H} \varphi_{nlm} = (E_{n} + m \hbar \omega_L )\varphi_{nlm}
\end{align}
ちなみに$\omega_L$は次の式で定義される量でラーモア角振動数って呼ばれるよ。
\begin{align}
\omega_L \equiv \frac{eB}{2m}
\end{align}
つまり、縮退していたエネルギー準位は静磁場を加えることで磁気量子数 $m$ に比例した量だけ変化して縮退が解けることがわかったね。
このような静磁場によるエネルギーシフトは正常ゼーマン効果と呼ばれるよ。
ちなみに上記の議論は、外部磁場が $B^2\ll B$ の場合に正当化されるよ。
一方、外部磁場が大きくなると、ハミルトニアンの第3項目が無視できずに
\begin{align}
\left[ \hat{H}_0 + \frac{eB}{2m} \hat{L}_z + \frac{e^2}{8m} (\hat{x}^2 + \hat{y}^2) \right] \psi = E \psi
\end{align}
という固有方程式を解く必要があるね。
外場として磁場が加えられたときの固有方程式の解き方
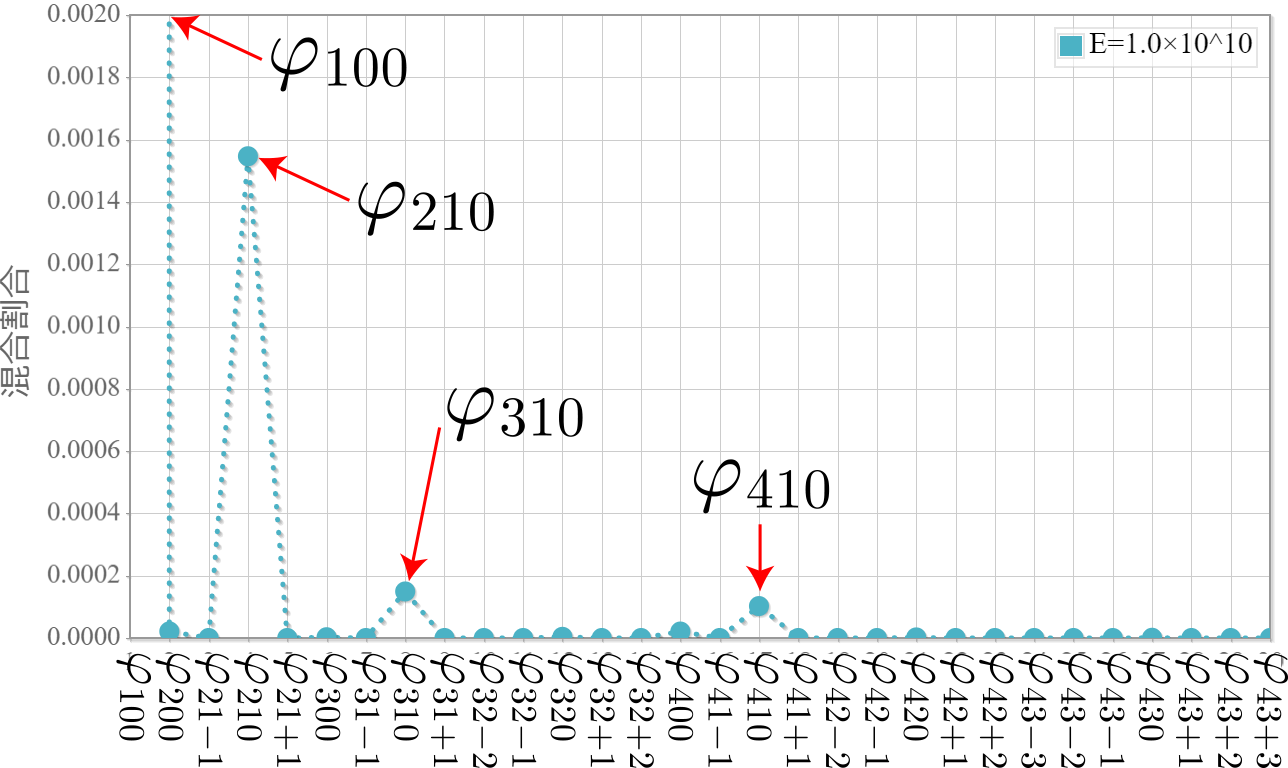
ここからは外場として静電場が加えられたときと同じ手順で進めるよ。外場として磁場が加えられたときの固有関数は外場がない場合の正規直交完全系をなす固有関数$\varphi_{nlm}$の重ね合わせ
\begin{align}
\psi = \sum_{n, l, m} a_{nlm} \varphi_{nlm}
\end{align}
と表わすことができるよ。$a_{nlm}$は展開係数だね。
展開係数が決定できれば固有方程式を解いたことになるので、展開係数に関する方程式を導く必要があるよ。
まずは代入して、
\begin{align}
\sum_{n, l, m} a_{nlm} \left[ E_{n} + m \hbar \omega_L + V \right] \varphi_{nlm} = E \sum_{n, l, m} a_{nlm} \varphi_{nlm}
\end{align}
そして、両辺に$\varphi_{nlm}$の複素共役$\varphi_{n’l’m’}^*$を掛けて全空間で積分すると
\begin{align}
(E_{n’} + m’ \hbar \omega_L)a_{n’l’m’} + \sum_{n, l, m}a_{nlm} V^{n’l’m’}_{nlm} = E a_{n’l’m’}
\end{align}
となって、$a_{n’l’m’}$に関する連立方程式が導かれるんだね。$V^{n’l’m’}_{nlm}$は式を簡略化するために改めて定義した
\begin{align}
V^{n’l’m’}_{nlm} \equiv \int_0^\infty\!\!\! r^2 dr \int_0^\pi \!\!\! \sin\theta d\theta \int_0^{2\pi} \!\!\! d\phi \left[\varphi_{n’l’m’}^* V \varphi_{nlm} \right]
\end{align}
だよ。連立方程式は行列で表すとわかりやすくなるので、エネルギーの小さい順に固有関数の係数を並べると次のようになるよ。
\begin{align}
\left(\matrix{ E_1 +V_{100}^{100} & V_{200}^{100}& V_{21-1}^{100} & V_{210}^{100} & V_{211}^{100} & \cdots \cr
V_{100}^{200} & E_2 + V_{200}^{200}& V_{21-1}^{200} & V_{210}^{200} &V_{211}^{200} &\cdots \cr
V_{100}^{21-1} & V_{200}^{21-1} & E_2 -\hbar \omega_L + V_{21-1}^{21-1} & V_{210}^{21-1}& V_{211}^{21-1}& \cdots \cr
V_{100}^{210} & V_{200}^{210} & V_{21-1}^{210} & E_2 + V_{210}^{210}& V_{211}^{210}& \cdots \cr
V_{100}^{211} & V_{200}^{211} & V_{21-1}^{211} & V_{210}^{211}& E_2 + \hbar \omega_L+ V_{211}^{211}& \cdots \cr
\vdots & \vdots & \vdots & \vdots & \vdots & \ddots } \right) \left(\matrix{ a_{100} \cr a_{200} \cr a_{21-1} \cr a_{210} \cr a_{211} \cr \vdots }\right) = E \left(\matrix{ a_{100} \cr a_{200} \cr a_{21-1} \cr a_{210} \cr a_{211} \cr \vdots }\right)
\end{align}
まさに行列表した固有値方程式の形になっているのがわかるね。
これで固有値と固有ベクトルを計算すると、固有値はそのまま外場が加えられた場合のエネルギー、固有ベクトルがそのまま展開係数の値そのものになるね。
次回は、外場として磁場を加えたときの様子をシミュレーションします!
まとめと今後の予定
わかったこと
- 静磁場が弱い場合には固有状態は静磁場が存在しない場合と同じ。
- 静磁場が強い場合でも数値計算で固有状態を計算することができる。
今後の予定(宿題メモ)
- 今度は外場として時間に依存しない磁場を加えてみよう!
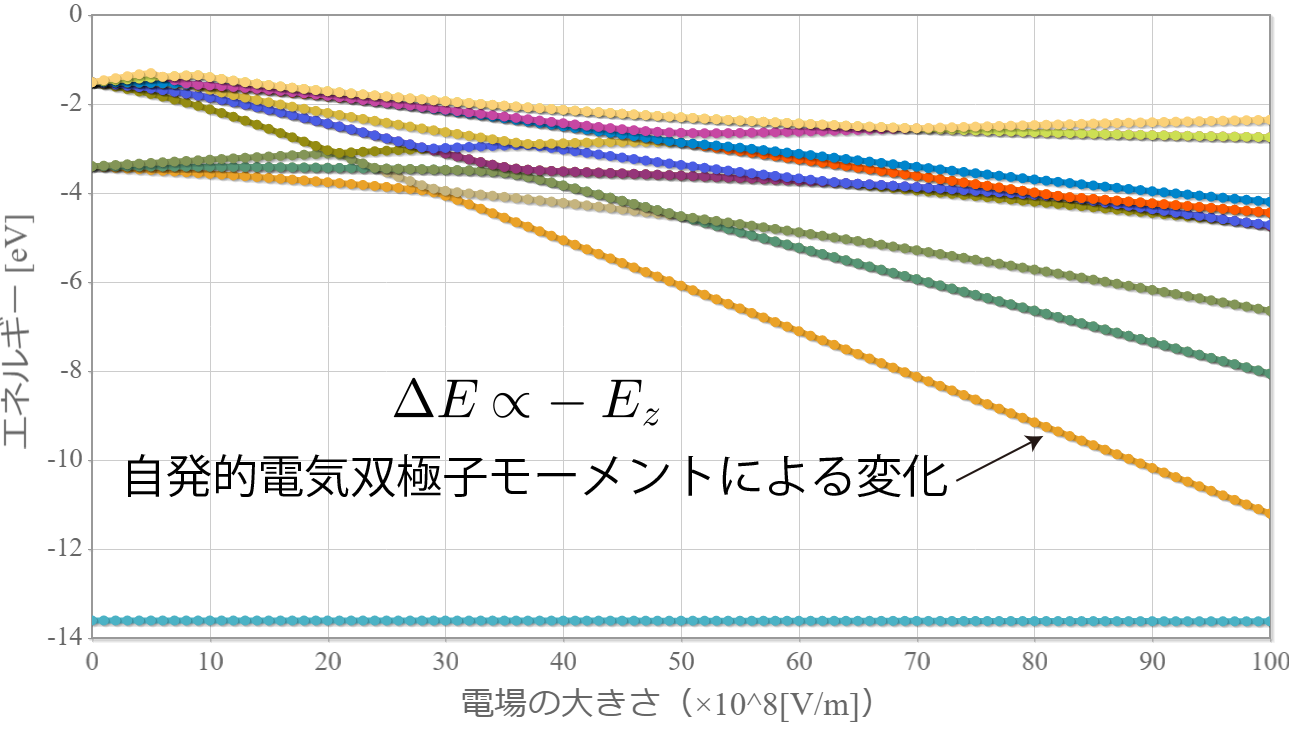
- 1次のシュタルク効果を示す電気双極子の分極率を調べてみよう!
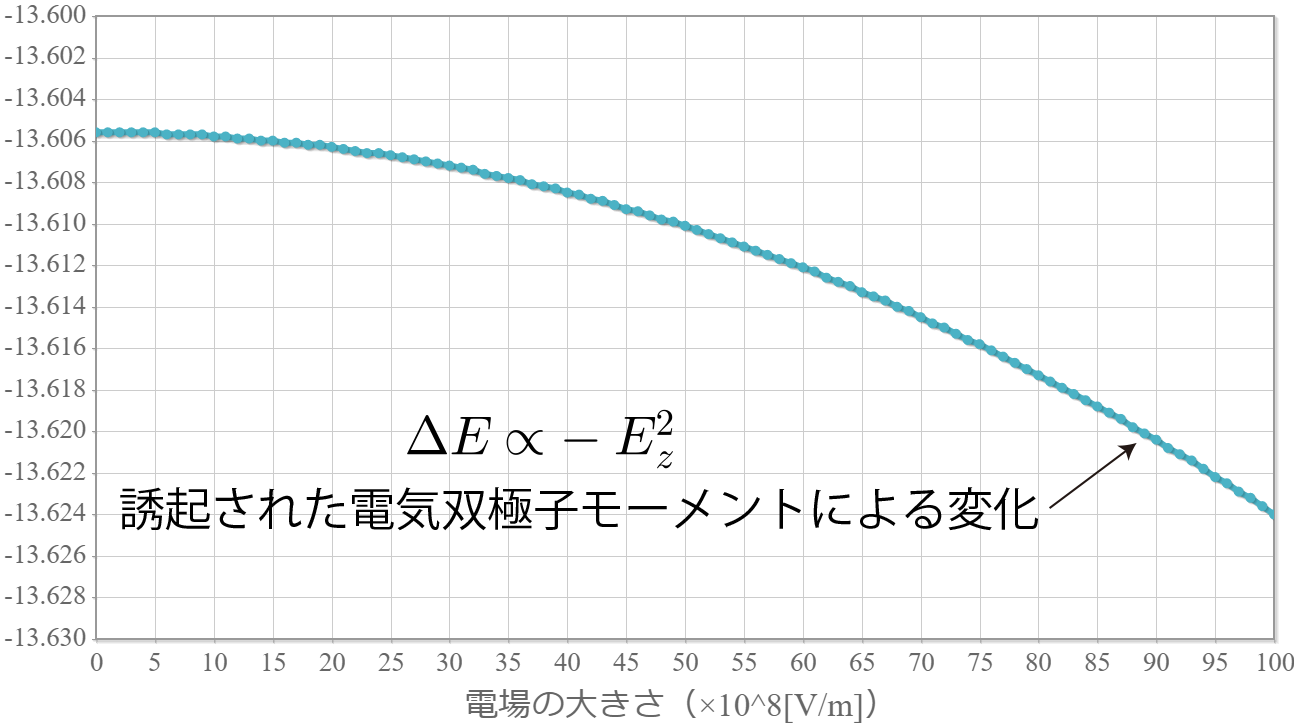
- 2次のシュタルク効果で生じる電気双極子の分極率を調べてみよう!
- 電場をもっともっと強くしたときの状態(電離状態との結合)を調べてみよう!