タグ: ヘリウム原子

前回を踏まえて、ヘリウム原子基底状態の動径確率密度分布を計算したので、報告するよ。次のグラフでは、ヘリウム原子基底状態に対する動径確率密度分布は２種類用意したよ。１つ目は「２つの電子のどちらかがその距離にいる確率密度（ 青色：$\bar{P}_{100}^{Z=2}(r) $ ）」、２つ目は「１つの電子が原点にいて、もう一つの電子がその距離にいる確率密度（ 橙色：$P_{100}^{Z=2}(0,r) $ ）」。あと比較対象として、「水素原子基底状態に対する動径確率密度分布（$P_{100}^{Z=1}(r) $）」と「ヘリウム原子イオンの基底状態に対する動径確率密度分布（$P_{100}^{Z=2}(r) $）」を同時にプロットしたよ。

横軸が原点からの距離、縦軸が確率密度だよ。一番強く原子核に束縛されているのが「ヘリウム原子イオンの基底状態」で、反対に最も束縛されていないのが「水素原子の基底状態」だね。つまり、原子核の電荷が $Z=2$ で電子が１個の場合が一番強く束縛されて、$Z=1$ で電子が１個の場合が最も束縛が弱いね。２種類用意したヘリウム原子を比較すると、１個を原点に存在する「橙色：$P_{100}^{Z=2}(0,r) $」は、他方の「青色：$\bar{P}_{100}^{Z=2}(r) $」と比較して、電子間の反発でより遠くに存在することがわかるね。

「ヘリウム原子のエネルギー固有状態の計算方法」に基づいて、ヘリウム原子のエネルギー準位と固有関数の空間分布を計算したよ。「ヘリウム原子の基底状態の計算結果」で示したとおり、計算結果はよく知られた精密な実験結果とかなり一致しているよ。

ヘリウム原子のエネルギー準位

次の図は、パラ（対称関数・スピン１重項）とオルト（反対称関数・スピン３重項）の主量子数 $n=1,2,3$
のエネルギー準位だよ。オルトのほうがパラよりも若干小さな値となるね。これは交換相互作用の結果だね。イオン化エネルギーは、電子２個の基底状態から電子１個を引き離すために必要なエネルギーで、「基底状態エネルギー（$-79.18[{\rm
eV}]$）」から「電子が１個のみのヘリウム原子の基底状態エネルギー（ $-54.4[{\rm eV}]$ ）」で計算できるよ。

ヘリウム原子の固有状態の空間分布

今回も独立電子近似の場合と同様、粒子の１つが
$\varphi_{100}(\boldsymbol{r})|$の最も確率の高い原点（ $\boldsymbol{r}_1=0$ あるいは $\boldsymbol{r}_2=0$
）に存在するとして、他方の粒子の空間確率密度を描画するよ。最初の表がパラヘリウム（対称関数・スピン1重項）、次の表がオルトヘリウム（反対称関数・スピン3重項）だよ。

（※実際の表はこちらのページを見てね！）

ちなみにヘリウム原子の場合、直交関数系は $(1,0,0)$ を必ず含むよ。なぜならば、$(1,0,0)$ から次に低い $(2,0,0)$ とした場合の固有エネルギーは約 $-20[{\rm eV}]$
で、イオン化エネルギーよりも高くなるために実質的には先に電離してしまうね。

独立電子近似の場合、ヘリウム原子の２つの電子の波動関数は、個々の水素様原子（ $Z=2$ ）の波動関数の積を用いて、空間対称（スピン３重項／パラ）あるいは空間反対称（スピン１重項／オルト）の２つの状態をとるよ。具体的な波動関数の表式はそれぞれ

\begin{align}
\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) + \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1l_1m_1}(\boldsymbol{r}_1)\varphi_{n_2l_2m_2}(\boldsymbol{r}_2) – \varphi_{n_1l_1m_1}(\boldsymbol{r}_2)\varphi_{n_2l_2m_2}(\boldsymbol{r}_1)\right] \\
\end{align}

と表されるね。この波動関数は各粒子ごとに３次元で合計で６次元の関数なので、これを描画するには工夫が必要になるよ。１番基本的な考え方は、空間位置 $ \boldsymbol{r} $ に粒子１あるいは粒子２が存在する空間確率密度を

\begin{align}
\rho( \boldsymbol{r} ) = \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}_1, \boldsymbol{r}) |^2 dV_1 + \frac{1}{2} \int |\chi_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, \boldsymbol{r}_2) |^2 dV_2
\end{align}

と定義することで、空間分布を計算することができるね。ただし、これを先の $\chi^{(S)}$ と $\chi^{(A)}$ に適用すると、

\begin{align}
\rho^{(S)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2\\
\rho^{(A)}( \boldsymbol{r} ) &\ = |\varphi_{n_1l_1m_1}(\boldsymbol{r})|^2 + |\varphi_{n_2l_2m_2}(\boldsymbol{r})|^2
\end{align}

となって、それぞれの粒子の空間分布の和となるね。ヘリウム原子の低エネルギーの状態は、粒子の片方は必ず $(n,l,m)=(1,0,0)$ に存在するので、先の空間確率密度を数値的に計算すると、他方の粒子がどの準位に存在したとしても、 $|\varphi_{100}(\boldsymbol{r})|^2 >> |\varphi_{nlm}(\boldsymbol{r})|^2 $ となって、実質的に $|\varphi_{100}(\boldsymbol{r})|^2$ となってしまうね。これは、２つの粒子が存在する確率が $|\varphi_{100}(\boldsymbol{r})|^2$ で表される領域に集中していることを意味しているよ。

そこで今回は、粒子の１つが $\varphi_{100}(\boldsymbol{r})|$の最も確率の高い原点（ $\boldsymbol{r}_1=0$ あるいは $\boldsymbol{r}_2=0$ ）に存在するとして、他方の粒子の空間確率密度

\begin{align}
\rho^{(S)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(S)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r}, 0)|^2 \\
\rho^{(A)}( \boldsymbol{r} ) = \frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(0, \boldsymbol{r})|^2 +\frac{1}{2}|\chi^{(A)}_{(n_1l_1m_1)(n_2l_2m_2)}(\boldsymbol{r},0)|^2
\end{align}

を定義して、空間分布を描画したよ。ちなみに両者とも第１項目と第２項目の値は同じ値となるよ。

（※実際の表はこちらのページを見てね！）

上記の結果は単に $|\varphi_{nlm}(\boldsymbol{r})|^2$ を計算した結果に似ているけれども異なるよ。空間対称関数と空間反対称関数では、概ね同じだけれども顕著に異なるのが、２個目の粒子の状態が $(n,l,m) =(2,0,0)$ や $(n,l,m) =(3,0,0)$ で、原点を中心に存在する場合だね。これは、空間対称関数の場合には、同じ領域に居ようとするけれども、空間反対称関数の場合には、互いに避けようとする結果だね。次回は、電子間の相互作用を加味した波動関数を描画するよ。

前回、ヘリウム原子の電子状態の計算方法を示したね。その計算結果のうち、今回は基底状態を示すよ。ヘリウムの基底状態は２つの電子のスピンが上向きと下向きの反対称で、波動関数の空間部分は対称関数となるね。そのため、正規直交完全系をなす対称関数で展開して

\begin{align}
\psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \sum_{\alpha,\alpha’} s_{\alpha\alpha’}\chi^{(S)}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

エネルギー固有状態を計算したよ。その結果、基底状態のエネルギー固有値が $ E_{\rm calculate} = -79.18 [{\rm eV}]$ となって、よく知られた実験値 $E_{\rm experiment } = -78.98 [{\rm eV}] $ と比較してわずか $0.2\%$ のずれの結果を得ることができたよ。

計算結果：ヘリウム原子の基底状態

基底状態の固有関数は、水素様原子 $(1s)^2$ の固有関数 $\chi^{(S)}_{1s1s}$ と $(1s)(2s)$ の固有関数 $\chi^{(S)}_{1s2s}$の２つの項の重ね合わせ

\begin{align}
\psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) = s_{1s1s}\chi^{(S)}_{1s1s}(\boldsymbol{r}_1, \boldsymbol{r}_2) + s_{1s2s}\chi^{(S)}_{1s2s}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

で、$ s_{1s1s} \simeq 0.922 \ , \ s_{1s2s} \simeq -0.384 $ の場合に

\begin{align}
E_{\rm calculate} =\int \!\!\! \int \psi^{(S)}(\boldsymbol{r}_1,\boldsymbol{r}_2)^* \hat{H} \psi^{(S)}(\boldsymbol{r}_1,\boldsymbol{r}_2) dV_1dV_2 \simeq -79.18 [{\rm eV}]
\end{align}

となるよ。この結果は、非摂動１電子近似の $ -108.8 [{\rm eV}] $、１次の摂動近似の $-74.8 [{\rm eV}]$、１電子近似に変分法を適用した $-77.5[{\rm eV}]$ と比較して、実験結果を非常によく一致しているね。つまり、ヘリウム原子の基底状態は $ |s_{1s1s}|^2 \simeq 0.850 \ , \ |s_{1s2s}|^2 \simeq 0.147 $ の割合で水素様原子固有状態 $\chi^{(S)}_{1s1s}$ と $\chi^{(S)}_{1s2s}$ の状態が重ね合わさった状態であることがわかったよ。ちなみに $\chi^{(S)}_{1s1s}$ と $\chi^{(S)}_{1s2s}$ は次のとおりだよ。

\begin{align}
\chi^{(S)}_{1s1s}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \varphi_{100}(\boldsymbol{r}_1)\varphi_{100}(\boldsymbol{r}_2)\\
\chi^{(S)}_{1s2s}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}}\left[\varphi_{100}(\boldsymbol{r}_1)\varphi_{200}(\boldsymbol{r}_2)+\varphi_{100}(\boldsymbol{r}_2)\varphi_{200}(\boldsymbol{r}_1)\right]
\end{align}

ヘリウム原子の電子の波動関数は２変数関数なので、３次元空間で波動関数を表すことが単純にはできないね。次回、波動関数の可視化を工夫してみよう。また、ヘリウム原子の電子のエネルギー準位を整理してまとめるよ。

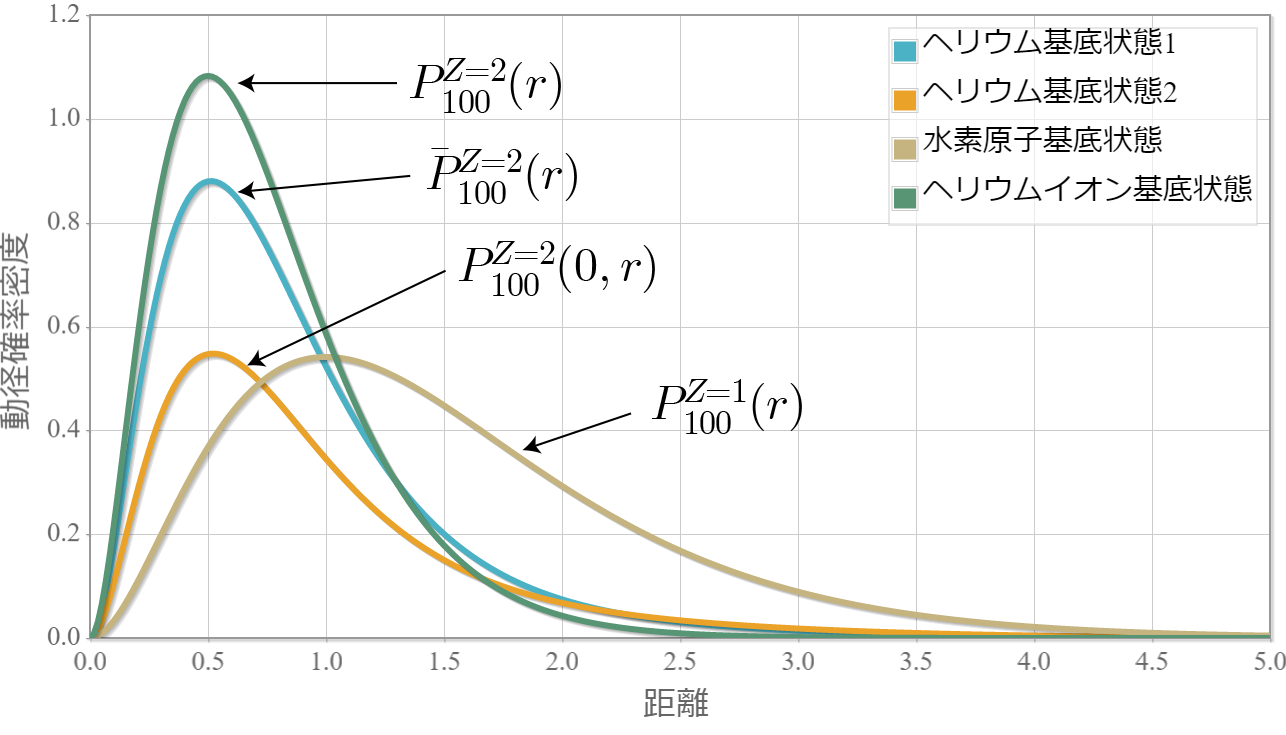
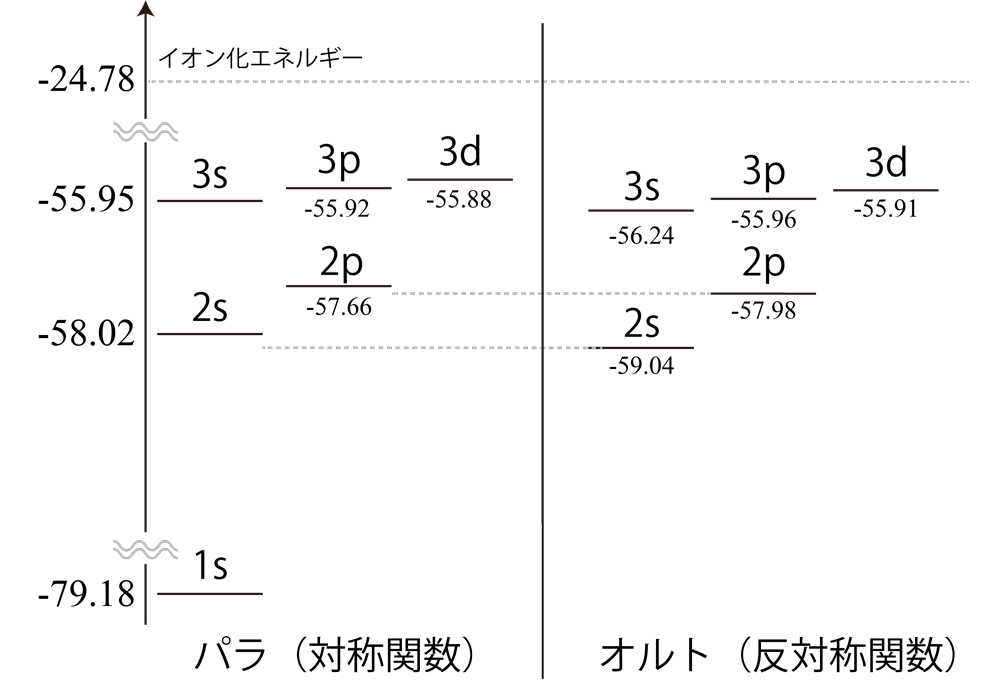
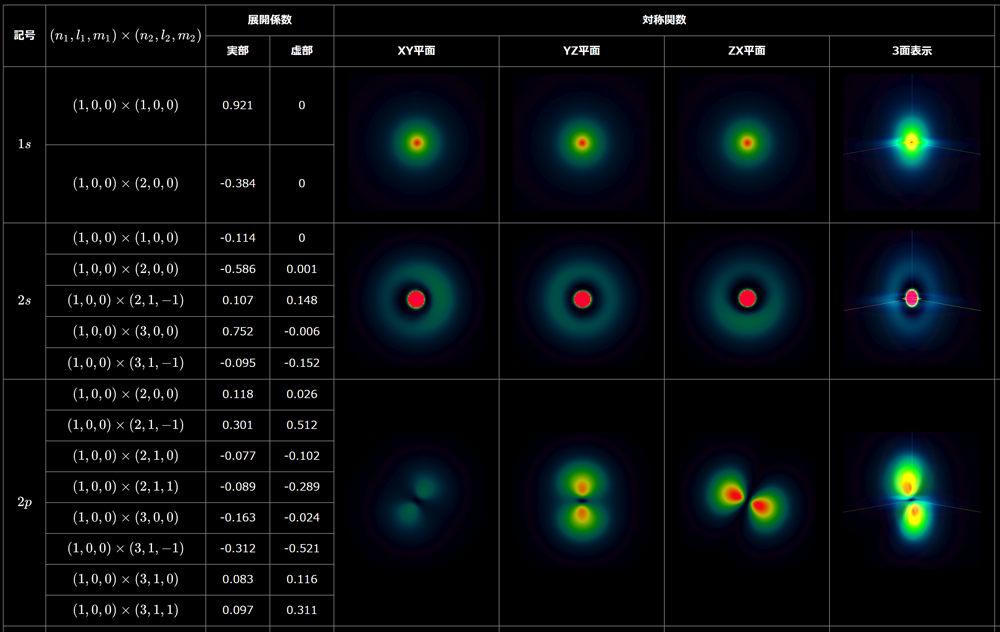
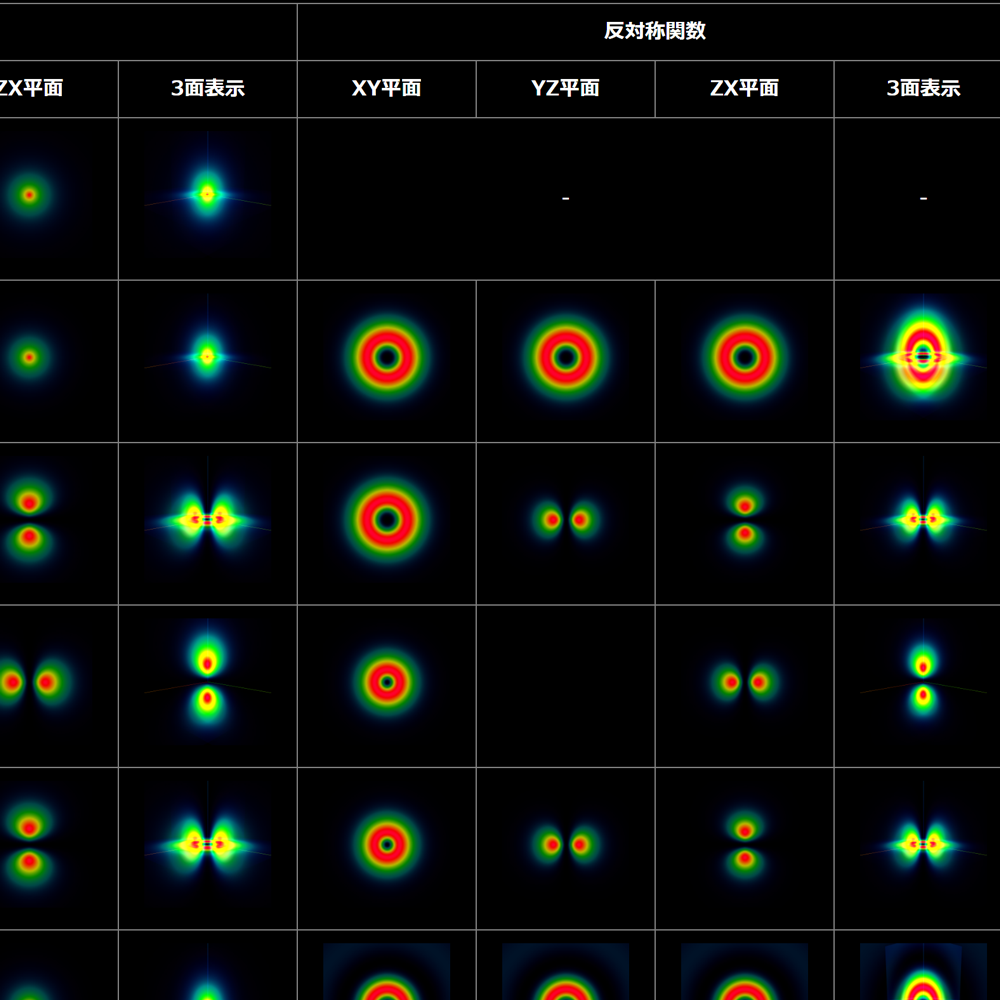
水素原子に束縛した電子の固有状態は解析的に計算することができるけれども、ヘリウム原子に束縛された２個の電子の固有状態は解析的には無理であることが知られているよ。ハミルトニアンは次のとおりだよ。

\begin{align}
H &\ = \frac{\hat{\boldsymbol{p}_1}^2}{2m_e} -\frac{q^2Z}{4\pi \epsilon_0|\boldsymbol{r}_1|} + \frac{\hat{\boldsymbol{p}_2}^2}{2m_e} -\frac{q^2Z}{4\pi \epsilon_0|\boldsymbol{r}_2|} + \frac{q^2}{4\pi \epsilon_0|\boldsymbol{r}_1-\boldsymbol{r}_2|}\\
&\ = H_1(\boldsymbol{r}_1) + H_2(\boldsymbol{r}_2) + H_{12}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

ハミルトニアンのうち、１番目の電子のみと２個目の電子のみに依存する部分をそれぞれ $H_1$、$H_2$ として、両電子に依存する部分を $H’$ とに分けているよ。この第３項目が存在することで、見た目よりも複雑だよ。このハミルトニアンの固有状態の数値計算方法でよく用いられるは、ハートリー＝フォック方程式と呼ばれる多電子系のシュレーディンガー方程式を平均場を導入することで１体問題と近似して計算する方法だね。今回は、平均場を導入することなしに２個の電子の固有状態を計算する方法を考えるよ。

空間対称関数と空間反対称関数を用いたエネルギー固有方程式

電子のようなフェルミ粒子は、スピン座標も含めた電子座標を入れ替えた固有状態は、反対称である必要があるね。そのため、空間部分はスピン座標が対称か非対称かによって、空間座標も対称か非対称しか取りえないね。

\begin{align}
\chi^{S}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_1(\boldsymbol{r}_1)\varphi_2(\boldsymbol{r}_2) + \varphi_1(\boldsymbol{r}_2)\varphi_2(\boldsymbol{r}_1) \right)\\
\chi^{A}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_1(\boldsymbol{r}_1)\varphi_2(\boldsymbol{r}_2) – \varphi_1(\boldsymbol{r}_2)\varphi_2(\boldsymbol{r}_1) \right)
\end{align}

展開する関数を、水素原子に束縛された電子の固有状態 $\varphi_{nlm}$ を用いると、

\begin{align}
\chi^{S}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_{nlm}(\boldsymbol{r}_1)\varphi_{n’l’m’}(\boldsymbol{r}_2) +
\varphi_{nlm}(\boldsymbol{r}_2)\varphi_{n’l’m’}(\boldsymbol{r}_1) \right)\\
\chi^{A}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_{nlm}(\boldsymbol{r}_1)\varphi_{n’l’m’}(\boldsymbol{r}_2) –
\varphi_{nlm}(\boldsymbol{r}_2)\varphi_{n’l’m’}(\boldsymbol{r}_1) \right)
\end{align}

と表すことができるね。今後の表記を簡単にするために量子数 $nlm$ をまとめて $\alpha $ と表すことにするね。

\begin{align}
\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) +
\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)\\
\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( \varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) –
\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)
\end{align}

$\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)$ と $\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)$ は、それぞれ異なる量子数のもとの次のような直交関係があるね。

\begin{align}
&\ \int\!\!\!\int \chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* \chi^{S}_{\alpha_3\alpha_4}(\boldsymbol{r}_1, \boldsymbol{r}_2) dV_1dV_2 \\
&\ =
\frac{1}{2}\int\!\!\!\int \left[ \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_2}^*(\boldsymbol{r}_2) + \varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_2}^*(\boldsymbol{r}_1) \right] \left[ \varphi_{\alpha_3}(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_2) + \varphi_{\alpha_3}(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_1) \right]dV_1dV_2 \\
&\ = \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int \varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2
+ \frac{1}{2}\int \varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2\\
&\ + \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2
+ \frac{1}{2}\int\varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2\\
&\ = \delta_{\alpha_1\alpha_3} \delta_{\alpha_2\alpha_4} + \delta_{\alpha_2\alpha_3} \delta_{\alpha_1\alpha_4}
\end{align}
\begin{align}
&\ \int\!\!\!\int \chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* \chi^{A}_{\alpha_3\alpha_4}(\boldsymbol{r}_1, \boldsymbol{r}_2) dV_1dV_2\\
&\ =
\frac{1}{2}\int\!\!\!\int \left[ \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_2}^*(\boldsymbol{r}_2) –
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_2}^*(\boldsymbol{r}_1) \right] \left[
\varphi_{\alpha_3}(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_2) –
\varphi_{\alpha_3}(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_1) \right]dV_1dV_2 \\
&\ = \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2
– \frac{1}{2}\int \varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2\\
&\ – \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2
+ \frac{1}{2}\int\varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2\\
&\ = \delta_{\alpha_1\alpha_3} \delta_{\alpha_2\alpha_4} – \delta_{\alpha_2\alpha_3} \delta_{\alpha_1\alpha_4}
\end{align}

\begin{align}
&\ \int\!\!\!\int \chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* \chi^{A}_{\alpha_3\alpha_4}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 \\
&\ =
\frac{1}{2}\int\!\!\!\int \left[ \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_2}^*(\boldsymbol{r}_2) +
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_2}^*(\boldsymbol{r}_1) \right] \left[
\varphi_{\alpha_3}(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_2) –
\varphi_{\alpha_3}(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_1) \right]dV_1dV_2 \\
&\ = \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2
+ \frac{1}{2}\int \varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2\\
&\ – \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2
– \frac{1}{2}\int\varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2\\
&\ = 0
\end{align}
\begin{align}
&\ \int\!\!\!\int \chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* \chi^{S}_{\alpha_3\alpha_4}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 \\
&\ =
\frac{1}{2}\int\!\!\!\int \left[ \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_2}^*(\boldsymbol{r}_2) –
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_2}^*(\boldsymbol{r}_1) \right] \left[
\varphi_{\alpha_3}(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_2) +
\varphi_{\alpha_3}(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_1) \right]dV_1dV_2 \\
&\ = \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2
– \frac{1}{2}\int \varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_2)\varphi_{\alpha_4}(\boldsymbol{r}_2) dV_2\\
&\ + \frac{1}{2}\int \varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_2}^*(\boldsymbol{r}_2)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2
– \frac{1}{2}\int\varphi_{\alpha_2}^*(\boldsymbol{r}_1)\varphi_{\alpha_4}(\boldsymbol{r}_1) dV_1\int
\varphi_{\alpha_1}^*(\boldsymbol{r}_1)\varphi_{\alpha_3}(\boldsymbol{r}_2) dV_2\\
&\ = 0
\end{align}

対称関数の場合、$ \alpha_1 = \alpha_2 = \alpha_3 = \alpha_4 $ を満たす時に上記の直交積分は「２」になってしまうので、条件に応じて定義を変えておく必要があるね。

\begin{align}
\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \left\{ \matrix{ \varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha}(\boldsymbol{r}_2) & \alpha = \alpha’ \cr \frac{1}{\sqrt{2}} \left( \varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) +\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right) & \alpha \ne \alpha’}\right.
\end{align}

$\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)$ と $\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)$ を構成する関数は、元々正規直交完全系を成す関数系なので、この対称関数と反対称関数を新たな基底関数とする正規直交系を考えることができるね。つまり、ヘリウム原子の電子に対する波動関数を

\begin{align}
\psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \sum_{\alpha,\alpha’}
s_{\alpha\alpha’}\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) \\
\psi^{(A)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \sum_{\alpha,\alpha’}
a_{\alpha\alpha’}\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) \\
\end{align}

として、ハミルトニアンによる固有方程式

\begin{align}
H\psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = E \psi^{(S)}(\boldsymbol{r}_1, \boldsymbol{r}_2) \\
H\psi^{(A)}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = E \psi^{(A)}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

からエネルギー固有状態を考えることができそうだね。

ハミルトニアンと対称関数・反対称関数との関係

エネルギー固有状態を計算するために必要な、各項の関係をまずは押さえておこう。対称関数は、ハミルトニアン $H_1$ と $H_2$ とは

\begin{align}
H_1 \chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( E_{\alpha}\varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) +E_{\alpha’}\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)\\
H_2 \chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( E_{\alpha’}\varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) +E_{\alpha}\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)
\end{align}

のように固有状態にはなっていないけれども、足し算すると

\begin{align}
(H_1 + H_2)\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) = ( E_{\alpha}+ E_{\alpha’})\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

というふうに、エネルギー固有状態になっているね。同様に、反対称関数の場合も

\begin{align}
H_1 \chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( E_{\alpha}\varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) – E_{\alpha’}\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)\\
H_2 \chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = \frac{1}{\sqrt{2}} \left( E_{\alpha’}\varphi_{\alpha}(\boldsymbol{r}_1)\varphi_{\alpha’}(\boldsymbol{r}_2) – E_{\alpha}\varphi_{\alpha}(\boldsymbol{r}_2)\varphi_{\alpha’}(\boldsymbol{r}_1) \right)
\end{align}

となるので、足し算すると

\begin{align}
(H_1 + H_2)\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) = ( E_{\alpha} + E_{\alpha’})\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

というふうに、エネルギー固有状態になっているね。つまり、ハミルトニアンの前半２つの項は、これら対称関数と反対称関数で固有状態となっているので、これまで水素原子に外場を加えたときの固有状態を計算したときの手順がそのまま適用できそうだね。 エネルギー固有方程式

\begin{align}
\sum_{\alpha,\alpha’} (H_1 + H_2 + H_{12}) s_{\alpha\alpha’}\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1,
\boldsymbol{r}_2) &\ = E
\sum_{\alpha,\alpha’} s_{\alpha\alpha’}\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) \\
\sum_{\alpha,\alpha’} (H_1 + H_2 + H_{12})a_{\alpha\alpha’}\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2) &\ = E
\sum_{\alpha,\alpha’} a_{\alpha\alpha’}\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)
\end{align}

の両辺に $\chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* $ と $\chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* $をそれぞれ掛けて、全空間で積分すると、

\begin{align}
s_{\alpha_1\alpha_2} (E_1 + E_2) +
\sum_{\alpha,\alpha’} s_{\alpha\alpha’} \int\!\!\!\int \chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* H_{12} \chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 &\ = E s_{\alpha_1\alpha_2} \\
a_{\alpha_1\alpha_2} (E_1 + E_2)
+\sum_{\alpha,\alpha’}a_{\alpha\alpha’}\int\!\!\!\int \chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* H_{12} \chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 &\ = E a_{\alpha_1\alpha_2}
\end{align}

となるね。これらは $s_{\alpha_1\alpha_2}$ $a_{\alpha_1\alpha_2}$ に関する連立方程式になるので、あとは数値計算でこれらの値を計算するだけだね。ちなみに対称と反対称のペアの積分は次の通りゼロだね。

\begin{align}
\int\!\!\!\int \chi^{S}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* H_{12}
\chi^{A}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 &\ = 0 \\
\int\!\!\!\int \chi^{A}_{\alpha_1\alpha_2}(\boldsymbol{r}_1, \boldsymbol{r}_2)^* H_{12}
\chi^{S}_{\alpha\alpha’}(\boldsymbol{r}_1, \boldsymbol{r}_2)dV_1dV_2 &\ = 0
\end{align}

次回、ヘリウム原子のエネルギー準位の計算結果を示すよ。