タグ: 量子井戸

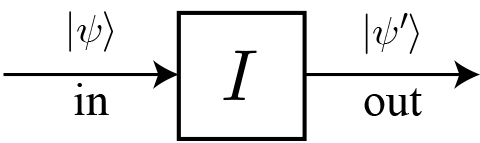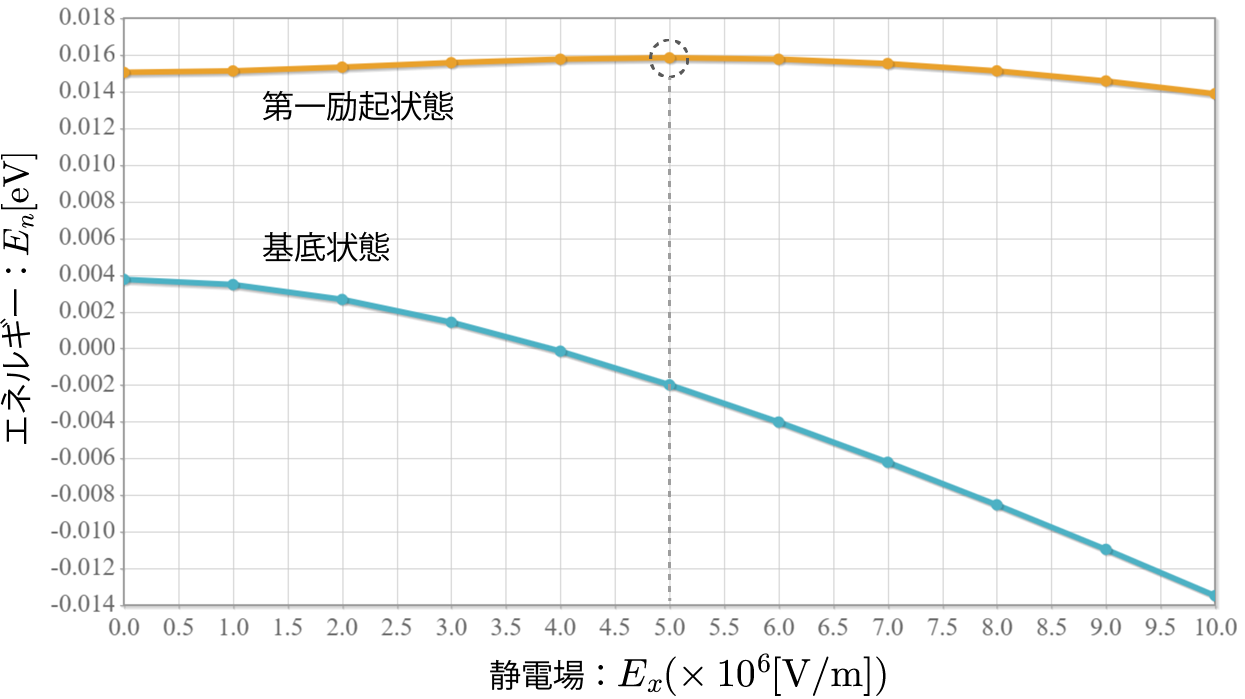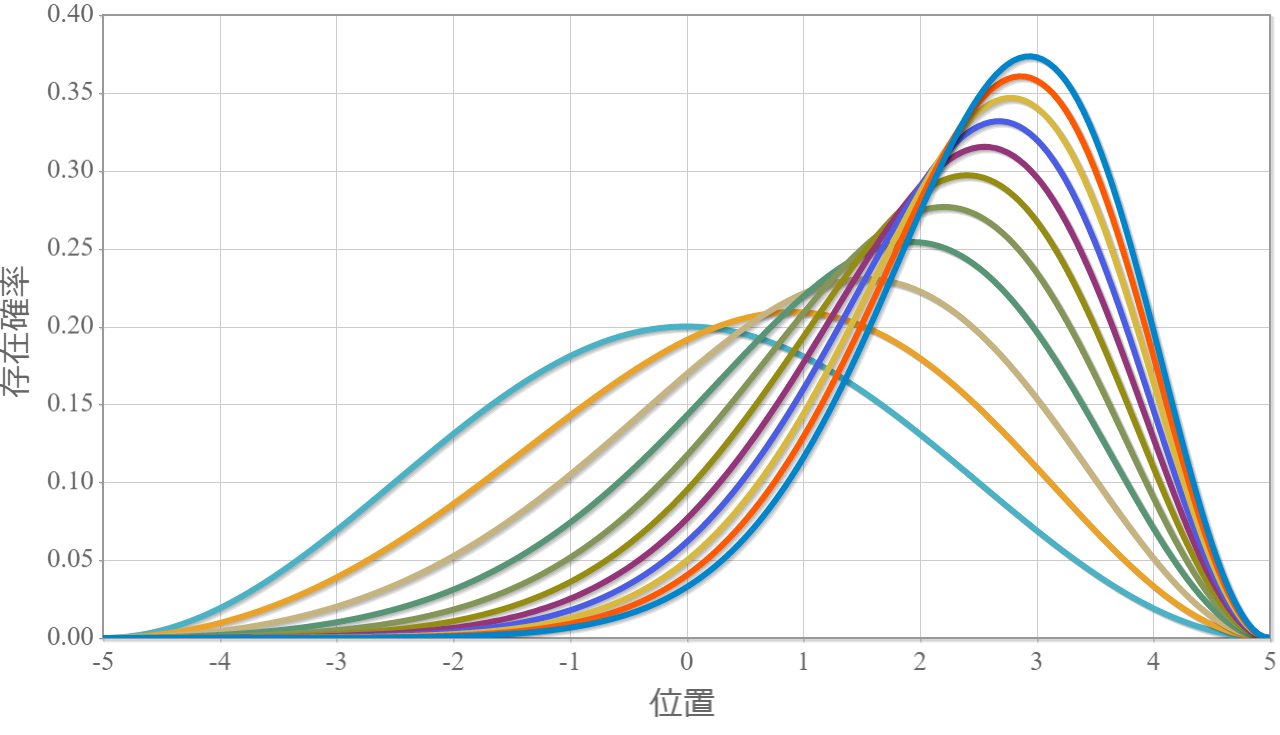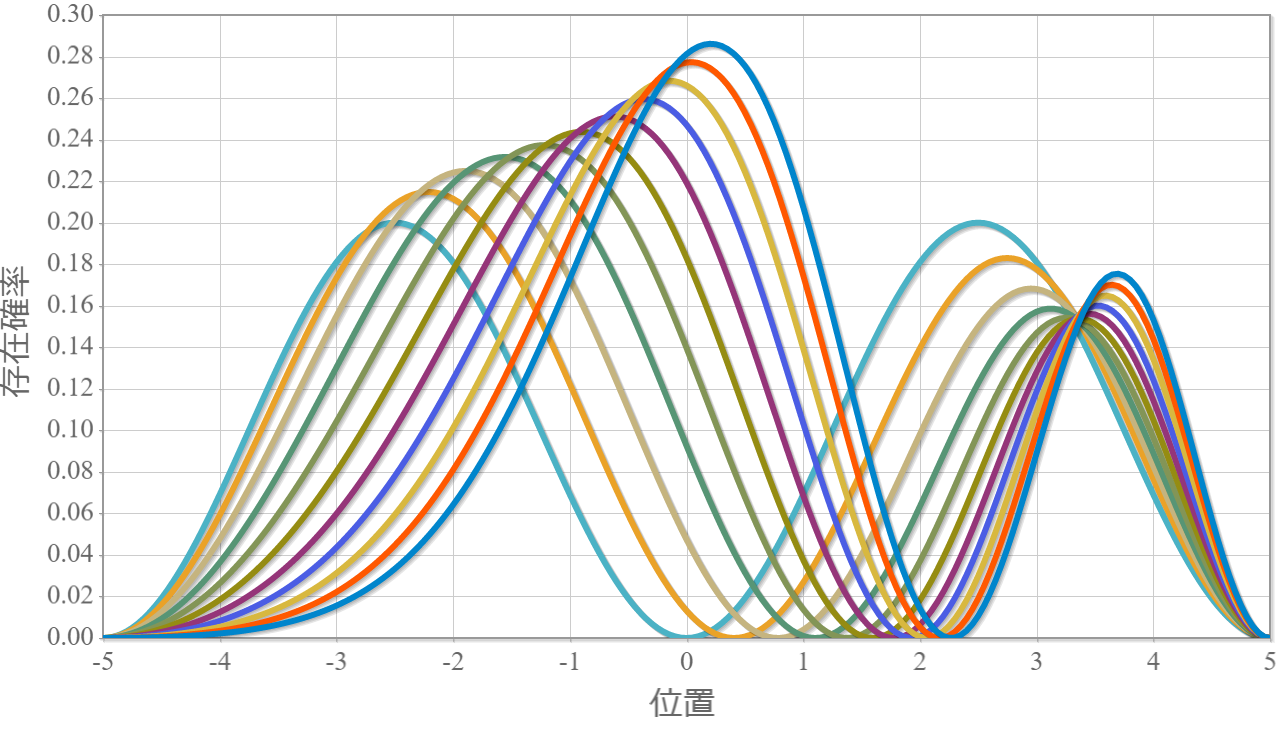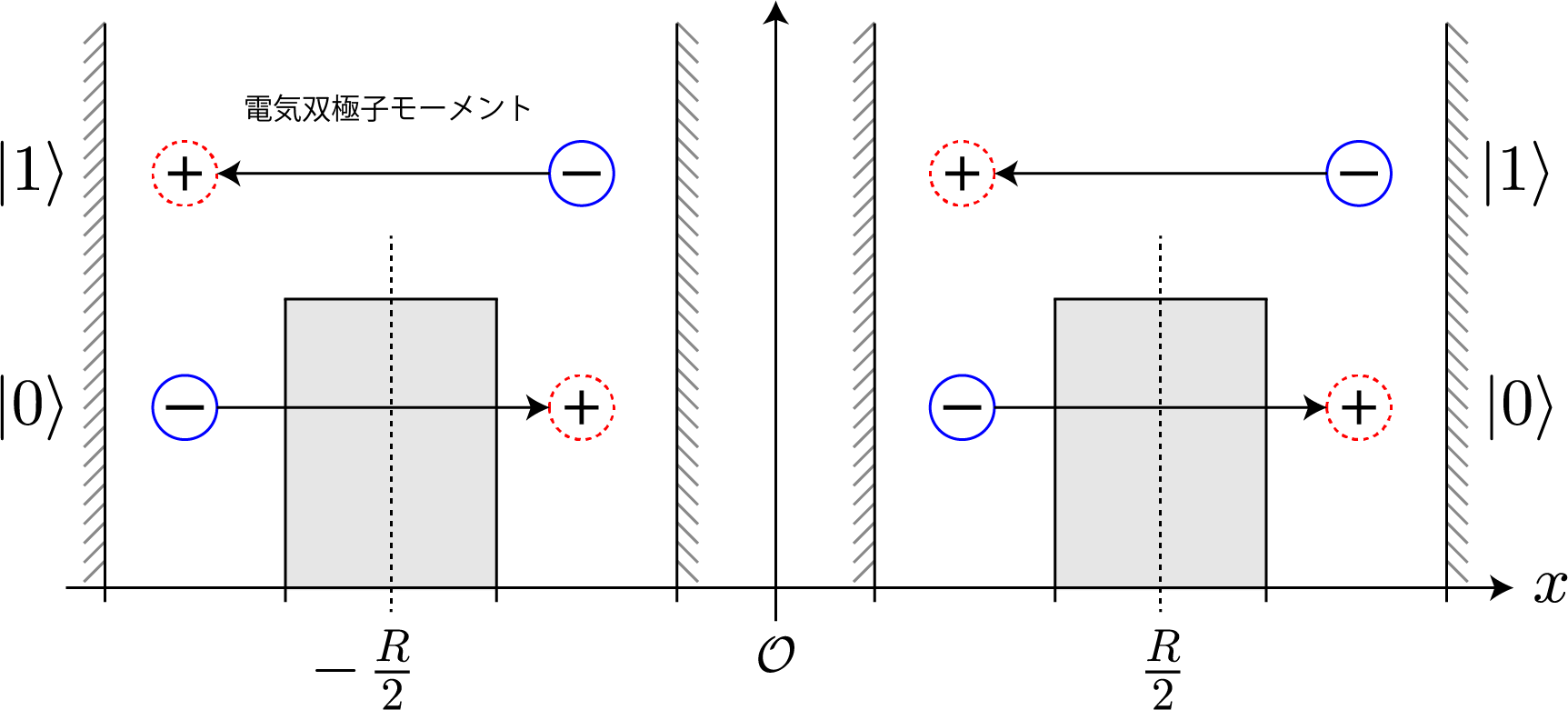
前回までで、１量子ビットを表現する量子井戸に束縛された電子の振る舞いを大体シミュレーションすることができたね。今回は、この量子井戸を２つ並べて２量子ビットとして利用するための表現方法と、２量子ビットの万能量子ゲートとして動作させるための動作原理についてまとめるよ。２量子ビットの表現を考える前にちょっと電磁気学の復習するよ。１つの量子ドットに束縛された電子に外部からx軸方向に静電場を加えた場合、電子が基底状態（$| 0\rangle$）に存在する場合には電子は左に分布し、励起状態（$| 1\rangle$）に存在する場合には電子は右に分布するんだったね（参照：（10）２重量子ドットに束縛された電子に静電場を加えたときの固有状態の計算結果）。この電子分布の偏りは第１次近似として次式で定義される電気双極子モーメント

\begin{align}
\boldsymbol{p}_E^{(1)} \equiv \int \boldsymbol{r}_1 \rho(\boldsymbol{r}_1) d\boldsymbol{r}_1 = \left\{ \matrix{ +\boldsymbol{p}_E & \cdots |0\rangle \cr -\boldsymbol{p}_E & \cdots|1\rangle }\right.
\end{align}

で表すことができるね。電気双極子モーメントは基底状態の場合は電気双極子が正の方向、励起状態の場合には負の方向に向くね。２つ目の量子井戸でも同様に

\begin{align}
\boldsymbol{p}_E^{(2)} &\ \equiv \int \boldsymbol{r}_2 \rho(\boldsymbol{r}_2) d\boldsymbol{r}_2 = \left\{ \matrix{ +\boldsymbol{p}_E & \cdots |0\rangle \cr -\boldsymbol{p}_E & \cdots|1\rangle }\right.
\end{align}

と表すことができるね。一般に２つの電気双極子モーメントが存在する場合、片方からもう片方への位置ベクトルを $\boldsymbol{R}$ として、相互作用によるポテンシャルエネルギーは

\begin{align}
U_E(\boldsymbol{R}) = \frac{1}{4\pi \epsilon_0}\, \frac{\boldsymbol{p}_E^{(1)}\cdot\boldsymbol{p}_E^{(2)}}{R^3} – \frac{3}{4\pi \epsilon_0}\, \frac{(\boldsymbol{p}_E^{(1)}\cdot\boldsymbol{R}) (\boldsymbol{p}_E^{(2)}\cdot\boldsymbol{R})}{R^5}
\end{align}

となるね。今回のように $\boldsymbol{R}$ の方向と電気双極子モーメントの向きが一直線の場合、

\begin{align}
U_E(R) = -\frac{1}{2\pi \epsilon_0}\, \frac{p_E^{(1)}p_E^{(2)}}{R^3} \equiv \mp \Delta U
\end{align}

となるので、電気双極子モーメントの向きが平行の場合には一致する場合にはエネルギーは $\Delta U$ 下がり、反対に向きが反平行の場合にエネルギーは $\Delta U$ 上がるね。この事実を用いて２量子ビットの量子ゲートを設計することができよ。

２量子ビットの量子状態の表現

１量子ビットの場合、量子井戸の基底状態と励起状態の固有関数の具体的な関数形は考えずに、それぞれケットを用いて $|0\rangle$ , $|1\rangle$ と表せることをはすでに解説したね。２量子ビットの場合、１つ目の「0」or「1」を第１量子ビットの状態、２つ目の「0」or「1」を第２量子ビットの状態として、$|0\rangle \otimes |0\rangle$ , $|0\rangle \otimes |1\rangle$ , $|1\rangle \otimes |0\rangle$ , $|1\rangle \otimes |1\rangle$ と表すことができるよ。「$\otimes$」は数学的には直積と呼ばれ、「$\otimes$」の前後の異なる座標系の状態をつなぐ役割を果たすよ。なお、「$\otimes$」を毎回書くのが煩わしい場合は、「$\otimes$」を省略して、$|00\rangle$, $|01\rangle$, $|10\rangle$, $|11\rangle$ とも表すよ。

電気双極子モーメント演算子と相互作用演算子

先に解説したとおり、量子井戸の基底状態と励起状態のどちらに存在するかによって、電気双極子モーメントの向きが異なるね。状態 $|0\rangle$ と $|1\rangle$ に作用する電気双極子モーメント演算子 $\hat{\boldsymbol{p}}_E$ を次のように定義するよ。

\begin{align}
\hat{\boldsymbol{p}}_E |0\rangle &\ = +\boldsymbol{p}_E |0\rangle \\
\hat{\boldsymbol{p}}_E |1\rangle &\ = -\boldsymbol{p}_E |1\rangle
\end{align}

この電気双極子モーメント演算子は２つの量子井戸の電子それぞれ個別に作用するので、先の２量子ビットの量子状態の表現を用いると

\begin{align}
\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E |00\rangle &\ = +\boldsymbol{p}_E^2 |00\rangle \\
\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E |01\rangle &\ = -\boldsymbol{p}_E^2 |01\rangle \\
\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E |10\rangle &\ = -\boldsymbol{p}_E^2 |10\rangle \\
\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E |11\rangle &\ = +\boldsymbol{p}_E^2 |11\rangle \\
\end{align}

と計算することができるよ。つまり、電気双極子モーメント同士の相互作用を表す演算子 $V_E$は

\begin{align}
V_E = -\frac{1}{2\pi \epsilon_0}\, \frac{\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E}{R^3}
\end{align}

と表すことができるね。

２量子ビットのハミルトニアン

電気双極子モーメントの相互作用演算子を定義できたので、あとはそれぞれの量子井戸の電子単体のハミルトニアンを考えるだけだね。$\hat{H}_1$ と $\hat{H}_2$ はそれぞれの量子井戸中の電子に静電場が加えられたときのハミルトニアンとして、第１量子ビットと第２量子ビットの基底状態エネルギーをそれぞれ $E_1^{(0)}$ と $E_2^{(0)}$、励起状態のエネルギーをそれぞれ $E_1^{(1)}$ と $E_2^{(1)}$ と表した場合、次のような固有状態とあらすことができるね。

\begin{align}
(\hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 ) |00\rangle &\ = (E_1^{(0)} + E_2^{(0)}) |00\rangle\\
(\hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 ) |10\rangle &\ = (E_1^{(1)} + E_2^{(0)}) |10\rangle\\
(\hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 ) |01\rangle &\ = (E_1^{(0)} + E_2^{(1)}) |01\rangle\\
(\hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 ) |11\rangle &\ = (E_1^{(1)} + E_2^{(1)}) |11\rangle
\end{align}

このハミルトニアンに先の電気双極子モーメントの相互作用演算子を加えると、ハミルトニアン $\hat {H}$ が完成するね。

\begin{align}
\hat {H} &\ = \hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes\hat{H}_2 + \hat{V}_E \\
\hat{V}_E &\ = -\frac{1}{2\pi \epsilon_0}\, \frac{\hat{\boldsymbol{p}}_E \otimes \hat{\boldsymbol{p}}_E}{R^3}
\end{align}

２量子ビットの量子状態はこのハミルトニアンの固有状態となっているよ。

\begin{align}
\hat {H} |00\rangle &\ = (E_1^{(0)} + E_2^{(0)} – \Delta U_E) |00\rangle\\
\hat {H} |10\rangle &\ = (E_1^{(1)} + E_2^{(0)} + \Delta U_E) |10\rangle\\
\hat {H} |01\rangle &\ = (E_1^{(0)} + E_2^{(1)} + \Delta U_E) |01\rangle\\
\hat {H} |11\rangle &\ = (E_1^{(1)} + E_2^{(1)} – \Delta U_E) |11\rangle
\end{align}

２量子ビット万能量子ゲートについて

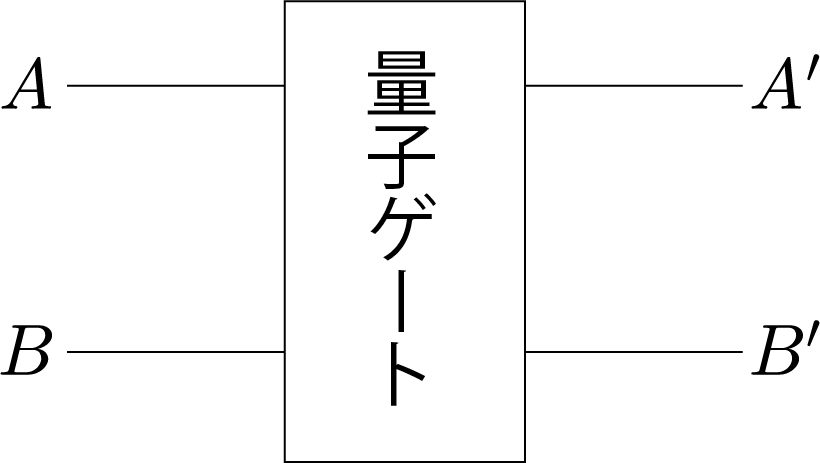
２量子ビット量子ゲートとは、２つの量子ビットの状態を入力とし、変化した２つの量子ビットの状態を出力とみなす素子を抽象化した表現だよ。右図のAとBが入力前の量子ビットの状態を表していて、A’とB’が変化後の量子ビットの状態を表しているよ。A, B, A’, B’ はそれぞれ $|0\rangle$ と $|1\rangle$ の任意の重ね合わせで与えられるよ。このような２量子ビット量子ゲートで最も重要なのは、A, B, A’, B’ の関係が下の真理値表で表される「制御・NOT演算（CNOT）ゲート」と呼ばれる量子ゲートだよ。

A	B
0	0
0	1
1	0
1	1

A’	B’
0	0
0	1
1	1
1	0

制御・NOT演算ゲートは、入力Aが $0$ の場合はBには何の変化もなく、入力 A が $1$ の場合は入力された B のビットを反転（NOT演算）させるよ。論理式で表すと

\begin{align}
A’&\ =A\\
B’&\ = A \otimes B
\end{align}

となるよ。この場合の「$\otimes$」は排他的論理和を表す記号で、先の直積とは違う意味だよ。そして実は、制御・NOT演算ゲートは複数組み合わせることで２量子ビットで構成される論理ゲートをすべて表現することができるんだよ！そのため、制御・NOT演算ゲートは２量子ビットの万能量子ゲートとも呼ばれるよ。２量子ビットの状態をケットベクトル

\begin{align}
|00\rangle = \left( \matrix{ 1\cr 0 \cr 0 \cr 0} \right) , |01\rangle = \left( \matrix{ 0\cr 1 \cr 0 \cr 0} \right), |10\rangle = \left( \matrix{ 0\cr 0 \cr 1 \cr 0} \right) , |11\rangle = \left( \matrix{ 0\cr 0 \cr 0 \cr 1} \right)
\end{align}

で表した場合、制御・NOT演算ゲート（CNOT）は

\begin{align}
{ \rm CNOT} = \left( \matrix{ 1& 0& 0&0 \cr 0&1 &0 & 0 \cr 0 & 0 & 0 & 1 \cr 0 & 0 &1& 0} \right)
\end{align}

と表すことができるね。実際に上記の真理値表を満たしていることが確認できるね。

\begin{align}
{\rm CNOT} |00\rangle &\ = |00\rangle\\
{\rm CNOT} |01\rangle &\ = |01\rangle\\
{\rm CNOT} |10\rangle &\ = |11\rangle\\
{\rm CNOT} |11\rangle &\ = |10\rangle\\
\end{align}

制御・NOT演算ゲートの動作原理

次に２量子ビット万能量子ゲートである制御・NOT演算ゲートを、２つの量子井戸を用いて具体的にどのようにして作ることができるのか解説するよ。本稿の前半で示したとおり、静電場が加えられた量子井戸中の電子は、基底状態（$|0\rangle$）と励起状態（$|1\rangle$）で異なる向きの電気双極子モーメントをもつので、相互作用の結果、第１量子井戸の電子状態が $|0\rangle$ か $|1\rangle$ によって、第２量子井戸の基底状態のと励起状態のエネルギー準位は変化するね。具体的には、第１量子井戸の電子状態が $|0\rangle$ の場合には第２量子井戸のエネルギーギャップは広がり、反対に第１量子井戸の電子状態が $|1\rangle$ の場合には第２量子井戸のエネルギーギャップは狭まるね。次の図はその模式図だよ。

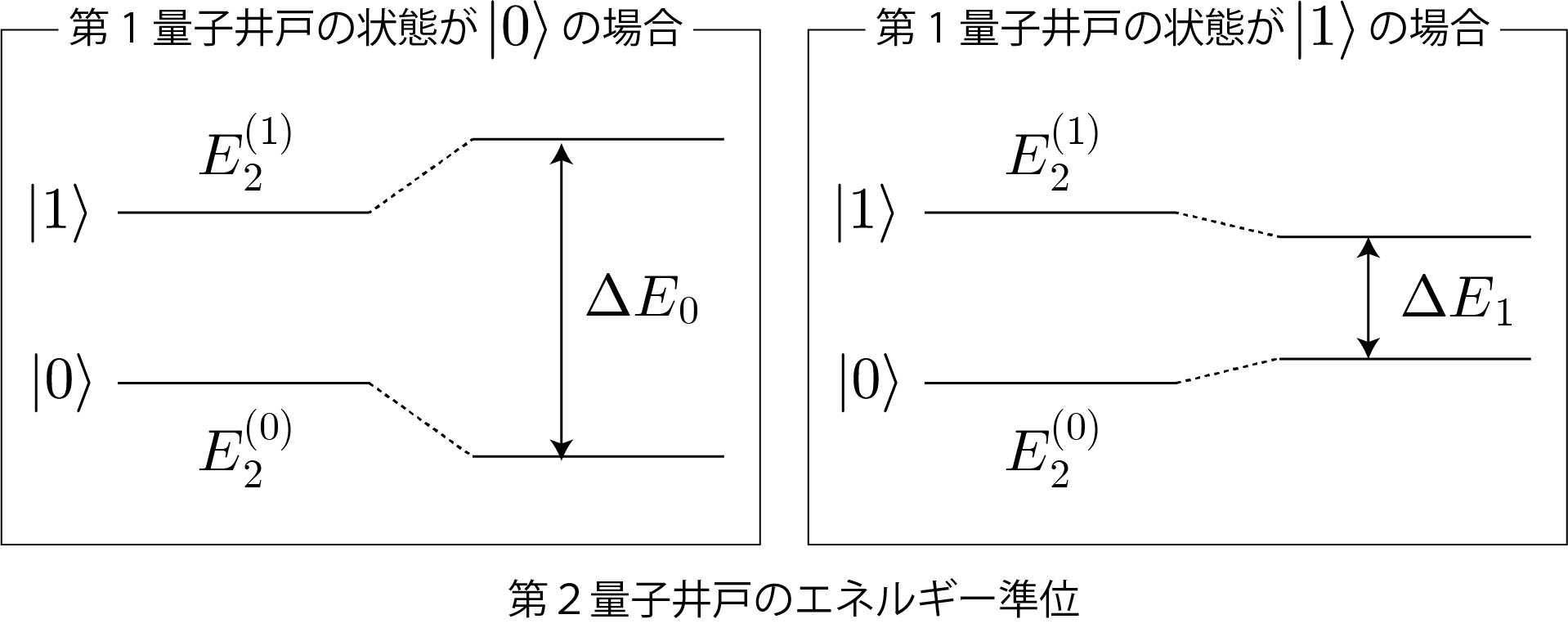
一方、エネルギーギャップに対応する電磁波を入射すると、これまでに何度か示したラビ振動を引き起こすことができるんだったね。つまり、狭まったエネルギーギャップ（$\Delta E_2$）に相当する電磁波を入射すると、第１量子井戸の電子状態が $|0\rangle$ の場合には変化しないけれども、第１量子井戸の電子状態が $|0\rangle$ の場合には第２量子井戸の状態をラビ振動させることができるので、入射時間を適切にコントロールすることで、制御・NOT演算ゲートと同じ動作をさせることができるね。

制御・NOT演算ゲートに対応するハミルトニアンと計算方法

以上から２つの量子井戸に束縛された電子を量子ビットとして用いた場合の制御・NOT演算ゲートに対応するハミルトニアンは次のような式に与えられる。

\begin{align}
\hat{H} = \hat{H}_1 \otimes \boldsymbol{1} + \boldsymbol{1} \otimes \hat{H}_2 + \hat{V}_E + \boldsymbol{1} \otimes \hat{V}_A(t)
\end{align}

$\hat{H}_1$ と $\hat{H}_2$ は電子の運動エネルギーと外部静電場によるポテンシャル項をあわせたもの、$\hat{V}_E$ は電気双極子モーメントによる相互作用項、$\hat{V}_A(t)$ は第２量子井戸に入射する電磁波との相互作用項だよ。この内、時間に依存する項は最後の $\hat{V}_A(t)$ だけだね。実際にシミュレーションするには、任意の状態 $\psi(t)\langle$ を

\begin{align}
|\psi(t)\rangle = a_{00}(t)|00\rangle + a_{01}(t)|01\rangle + a_{10}(t)|10\rangle + a_{11}(t)|11\rangle \equiv \sum\limits_{n=0} a_n (t) |n\rangle
\end{align}

と展開しておいて、時間に依存するシュレーディンガー方程式

\begin{align}
i\hbar \frac{d}{dt}|\psi(t)\rangle = \hat{H}|\psi(t)\rangle
\end{align}

に代入して、左から $\langle m |$ を掛けて得られる連立微分方程式

\begin{align}
i\hbar \frac{d a_{m}(t)}{dt} \, = \sum\limits_{n=0} \langle m |\hat{H}|n\rangle a_n(t)
\end{align}

を計算すればいいね。次回は実際に計算を行うけれども、その前に上記のハミルトニアンは重要な近似がなされているのがちょっと気になるね。というのも、２つの電子同士の相互作用を電気双極子モーメントの相互作用だけを取り込んでいる点が不満だね。やはりできるだけ第一原理的にやりたいので、$V_E$ をクーロンポテンシャル

\begin{align}
\hat{V}_E = \frac{1}{4\pi \epsilon_0}\, \frac{1}{|x_1 – x_2|}
\end{align}

として、まずは２つの量子井戸の電子相互作用を踏まえた固有状態を計算してみるね。

今回から２量子ビットを作るための方法を考えていくね。本稿ではその第一歩として１個の量子ドットに２個の電子を投入したときの固有状態を計算するための計算方法を解説するよ。電子のようにスピンが1/2の粒子が複数個存在する場合、スピン座標を含めて波動関数の座標を交換すると反対称（符号が反転）することが知られているよ（ディラック方程式より）。スピンが1/2の電子のような粒子は、スピン演算子の特定成分の固有値が $\pm\hbar/2$ の２つのなるので、$+$ 符号を上向き、$-$ 符号を下向きと表すことが多いいね。２個の粒子のスピンが同じ向き（平行スピン）の場合には波動関数全体で反平行になる必要があるので空間部分は反対称になるのに対して、２個の粒子のスピンが反対向き（反平行スピン）の場合には空間部分は対称になる必要があるね。１粒子の波動関数をこれまでと同じ

\begin{align}
\varphi_n(x) = \sqrt{\frac{2}{L}} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ E^{(0)}_n = \frac{\hbar^2 k_n^2}{2m_e} \ , \ k_n = \frac{\pi(n+1)}{L}
\end{align}

と表した場合、２個の電子の空間対称関数（$\varphi^{(S)}$）と空間反対称関数（$\varphi^{(A)}$）は２つの電子位置を $x_1$ と $x_2$ として、それぞれ次のように表されるよ。

\begin{align}
\varphi^{(S)}_{n_1n_2}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1}(x_1)\varphi_{n_2}(x_2) + \varphi_{n_1}(x_2)\varphi_{n_2}(x_1) \right]\\
\varphi^{(A)}_{n_1n_2}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1}(x_1)\varphi_{n_2}(x_2) – \varphi_{n_1}(x_2)\varphi_{n_2}(x_1) \right]
\end{align}

空間対称関数の場合、$x_1$ と $x_2$ を入替えても変化しないのに対して、空間反対称関数の場合、座標を入替えると符号がマイナスになるね。ただし、$n_1 = n_2$ の場合、空間対称関数の場合の係数は $1$ とする必要があることと、反対称関数の場合には関数値が $0$ になることに注意が必要だね。もし２個の電子が相互作用をしない場合、基底状態は空間対称関数（反平行スピン）で $n_1=n_2=0$ の場合だね。

\begin{align}
\varphi^{(S)}_{00}(x_1,x_2) = \varphi_{0}(x_1)\varphi_{0}(x_2)
\end{align}

第一励起状態は空間反対称関数（平行スピン）で $n_1=1, n_2=0$ あるいは $n_1=0, n_2=1$ の場合だね。

\begin{align}
\varphi^{(A)}_{10}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{1}(x_1)\varphi_{0}(x_2) – \varphi_{0}(x_2)\varphi_{1}(x_1) \right]\\
\varphi^{(A)}_{01}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{0}(x_1)\varphi_{1}(x_2) – \varphi_{1}(x_2)\varphi_{0}(x_1) \right]
\end{align}

両者とも単に符号が反転しているだけなので、同じ関数を表しているよ。

電子間のクーロン力を考慮した場合のハミルトニアンと固有状態の計算方法

電子は同符号の電荷を持っているので互いに反発するね。そのため、基底状態は先に示したような簡単な形にはならないね。クーロン力を考慮した場合の２個の電子に対するハミルトニアンは次のとおりだよ。

\begin{align}
\hat{H} = \hat{H}_1 + \hat{H}_2 + V(|x_1-x_2|)= -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_1^2} -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_2^2} + \frac{1}{4\pi\epsilon_0} \, \frac{1}{|x_1 – x_2|}
\end{align}

前の２項はそれぞれの電子の運動エネルギー、最後の項は相互作用を表しているね。このハミルトニアンの固有関数を $\psi^{(S)}(x_1, x_2)$（空間対称関数）、$\psi^{(A)}(x_1, x_2)$（空間反対称関数）と表した場合のシュレディンガー方程式は

\begin{align}
\hat{H} \psi^{(S)}(x_1, x_2) &\ = E \psi^{(S)}(x_1, x_2) \\
\hat{H} \psi^{(A)}(x_1, x_2) &\ = E \psi^{(A)}(x_1, x_2)
\end{align}

だね。この $\psi(x_1, x_2)$ は正規直交系である $\varphi^{(S)}_{n_1n_2}$ あるいは $\varphi^{(A)}_{n_1n_2}$ で展開できるはずなので、次のように表すことができるよ。

\begin{align}
\psi^{(S)}(x_1, x_2) &\ = \sum\limits_{n_1,n_2} a_{n_1n_2}\, \varphi^{(S)}_{n_1n_2}(x_1, x_2) \\
\psi^{(A)}(x_1, x_2) &\ = \sum\limits_{n_1,n_2} a_{n_1n_2}\, \varphi^{(A)}_{n_1n_2}(x_1, x_2)
\end{align}

ちなみに空間対称関数と反対称関数は直交するため混じり合うことは無いよ。ここからはいつもの常套手段でいくよ。この固有関数をハミルトニアンに代入して、両辺に $\varphi^{(S)*}_{n_1n_2}(x_1, x_2)$ あるいは $\varphi^{(A)*}_{m_1m_2}(x_1, x_2)$ を掛け算して全空間で積分すると

\begin{align}
a_{m_1m_2} ( E_{n_1}^{(0)} + E_{n_2}^{(0)}) + \sum\limits_{n_1,n_2} \langle m_1m_2|V(|x_1-x_2|)| n_1 n_2 \rangle a_{n_1n_2} = E a_{m_1m_2}
\end{align}

となるね。これは展開係数 $a_{m_1m_2}$ についての連立方程式となっているよ。対称性と反対称性の違いはブラ・ケット表記で表した積分

\begin{align}
\langle m_1m_2|V(|x_1-x_2|)| n_1 n_2 \rangle a_{n_1n_2} \equiv \left\{ \matrix{ \int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^{(S)*}_{m_1m_2}(x_1, x_2) V(|x_1-x_2|) \varphi^{(S)}_{n_1n_2}(x_1, x_2)dx_1dx_2 \cr \int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^{(A)*}_{m_1m_2}(x_1, x_2) V(|x_1-x_2|) \varphi^{(A)}_{n_1n_2}(x_1, x_2)dx_1dx_2 } \right.
\end{align}

に違いが現れるね。次回は実際に固有状態を計算するよ。

追記：2019.07.16

同じ量子井戸に２個の電子を配置する場合、上記のような展開では積分が発散してしまうため、計算不能となってしまうね。発散を抑えられる正規直交展開にしないといけないけれども、どうしてもうまくいかないので、この方法は一度断念するね。

前回、各領域に分けて接続条件から固有状態を計算しようと考えたけれど、よく考えたらこの方法は考え方が間違っているね。特に、特定の壁の高さや幅でしか固有状態が存在しないって言う点は完全に間違いだね。「単一の波数だけで固有状態をなす」という意味では特定の壁の高さや幅でしか固有状態が存在しないというのは正しいけれども、てっきり解析的に固有状態が求まると思い込んでいたことが問題だったね。ということで、これまでと同様に、解を正規直交系で展開して固有値方程式を解く必要がありそうだね。

固有状態の計算方法

１次元井戸型ポテンシャルのハミルトニアンは

\begin{align}
\hat{H} = -\frac{\hbar^2}{2m_e}\, \frac{d^2}{d x^2} + V(x)
\end{align}

で表されるね。$V(x)$ は以下のとおりだよ。

\begin{align}
V(x) = \left\{ \matrix{ \infty & x \leq -\frac{L}{2} \cr 0 & -\frac{L}{2} \leq x\leq -\frac{W}{2} \cr V & -\frac{W}{2} \leq x\leq \frac{W}{2} \cr 0 & \frac{W}{2} \leq x\leq \frac{L}{2} \cr \infty & \frac{L}{2} \leq x} \right.
\end{align}

このハミルトニアンの固有状態 $\bar{\varphi}(x)$ を、真ん中に壁が存在しない場合の固有関数

\begin{align}
\varphi_n(x) = \sqrt{\frac{2}{L}}\sin\left[ k_n \left( x + \frac{L}{2}\right)\right] \ , \ k_n = \frac{\pi(n+1)}{2}
\end{align}

で

\begin{align}
\bar{\varphi}(x) = \sum\limits_{n=0} a_0 \varphi_n(x)
\end{align}

と展開することを考えるよ。この固有関数をシュレーディンガー方程式 $\hat{H} \bar{\varphi}(x) = E\bar{\varphi}(x)$ に代入して、両辺に $\varphi_m(x)^*$ を掛けて全空間で積分するよ。これまでと同様、展開係数 $a_m$ についての連立方程式が導かれるね。

\begin{align}
E_m a_m + \sum\limits_{n=0}\langle m |V(x)| n \rangle a_n = E a_m
\end{align}

ただし、

\begin{align}
\langle m |V(x)| n \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi_m(x)^* V(x) \varphi_n(x) dx
\end{align}

だよ。次回は固有関数を計算してみるよ。

本シリーズは、右図のような量子ドットに束縛された電子の基底状態（固有関数：$\varphi_0(x)$、固有エネルギー：$E_0$）と第一励起状態（固有関数：$\varphi_1(x)$、固有エネルギー：$E_1$）の２準位を量子ビットとみなした計算機である、量子ドット量子コンピュータの動作をシミュレーションするよ。本稿では、この量子ドット型の量子ビットの表現と操作方法を解説するよ。

量子ドット型の量子ビットの表現

量子ドット型の量子ビットは、電子が基底状態に存在する状態と励起状態に存在する状態が重なり合った状態で表現されるよ。時間依存性まで考慮すると具体的には

\begin{align}
\psi(x,t) = a_0(t) \varphi_0(x) + a_1(t) \varphi_1(x)
\end{align}

と表されるね。$a_0(t)$ と $a_1(t)$ は基底状態と励起状態の重ね合わせの度合いを表わす複素数で、$|a_0(t)|^2$ と $|a_1(t)|^2$ がそれぞれの状態に存在する確率を表すよ。 この $a_0(t)$ と $a_1(t)$ は基底状態と励起状態はエネルギーから決まる角振動数 $\omega_0$ と $\omega_1$ で

\begin{align}
a_0(t) = a_0 e^{-i\omega_0 t} \ , \ a_1(t) = a_1 e^{-i\omega_1 t}
\end{align}

という感じで単振動しているよ。ちなみに各準位の角振動数はエネルギーと $\omega_0 = E_0 / \hbar$、 $\omega_1 = E_1 / \hbar$ の関係があるよ。基底状態と励起状態の角振動数が異なるので、時間が経過するに連れて位相差（位相比？）が生じるね。後で解説するけれども、

\begin{align}
\psi(x,t) = e^{-i\omega_0 t} \left[ a_0 \varphi_0(x) + a_1\varphi_1(x)e^{-i\omega_{01} t} \right]
\end{align}

この位相差の重要になるよ（$\omega_{01} \equiv \omega_{1}-\omega_{0} $）。上記の量子ビットの表記は、量子ドットの固有関数を用いているけれども、量子ビットそのものは様々な系で実現することができるので、一般的にはブラ・ケット表記を用いて、２つの量子状態を $| 0 \rangle , | 1 \rangle$ と抽象的に表現するね。これに倣えば、

\begin{align}
| \psi(t) \rangle = a_0 (t) | 0 \rangle + a_1 (t) | 1 \rangle
\end{align}

と表されるね。今後、量子ビットを表す場合にはこちらの表記を用いるよ。ちなみに、この $| 0 \rangle, | 1 \rangle$ と $\varphi_0(x), \varphi_1(x)$ とは $ \varphi_0(x) = \langle x | 0 \rangle , \varphi_1(x) = \langle x | 1 \rangle$ という関係があるよ。

１量子ビットの基本量子ゲート

量子ビットを制御するための操作は量子ゲートと呼ばれるよ。この量子ゲートは、量子力学的には量子状態に対してユニタリー変換を施すことに対応するよ。このユニタリ変換は、固有状態を縦ベクトルで表現したときに正方行列で表すことができるよ。$|0 \rangle$ と $|1 \rangle$ を要素数２個の縦ベクトル

\begin{align}
| 0 \rangle = \left( \matrix{ 1 \cr 0} \right) \ , \ | 1 \rangle = \left( \matrix{ 0 \cr 1} \right)
\end{align}

で表わすと、１量子ビットは

\begin{align}
| \psi \rangle = a_0 | 0 \rangle + a_1 | 1 \rangle = a_0 \left( \matrix{ 1 \cr 0} \right) + a_1 \left( \matrix{ 0 \cr 1} \right) = \left( \matrix{ a_0 \cr a_1} \right)
\end{align}

と表すことができて、ユニタリー変換はユニタリー行列と呼ばれる２×２の行列で表現ことができるよ。量子ゲートを表すユニタリー行列の例は次のとおりだよ。

恒等ゲート $I$

恒等ゲート $I$ は、入力状態と出力状態が同じとなる量子ゲートで、行列は単位行列で表されるよ。

\begin{align}
I = \left( \matrix{ 1 & 0 \cr 0 & 1} \right)
\end{align}

もちろん、量子ゲート通過後の状態 $| \psi’ \rangle$ は、通過前の状態 $| \psi \rangle$ と一致するよ。

\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \left( \matrix{ 1 & 0 \cr 0 & 1} \right) \left( \matrix{ a_0 \cr a_1} \right)= \left( \matrix{ a_0 \cr a_1} \right)
\end{align}

否定ゲート $X$

否定ゲート $X$ は、量子ビットの状態を反転させる量子ゲートで、行列は次のように表されるよ。

\begin{align}
X = \left( \matrix{ 0 & 1 \cr 1 & 0} \right)
\end{align}

次の計算でわかる通り、量子ゲートを通過すると行列要素が反転していることが分かるね。

\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \left( \matrix{ 0 & 1 \cr 1 & 0} \right)\left( \matrix{ a_0 \cr a_1} \right) = \left( \matrix{ a_1 \cr a_0} \right)
\end{align}

この量子ゲートは、外部から特定の振動数の電磁波を特定時間与えることで生じるエネルギー準位間の遷移で実現することができるよ。

位相シフトゲート $P_{\theta}$

位相シフトゲート $P_{\theta}$ は、量子ビットの２つの状態の相対的な位相をずらす量子ゲートで、行列は次のように表されるよ。

\begin{align}
P_{\theta} = \left( \matrix{ 1 & 0 \cr 0 & e^{i\theta}} \right)
\end{align}

次の計算でわかる通り、量子ゲートを通過すると $a_1$ に位相因子 $e^{i\theta}$ が掛かるよ。

\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \left( \matrix{ 1 & 0 \cr 0 & e^{i\theta}} \right) \left( \matrix{ a_0 \cr a_1} \right) =
\left( \matrix{ a_0 \cr a_1e^{i\theta}} \right)
\end{align}

この量子ゲートは、先に示したとおり、異なるエネルギー状態で振動数が違うことを考慮すると、特定時間だけ放っておくことで実現することができるよ。

アダマールゲート $H$

アダマールゲート $H$ は、量子ビットの回転を表す量子ゲートで、行列は次のように表されるよ。

\begin{align}
H = \frac{1}{\sqrt{2}} \left( \matrix{ 1 & 1 \cr 1 & -1 }\right)
\end{align}

次の計算でわかる通り、量子ゲートを通過すると、等しい重みで混合されるよ。$H^2 = I$ となるので、アダマールゲートは2回通すと元にもどるね。

\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \frac{1}{\sqrt{2}} \left( \matrix{ 1 & 1 \cr 1 & -1 }\right) \left( \matrix{ a_0 \cr a_1} \right) =\frac{1}{\sqrt{2}} \left( \matrix{ a_0 + a_1 \cr a_0 – a_1} \right)
\end{align}

このゲートの重要性を示す一例として、入力状態が $a_0 = 1 , a_1 =0$ （100% $| 0 \rangle$ 状態 ）とすると、

\begin{align}
\left( \matrix{ a_0′ \cr a_1′} \right) = \frac{1}{\sqrt{2}} \left( \matrix{ 1 & 1 \cr 1 & -1 }\right) \left( \matrix{
1 \cr 0} \right) =\frac{1}{\sqrt{2}} \left( \matrix{ 1 \cr 1} \right)
\end{align}

となり、均等に混合した状態（$| 0 \rangle$ と $| 1 \rangle$ が50%ずつの状態 ）を作り出すことができるね。
なお、この量子ゲートも外部からの特定の振動数の電磁波を特定時間与えることで生じるエネルギー準位間の遷移で実現することができるよ。

1量子ビットの万能量子ゲート

まず、任意の１量子ビットの状態は

\begin{align}
| \psi \rangle = e^{i\gamma } \left[ \cos\frac{\theta}{2} | 0 \rangle + \sin\frac{\theta}{2} e^{i\phi} | 1 \rangle \right]
\end{align}

で表されることが知られているよ（$ 0 \leq \theta \leq \pi \ , \ 0 \leq \phi \leq 2\pi $）。ただし、全体に掛かる因子 $e^{i\gamma}$ は観測には掛からないので無視できるので、

\begin{align}
| \psi \rangle = \cos\frac{\theta}{2} | 0 \rangle + \sin\frac{\theta}{2} e^{i\phi} | 1 \rangle
\end{align}

ですべての状態を表しているよ。この状態を生み出すことのできる量子ゲートは「1量子ビットの万能量子ゲート」と呼ばれるよ。このゲートはアダマールゲート $H$ と 位相シフトゲート $P_{\theta}$ の２つを組み合わせることで作ることができるよ。例えば、初期状態として $ | \psi \rangle =| 0 \rangle $ から任意の状態を生成するには、

\begin{align}
U = P_{\phi+\frac{\pi}{2}} H P_{\theta} H
\end{align}

という演算で実現することができるよ。実際に確かめてみよう。

\begin{align}
| \psi’ \rangle &\ = P_{\phi+\frac{\pi}{2}} H P_{\theta} H | 0 \rangle = P_{\phi+\frac{\pi}{2}} H P_{\theta} \frac{ | 0 \rangle + | 1 \rangle }{\sqrt{2}} = P_{\phi+\frac{\pi}{2}} H \frac{ | 0 \rangle + e^{i\theta}| 1 \rangle }{\sqrt{2}}\\
&\ = P_{\phi+\frac{\pi}{2}} \frac{ (1+e^{i\theta})| 0 \rangle + (1-e^{i\theta})| 1 \rangle }{2} = \frac{ (1+e^{i\theta})| 0 \rangle + (1-e^{i\theta}) e^{i\phi+i\frac{\pi}{2}}| 1 \rangle }{2}\\
&\ = e^{i\frac{\theta}{2}} \frac{ (e^{-i\frac{\theta}{2}}+e^{i\frac{\theta}{2}})| 0 \rangle + i(e^{-i\frac{\theta}{2}}-e^{i\frac{\theta}{2}}) e^{i\phi}| 1 \rangle }{2} \\
&\ = e^{i\frac{\theta}{2}}\left[ \cos\frac{\theta}{2} | 0 \rangle+ \sin\frac{\theta}{2} e^{i\phi}| 1 \rangle \right]
\end{align}

ちゃんとなってるね。以上で１量子ビットについての解説は終わりだよ。まだ１量子ビットなのでこれ単体ではコンピュータとして何の演算もできないね。２量子ビットについての解説は、１量子ビットの物理的操作方法をマスターした後に改めて解説するよ。

前回、定式化した量子ドットに束縛された電子に電磁波を加えたときの計算結果を示すよ。量子井戸の横幅は $L = 10 \times 10^9 [{\rm m}]$（ $=10[{\rm nn}]$ ）としているよ。 次の図は、基底状態１００％の初期状態の電子に、第一励起状態と基底状態のエネルギー差の電磁波を入射したときの時間依存性だよ。想定通り、ラビ振動として知られる２つの準位間をsin関数的に振動する様子がわかるね。

基底状態１００％から励起状態１００％まで遷移する時間間隔の電磁波パルスは、πパルスと呼ばれるよ。量子コンピュータの量子ビットを入れ替えるのに利用されるね。次回は、静電場を加えた電子に対して、ラビ振動をちゃんと起こせるかをチェックするよ。

今度は静電場の代わりに、量子ドットに束縛された電子に電磁波（直線偏光）を外部から与えて、基底状態と第一励起状態との間のラビ振動を確認するよ。電磁波を表すベクトルポテンシャルを $\boldsymbol{A}$ とした場合のハミルトニアンは次のとおりだね（参考）。

\begin{align}
\hat{H} = \hat{H}_0 + \hat{V}(t) = -\frac{\hbar^2}{2m_e} \frac{d^2}{dx^2} + \frac{e}{m_e} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}
\end{align}

今回は１次元系で考えているので、ベクトルポテンシャルを $\boldsymbol{A}(t) = (A_x(t), 0, 0)$ として、

\begin{align}
A_x(t) = A_0 \cos(kx-\omega t)
\end{align}

と考えるよ。そして、このハミルトニアンの固有関数を外場が無いときの固有関数

\begin{align}
\varphi_n(x) = \sqrt{\frac{2}{L}} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ E_n = \frac{\hbar^2 k_n^2}{2m_e} \ , \
k_n = \frac{\pi(n+1)}{L}
\end{align}

で展開して、その係数の値が時間に依存するとして展開するよ。

\begin{align}
\psi(x, t) = \sum\limits_{n=0} a_n(t) \varphi_n(x)
\end{align}

これを時間依存を考慮したシュレーディンガー方程式

\begin{align}
i \hbar \frac{\partial }{\partial t} \psi(x, t) = \hat{H} \psi(x, t)
\end{align}

に代入して、両辺に $\varphi^*_m(x)$ を掛けて全空間で積分するよ。すると、$a_m(t)$ に関する連立常微分方程式が得られるね。

\begin{align}
i \hbar \frac{d a_m(t)}{d t} = E^{(0)}_m a_m(t) + \sum\limits_{n=0} \langle m | \hat{V}(t) | n \rangle a_n(t)
\end{align}

$\langle m | \hat{V}(t) | n \rangle$ は、$\hat{p}_x/m_e = [\hat{H}_0, x ]/i\hbar$ を考慮すると

\begin{align}
\langle m | \hat{V}(t) | n \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_m(x) \hat{V}(t)
\varphi_n(x)\, dx = \frac{eA_0}{m_e} \langle m | \cos(kx-\omega t) p_x | n \rangle = \frac{eA_0}{i\hbar} \langle m | \cos(kx-\omega t) [\hat{H}_0, x ] | n \rangle
\end{align}

と変形できて、波長が量子ドットのサイズよりも十分大きいと仮定すると、$kx \simeq 0$ と近似することができるので

\begin{align}
\langle m | \hat{V}(t) | n \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) \left[ E^{(0)}_m – E^{(0)}_n \right] \langle m |
x | n \rangle
\end{align}

となるので、$a_m(t)$ に関する連立常微分方程式は

\begin{align}
i \hbar \frac{d a_m(t)}{d t} = E^{(0)}_m a_m(t) + \frac{eA_0}{i\hbar} \cos(\omega t)\sum\limits_{n=0} \left[ E^{(0)}_m – E^{(0)}_n \right] \langle m | x | n \rangle a_n(t)
\end{align}

となるね。$\langle m |x | n \rangle $ は時間に依存しないので、一度計算するだけでいいね。電磁波の角振動数が２準位間のエネルギー差 $\Delta E$ と表して $\omega = \Delta E / \hbar$ となるときに、２準位間を周期的に遷移するね。次回はこれをシミュレーションするよ。

前回、定式化した量子ドットに束縛された電子に静電場を加えたときの固有状態の計算結果を示すよ。量子井戸の横幅は $L = 10 \times 10^9 [{\rm m}]$（ $=10[{\rm nn}]$ ）としているよ。

基底状態と第一励起状態の固有エネルギーの静電場の強度依存性

次のグラフは基底状態と第一励起状態の固有エネルギーの静電場の強度依存性だよ。基底状態は電場強度が強くなるにつれてエネルギーが下がっているのに対して、第一励起状態は電場強度が強くなるにつれて初めエネルギーが上がっていった後に下がって行く様子がわかるね。その分岐点となる電場強度はおおよそ $E_x = 5.0\times 10^6 [{\rm V/m}]$ であることがわかるね。静電場が加わることでエネルギーが上下する理由は電気双極子が誘起されていることを意味しているよ。エネルギーが下がるのは電気双極子モーメントが静電場の向きと平行となり、反対に上がるのは電気双極子モーメントが静電場の向きと反平行となっていると考えられるね。

基底状態と第一励起状態の固有関数の静電場強度別の空間依存性

次のグラフは基底状態の固有関数の静電場強度別の空間依存性だよ（$E_x = 0.0\times 10^6 \sim 1.0\times 10^6 [{\rm V/m}]$）。静電場が強くなるほど電子の分布がx軸の正方向に偏っていくね。つまり、電気双極子モーメントが大きくなっていることに対応しているよ。

次のグラフは第一励起状態の固有関数の静電場強度別の空間依存性だよ（$E_x = 0.0\times 10^6 \sim 10.0\times 10^6 [{\rm V/m}]$）。第一励起状態はエネルギー準位の電場強度依存性からも分かる通り、$E_x = 5.0\times 10^6 [{\rm V/m}]$ までは、電場強度に応じて電子分布はx軸の負方向に偏っていくね。それよりも大きな電場を加えると、反対にx軸の正方向に偏っていくね。

以上の結果より、外部から静電場を加えることで、基底状態と第一励起状態は異なる向きの電気双極子モーメントが誘起されることがわかったね（シュタルク効果）。これを利用することで、基底状態と第一励起状態の区別をつけることができるよ。次回は、この基底状態と第一励起状態を入れ替えるラビ振動を確かめるよ。

　量子コンピュータを勉強のために、シミュレーションが一番簡単そうな量子ドットに束縛された電子のエネルギー準位を量子ビットとして扱うタイプを念頭に置いて、量子コンピュータを実現するために必要な素子の具体的な物理系のシミュレーション（数値実験）を行っていくよ。今回は、１次元版量子ドット（井戸型ポテンシャル）に束縛された電子の状態を変化させるために静電場を加えたときの固有状態を調べるよ。

静電場を加えたハミルトニアンとシュレディンガー方程式

井戸型ポテンシャルに束縛された電子に外部からx軸方向の静電場 $E_x$ を加えると、電子は静電場によって空間分布が変化することが考えられるね。量子井戸の底のポテンシャルエネルギーを０としたときのハミルトニアンは次のとおりだね。

\begin{align}
\hat{H} = \hat{H}_0 + \hat{V} = -\frac{\hbar^2}{2m_e} \frac{d^2}{dx^2} – e E_x x \\
\end{align}

$\hat{V}$ は静電場によるポテンシャルエネルギーだよ。$\hat{H}_0$ は 外場無し（$E_x = 0$）のときのハミルトニアンで、井戸の深さが無限大のときには固有関数 $\varphi_n(x)$ を用いて、エネルギー固有状態 $\hat{H}_0 \varphi_n(x) = E_n \varphi_n(x)$ を満たすよ。固有関数と固有エネルギーは

\begin{align}
\varphi_n(x) = \sqrt{\frac{2}{L}} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ E_n = \frac{\hbar^2 k_n^2}{2m_e} \ , \ k_n = \frac{\pi(n+1)}{L}
\end{align}

だね。$k_n$ は波数だよ。静磁場が加わったときの固有関数と固有エネルギーをそれぞれ $\varphi(x)$ と $E$ と表したとき、シュレディンガー方程式は

\begin{align}
\hat{H} \varphi(x)= E \varphi(x) \\
\end{align}

となるけれど、この $\varphi(x)$ を $\varphi_n(x)$ を用いて

\begin{align}
\varphi(x) = \sum\limits_{n=0} a_n \varphi_n(x)
\end{align}

と展開して、固有関数と固有エネルギーを計算するよ。

固有関数と固有エネルギーの計算方法

シュレディンガー方程式の両辺に $\varphi^*_m(x)$ を掛けて全空間で積分するよ。固有関数の直交関係を考慮すると、シュレディンガー方程式は

\begin{align}
E^{(0)}_m a_m + \sum\limits_{n=0} \langle m | \hat{V} | n \rangle a_n = E a_m
\end{align}

という展開係数 $ a_n $ に関する連立方程式になるね。ただし、$\langle m | \hat{V} | n \rangle $ は

\begin{align}
\langle m | \hat{V} | n \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_m(x) \hat{V} \varphi_n(x)\, dx
\end{align}

だよ。連立方程式は行列で表すとわかりやすくなるので、エネルギーの小さい順に固有関数の係数を並べると次のようになるよ。

\begin{align}
\left(\matrix{ E^{(0)}_0 +\langle 0 | \hat{V} | 0 \rangle & \langle 1 | \hat{V} | 0 \rangle & \langle 2 | \hat{V} | 0 \rangle & \langle 3 | \hat{V} | 0 \rangle & \langle 4 | \hat{V} | 0 \rangle & \cdots \cr
\langle 0 | \hat{V} | 1 \rangle & E^{(0)}_1 + \langle 1 | \hat{V} | 1 \rangle & \langle 1 | \hat{V} | 2 \rangle & \langle 1 | \hat{V} | 3 \rangle &\langle 1 | \hat{V} | 4 \rangle &\cdots \cr
\langle 0 | \hat{V} | 2 \rangle & \langle 1 | \hat{V} | 2 \rangle & E^{(0)}_2 + \langle 2 | \hat{V} | 2 \rangle & \langle 3 | \hat{V} | 2 \rangle& \langle 4 | \hat{V} | 2 \rangle& \cdots \cr
\langle 0 | \hat{V} | 3 \rangle & \langle 1 | \hat{V} | 3 \rangle & \langle 2 | \hat{V} | 3 \rangle & E^{(0)}_3 + \langle 3 | \hat{V} | 3 \rangle& \langle 4 | \hat{V} | 3 \rangle& \cdots \cr
\langle 0 | \hat{V} | 4 \rangle & \langle 1 | \hat{V} | 4 \rangle & \langle 2 | \hat{V} | 4 \rangle & \langle 3 | \hat{V} | 4 \rangle& E^{(0)}_4 + \langle 4 | \hat{V} | 4 \rangle& \cdots \cr
\vdots & \vdots & \vdots & \vdots & \vdots & \ddots } \right) \left(\matrix{ a_{0} \cr a_{1}\cr a_{2} \cr a_{3} \cr a_{4} \cr \vdots }\right) = E \left(\matrix{ a_{0} \cr a_{1}\cr a_{2} \cr a_{3} \cr a_{4} \cr \vdots }\right)
\end{align}

まさに行列表した固有値方程式の形になっているのがわかるね。 これで固有値と固有ベクトルを計算すると、固有値はそのまま外場が加えられた場合のエネルギー、固有ベクトルがそのまま展開係数の値そのものになるね。次回は、この計算結果を示すよ。