【動画】10日で作る量子ドットコンピュータ【3日目】量子井戸の電子状態の基礎実験2:静電場による電気分極
【量子コンピュータを作ろう!】(17)2つの独立した2重量子井戸に束縛された電子による制御NOT演算計算結果
今回は、前回示したハミルトニアン(クーロン相互作用+静電場+電磁波)を用いて計算した結果を示すよ。上左図は前々回に示したエネルギー準位の静電場強度依存性だけれども、$|10\rangle$ と $|11\rangle$ のエネルギー差に対応した電磁波を入射して生じる状態遷移を計算するよ。ちなみにこれは、第1量子ビットが $|1\rangle$ のときに第2量子ビットを反転させる制御・NOT演算に対応しているよ。あとで示すけれども、2量子ビットのラビ振動は量子ビット同士が絡み合った量子もつれ(エンタングル)状態を任意に生成することができるよ。
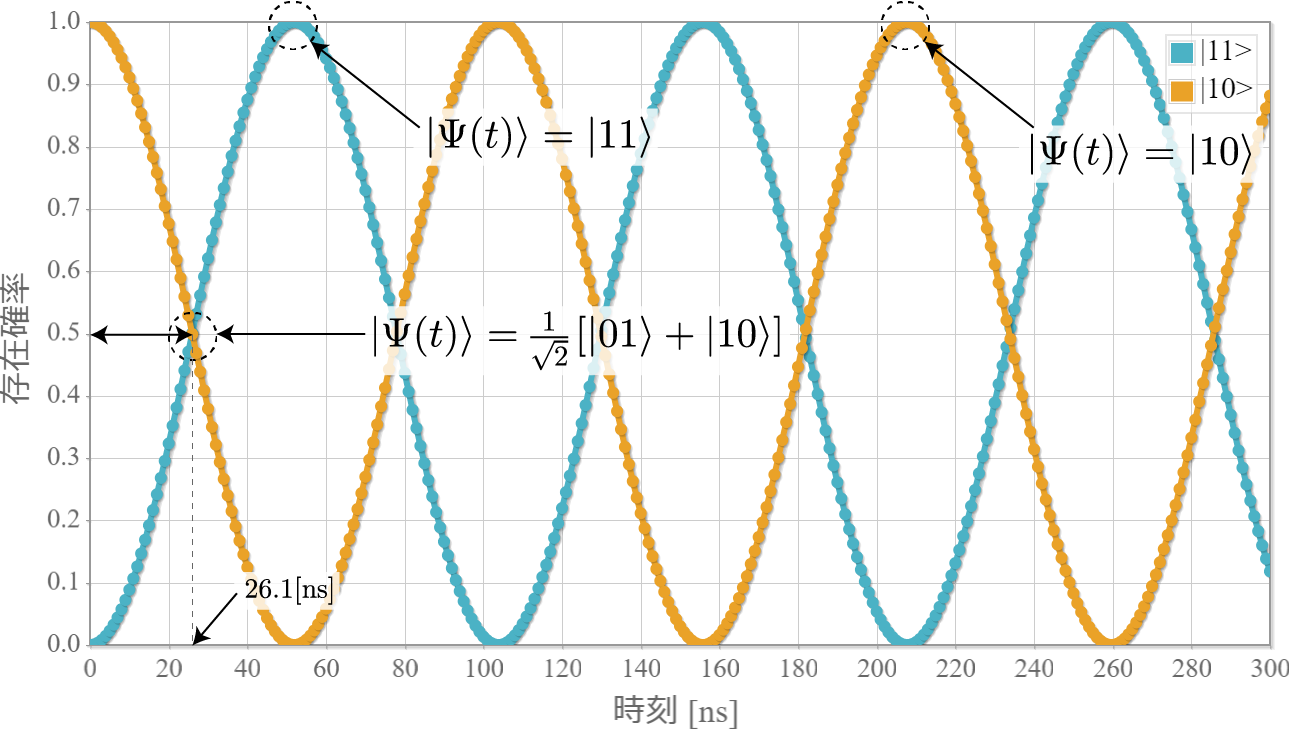
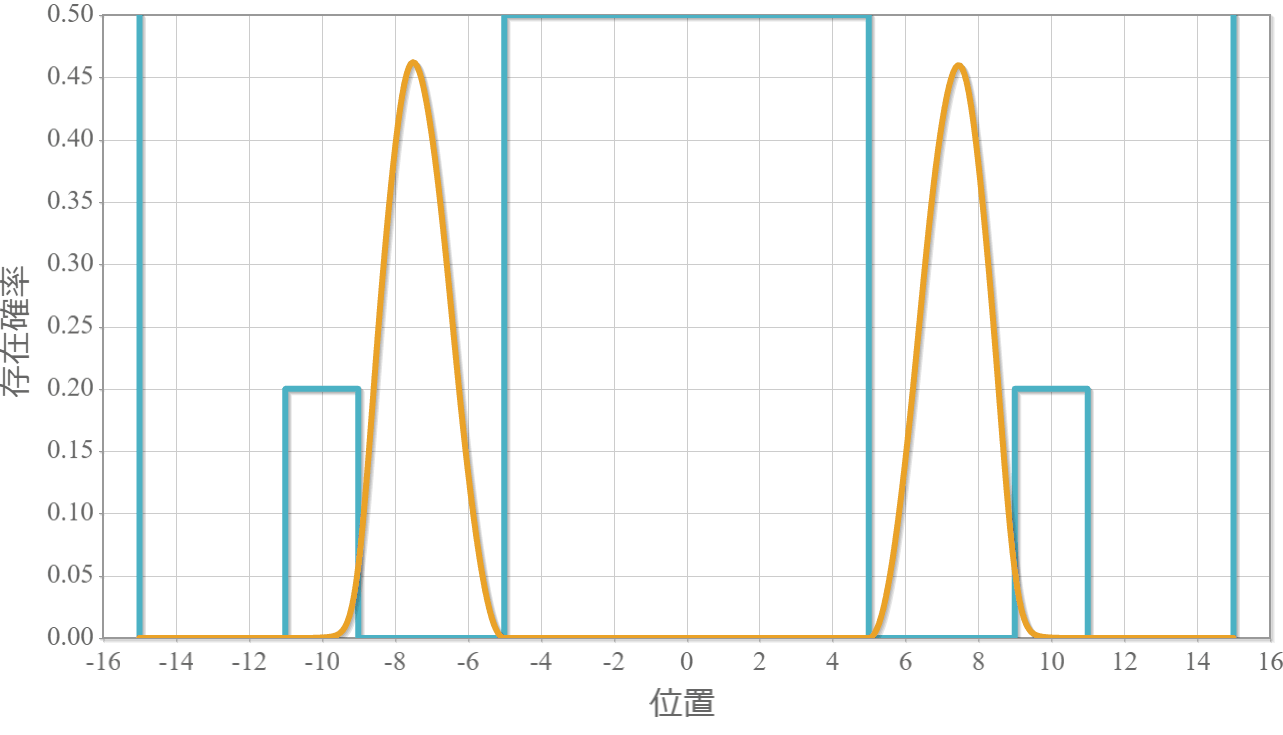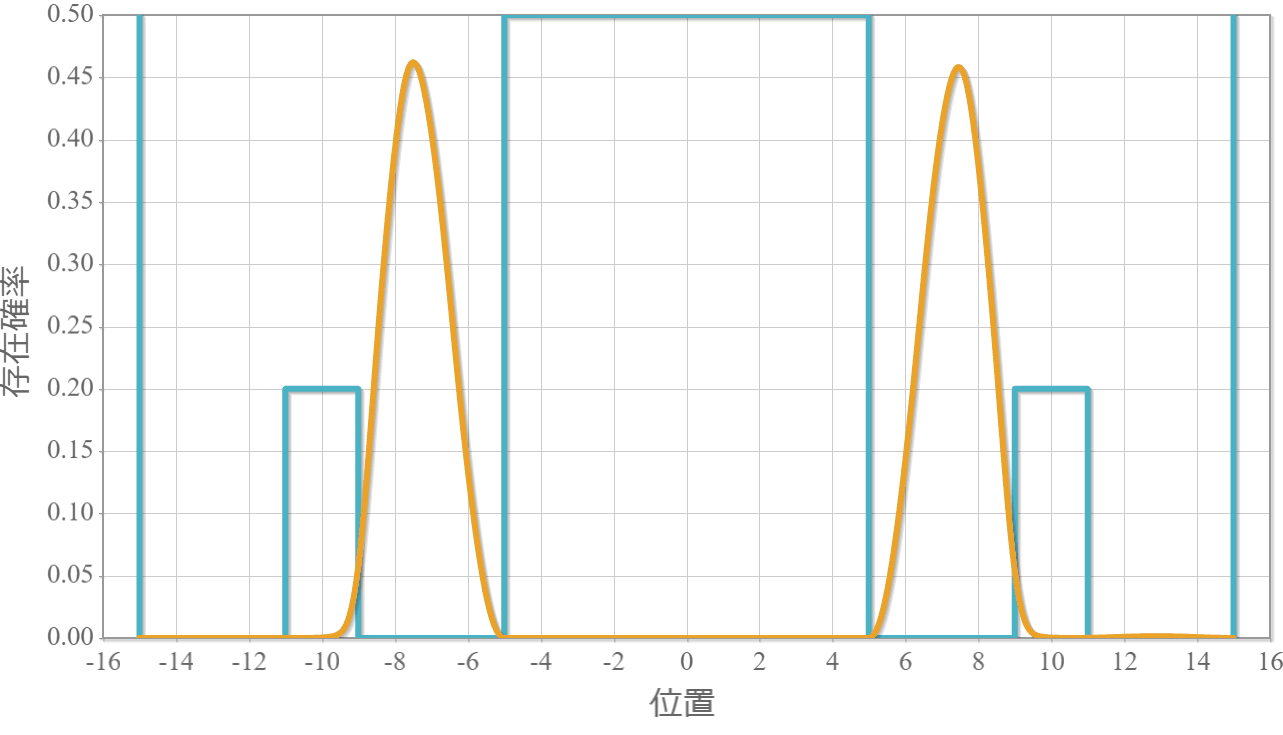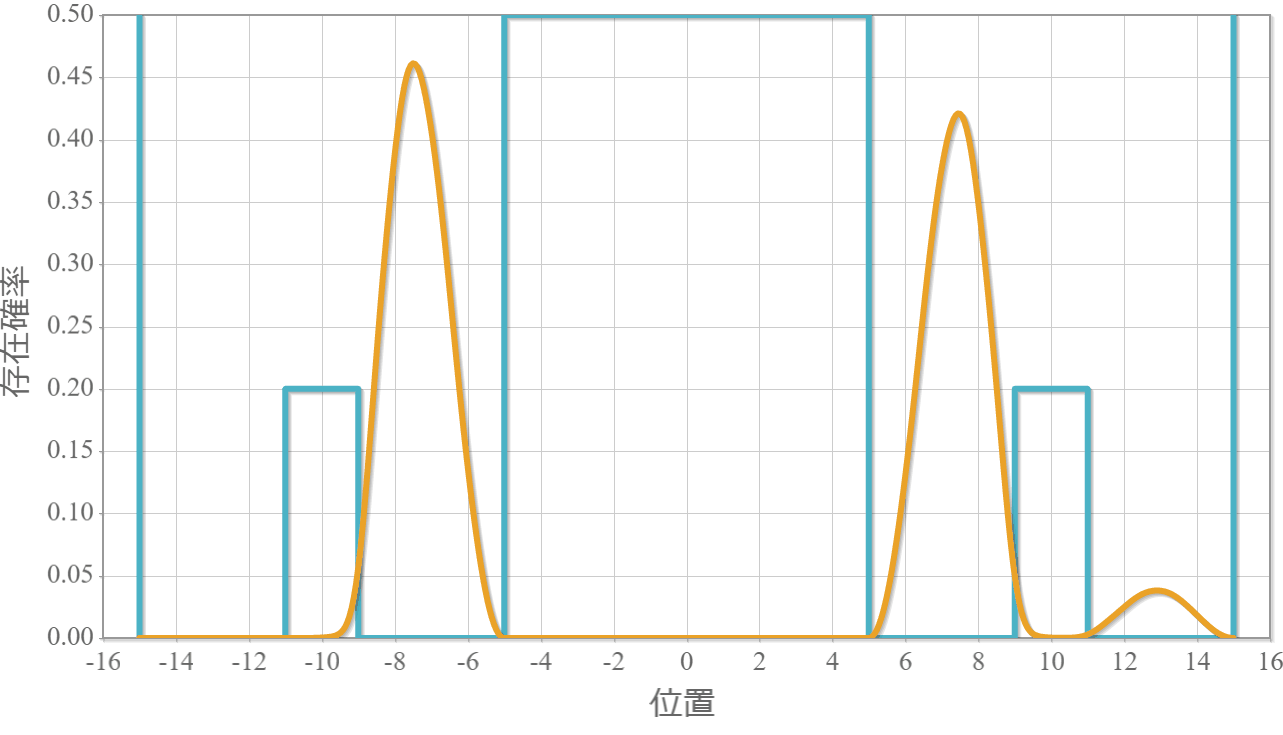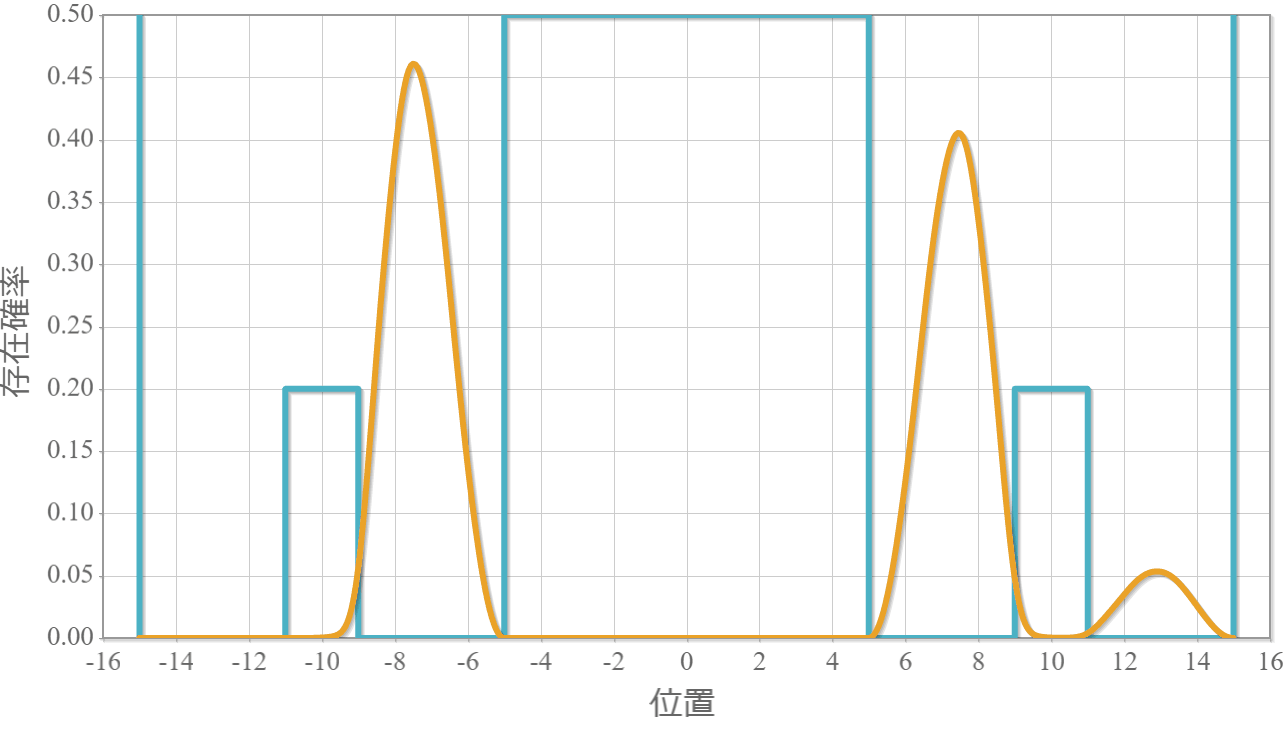
遷移状態:$|10\rangle$ と $|11\rangle$ の存在確率の時間依存性
次のグラフは初期状態 $|10\rangle$ に角振動数 $\omega = \Delta E /\hbar$ の電磁波を入射したときの、$|11\rangle$ との状態遷移の様子だよ。ラビ振動の結果、2つの状態を三角関数的に行ったり来たりするね。$|10\rangle$ 100%の初期状態に約 $ 26.1[{\rm ns}]$ 照射すると、$|10\rangle$ と $|11\rangle$ の存在確率は50%つづとなり、さらに約 $ 26.1[{\rm ns}]$ 照射すると、反対に $|11\rangle$ 100% の状態になるね。ちょうど存在確率が反転する時間の光は「$\pi$パルス」って呼ばれるよ。
先にも言ったけれども、このラビ振動は2量子ビット同士が絡み合った量子もつれ状態を生み出すことができるね。例えば、$|10\rangle$ と基底状態の $|01\rangle$ のエネルギー差 $\Delta E_{01}^{11}$ として、角振動数 $\omega = \Delta E_{01}^{11} /\hbar$ の電磁波を $\pi$パルスの半分を入射すると、
\begin{align}
|\Psi(t)\rangle = \frac{1}{\sqrt{2}} \left[ |10\rangle + |01\rangle \right]
\end{align}
という状態を作ることができるね。これは単に $|10\rangle$ と $|01\rangle $ の存在確率が 50%づつっていうだけでなくて、第1量子ビットを観測したときに、第2量子を観測しなくてもその状態が100%の確率で分かるという量子もつれ状態となっているよ。具体的には、第1量子ビットが $|0\rangle$ の場合には第2量子ビットは必ず $|1\rangle$ に存在し、また反対に第1量子ビットが $|1\rangle$ の場合には第2量子ビットは必ず $|0\rangle$ に存在するよ。ちなみに、この量子井戸の間隔を量子状態が変化しないようにゆっくりと、どこまで離していっても成り立つよ。そのため、通信に利用することができると考えられているよ。その場合は、量子井戸による量子もつれではなく、光子をを用いた量子もつれを利用するよ。
制御NOT演算に対応する波動関数の時間発展
次の図はラビ振動による制御NOT演算時の波動関数の時間経過を示したアニメーションだよ。左の第1量子井戸は電子が右側( $|1\rangle$ )、第2量子井戸は電子が左側( $|0\rangle$ )と右側( $|1\rangle$ )を行ったり来たりしているね。
これで量子コンピュータの2量子ビットマシンの動作原理シミュレーションは完成したよ。
【量子コンピュータを作ろう!】(16)2つの独立した2重量子井戸に束縛された電子による制御NOT演算のハミルトニアンと計算方法
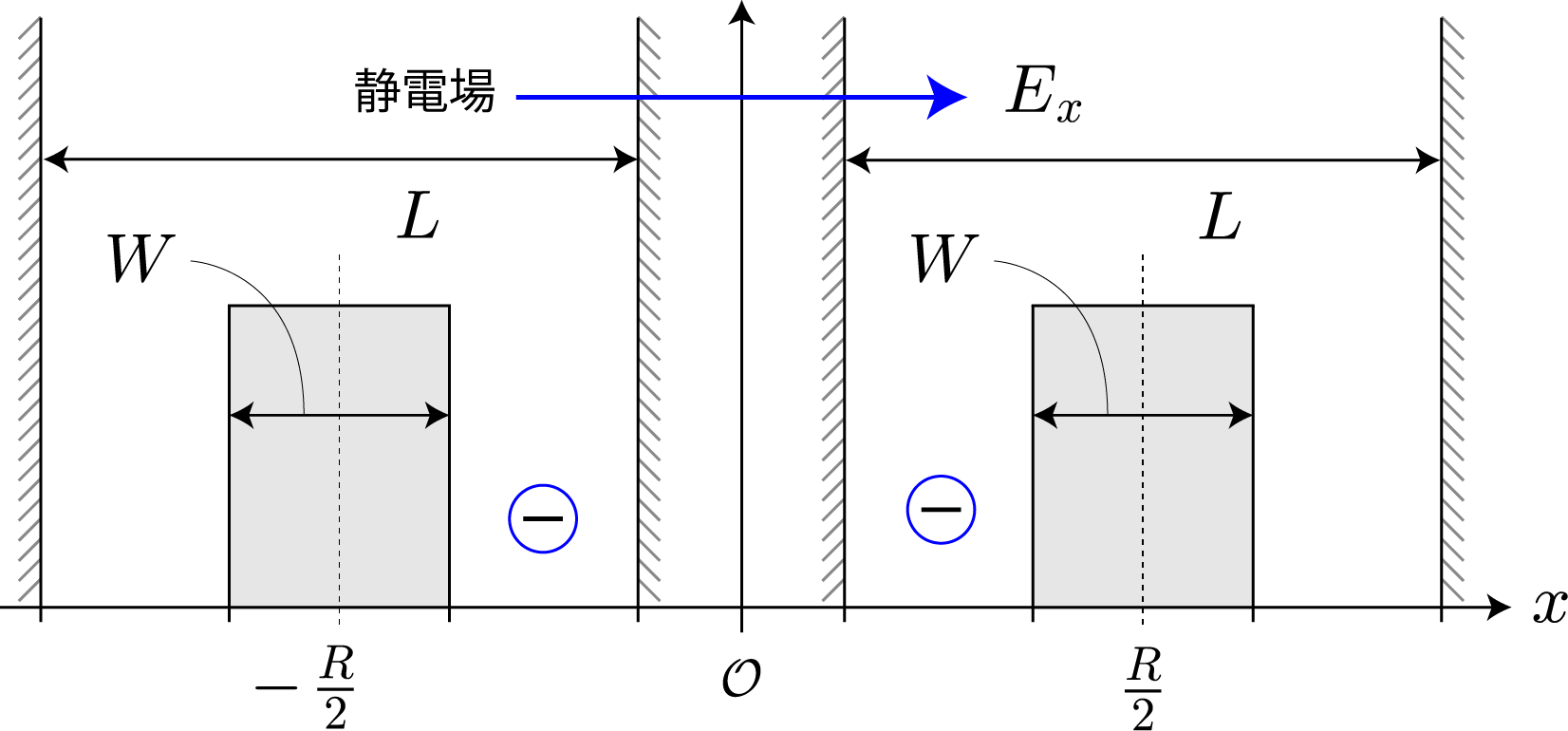
いよいよ最終目的の2量子ビットによる制御NOT演算を行うために、時間発展に必要なハミルトニアンの導出と計算方法を示すよ。復習から入っていくね。量子ビットを表す2つの量子井戸(幅:$L=10[{\rm nm}]$、高さ$+\infty$)はそれぞれが壁(幅: $W=L/5=2[{\rm nm}]$、高さ $V_0=0.3[{\rm eV}]$)で仕切られた2部屋になっていて、前々回と前回解説したとおり、2つの量子井戸の間隔 $R$ がちょうどよければ($R=20[{\rm nm}]$)、電子間のクーロン相互作用が存在しても、電子は左右のどちらかに存在する状態を作り出せるね。そして、それぞれの量子井戸で左側に電子が存在する状態を $|0\rangle$、右側に電子が存在する場合を $|1\rangle$ と表わして、2電子の状態は $|00\rangle$、$|01\rangle$、$|10\rangle$、$|11\rangle$ の4パターンで表すよ。
定常状態のハミルトニアンと固有関数
この系の固有関数は、2つの量子井戸でそれぞれ定義される関数
\begin{align}
\varphi_{n_1}(x_1) &\ = \sqrt{\frac{2}{L}}\sin\left[ k_{n_1} \left( x_1 + \frac{R}{2} + \frac{L}{2}\right)\right] \ , \
k_{n_1} = \frac{\pi(n_1+1)}{L} \\
\varphi_{n_2}(x_2) &\ = \sqrt{\frac{2}{L}}\sin\left[ k_{n_2} \left( x_2 – \frac{R}{2} + \frac{L}{2}\right)\right] \ , \
k_{n_2} = \frac{\pi(n_2+1)}{L} \\
\end{align}
を用いたその積
\begin{align}
\varphi_{n_1n_2}(x_1, x_2) = \varphi_{n_1}(x_1)\varphi_{n_2}(x_2)
\end{align}
で表される正規直交系で展開することができるね。ちなみに単純な積で表されるのは2つの電子は交わらないからだよ。この2電子系の正規直交関数を用いて、次のように展開することができるね。
\begin{align}
\psi_{l_1l_2}(x_1, x_2) = \sum\limits_{n_1n_2} a^{(l_1l_2)}_{n_1n_2} \varphi_{n_1n_2}(x_1, x_2)
\end{align}
$l_1$ と $l_2$ は $0$ または $1$ のどちらかを取り、$\psi_{00}(x_1, x_2)$ は $|00\rangle$、$\psi_{01}(x_1, x_2)$ は $|01\rangle$、$\psi_{10}(x_1, x_2)$ は $|10\rangle$、$\psi_{11}(x_1, x_2)$ は $|11\rangle$ にそれぞれ対応した固有関数だよ。$a^{(l_1l_2)}_{n_1n_2}$ のように上付きのインデックス $l_1, l_2$ をつけたのはそれぞれの状態で展開係数の値が異なるので明示的につけているよ。この固有関数に対応するハミルトニアンは次のとおりだよ。
\begin{align}
\hat{H}^{(0)} = -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_1^2} + eE_xx_1 + V_1(x_1)-\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_2^2} + eE_xx_2 + V_2(x_2) + \frac{e^2}{4\pi\epsilon_0}\,\frac{1}{|x_1-x_2|}
\end{align}
$\hat{H}^{(0)}$ とインデックスに $(0)$ をつけているのは、前回すでに固有状態を計算できていて、次はこれに電磁波を加えることを想定しているからだよ。先の固有関数はこのハミルトニアンなので固有状態は
\begin{align}
\hat{H}^{(0)}\psi_{l_1l_2}(x_1, x_2) = E^{(0)}_{l_1l_2}\psi_{l_1l_2}(x_1, x_2)
\end{align}
と表されるよ。ここまでが前回の内容だね。ちなみに固有状態は
\begin{align}
\hat{H}^{(0)}|l_1l_2\rangle &\ = E^{(0)}_{l_1l_2}|l_1l_2\rangle \\
\langle l_1l_2| \hat{H}^{(0)} &\ = \langle l_1l_2|E^{(0)}_{l_1l_2}
\end{align}
とも表すことができるよ。これは後で使うね。
電磁波を入射したときのハミルトニアンと計算方法

次に状態遷移を起こすために電磁波を加えるよ。ベクトルポテンシャルを $\boldsymbol{A}(t)$ としてハミルトニアンは
\begin{align}
\hat{H}(t) = \hat{H}^{(0)} + \frac{e}{m_e} \boldsymbol{A}(t)\cdot \hat{\boldsymbol{p}}_1 + \frac{e}{m_e} \boldsymbol{A}(t)\cdot \hat{\boldsymbol{p}}_2
\end{align}
となるね。今回も1次元系で考えているので、ベクトルポテンシャルを$\boldsymbol{A}(t) = (A_x(t), 0, 0)$ として、
\begin{align}
A_{x_1}(t) &\ = A_0 \cos(kx_1-\omega t)\\
A_{x_2}(t) &\ = A_0 \cos(kx_2-\omega t)
\end{align}
なので、ハミルトニアンは
\begin{align}
\hat{H}(t) = \hat{H}^{(0)} + \frac{e}{m_e} A_0 \left[ \cos(kx_1-\omega t)\hat{p}_{x_1} +\cos(kx_2-\omega t)\hat{p}_{x_2} \right]
\end{align}
となるね。このハミルトニアンは時間に依存するので固有状態は存在しないので、波動関数 $\Psi(t,x_1,x_2)$ を先の固有関数 $\psi_{l_1l_2}(x_1, x_2)$ で展開するよ。
\begin{align}
\Psi(t,x_1,x_2) = \sum\limits_{l_1 l_2} b_{l_1l_2}(t) \psi_{l_1l_2}(x_1, x_2)
\end{align}
$b_{l_1l_2}(t)$ が展開係数で、この展開係数が時間とともに変化するよ。時間に依存するシュレーディンガー方程式
\begin{align}
i\hbar \frac{\partial }{\partial t} \Psi(t,x_1,x_2)= \hat{H}(t) \Psi(t,x_1,x_2)
\end{align}
に代入して、両辺に $\psi_{m_1m_2}^*(x_1, x_2)$ を掛けて全空間で積分すると、次のような連立微分方程式になるよ。
\begin{align}
i\hbar \frac{d b_{m_1m_2}(t) }{d t} = E^{(0)}_{m_1m_2} b_{m_1m_2}(t) + e A_0 \sum\limits_{l_1 l_2} b_{l_1l_2}(t) \langle m_1 m_2| \left[\cos(kx_1-\omega t)\frac{\hat{p}_{x_1}}{m_e} + \cos(kx_2-\omega t)\frac{\hat{p}_{x_2}}{m_e}\right]| l_1l_2 \rangle
\end{align}
$\hat{p}_{x_1}/m_e = [\hat{H}^{(0)}, x_1 ]/i\hbar$、 $\hat{p}_{x_2}/m_e = [\hat{H}^{(0)}, x_2 ]/i\hbar$ の恒等式と長波長近似($kx_1 = kx_2 \simeq 0$)を考慮すると次のようになるよ(特に長波長近似を課すことをしなくても数値計算自体は問題なくできるよ。でも表式が簡単になるね)。
\begin{align}
&\ \langle m_1 m_2| \left[\cos(kx_1-\omega t)\frac{\hat{p}_{x_1}}{m_e} + \cos(kx_2-\omega t)\frac{\hat{p}_{x_2}}{m_e}\right]| l_1l_2 \rangle\\
&\ =\frac{1}{i\hbar} \langle m_1 m_2| \left[\cos(kx_1-\omega t)\left(\hat{H}^{(0)}x_1 – x_1\hat{H}^{(0)}\right) + \cos(kx_2-\omega t)\left(\hat{H}^{(0)}x_2- x_2\hat{H}^{(0)}\right)\right]| l_1l_2 \rangle\\
&\ \simeq \frac{1}{i\hbar}\cos(\omega t)\langle m_1 m_2| \left[\hat{H}^{(0)}x_1 – x_1\hat{H}^{(0)} + \hat{H}^{(0)}x_2- x_2\hat{H}^{(0)}\right]| l_1l_2 \rangle\\
&\ = \frac{1}{i\hbar}\cos(\omega t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right) \langle m_1 m_2|(x_1 + x_2)| l_1l_2
\rangle \\
&\ = \frac{1}{i\hbar}\cos(\omega t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right) \int_{-\frac{R}{2}-\frac{L}{2}}^{-\frac{R}{2}+\frac{L}{2}} dx_1\int_{\frac{R}{2}-\frac{L}{2}}^{\frac{R}{2}+\frac{L}{2}}dx_2 \psi_{m_1m_2}^*(x_1, x_2)(x_1 + x_2)\psi_{l_1l_2}(x_1, x_2)\\
&\ \equiv \frac{1}{i\hbar}\cos(\omega t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right) K^{m_1m_2}_{l_1l_2}
\end{align}
この $K^{m_1m_2}_{l_1l_2}$ は時間に依存しないので1度計算すれば良いね。この $K^{m_1m_2}_{l_1l_2}$ を用いると先の連立微分方程式は次のようになるよ。
\begin{align}
i\hbar \frac{d b_{m_1m_2}(t) }{d t} = E^{(0)}_{m_1m_2} b_{m_1m_2}(t) + \frac{e A_0}{i\hbar} \cos(\omega t) \sum\limits_{l_1 l_2} b_{l_1l_2}(t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right)K^{m_1m_2}_{l_1l_2}
\end{align}
電磁波の角振動数が2準位間のエネルギー差 $\Delta E = E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2}$ と表して $\omega = \Delta E / \hbar$ となるときに、2準位間を周期的に遷移するね。$\Delta E = E^{(0)}_{11} – E^{(0)}_{10}$ を与えることで、制御・NOT演算となることを次回シミュレーションするよ。
【量子コンピュータを作ろう!】(15)2つの独立した量子井戸に束縛された電子の基礎実験3:クーロン相互作用+静電場(2重量子井戸)

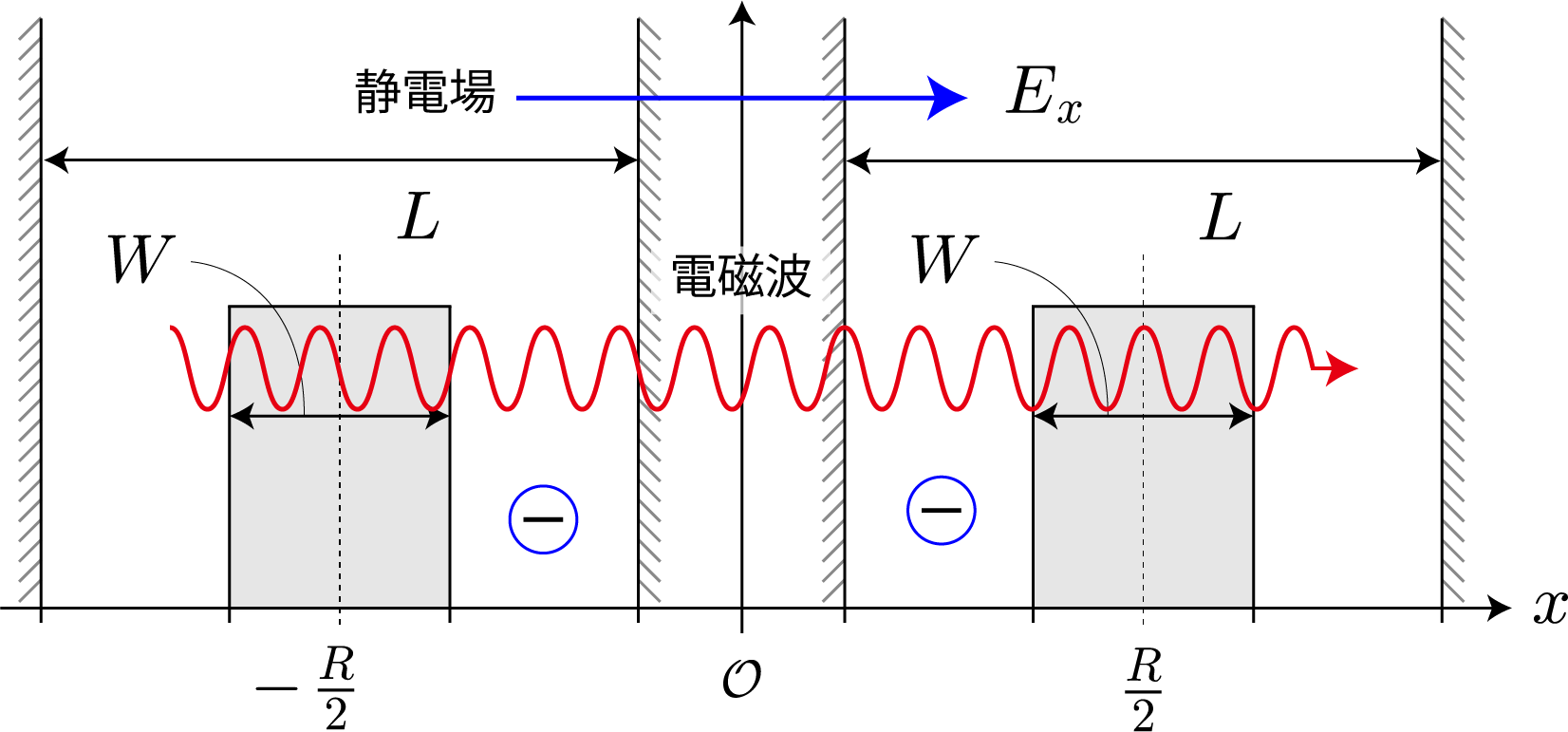
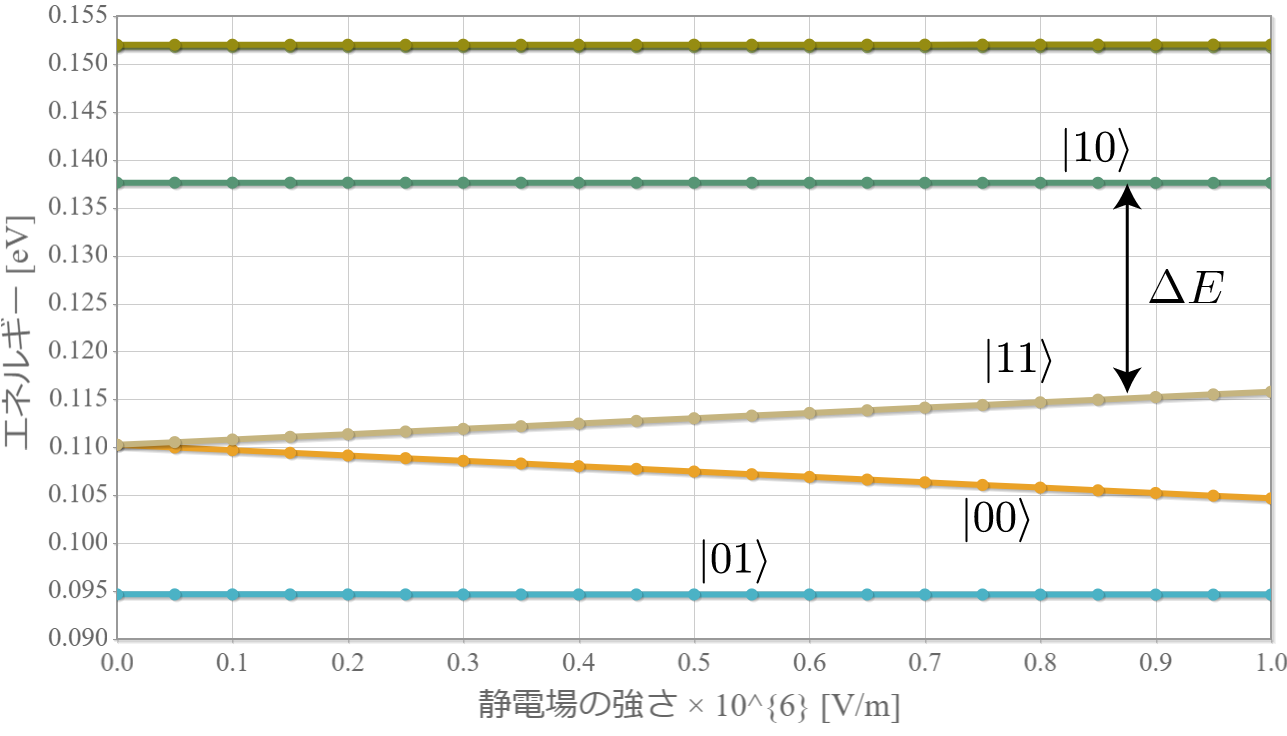
前回、電子同士のクーロン相互作用を考慮した独立した2つの2重量子井戸の電子の固有状態を計算したね。今回はさらに静電場を加えるね。壁の幅と高さは、$W = L/5= 2.0 \times 10^{-9} [{\rm m}] = 2.0[{\rm nm}]$、$V_0 = 3.0[{\rm eV}]$ として、量子井戸の間隔は $R = 20.0[{\rm nm}]$ とするよ。次の結果は、静電場の大きさを $E_x = 0.1\times10^{6}[{\rm V/m}]$ から $1.0\times10^{6}[{\rm V/m}]$ まで $ 0.05\times10^{6}[{\rm V/m}]$ づつ強くしたときの基底状態から第3励起状態までの電子存在確率の空間分布だよ。想定通りだけれども、ちょっとした静電場で第1励起状態と第2励起状態の縮退が解けて、2重量子井戸の壁の左右に分かれる形になったね。それぞれの量子井戸の左に電子がいる状態を $|0\rangle$、右にいる状態を$|1\rangle$ と表すと、それぞれの電子状態は固有エネルギーが低い順番に $|01\rangle, |00\rangle, |10\rangle, |11\rangle$ と表わすことができるね。
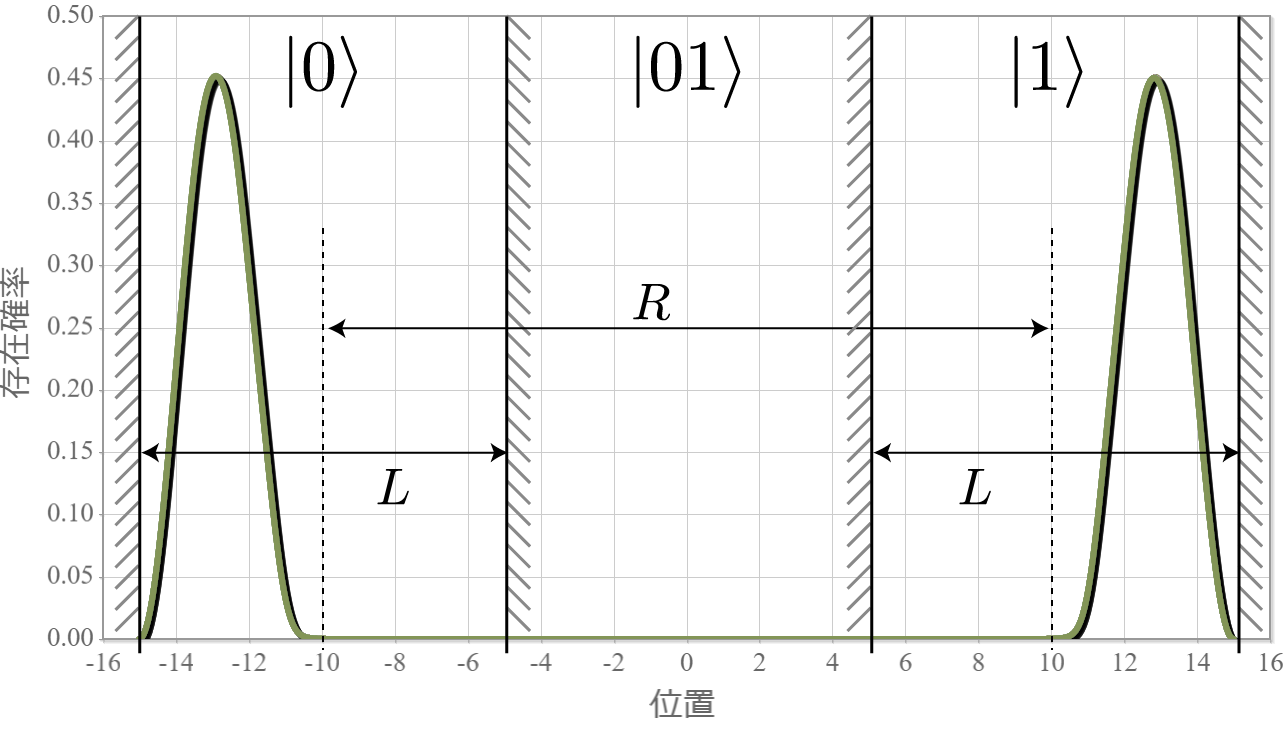
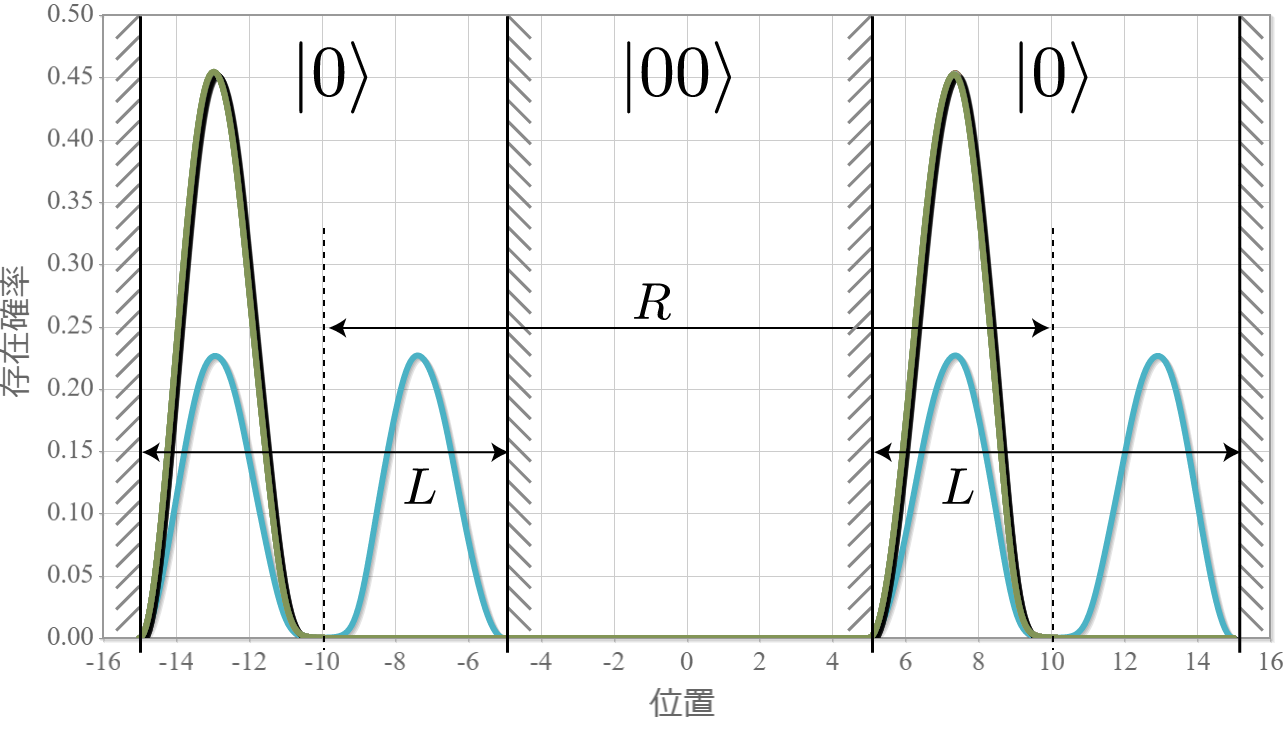
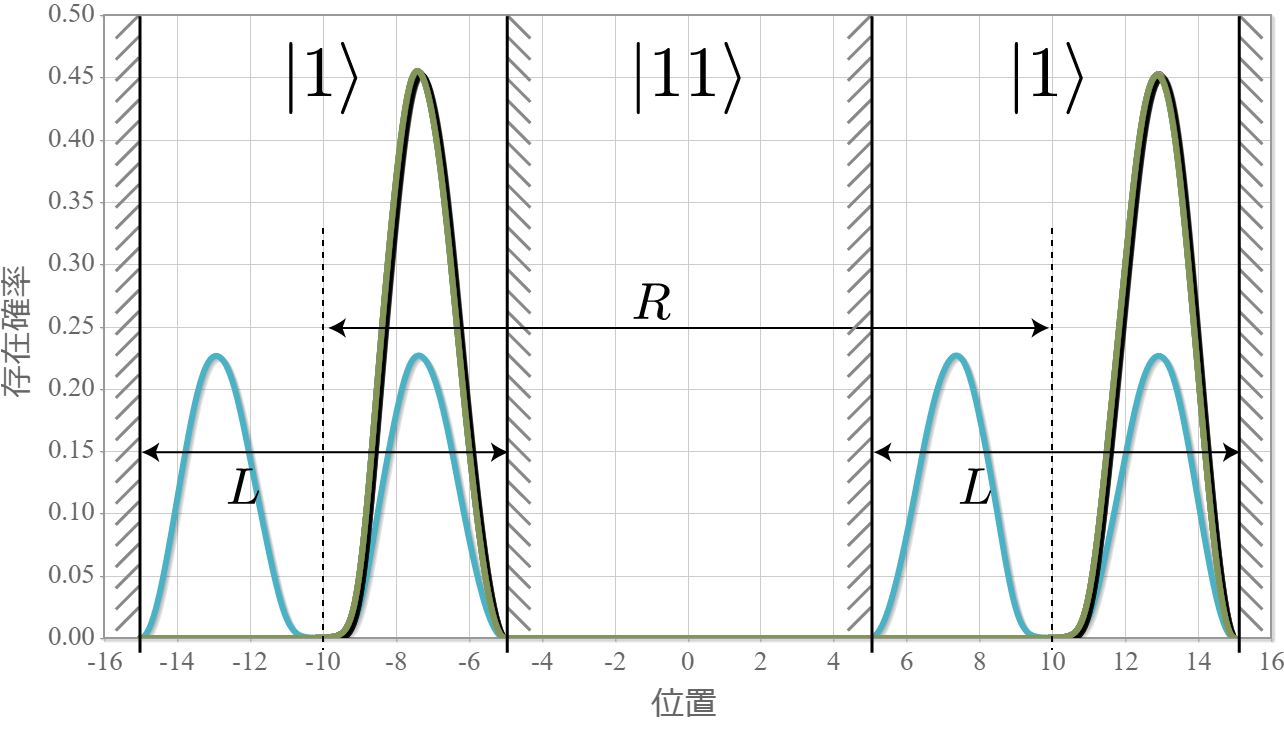
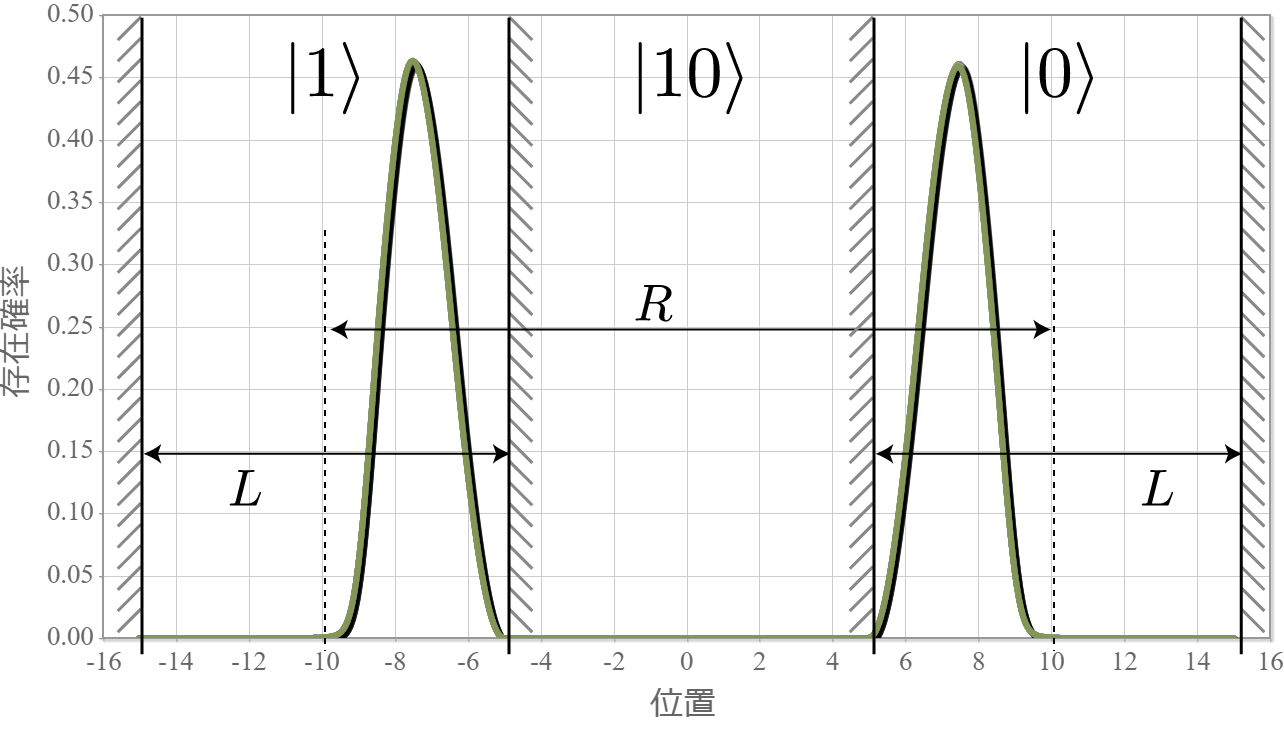
次の図は、上記の固有状態に対応するエネルギー準位の静電場の強度 $E_x$ 依存性だよ。想定通り、電場強度に比例して第1励起状態と第2励起状態の縮退が解けていく様子がわかるね。まさにシュタルク効果だね。今回は、エネルギー準位とは関係せずに電子が左か右かで $|0\rangle, |1\rangle$ を定義したけれども、エネルギー準位を基準として、2つの量子井戸の外側と内側で $|0\rangle, |1\rangle$ を定義すれば、固有エネルギーの低い順に $|00\rangle, |01\rangle, |10\rangle, |11\rangle$ と並ばせることもできるね。そして、下図の $\Delta E$ に対応する電磁波を外部から照射すれば、ラビ振動で $|10\rangle$ と $|11\rangle$ の状態遷移を起こすことができるので、制御・NOT演算が実現できるね。
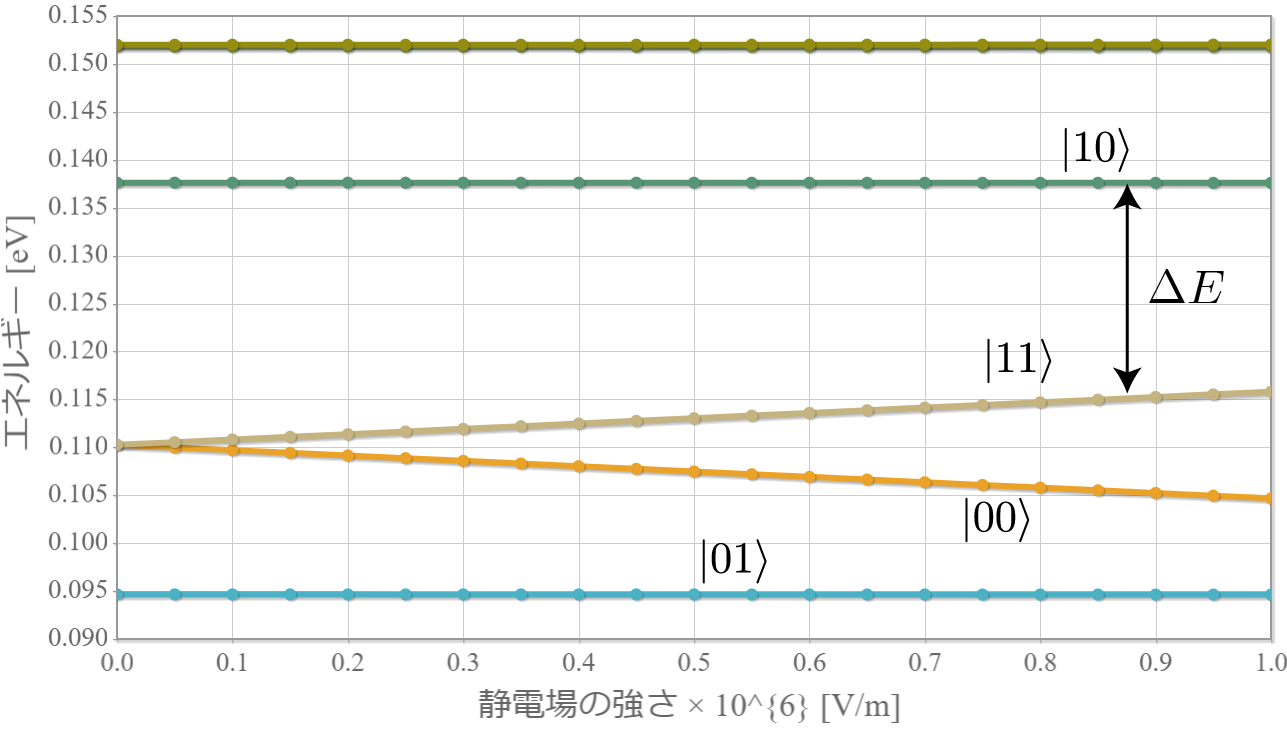
次回は実際にラビ振動をシミュレーションして、制御・NOT演算を確かめてみよう!
【量子コンピュータを作ろう!】(10)2重量子ドットに束縛された電子に静電場を加えたときの固有状態の計算結果(シュタルク効果)
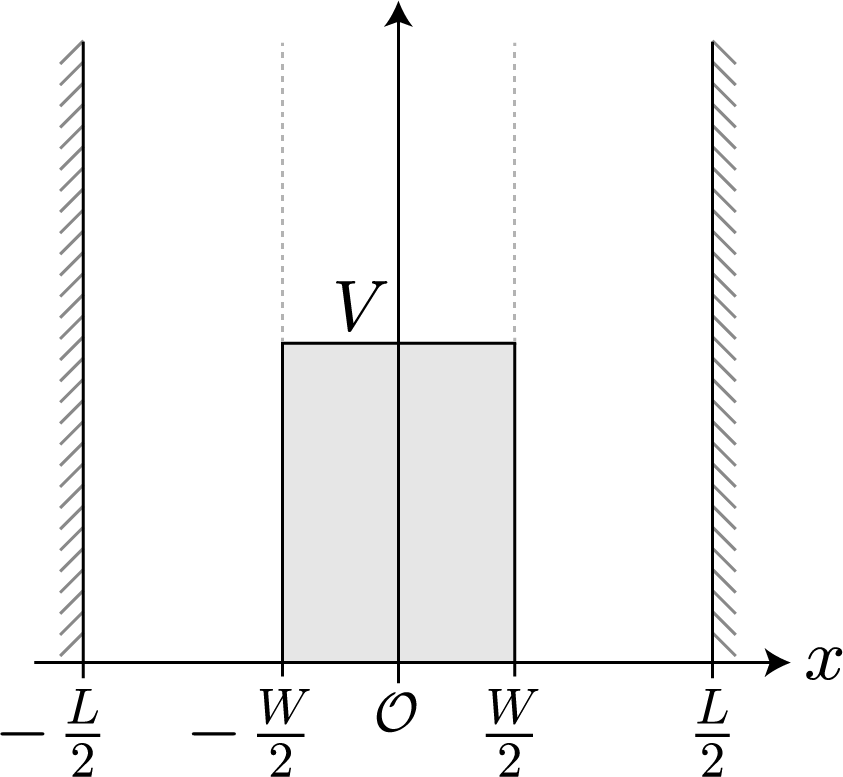
前回計算した2重量子ドットに束縛された電子の固有状態にさらに外部から静電場を加えたときの様子をシミュレーションするよ(静電場の向き:x軸の正方向)。電子分布が偏ってエネルギー準位がシフトするシュタルク効果が期待できるね。2重井戸の場合はどんな形になるのかな。ハミルトニアンのポテンシャル項は次のとおりだよ。
\begin{align}
V(x) = \left\{ \matrix{ \infty & x \leq -\frac{L}{2} \cr e E_x x & -\frac{L}{2} \leq x\leq -\frac{W}{2} \cr V & -\frac{W}{2}
\leq x\leq \frac{W}{2} \cr e E_x x& \frac{W}{2} \leq x\leq \frac{L}{2} \cr \infty & \frac{L}{2} \leq x} \right.
\end{align}
なお、具体的なパラメータとして、量子井戸全体のサイズを $L = 10[{\rm nm}]$、真ん中の壁のサイズを $W = 2[{\rm nm}]$、壁の高さを $0.3[{\rm eV}]$ として、静電場の強さを $0 \sim2.0\times10^{6}[{\rm V/m}]$ と $0.1$ ずつ変化させてみたよ。まずは、固有状態から見てみよう!
固有状態の空間分布
基底状態と第一励起状態
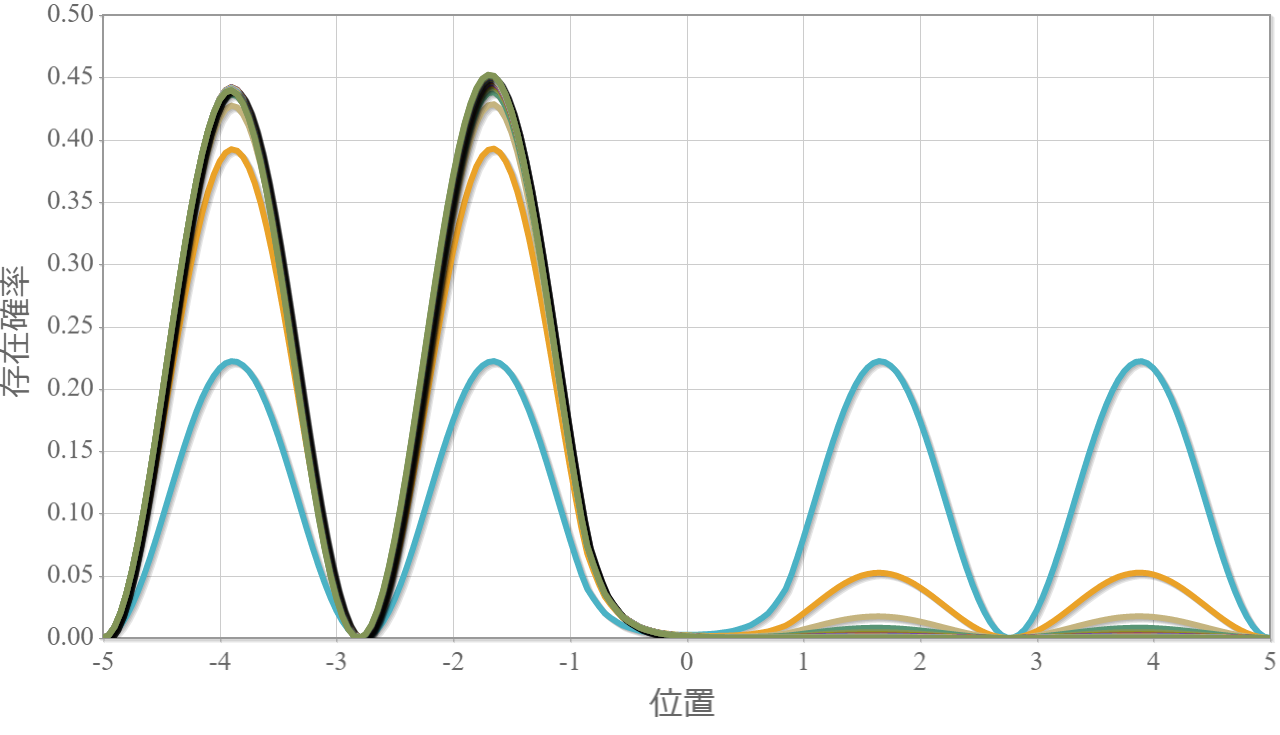
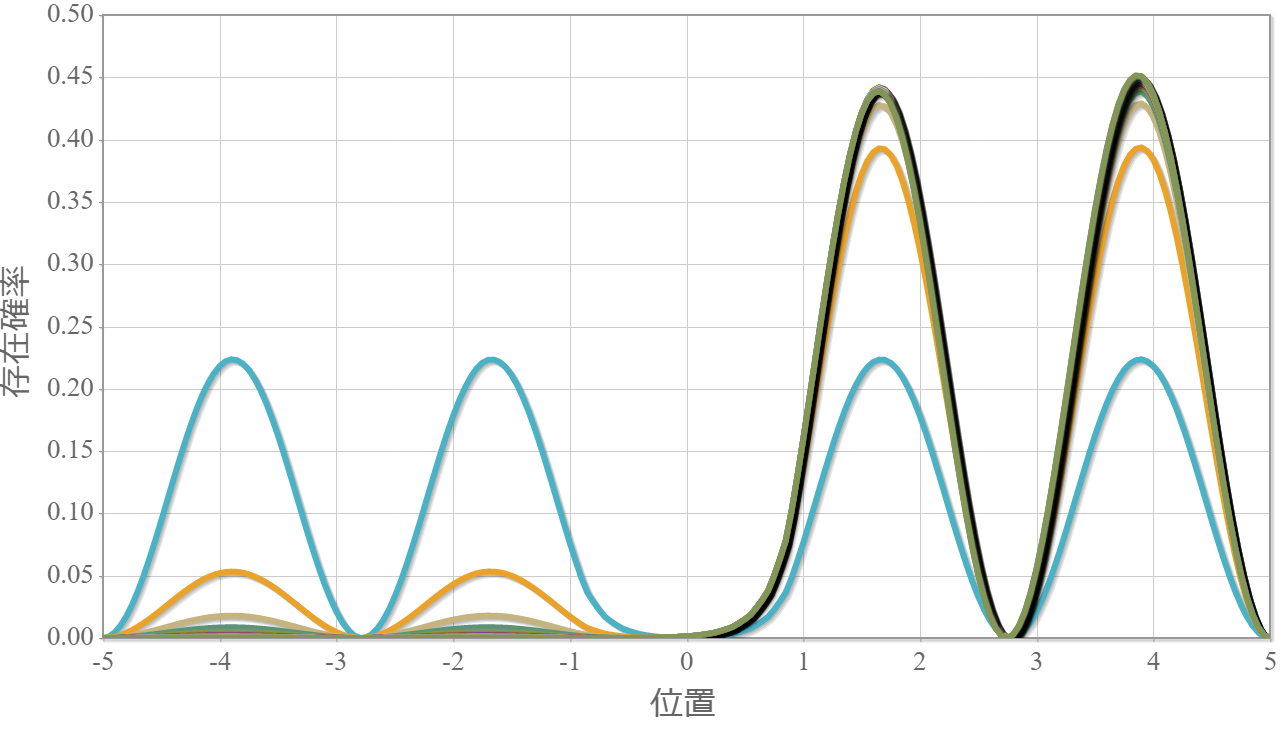
次の図は、静電場の強さを $0 \sim2.0\times10^{6}[{\rm V/m}]$ と $0.1$ ずつ変化させたときの基底状態(左)と第一励起状態(右)の空間分布だよ。静電場を少し加えただけで、電子は片端に偏っているね。ちょっとした外部静電場で電気双極子が生じていると言えるね。興味深いことに、真ん中に壁が無い場合の電気双極子と比較して、かなり弱い電場強度で同等の分極率(100倍)が得られているね(壁無し:$10\times10^{6}$ で基底状態のピーク位置が$2.7[{\rm nm}]$ 程度、壁有り:$0.1\times10^{6}$ でピーク位置が$2.7[{\rm nm}]$ 程度)。特に壁無しの第一励起状態は分極率は小さそうだったので、かなりの差だと言えるね。
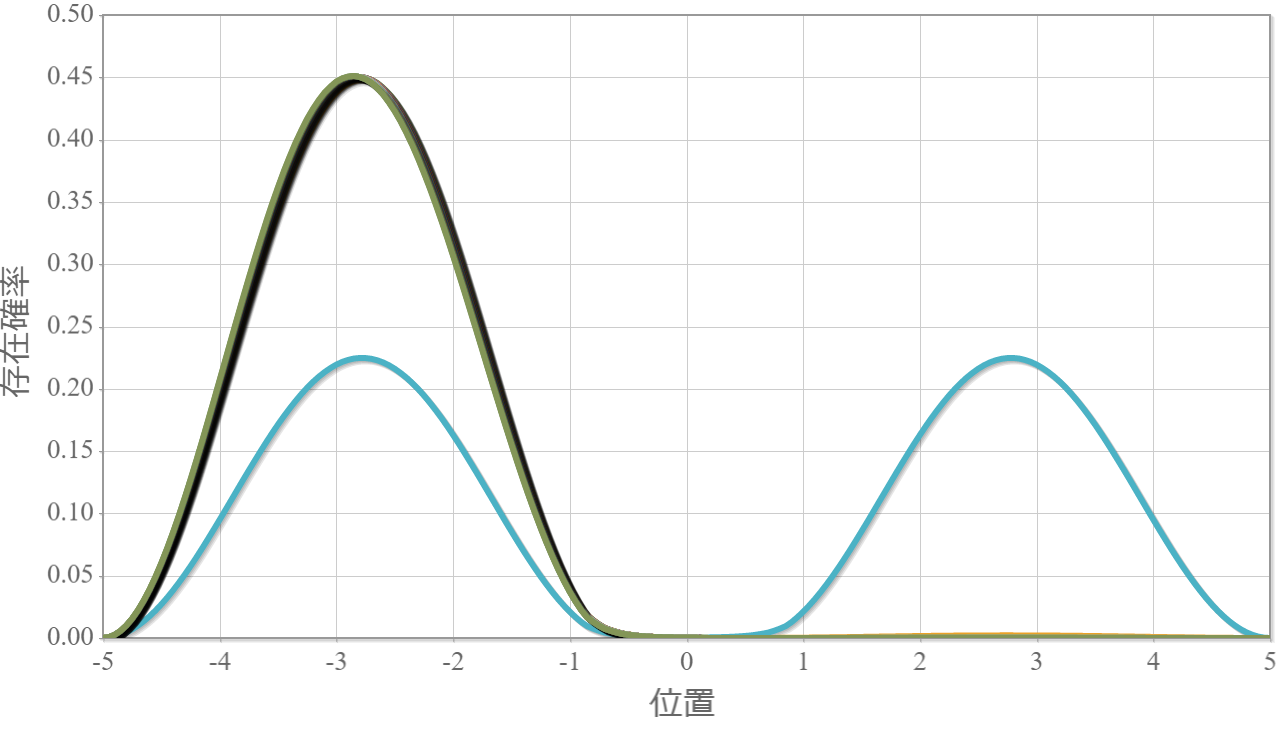
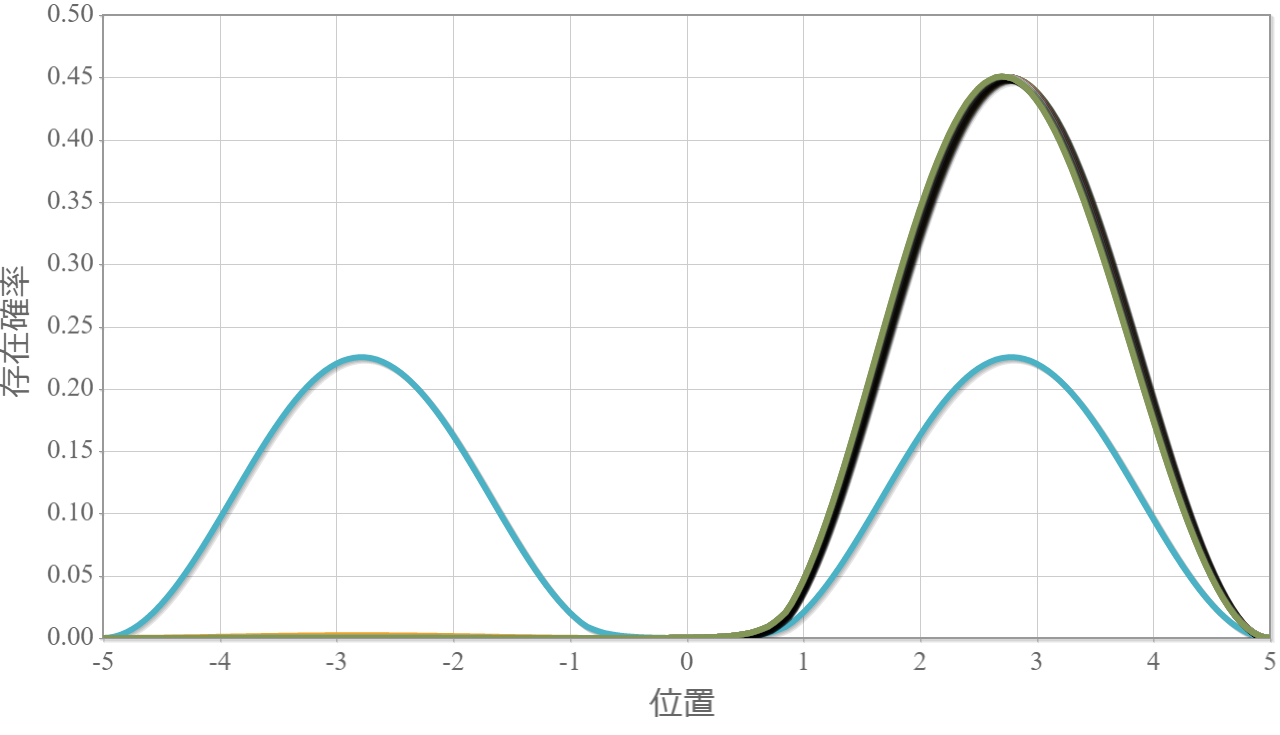
第二励起状態と第三励起状態
次の図は、静電場の強さを $0 \sim2.0\times10^{6}[{\rm V/m}]$ と $0.1$ ずつ変化させたときの第二励起状態(左)と第三励起状態(右)の空間分布だよ。静電場を $0.3 \times10^{6}[{\rm V/m}]$程度加えただけで、電子は片端に偏っているね。基底状態に対してより強い電場が必要なのは、もともとエネルギーが高い状態だからだね。
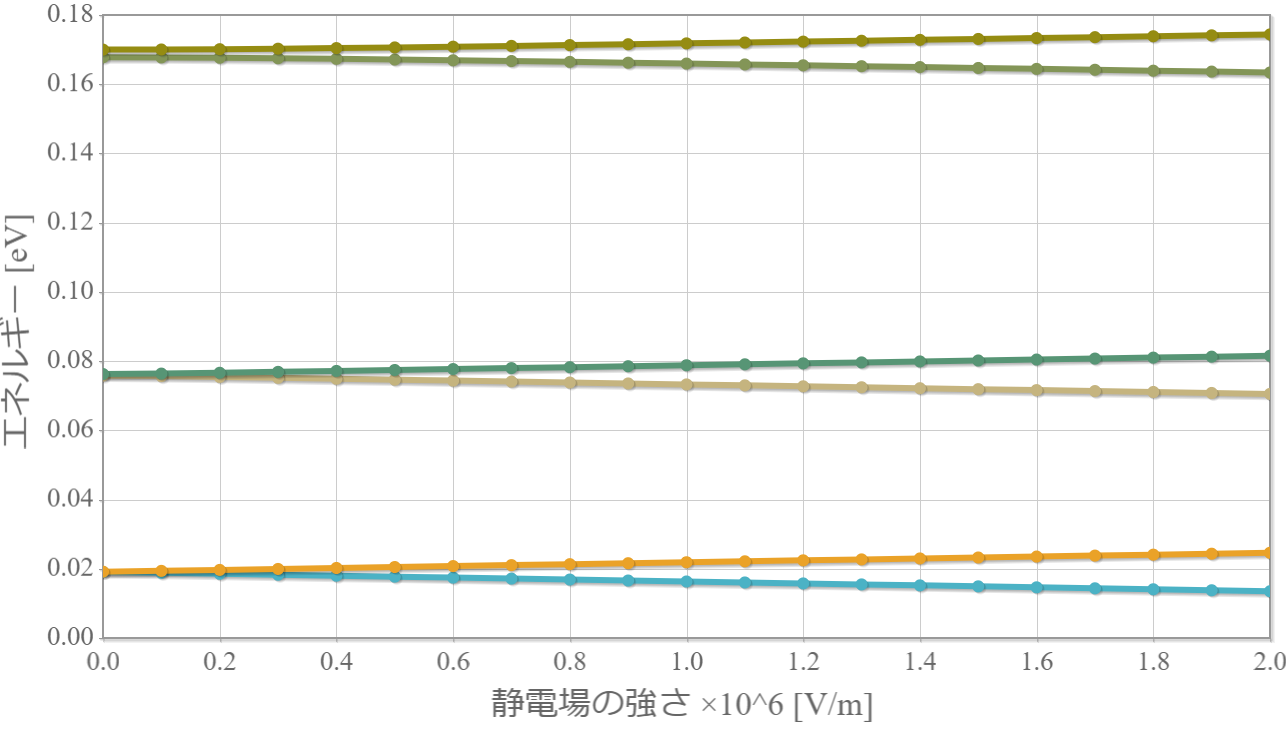
エネルギー準位の静電場依存性
次の図は下から6つのエネルギー準位の壁の高さ依存性だけれども、通常のシュタルク効果と同様、静電場によって縮退している状態が解けて、電場強度に比例した大きさのエネルギーシフトが見られるね。先に示したとおり、僅かな静電場で電気双極子が得られるので、この2重量子井戸をそのまま1量子ビットに用いることで、量子ビット間の相互作用を強めることができる可能性があるね。
次回はいよいよ電子2個に進むよ。まずは1重の量子井戸に2個の電子を束縛したときの固有状態を計算するよ。
【量子コンピュータを作ろう!】(6)量子ドットに束縛された電子に静電場+電磁波を加えたときの状態遷移の計算結果(シュタルク効果+ラビ振動)
まず、次の図は量子ドットに束縛された電子に $E_x = 2\times10^{6}[{rm eV}]$ の大きさの静電場を加えてることで変化した基底状態と励起状態だよ。基底状態は電場の向きの反対側に分布が偏って、励起状態は反対に電場の向きと同じ方向に分布が偏っているね。これは電気双極子が生じていると考えられるね。基底状態と励起状態の電気双極子はそれぞれ $\boldsymbol{p}_0 = -2e \langle \tilde0|x |\tilde0\rangle >0$ と $\boldsymbol{p}_1 = -2e \langle \tilde1|x |\tilde1\rangle< 0 $ となるよ。これらの電気双極子と静電場との相互作用によって、静電エネルギーは $ \Delta U = \boldsymbol{p} \cdot \boldsymbol{E} $ だけ変化するよ。さらに、この電気双極子によって生じる電場によって、外部から基底状態と励起状態のどちらの準位に存在するか測定することができるね。
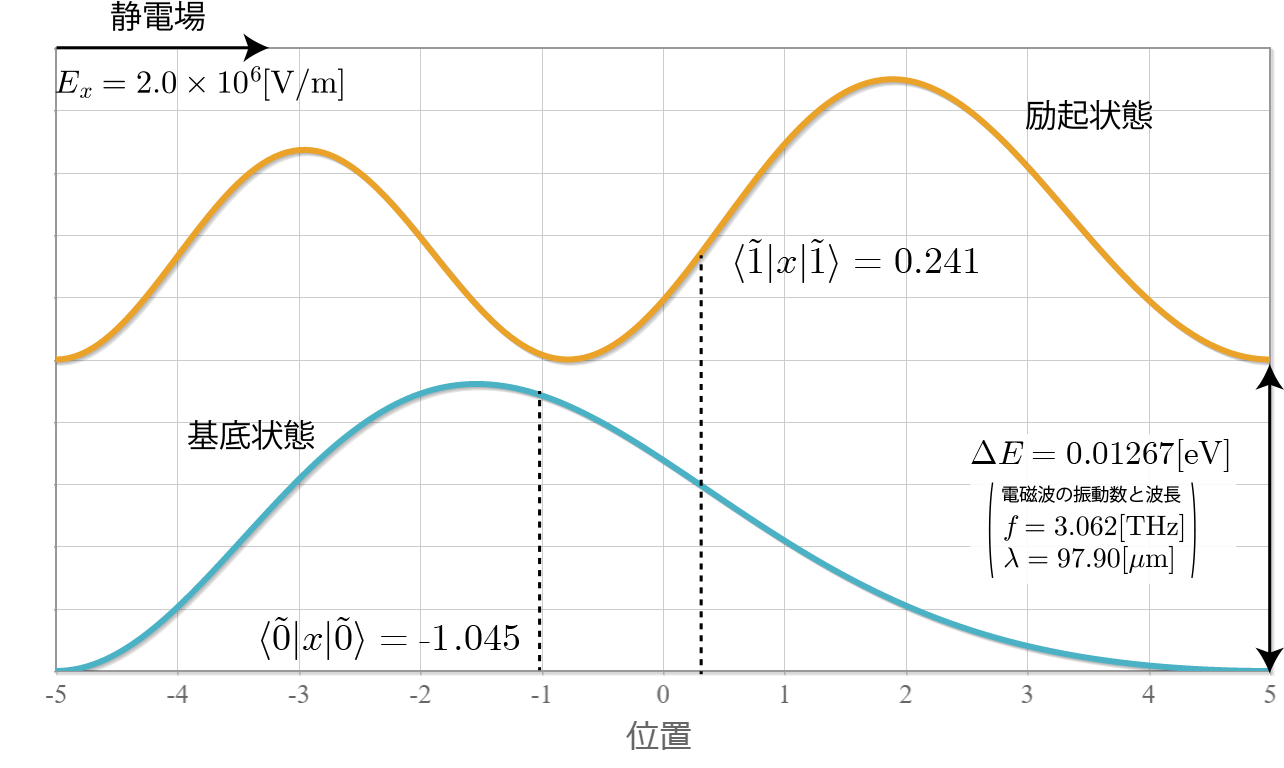
次に、この2準位間のエネルギー差($\Delta E = 0.01267 [{\rm eV}]$)に対応する光子エネルギーの電磁波(振動数:$f = 3.062 [{\rm THz}] $、波長:$\lambda = 97.90 [{\rm \mu m}] $)を入射して、2準位間のラビ振動をシミュレーションした結果を示すよ。想定通り、2準位間をsin関数的に遷移する様子が確認できたね。
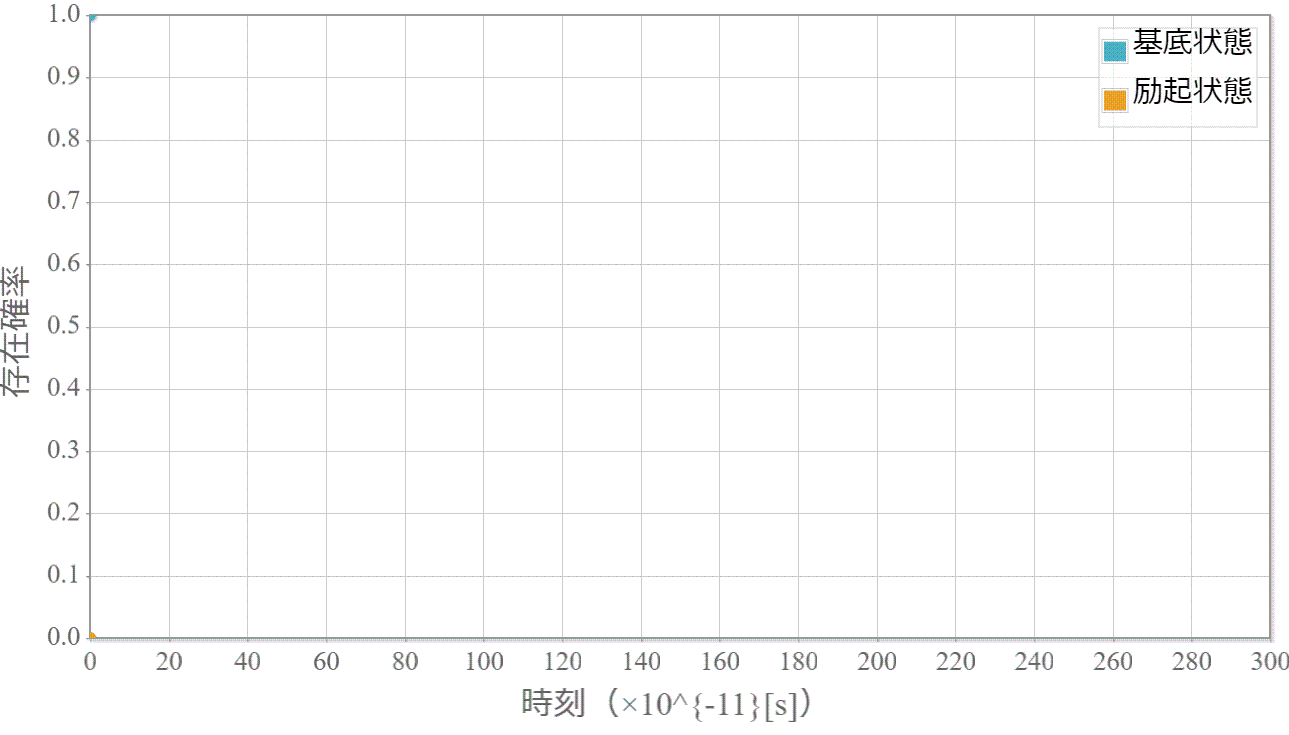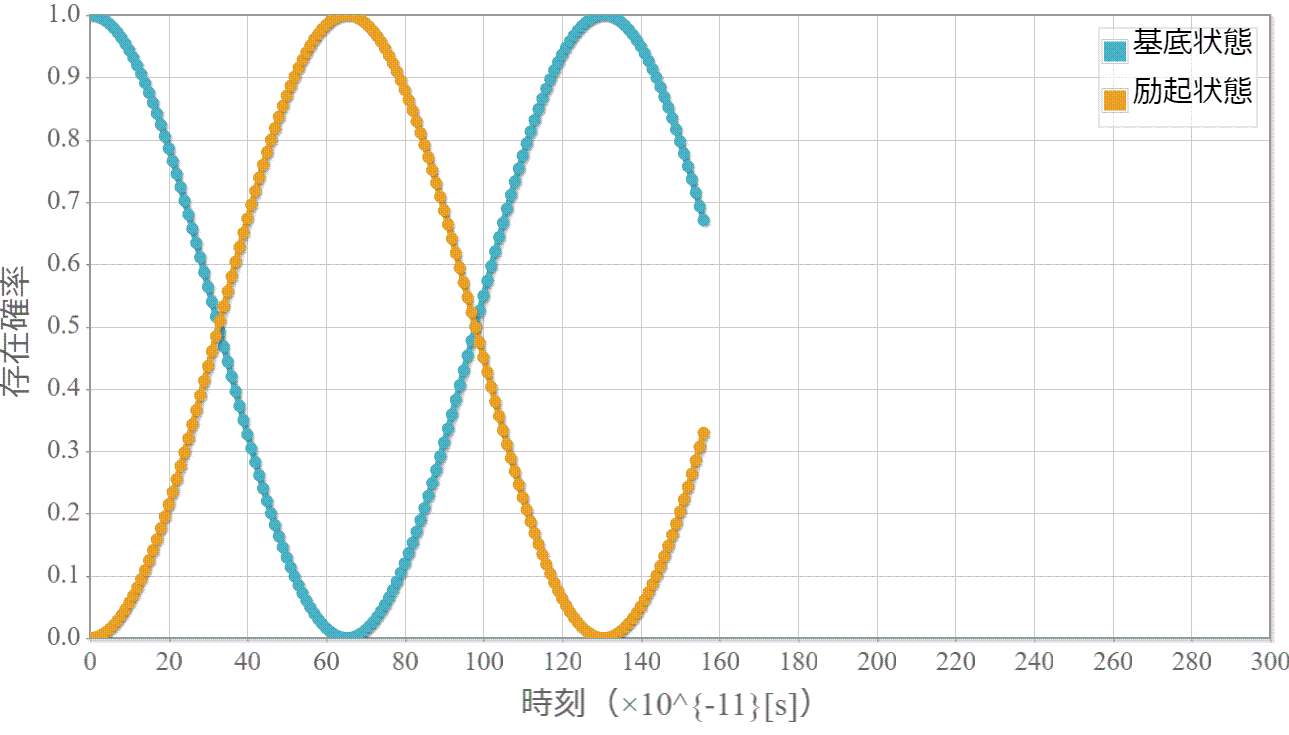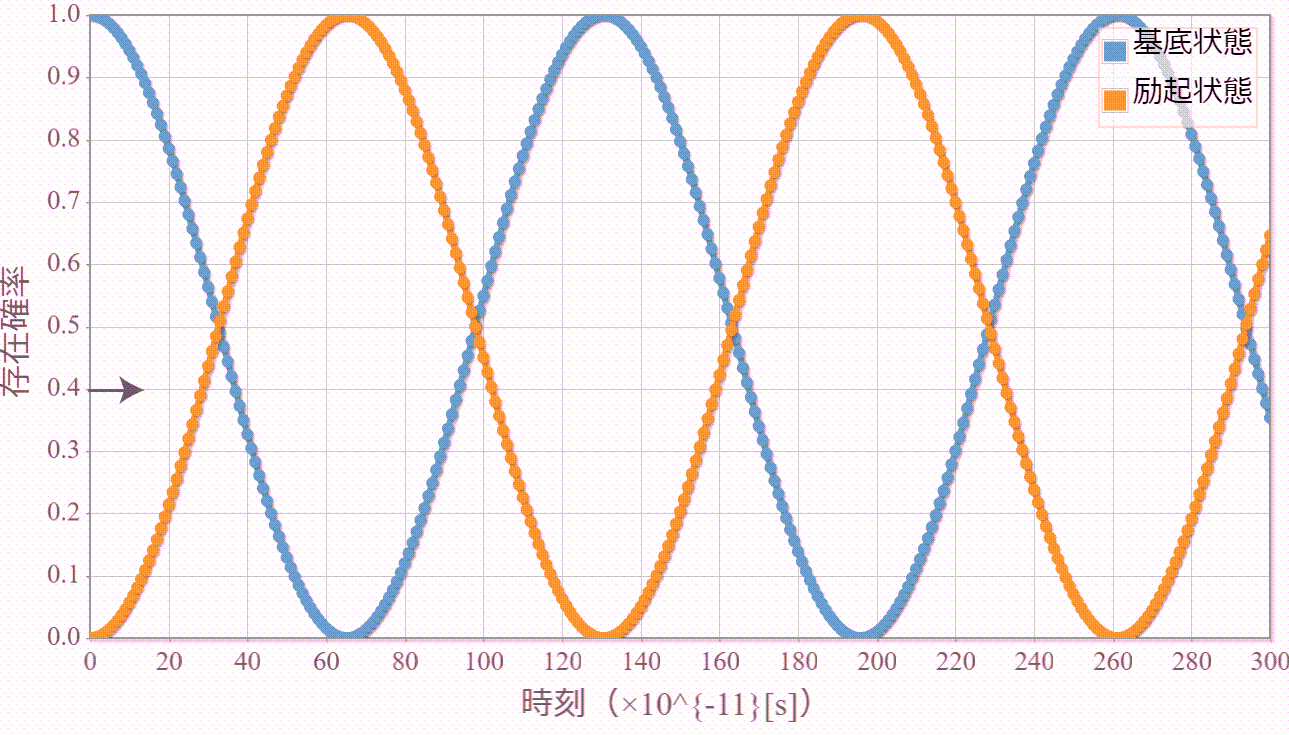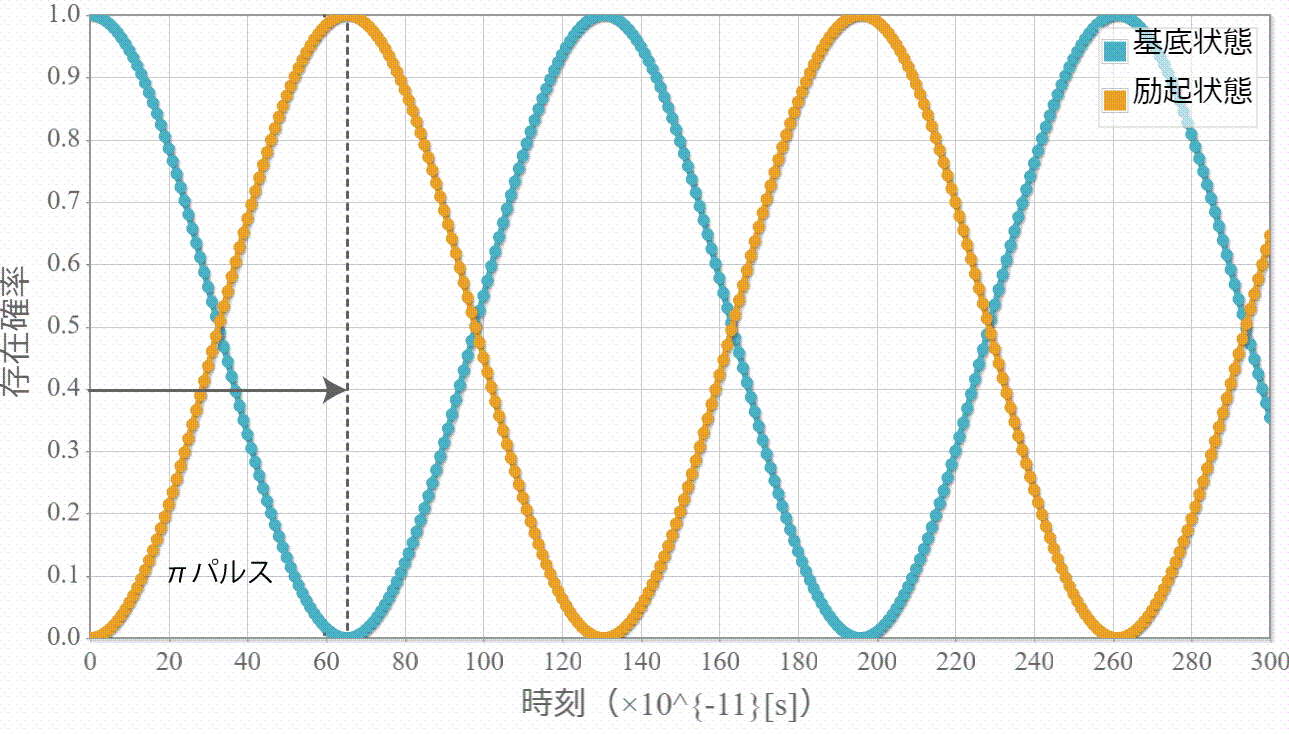
【量子コンピュータを作ろう!】(5)量子ドットに束縛された電子に静電場+電磁波を加えたときのハミルトニアンと計算方法(シュタルク効果+ラビ振動)
量子ドットに束縛された電子に静電場を加えてることで変化した基底状態と第一励起状態に対して、外部から電磁波を与えて状態遷移の時間発展させることを考えるよ。静電場を加え無い場合と同様にラビ振動するはずだけれども、ちゃんとシミュレーションできるかどうかを確かめるよ。この場合のハミルトニアンは次のとおりだね。
\begin{align}
\hat{H} = -\frac{\hbar^2}{2m_e} \frac{d^2}{dx^2} + e E_x x + \frac{e}{m_e} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}
\end{align}
静磁場を加えたときの固有状態は数値的はすでに解けているので、そのハミルトニアンを $\hat{H}_{\rm Field}$ と表して、その固有関数を $\tilde{\varphi}_n(x)$、固有エネルギーを $\tilde{E}_n$ と表すと、次の固有方程式
\begin{align}
\hat{H}_{\rm Field} \tilde{\varphi}_n(x) = \tilde{E}_n\tilde{\varphi}_n(x)
\end{align}
を満たすね。ちなみに固有状態を明示的に表しておくと
\begin{align}
\tilde{\varphi}_n(x) = \sum\limits_{n’=0} a^{(n)}_{n’}\varphi_{n’}(x) = \sqrt{\frac{2}{L}} \sum\limits_{n’=0} a^{(n)}_{n’} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ k_n = \frac{\pi(n+1)}{L}
\end{align}
となって、この $a^{(n)}_{n’}$ が既知であるという意味だよ。このハミルトニアン $\hat{H}_{\rm Field}$ を用いて、元のハミルトニアンは
\begin{align}
\hat{H} = \hat{H}_{\rm Field} + \frac{e}{m_e} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}
\end{align}
と表すことができて、$\tilde{E}_n$ と $\tilde{\varphi}_n(x)$ はすでに既知なので、前回と同様にラビ振動をシミュレーションできそうだね。今回も1次元系で考えているので、ベクトルポテンシャルを $\boldsymbol{A}(t) = (A_x(t), 0, 0)$ として、
\begin{align}
A_x(t) = A_0 \cos(kx-\omega t)
\end{align}
と考えるよ。そして、電磁波を入射するときの波動関数を
\begin{align}
\tilde{\psi}(x, t) = \sum\limits_{n=0} \tilde{a}_n(t) \tilde{\varphi}_n(x)
\end{align}
という感じに、展開してその係数の値が時間に依存すると考えるよ。これを時間依存を考慮したシュレーディンガー方程式
\begin{align}
i \hbar \frac{\partial }{\partial t} \tilde{\psi}(x, t) = \hat{H} \tilde{\psi}(x, t)
\end{align}
に代入して、両辺に $\tilde{\varphi}^*_m(x)$ を掛けて全空間で積分するよ。すると、$\tilde{a}_m(t)$ に関する連立常微分方程式が得られるね。
\begin{align}
i \hbar \frac{d \tilde{a}_m(t)}{d t} = E^{(0)}_m \tilde{a}_m(t) + \sum\limits_{n=0} \langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle \tilde{a}_n(t)
\end{align}
$\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle$ は、
\begin{align}
\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \tilde{\varphi}^*_m(x) \hat{V}(t)
\tilde{\varphi}_n(x)\, dx = \sum\limits_{n’, m’=0} a^{(m)*}_{m’} a^{(n)}_{n’} \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_{m’}(x) \hat{V}(t)
\varphi_{n’}(x)\, dx = \sum\limits_{n’, m’=0} a^{(m)*}_{m’} a^{(n)}_{n’} \langle m’ | \hat{V}(t) | n’ \rangle
\end{align}
となって、静電場が無い場合の固有関数の積分の和で表すことができるね。$\hat{p}_x/m_e = [\hat{H}_0, x ]/i\hbar$ を考慮すると
\begin{align}
\langle m’ | \hat{V}(t) | n’ \rangle = \frac{1}{L}\int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_{m’}(x) \hat{V}(t)
\varphi_{n’}(x)\, dx = \frac{eA_0}{m_e} \langle m’ | \cos(kx-\omega t) p_x | n’ \rangle = \frac{eA_0}{i\hbar} \langle m’ | \cos(kx-\omega t) [\hat{H}_0, x ] | n’ \rangle
\end{align}
と変形できて、今回も波長が量子ドットのサイズよりも十分大きいと仮定すると、$kx \simeq 0$ と近似することができるので
\begin{align}
\langle m’ | \hat{V}(t) | n’ \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) \left[ E^{(0)}_{m’} – E^{(0)}_{n’} \right] \langle m’ |
x | n’ \rangle
\end{align}
となるので、最終的に $\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle$ は
\begin{align}
\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) \sum\limits_{n’, m’=0} a^{(m)*}_{m’} a^{(n)}_{n’} \left[ E^{(0)}_{m’} – E^{(0)}_{n’} \right] \langle m’ | x | n’ \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) K_{mn}
\end{align}
となるね。$K_{mn}$ は一度計算するれば良いので、これを用いて、展開係数$\tilde{a}_m(t)$ に関する連立常微分方程式は
\begin{align}
i \hbar \frac{d \tilde{a}_m(t)}{d t} = \tilde{E}_m \tilde{a}_m(t) + \frac{eA_0}{i\hbar} \cos(\omega t)\sum\limits_{n=0} K_{mn} a_n(t)
\end{align}
となるね。この $\tilde{E}_m, K_{mn}$ はあらかじめ計算することができるね。電磁波の角振動数が2準位間のエネルギー差 $\Delta E = \tilde{E}_1 – \tilde{E}_0$ と表して $\omega = \Delta E / \hbar$ となるときに、2準位間を周期的に遷移するね。次回はこれをシミュレーションするよ。
【量子コンピュータを作ろう!】(2)量子ドットに束縛された電子に静電場を加えたときの固有状態の計算結果(シュタルク効果)
前回、定式化した量子ドットに束縛された電子に静電場を加えたときの固有状態の計算結果を示すよ。量子井戸の横幅は $L = 10 \times 10^9 [{\rm m}]$( $=10[{\rm nn}]$ )としているよ。
基底状態と第一励起状態の固有エネルギーの静電場の強度依存性
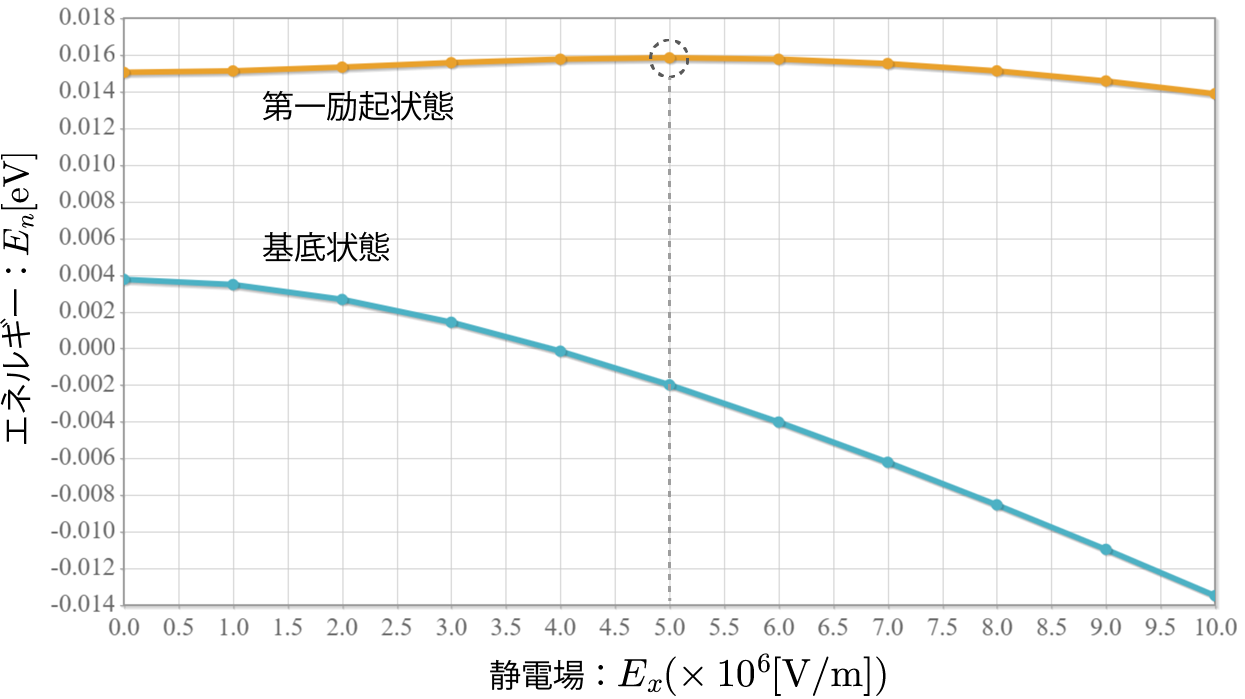
次のグラフは基底状態と第一励起状態の固有エネルギーの静電場の強度依存性だよ。基底状態は電場強度が強くなるにつれてエネルギーが下がっているのに対して、第一励起状態は電場強度が強くなるにつれて初めエネルギーが上がっていった後に下がって行く様子がわかるね。その分岐点となる電場強度はおおよそ $E_x = 5.0\times 10^6 [{\rm V/m}]$ であることがわかるね。静電場が加わることでエネルギーが上下する理由は電気双極子が誘起されていることを意味しているよ。エネルギーが下がるのは電気双極子モーメントが静電場の向きと平行となり、反対に上がるのは電気双極子モーメントが静電場の向きと反平行となっていると考えられるね。
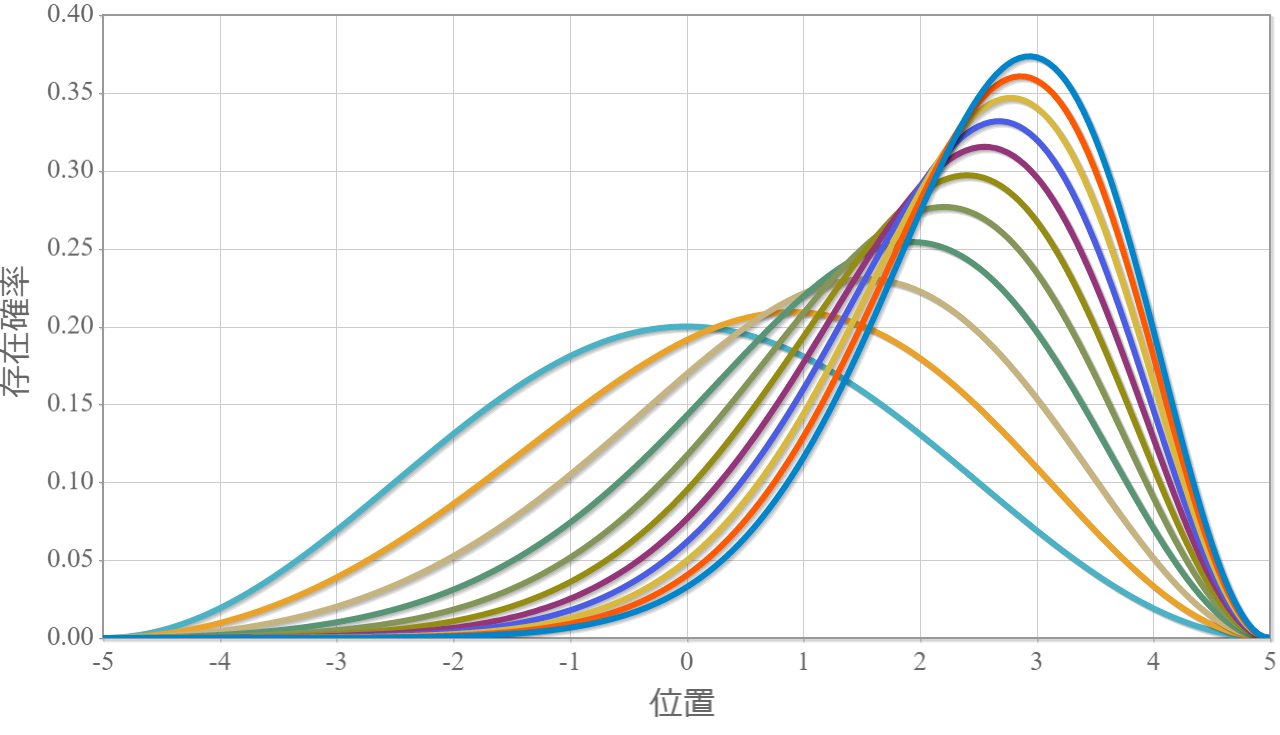
基底状態と第一励起状態の固有関数の静電場強度別の空間依存性
次のグラフは基底状態の固有関数の静電場強度別の空間依存性だよ($E_x = 0.0\times 10^6 \sim 1.0\times 10^6 [{\rm V/m}]$)。静電場が強くなるほど電子の分布がx軸の正方向に偏っていくね。つまり、電気双極子モーメントが大きくなっていることに対応しているよ。
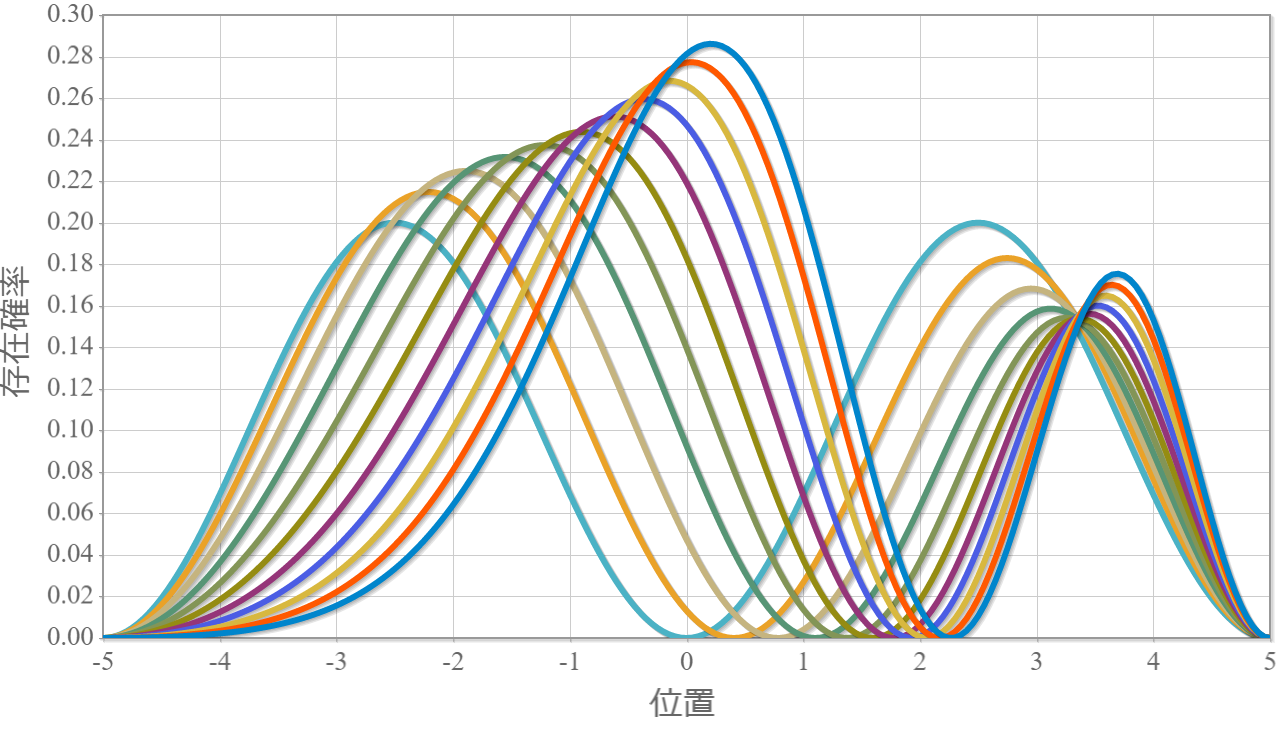
次のグラフは第一励起状態の固有関数の静電場強度別の空間依存性だよ($E_x = 0.0\times 10^6 \sim 10.0\times 10^6 [{\rm V/m}]$)。第一励起状態はエネルギー準位の電場強度依存性からも分かる通り、$E_x = 5.0\times 10^6 [{\rm V/m}]$ までは、電場強度に応じて電子分布はx軸の負方向に偏っていくね。それよりも大きな電場を加えると、反対にx軸の正方向に偏っていくね。
以上の結果より、外部から静電場を加えることで、基底状態と第一励起状態は異なる向きの電気双極子モーメントが誘起されることがわかったね(シュタルク効果)。これを利用することで、基底状態と第一励起状態の区別をつけることができるよ。次回は、この基底状態と第一励起状態を入れ替えるラビ振動を確かめるよ。
【量子コンピュータを作ろう!】(1)量子ドットに束縛された電子に静電場を加えたときのハミルトニアンと計算方法(シュタルク効果)
量子コンピュータを勉強のために、シミュレーションが一番簡単そうな量子ドットに束縛された電子のエネルギー準位を量子ビットとして扱うタイプを念頭に置いて、量子コンピュータを実現するために必要な素子の具体的な物理系のシミュレーション(数値実験)を行っていくよ。今回は、1次元版量子ドット(井戸型ポテンシャル)に束縛された電子の状態を変化させるために静電場を加えたときの固有状態を調べるよ。
静電場を加えたハミルトニアンとシュレディンガー方程式
井戸型ポテンシャルに束縛された電子に外部からx軸方向の静電場 $E_x$ を加えると、電子は静電場によって空間分布が変化することが考えられるね。量子井戸の底のポテンシャルエネルギーを0としたときのハミルトニアンは次のとおりだね。
\begin{align}
\hat{H} = \hat{H}_0 + \hat{V} = -\frac{\hbar^2}{2m_e} \frac{d^2}{dx^2} – e E_x x \\
\end{align}
$\hat{V}$ は静電場によるポテンシャルエネルギーだよ。$\hat{H}_0$ は 外場無し($E_x = 0$)のときのハミルトニアンで、井戸の深さが無限大のときには固有関数 $\varphi_n(x)$ を用いて、エネルギー固有状態 $\hat{H}_0 \varphi_n(x) = E_n \varphi_n(x)$ を満たすよ。固有関数と固有エネルギーは
\begin{align}
\varphi_n(x) = \sqrt{\frac{2}{L}} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ E_n = \frac{\hbar^2 k_n^2}{2m_e} \ , \ k_n = \frac{\pi(n+1)}{L}
\end{align}
だね。$k_n$ は波数だよ。静磁場が加わったときの固有関数と固有エネルギーをそれぞれ $\varphi(x)$ と $E$ と表したとき、シュレディンガー方程式は
\begin{align}
\hat{H} \varphi(x)= E \varphi(x) \\
\end{align}
となるけれど、この $\varphi(x)$ を $\varphi_n(x)$ を用いて
\begin{align}
\varphi(x) = \sum\limits_{n=0} a_n \varphi_n(x)
\end{align}
と展開して、固有関数と固有エネルギーを計算するよ。
固有関数と固有エネルギーの計算方法
シュレディンガー方程式の両辺に $\varphi^*_m(x)$ を掛けて全空間で積分するよ。固有関数の直交関係を考慮すると、シュレディンガー方程式は
\begin{align}
E^{(0)}_m a_m + \sum\limits_{n=0} \langle m | \hat{V} | n \rangle a_n = E a_m
\end{align}
という展開係数 $ a_n $ に関する連立方程式になるね。ただし、$\langle m | \hat{V} | n \rangle $ は
\begin{align}
\langle m | \hat{V} | n \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_m(x) \hat{V} \varphi_n(x)\, dx
\end{align}
だよ。連立方程式は行列で表すとわかりやすくなるので、エネルギーの小さい順に固有関数の係数を並べると次のようになるよ。
\begin{align}
\left(\matrix{ E^{(0)}_0 +\langle 0 | \hat{V} | 0 \rangle & \langle 1 | \hat{V} | 0 \rangle & \langle 2 | \hat{V} | 0 \rangle & \langle 3 | \hat{V} | 0 \rangle & \langle 4 | \hat{V} | 0 \rangle & \cdots \cr
\langle 0 | \hat{V} | 1 \rangle & E^{(0)}_1 + \langle 1 | \hat{V} | 1 \rangle & \langle 1 | \hat{V} | 2 \rangle & \langle 1 | \hat{V} | 3 \rangle &\langle 1 | \hat{V} | 4 \rangle &\cdots \cr
\langle 0 | \hat{V} | 2 \rangle & \langle 1 | \hat{V} | 2 \rangle & E^{(0)}_2 + \langle 2 | \hat{V} | 2 \rangle & \langle 3 | \hat{V} | 2 \rangle& \langle 4 | \hat{V} | 2 \rangle& \cdots \cr
\langle 0 | \hat{V} | 3 \rangle & \langle 1 | \hat{V} | 3 \rangle & \langle 2 | \hat{V} | 3 \rangle & E^{(0)}_3 + \langle 3 | \hat{V} | 3 \rangle& \langle 4 | \hat{V} | 3 \rangle& \cdots \cr
\langle 0 | \hat{V} | 4 \rangle & \langle 1 | \hat{V} | 4 \rangle & \langle 2 | \hat{V} | 4 \rangle & \langle 3 | \hat{V} | 4 \rangle& E^{(0)}_4 + \langle 4 | \hat{V} | 4 \rangle& \cdots \cr
\vdots & \vdots & \vdots & \vdots & \vdots & \ddots } \right) \left(\matrix{ a_{0} \cr a_{1}\cr a_{2} \cr a_{3} \cr a_{4} \cr \vdots }\right) = E \left(\matrix{ a_{0} \cr a_{1}\cr a_{2} \cr a_{3} \cr a_{4} \cr \vdots }\right)
\end{align}
まさに行列表した固有値方程式の形になっているのがわかるね。 これで固有値と固有ベクトルを計算すると、固有値はそのまま外場が加えられた場合のエネルギー、固有ベクトルがそのまま展開係数の値そのものになるね。次回は、この計算結果を示すよ。
