タグ: 量子ドット

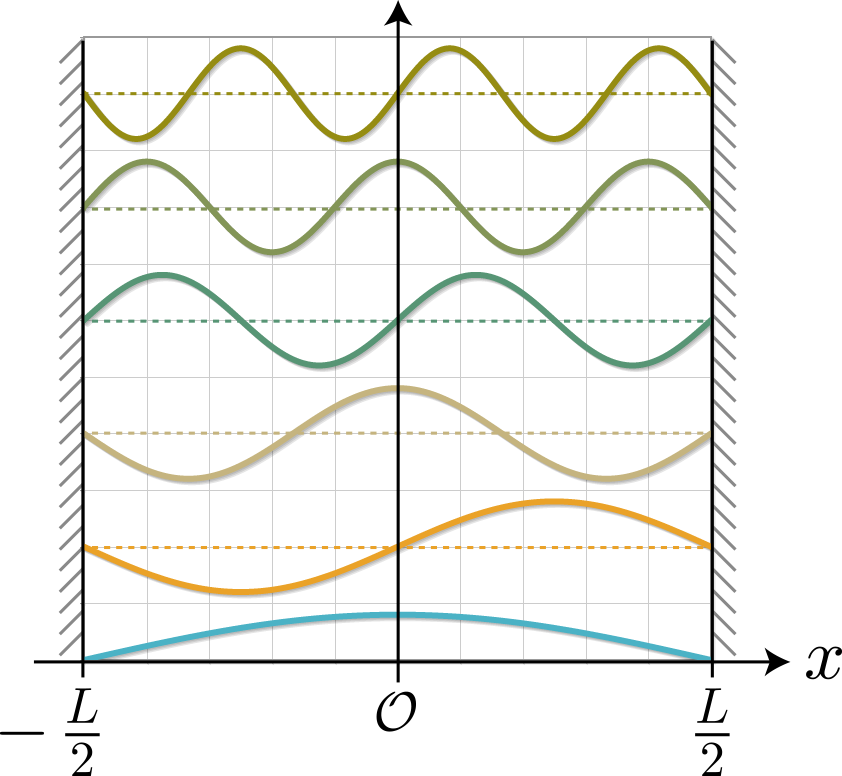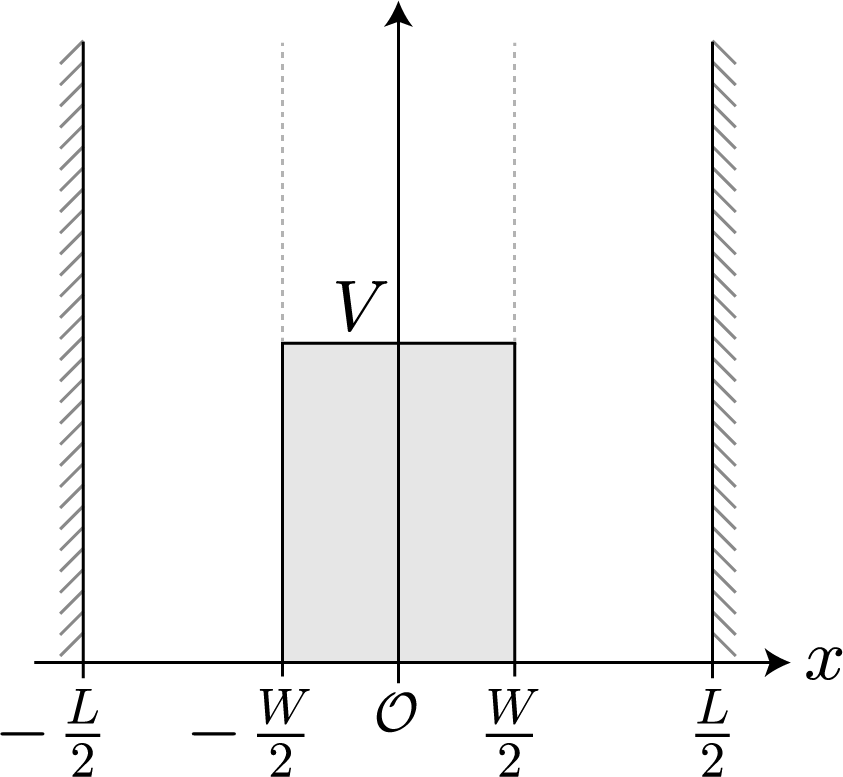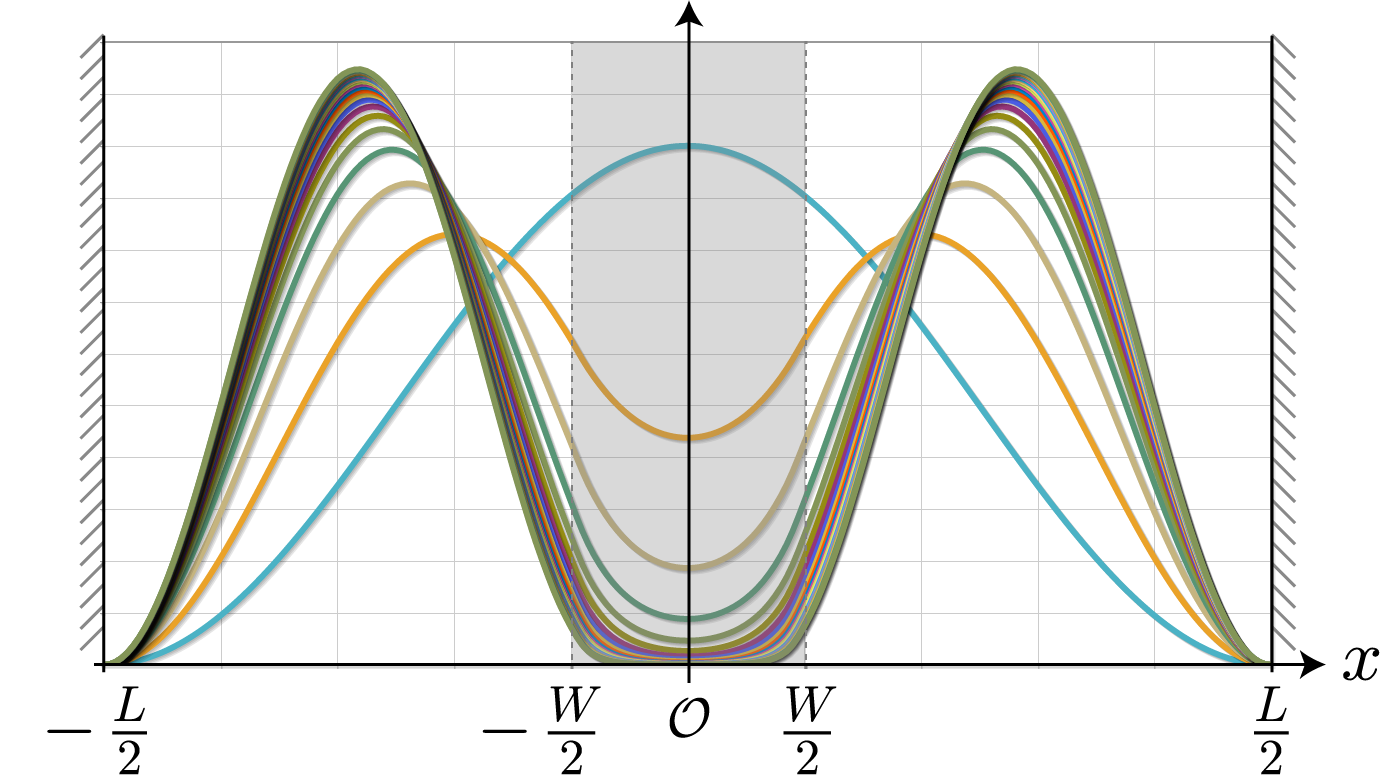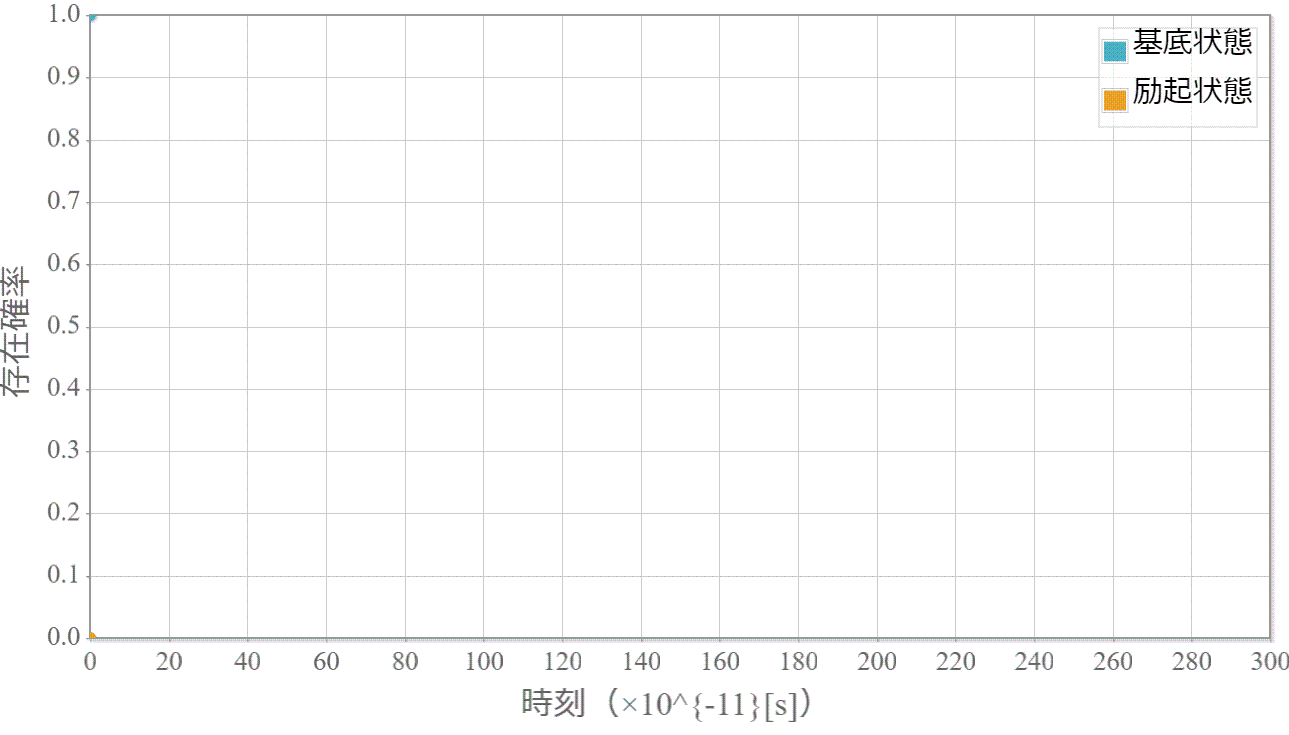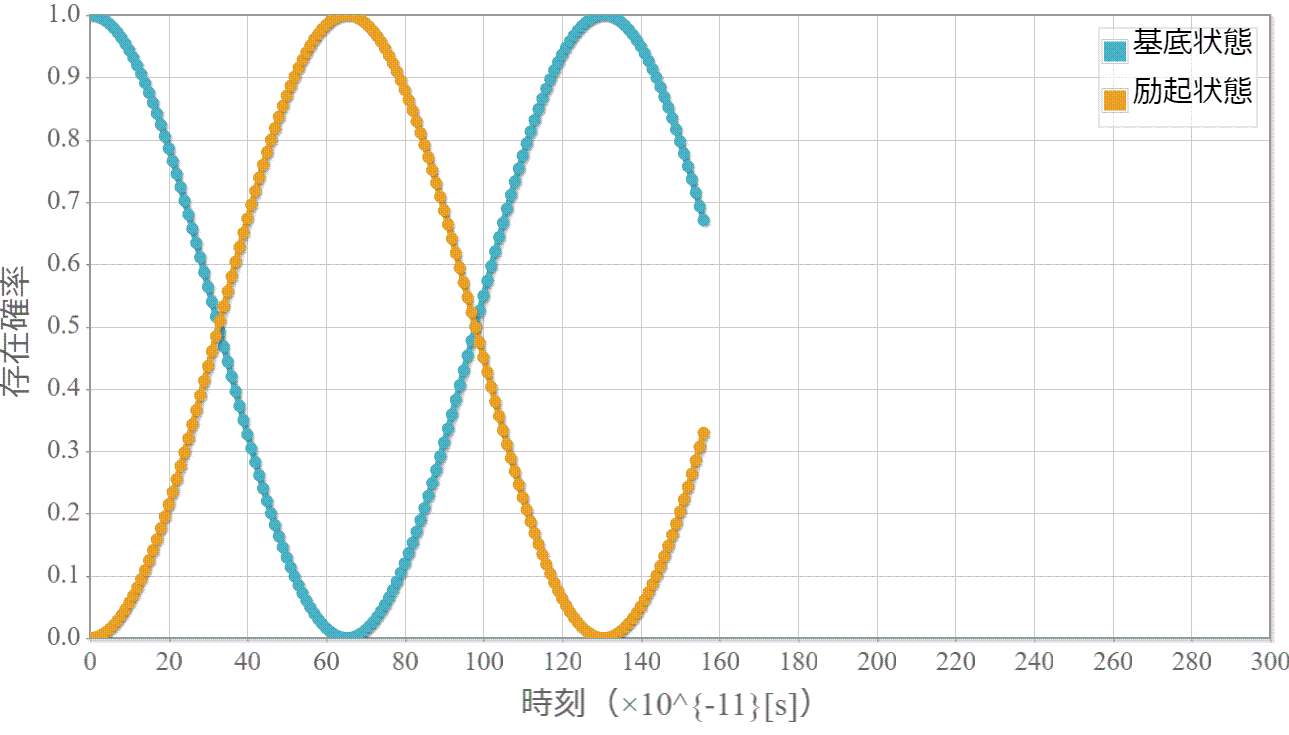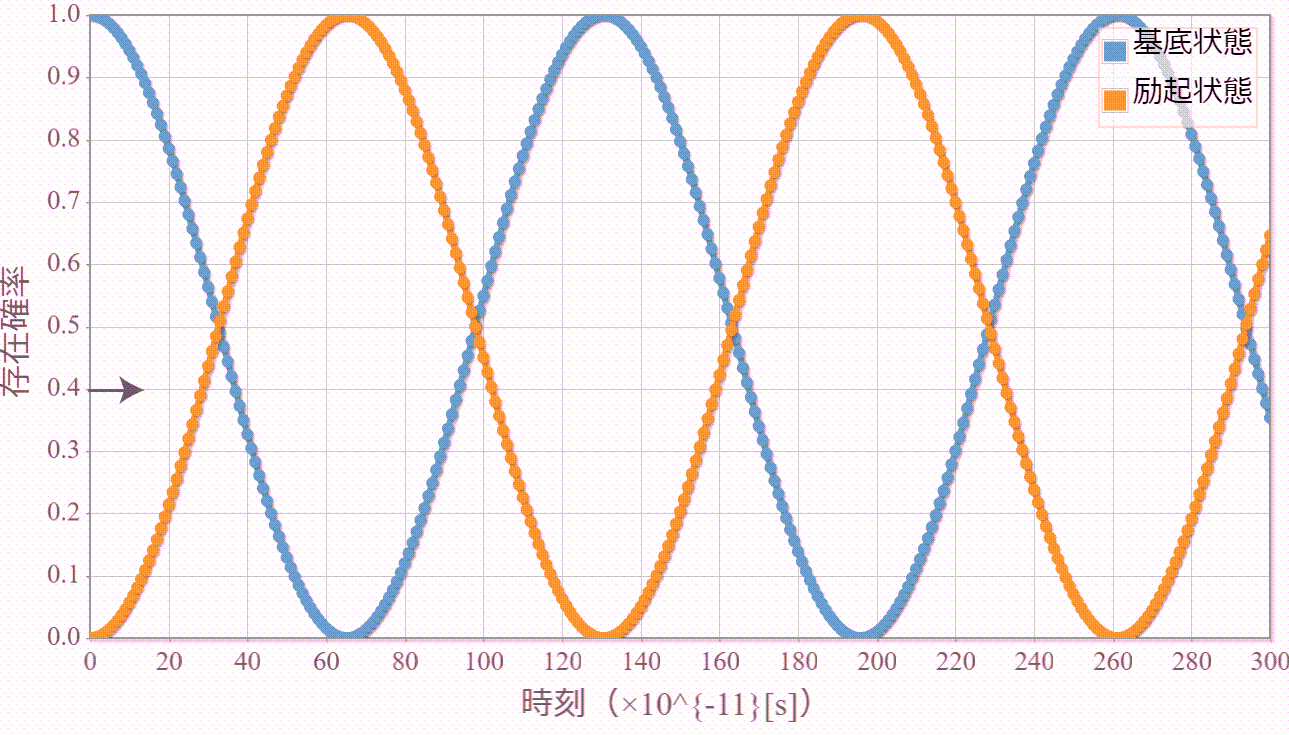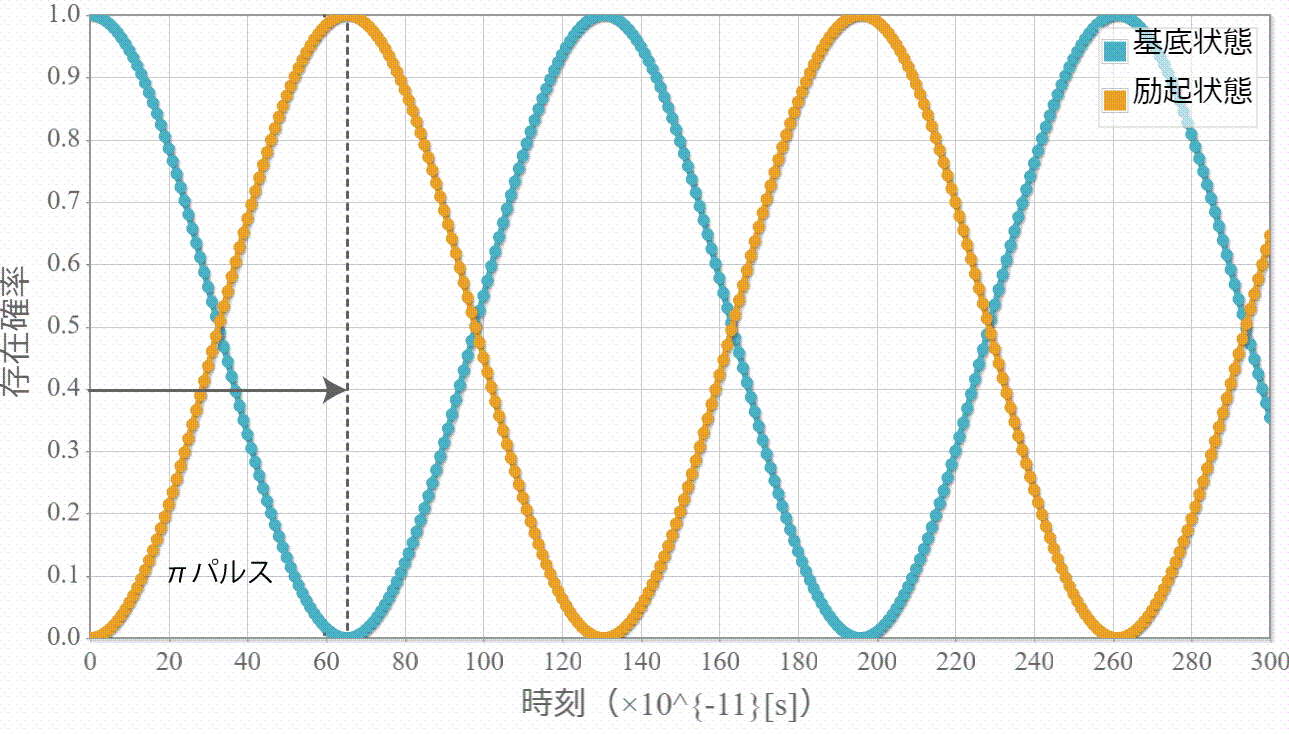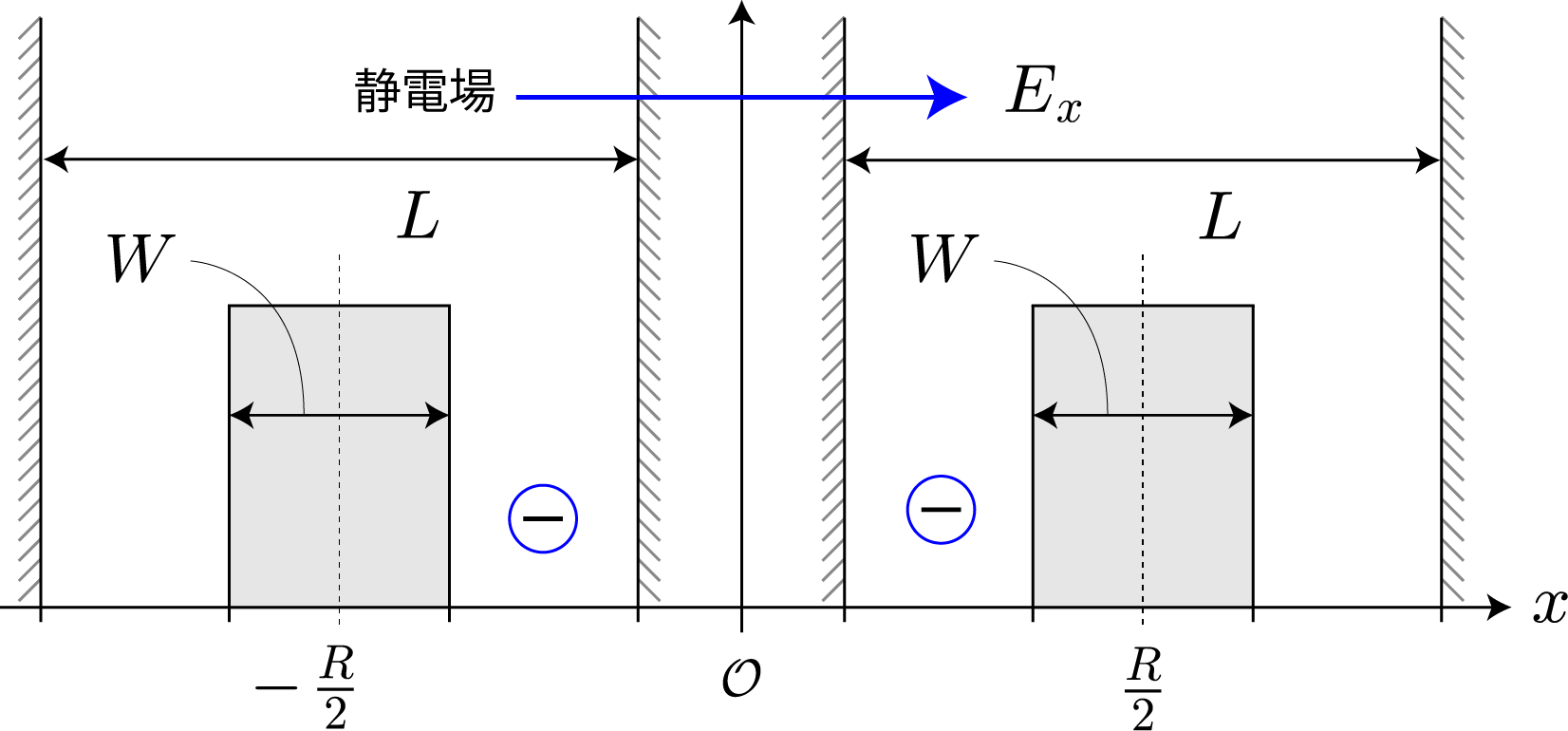
いよいよ最終目的の２量子ビットによる制御NOT演算を行うために、時間発展に必要なハミルトニアンの導出と計算方法を示すよ。復習から入っていくね。量子ビットを表す２つの量子井戸（幅：$L=10[{\rm nm}]$、高さ$+\infty$）はそれぞれが壁（幅： $W=L/5=2[{\rm nm}]$、高さ $V_0=0.3[{\rm eV}]$）で仕切られた２部屋になっていて、前々回と前回解説したとおり、２つの量子井戸の間隔 $R$ がちょうどよければ（$R=20[{\rm nm}]$）、電子間のクーロン相互作用が存在しても、電子は左右のどちらかに存在する状態を作り出せるね。そして、それぞれの量子井戸で左側に電子が存在する状態を $|0\rangle$、右側に電子が存在する場合を $|1\rangle$ と表わして、２電子の状態は $|00\rangle$、$|01\rangle$、$|10\rangle$、$|11\rangle$ の４パターンで表すよ。

定常状態のハミルトニアンと固有関数

この系の固有関数は、２つの量子井戸でそれぞれ定義される関数

\begin{align}
\varphi_{n_1}(x_1) &\ = \sqrt{\frac{2}{L}}\sin\left[ k_{n_1} \left( x_1 + \frac{R}{2} + \frac{L}{2}\right)\right] \ , \
k_{n_1} = \frac{\pi(n_1+1)}{L} \\
\varphi_{n_2}(x_2) &\ = \sqrt{\frac{2}{L}}\sin\left[ k_{n_2} \left( x_2 – \frac{R}{2} + \frac{L}{2}\right)\right] \ , \
k_{n_2} = \frac{\pi(n_2+1)}{L} \\
\end{align}

を用いたその積

\begin{align}
\varphi_{n_1n_2}(x_1, x_2) = \varphi_{n_1}(x_1)\varphi_{n_2}(x_2)
\end{align}

で表される正規直交系で展開することができるね。ちなみに単純な積で表されるのは２つの電子は交わらないからだよ。この２電子系の正規直交関数を用いて、次のように展開することができるね。

\begin{align}
\psi_{l_1l_2}(x_1, x_2) = \sum\limits_{n_1n_2} a^{(l_1l_2)}_{n_1n_2} \varphi_{n_1n_2}(x_1, x_2)
\end{align}

$l_1$ と $l_2$ は $0$ または $1$ のどちらかを取り、$\psi_{00}(x_1, x_2)$ は $|00\rangle$、$\psi_{01}(x_1, x_2)$ は $|01\rangle$、$\psi_{10}(x_1, x_2)$ は $|10\rangle$、$\psi_{11}(x_1, x_2)$ は $|11\rangle$ にそれぞれ対応した固有関数だよ。$a^{(l_1l_2)}_{n_1n_2}$ のように上付きのインデックス $l_1, l_2$ をつけたのはそれぞれの状態で展開係数の値が異なるので明示的につけているよ。この固有関数に対応するハミルトニアンは次のとおりだよ。

\begin{align}
\hat{H}^{(0)} = -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_1^2} + eE_xx_1 + V_1(x_1)-\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_2^2} + eE_xx_2 + V_2(x_2) + \frac{e^2}{4\pi\epsilon_0}\,\frac{1}{|x_1-x_2|}
\end{align}

$\hat{H}^{(0)}$ とインデックスに $(0)$ をつけているのは、前回すでに固有状態を計算できていて、次はこれに電磁波を加えることを想定しているからだよ。先の固有関数はこのハミルトニアンなので固有状態は

\begin{align}
\hat{H}^{(0)}\psi_{l_1l_2}(x_1, x_2) = E^{(0)}_{l_1l_2}\psi_{l_1l_2}(x_1, x_2)
\end{align}

と表されるよ。ここまでが前回の内容だね。ちなみに固有状態は

\begin{align}
\hat{H}^{(0)}|l_1l_2\rangle &\ = E^{(0)}_{l_1l_2}|l_1l_2\rangle \\
\langle l_1l_2| \hat{H}^{(0)} &\ = \langle l_1l_2|E^{(0)}_{l_1l_2}
\end{align}

とも表すことができるよ。これは後で使うね。

電磁波を入射したときのハミルトニアンと計算方法

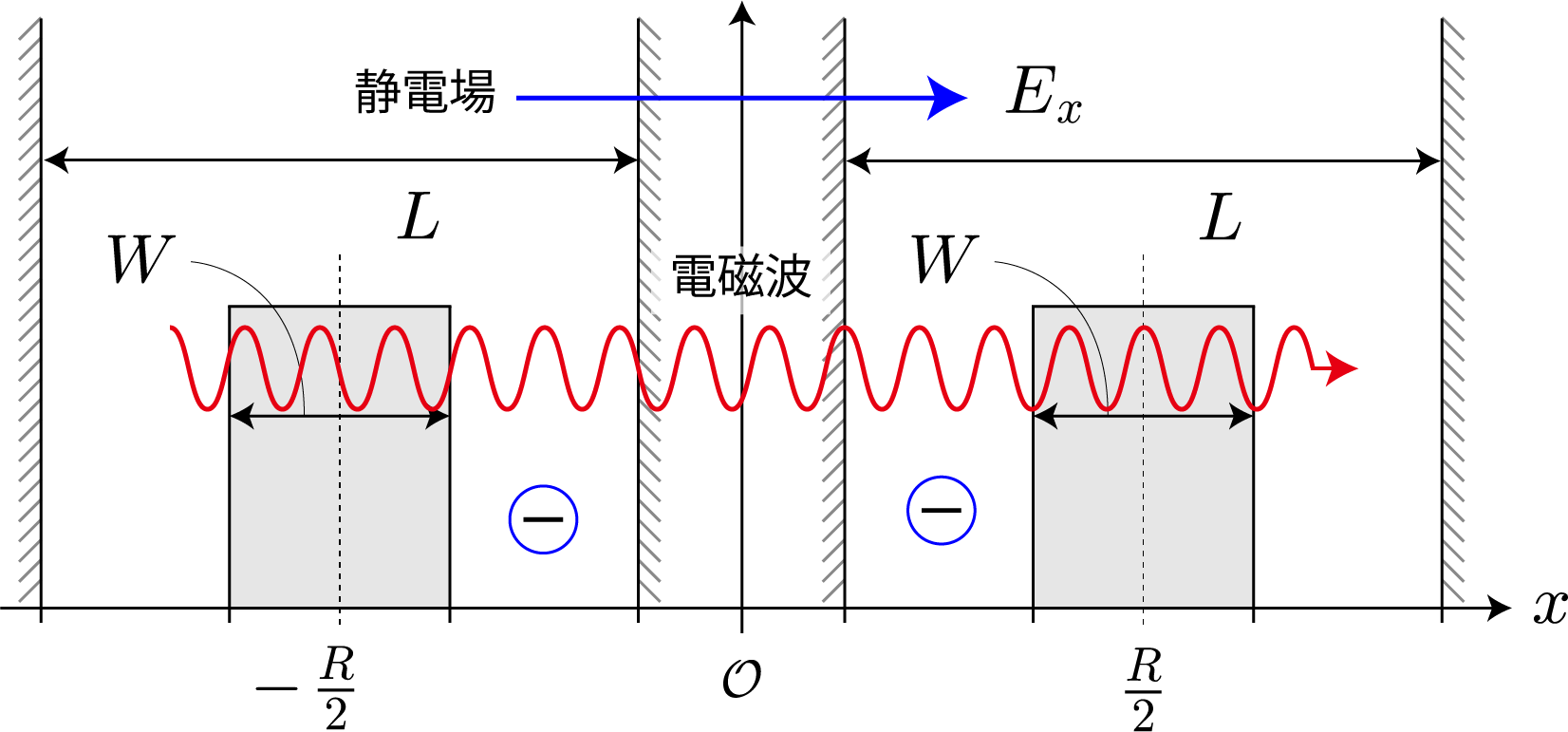
次に状態遷移を起こすために電磁波を加えるよ。ベクトルポテンシャルを $\boldsymbol{A}(t)$ としてハミルトニアンは

\begin{align}
\hat{H}(t) = \hat{H}^{(0)} + \frac{e}{m_e} \boldsymbol{A}(t)\cdot \hat{\boldsymbol{p}}_1 + \frac{e}{m_e} \boldsymbol{A}(t)\cdot \hat{\boldsymbol{p}}_2
\end{align}

となるね。今回も１次元系で考えているので、ベクトルポテンシャルを$\boldsymbol{A}(t) = (A_x(t), 0, 0)$ として、

\begin{align}
A_{x_1}(t) &\ = A_0 \cos(kx_1-\omega t)\\
A_{x_2}(t) &\ = A_0 \cos(kx_2-\omega t)
\end{align}

なので、ハミルトニアンは

\begin{align}
\hat{H}(t) = \hat{H}^{(0)} + \frac{e}{m_e} A_0 \left[ \cos(kx_1-\omega t)\hat{p}_{x_1} +\cos(kx_2-\omega t)\hat{p}_{x_2} \right]
\end{align}

となるね。このハミルトニアンは時間に依存するので固有状態は存在しないので、波動関数 $\Psi(t,x_1,x_2)$ を先の固有関数 $\psi_{l_1l_2}(x_1, x_2)$ で展開するよ。

\begin{align}
\Psi(t,x_1,x_2) = \sum\limits_{l_1 l_2} b_{l_1l_2}(t) \psi_{l_1l_2}(x_1, x_2)
\end{align}

$b_{l_1l_2}(t)$ が展開係数で、この展開係数が時間とともに変化するよ。時間に依存するシュレーディンガー方程式

\begin{align}
i\hbar \frac{\partial }{\partial t} \Psi(t,x_1,x_2)= \hat{H}(t) \Psi(t,x_1,x_2)
\end{align}

に代入して、両辺に $\psi_{m_1m_2}^*(x_1, x_2)$ を掛けて全空間で積分すると、次のような連立微分方程式になるよ。

\begin{align}
i\hbar \frac{d b_{m_1m_2}(t) }{d t} = E^{(0)}_{m_1m_2} b_{m_1m_2}(t) + e A_0 \sum\limits_{l_1 l_2} b_{l_1l_2}(t) \langle m_1 m_2| \left[\cos(kx_1-\omega t)\frac{\hat{p}_{x_1}}{m_e} + \cos(kx_2-\omega t)\frac{\hat{p}_{x_2}}{m_e}\right]| l_1l_2 \rangle
\end{align}

$\hat{p}_{x_1}/m_e = [\hat{H}^{(0)}, x_1 ]/i\hbar$、 $\hat{p}_{x_2}/m_e = [\hat{H}^{(0)}, x_2 ]/i\hbar$ の恒等式と長波長近似（$kx_1 = kx_2 \simeq 0$）を考慮すると次のようになるよ（特に長波長近似を課すことをしなくても数値計算自体は問題なくできるよ。でも表式が簡単になるね）。

\begin{align}
&\ \langle m_1 m_2| \left[\cos(kx_1-\omega t)\frac{\hat{p}_{x_1}}{m_e} + \cos(kx_2-\omega t)\frac{\hat{p}_{x_2}}{m_e}\right]| l_1l_2 \rangle\\
&\ =\frac{1}{i\hbar} \langle m_1 m_2| \left[\cos(kx_1-\omega t)\left(\hat{H}^{(0)}x_1 – x_1\hat{H}^{(0)}\right) + \cos(kx_2-\omega t)\left(\hat{H}^{(0)}x_2- x_2\hat{H}^{(0)}\right)\right]| l_1l_2 \rangle\\
&\ \simeq \frac{1}{i\hbar}\cos(\omega t)\langle m_1 m_2| \left[\hat{H}^{(0)}x_1 – x_1\hat{H}^{(0)} + \hat{H}^{(0)}x_2- x_2\hat{H}^{(0)}\right]| l_1l_2 \rangle\\
&\ = \frac{1}{i\hbar}\cos(\omega t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right) \langle m_1 m_2|(x_1 + x_2)| l_1l_2
\rangle \\
&\ = \frac{1}{i\hbar}\cos(\omega t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right) \int_{-\frac{R}{2}-\frac{L}{2}}^{-\frac{R}{2}+\frac{L}{2}} dx_1\int_{\frac{R}{2}-\frac{L}{2}}^{\frac{R}{2}+\frac{L}{2}}dx_2 \psi_{m_1m_2}^*(x_1, x_2)(x_1 + x_2)\psi_{l_1l_2}(x_1, x_2)\\
&\ \equiv \frac{1}{i\hbar}\cos(\omega t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right) K^{m_1m_2}_{l_1l_2}
\end{align}

この $K^{m_1m_2}_{l_1l_2}$ は時間に依存しないので１度計算すれば良いね。この $K^{m_1m_2}_{l_1l_2}$ を用いると先の連立微分方程式は次のようになるよ。

\begin{align}
i\hbar \frac{d b_{m_1m_2}(t) }{d t} = E^{(0)}_{m_1m_2} b_{m_1m_2}(t) + \frac{e A_0}{i\hbar} \cos(\omega t)　\sum\limits_{l_1 l_2} b_{l_1l_2}(t) \left( E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2} \right)K^{m_1m_2}_{l_1l_2}
\end{align}

電磁波の角振動数が２準位間のエネルギー差 $\Delta E = E^{(0)}_{m_1m_2} – E^{(0)}_{l_1l_2}$ と表して $\omega = \Delta E / \hbar$ となるときに、２準位間を周期的に遷移するね。$\Delta E = E^{(0)}_{11} – E^{(0)}_{10}$ を与えることで、制御・NOT演算となることを次回シミュレーションするよ。

今回から２量子ビットを作るための方法を考えていくね。本稿ではその第一歩として１個の量子ドットに２個の電子を投入したときの固有状態を計算するための計算方法を解説するよ。電子のようにスピンが1/2の粒子が複数個存在する場合、スピン座標を含めて波動関数の座標を交換すると反対称（符号が反転）することが知られているよ（ディラック方程式より）。スピンが1/2の電子のような粒子は、スピン演算子の特定成分の固有値が $\pm\hbar/2$ の２つのなるので、$+$ 符号を上向き、$-$ 符号を下向きと表すことが多いいね。２個の粒子のスピンが同じ向き（平行スピン）の場合には波動関数全体で反平行になる必要があるので空間部分は反対称になるのに対して、２個の粒子のスピンが反対向き（反平行スピン）の場合には空間部分は対称になる必要があるね。１粒子の波動関数をこれまでと同じ

\begin{align}
\varphi_n(x) = \sqrt{\frac{2}{L}} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ E^{(0)}_n = \frac{\hbar^2 k_n^2}{2m_e} \ , \ k_n = \frac{\pi(n+1)}{L}
\end{align}

と表した場合、２個の電子の空間対称関数（$\varphi^{(S)}$）と空間反対称関数（$\varphi^{(A)}$）は２つの電子位置を $x_1$ と $x_2$ として、それぞれ次のように表されるよ。

\begin{align}
\varphi^{(S)}_{n_1n_2}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1}(x_1)\varphi_{n_2}(x_2) + \varphi_{n_1}(x_2)\varphi_{n_2}(x_1) \right]\\
\varphi^{(A)}_{n_1n_2}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{n_1}(x_1)\varphi_{n_2}(x_2) – \varphi_{n_1}(x_2)\varphi_{n_2}(x_1) \right]
\end{align}

空間対称関数の場合、$x_1$ と $x_2$ を入替えても変化しないのに対して、空間反対称関数の場合、座標を入替えると符号がマイナスになるね。ただし、$n_1 = n_2$ の場合、空間対称関数の場合の係数は $1$ とする必要があることと、反対称関数の場合には関数値が $0$ になることに注意が必要だね。もし２個の電子が相互作用をしない場合、基底状態は空間対称関数（反平行スピン）で $n_1=n_2=0$ の場合だね。

\begin{align}
\varphi^{(S)}_{00}(x_1,x_2) = \varphi_{0}(x_1)\varphi_{0}(x_2)
\end{align}

第一励起状態は空間反対称関数（平行スピン）で $n_1=1, n_2=0$ あるいは $n_1=0, n_2=1$ の場合だね。

\begin{align}
\varphi^{(A)}_{10}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{1}(x_1)\varphi_{0}(x_2) – \varphi_{0}(x_2)\varphi_{1}(x_1) \right]\\
\varphi^{(A)}_{01}(x_1,x_2) &\ = \frac{1}{\sqrt{2}} \left[ \varphi_{0}(x_1)\varphi_{1}(x_2) – \varphi_{1}(x_2)\varphi_{0}(x_1) \right]
\end{align}

両者とも単に符号が反転しているだけなので、同じ関数を表しているよ。

電子間のクーロン力を考慮した場合のハミルトニアンと固有状態の計算方法

電子は同符号の電荷を持っているので互いに反発するね。そのため、基底状態は先に示したような簡単な形にはならないね。クーロン力を考慮した場合の２個の電子に対するハミルトニアンは次のとおりだよ。

\begin{align}
\hat{H} = \hat{H}_1 + \hat{H}_2 + V(|x_1-x_2|)= -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_1^2} -\frac{\hbar^2}{2m_e}\, \frac{\partial^2}{\partial x_2^2} + \frac{1}{4\pi\epsilon_0} \, \frac{1}{|x_1 – x_2|}
\end{align}

前の２項はそれぞれの電子の運動エネルギー、最後の項は相互作用を表しているね。このハミルトニアンの固有関数を $\psi^{(S)}(x_1, x_2)$（空間対称関数）、$\psi^{(A)}(x_1, x_2)$（空間反対称関数）と表した場合のシュレディンガー方程式は

\begin{align}
\hat{H} \psi^{(S)}(x_1, x_2) &\ = E \psi^{(S)}(x_1, x_2) \\
\hat{H} \psi^{(A)}(x_1, x_2) &\ = E \psi^{(A)}(x_1, x_2)
\end{align}

だね。この $\psi(x_1, x_2)$ は正規直交系である $\varphi^{(S)}_{n_1n_2}$ あるいは $\varphi^{(A)}_{n_1n_2}$ で展開できるはずなので、次のように表すことができるよ。

\begin{align}
\psi^{(S)}(x_1, x_2) &\ = \sum\limits_{n_1,n_2} a_{n_1n_2}\, \varphi^{(S)}_{n_1n_2}(x_1, x_2) \\
\psi^{(A)}(x_1, x_2) &\ = \sum\limits_{n_1,n_2} a_{n_1n_2}\, \varphi^{(A)}_{n_1n_2}(x_1, x_2)
\end{align}

ちなみに空間対称関数と反対称関数は直交するため混じり合うことは無いよ。ここからはいつもの常套手段でいくよ。この固有関数をハミルトニアンに代入して、両辺に $\varphi^{(S)*}_{n_1n_2}(x_1, x_2)$ あるいは $\varphi^{(A)*}_{m_1m_2}(x_1, x_2)$ を掛け算して全空間で積分すると

\begin{align}
a_{m_1m_2} ( E_{n_1}^{(0)} + E_{n_2}^{(0)}) + \sum\limits_{n_1,n_2} \langle m_1m_2|V(|x_1-x_2|)| n_1 n_2 \rangle a_{n_1n_2} = E a_{m_1m_2}
\end{align}

となるね。これは展開係数 $a_{m_1m_2}$ についての連立方程式となっているよ。対称性と反対称性の違いはブラ・ケット表記で表した積分

\begin{align}
\langle m_1m_2|V(|x_1-x_2|)| n_1 n_2 \rangle a_{n_1n_2} \equiv \left\{ \matrix{ \int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^{(S)*}_{m_1m_2}(x_1, x_2) V(|x_1-x_2|) \varphi^{(S)}_{n_1n_2}(x_1, x_2)dx_1dx_2 \cr \int_{-\frac{L}{2}}^{\frac{L}{2}}\int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^{(A)*}_{m_1m_2}(x_1, x_2) V(|x_1-x_2|) \varphi^{(A)}_{n_1n_2}(x_1, x_2)dx_1dx_2 } \right.
\end{align}

に違いが現れるね。次回は実際に固有状態を計算するよ。

追記：2019.07.16

同じ量子井戸に２個の電子を配置する場合、上記のような展開では積分が発散してしまうため、計算不能となってしまうね。発散を抑えられる正規直交展開にしないといけないけれども、どうしてもうまくいかないので、この方法は一度断念するね。

前回導出した２重量子ドットに束縛された電子の固有状態の計算方法を用いて計算した結果を示すよ。具体的なパラメータとして、量子井戸全体のサイズを $L = 10[{\rm nm}]$、真ん中の壁のサイズを $W = 2[{\rm nm}]$ として、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させてみたよ。まずは、固有状態から見てみよう！

固有状態の空間分布

基底状態

次の図は、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させたときの基底状態の空間分布だよ。壁の高さが高くなるほど電子分布のピークは両サイドの中心に移動していく様子が分かるね。ちなみに、基底状態の固有エネルギーは約 $0.004[{\rm eV}]$ だよ。

第一励起状態

次の図は、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させたときの第一励起状態の空間分布だよ。壁の高さが高くなるほど電子分布のピークは両サイドの中心に移動していくけれども、もともと第一励起状態は sin関数的なので変化は小さいね。ちなみに、基底状態の固有エネルギーは $0.015[{\rm eV}]$ 程度だよ。

第二励起状態

次の図は、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させたときの第二励起状態の空間分布だよ。基底状態と同様、壁の高さが高くなるほど電子分布のピークは両サイドの中心に移動していく様子が分かるね。ちなみに、基底状態の固有エネルギーは約 $0.034[{\rm eV}]$ だよ。

第三励起状態

次の図は、壁の高さを $0 \sim 0.5[{\rm eV}]$ と $0.025$ ずつ変化させたときの第三励起状態の空間分布だよ。第一励起状態と同様、壁の高さが高くなるほど電子分布のピークは両サイドの中心に移動していくけれども、もともと第三励起状態は sin関数的なので変化は小さいね。ちなみに、基底状態の固有エネルギーは約 $0.060[{\rm eV}]$ だよ。

エネルギー準位の壁の高さ依存性

先の固有状態からわかるとおり、壁の高さを高くするほど基底状態と第一励起状態、また第二励起状態と第三励起状態が一致していくね。これは、壁が高くなるほど、2つの領域はそれぞれ孤立していくことに起因するね。次の図は下から６つのエネルギー準位の壁の高さ依存性だけれども、このことはグラフにも現れているね。おおよそ壁の高さが $0.3[{\rm eV}]$ で基底状態と第一励起状態、第二励起状態と第三励起状態の固有エネルギーが概ね一致しているね。ちなみに、横の点線 $E_0=0.023[{\rm eV}]$ と $E_1=0.094[{\rm eV}]$ は、壁の高さが無限大とした場合の固有エネルギーの値だよ。

次回はさらに静電場を加えてみるよ。

まず、次の図は量子ドットに束縛された電子に $E_x = 2\times10^{6}[{rm eV}]$ の大きさの静電場を加えてることで変化した基底状態と励起状態だよ。基底状態は電場の向きの反対側に分布が偏って、励起状態は反対に電場の向きと同じ方向に分布が偏っているね。これは電気双極子が生じていると考えられるね。基底状態と励起状態の電気双極子はそれぞれ $\boldsymbol{p}_0 = -2e \langle \tilde0|x |\tilde0\rangle >0$ と $\boldsymbol{p}_1 = -2e \langle \tilde1|x |\tilde1\rangle< 0 $ となるよ。これらの電気双極子と静電場との相互作用によって、静電エネルギーは $ \Delta U = \boldsymbol{p} \cdot \boldsymbol{E} $ だけ変化するよ。さらに、この電気双極子によって生じる電場によって、外部から基底状態と励起状態のどちらの準位に存在するか測定することができるね。

次に、この２準位間のエネルギー差（$\Delta E = 0.01267 [{\rm eV}]$）に対応する光子エネルギーの電磁波（振動数：$f = 3.062 [{\rm THz}] $、波長：$\lambda = 97.90 [{\rm \mu m}] $）を入射して、２準位間のラビ振動をシミュレーションした結果を示すよ。想定通り、２準位間をsin関数的に遷移する様子が確認できたね。

量子ドットに束縛された電子に静電場を加えてることで変化した基底状態と第一励起状態に対して、外部から電磁波を与えて状態遷移の時間発展させることを考えるよ。静電場を加え無い場合と同様にラビ振動するはずだけれども、ちゃんとシミュレーションできるかどうかを確かめるよ。この場合のハミルトニアンは次のとおりだね。

\begin{align}
\hat{H} = -\frac{\hbar^2}{2m_e} \frac{d^2}{dx^2} + e E_x x + \frac{e}{m_e} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}
\end{align}

静磁場を加えたときの固有状態は数値的はすでに解けているので、そのハミルトニアンを $\hat{H}_{\rm Field}$ と表して、その固有関数を $\tilde{\varphi}_n(x)$、固有エネルギーを $\tilde{E}_n$ と表すと、次の固有方程式

\begin{align}
\hat{H}_{\rm Field} \tilde{\varphi}_n(x) = \tilde{E}_n\tilde{\varphi}_n(x)
\end{align}

を満たすね。ちなみに固有状態を明示的に表しておくと
\begin{align}
\tilde{\varphi}_n(x) = \sum\limits_{n’=0} a^{(n)}_{n’}\varphi_{n’}(x) = \sqrt{\frac{2}{L}} \sum\limits_{n’=0} a^{(n)}_{n’} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ k_n = \frac{\pi(n+1)}{L}
\end{align}

となって、この $a^{(n)}_{n’}$ が既知であるという意味だよ。このハミルトニアン $\hat{H}_{\rm Field}$ を用いて、元のハミルトニアンは

\begin{align}
\hat{H} = \hat{H}_{\rm Field} + \frac{e}{m_e} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}
\end{align}

と表すことができて、$\tilde{E}_n$ と $\tilde{\varphi}_n(x)$ はすでに既知なので、前回と同様にラビ振動をシミュレーションできそうだね。今回も１次元系で考えているので、ベクトルポテンシャルを $\boldsymbol{A}(t) = (A_x(t), 0, 0)$ として、

\begin{align}
A_x(t) = A_0 \cos(kx-\omega t)
\end{align}

と考えるよ。そして、電磁波を入射するときの波動関数を

\begin{align}
\tilde{\psi}(x, t) = \sum\limits_{n=0} \tilde{a}_n(t) \tilde{\varphi}_n(x)
\end{align}

という感じに、展開してその係数の値が時間に依存すると考えるよ。これを時間依存を考慮したシュレーディンガー方程式

\begin{align}
i \hbar \frac{\partial }{\partial t} \tilde{\psi}(x, t) = \hat{H} \tilde{\psi}(x, t)
\end{align}

に代入して、両辺に $\tilde{\varphi}^*_m(x)$ を掛けて全空間で積分するよ。すると、$\tilde{a}_m(t)$ に関する連立常微分方程式が得られるね。

\begin{align}
i \hbar \frac{d \tilde{a}_m(t)}{d t} = E^{(0)}_m \tilde{a}_m(t) + \sum\limits_{n=0} \langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle \tilde{a}_n(t)
\end{align}

$\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle$ は、

\begin{align}
\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \tilde{\varphi}^*_m(x) \hat{V}(t)
\tilde{\varphi}_n(x)\, dx = \sum\limits_{n’, m’=0} a^{(m)*}_{m’} a^{(n)}_{n’} \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_{m’}(x) \hat{V}(t)
\varphi_{n’}(x)\, dx = \sum\limits_{n’, m’=0} a^{(m)*}_{m’} a^{(n)}_{n’} \langle m’ | \hat{V}(t) | n’ \rangle
\end{align}

となって、静電場が無い場合の固有関数の積分の和で表すことができるね。$\hat{p}_x/m_e = [\hat{H}_0, x ]/i\hbar$ を考慮すると

\begin{align}
\langle m’ | \hat{V}(t) | n’ \rangle = \frac{1}{L}\int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_{m’}(x) \hat{V}(t)
\varphi_{n’}(x)\, dx = \frac{eA_0}{m_e} \langle m’ | \cos(kx-\omega t) p_x | n’ \rangle = \frac{eA_0}{i\hbar} \langle m’ | \cos(kx-\omega t) [\hat{H}_0, x ] | n’ \rangle
\end{align}

と変形できて、今回も波長が量子ドットのサイズよりも十分大きいと仮定すると、$kx \simeq 0$ と近似することができるので

\begin{align}
\langle m’ | \hat{V}(t) | n’ \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) \left[ E^{(0)}_{m’} – E^{(0)}_{n’} \right] \langle m’ |
x | n’ \rangle
\end{align}

となるので、最終的に $\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle$ は

\begin{align}
\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) \sum\limits_{n’, m’=0} a^{(m)*}_{m’} a^{(n)}_{n’} \left[ E^{(0)}_{m’} – E^{(0)}_{n’} \right] \langle m’ | x | n’ \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) K_{mn}
\end{align}

となるね。$K_{mn}$ は一度計算するれば良いので、これを用いて、展開係数$\tilde{a}_m(t)$ に関する連立常微分方程式は

\begin{align}
i \hbar \frac{d \tilde{a}_m(t)}{d t} = \tilde{E}_m \tilde{a}_m(t) + \frac{eA_0}{i\hbar} \cos(\omega t)\sum\limits_{n=0} K_{mn} a_n(t)
\end{align}

となるね。この $\tilde{E}_m, K_{mn}$ はあらかじめ計算することができるね。電磁波の角振動数が２準位間のエネルギー差 $\Delta E = \tilde{E}_1 – \tilde{E}_0$ と表して $\omega = \Delta E / \hbar$ となるときに、２準位間を周期的に遷移するね。次回はこれをシミュレーションするよ。

　量子コンピュータを勉強のために、シミュレーションが一番簡単そうな量子ドットに束縛された電子のエネルギー準位を量子ビットとして扱うタイプを念頭に置いて、量子コンピュータを実現するために必要な素子の具体的な物理系のシミュレーション（数値実験）を行っていくよ。今回は、１次元版量子ドット（井戸型ポテンシャル）に束縛された電子の状態を変化させるために静電場を加えたときの固有状態を調べるよ。

静電場を加えたハミルトニアンとシュレディンガー方程式

井戸型ポテンシャルに束縛された電子に外部からx軸方向の静電場 $E_x$ を加えると、電子は静電場によって空間分布が変化することが考えられるね。量子井戸の底のポテンシャルエネルギーを０としたときのハミルトニアンは次のとおりだね。

\begin{align}
\hat{H} = \hat{H}_0 + \hat{V} = -\frac{\hbar^2}{2m_e} \frac{d^2}{dx^2} – e E_x x \\
\end{align}

$\hat{V}$ は静電場によるポテンシャルエネルギーだよ。$\hat{H}_0$ は 外場無し（$E_x = 0$）のときのハミルトニアンで、井戸の深さが無限大のときには固有関数 $\varphi_n(x)$ を用いて、エネルギー固有状態 $\hat{H}_0 \varphi_n(x) = E_n \varphi_n(x)$ を満たすよ。固有関数と固有エネルギーは

\begin{align}
\varphi_n(x) = \sqrt{\frac{2}{L}} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ E_n = \frac{\hbar^2 k_n^2}{2m_e} \ , \ k_n = \frac{\pi(n+1)}{L}
\end{align}

だね。$k_n$ は波数だよ。静磁場が加わったときの固有関数と固有エネルギーをそれぞれ $\varphi(x)$ と $E$ と表したとき、シュレディンガー方程式は

\begin{align}
\hat{H} \varphi(x)= E \varphi(x) \\
\end{align}

となるけれど、この $\varphi(x)$ を $\varphi_n(x)$ を用いて

\begin{align}
\varphi(x) = \sum\limits_{n=0} a_n \varphi_n(x)
\end{align}

と展開して、固有関数と固有エネルギーを計算するよ。

固有関数と固有エネルギーの計算方法

シュレディンガー方程式の両辺に $\varphi^*_m(x)$ を掛けて全空間で積分するよ。固有関数の直交関係を考慮すると、シュレディンガー方程式は

\begin{align}
E^{(0)}_m a_m + \sum\limits_{n=0} \langle m | \hat{V} | n \rangle a_n = E a_m
\end{align}

という展開係数 $ a_n $ に関する連立方程式になるね。ただし、$\langle m | \hat{V} | n \rangle $ は

\begin{align}
\langle m | \hat{V} | n \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_m(x) \hat{V} \varphi_n(x)\, dx
\end{align}

だよ。連立方程式は行列で表すとわかりやすくなるので、エネルギーの小さい順に固有関数の係数を並べると次のようになるよ。

\begin{align}
\left(\matrix{ E^{(0)}_0 +\langle 0 | \hat{V} | 0 \rangle & \langle 1 | \hat{V} | 0 \rangle & \langle 2 | \hat{V} | 0 \rangle & \langle 3 | \hat{V} | 0 \rangle & \langle 4 | \hat{V} | 0 \rangle & \cdots \cr
\langle 0 | \hat{V} | 1 \rangle & E^{(0)}_1 + \langle 1 | \hat{V} | 1 \rangle & \langle 1 | \hat{V} | 2 \rangle & \langle 1 | \hat{V} | 3 \rangle &\langle 1 | \hat{V} | 4 \rangle &\cdots \cr
\langle 0 | \hat{V} | 2 \rangle & \langle 1 | \hat{V} | 2 \rangle & E^{(0)}_2 + \langle 2 | \hat{V} | 2 \rangle & \langle 3 | \hat{V} | 2 \rangle& \langle 4 | \hat{V} | 2 \rangle& \cdots \cr
\langle 0 | \hat{V} | 3 \rangle & \langle 1 | \hat{V} | 3 \rangle & \langle 2 | \hat{V} | 3 \rangle & E^{(0)}_3 + \langle 3 | \hat{V} | 3 \rangle& \langle 4 | \hat{V} | 3 \rangle& \cdots \cr
\langle 0 | \hat{V} | 4 \rangle & \langle 1 | \hat{V} | 4 \rangle & \langle 2 | \hat{V} | 4 \rangle & \langle 3 | \hat{V} | 4 \rangle& E^{(0)}_4 + \langle 4 | \hat{V} | 4 \rangle& \cdots \cr
\vdots & \vdots & \vdots & \vdots & \vdots & \ddots } \right) \left(\matrix{ a_{0} \cr a_{1}\cr a_{2} \cr a_{3} \cr a_{4} \cr \vdots }\right) = E \left(\matrix{ a_{0} \cr a_{1}\cr a_{2} \cr a_{3} \cr a_{4} \cr \vdots }\right)
\end{align}

まさに行列表した固有値方程式の形になっているのがわかるね。 これで固有値と固有ベクトルを計算すると、固有値はそのまま外場が加えられた場合のエネルギー、固有ベクトルがそのまま展開係数の値そのものになるね。次回は、この計算結果を示すよ。