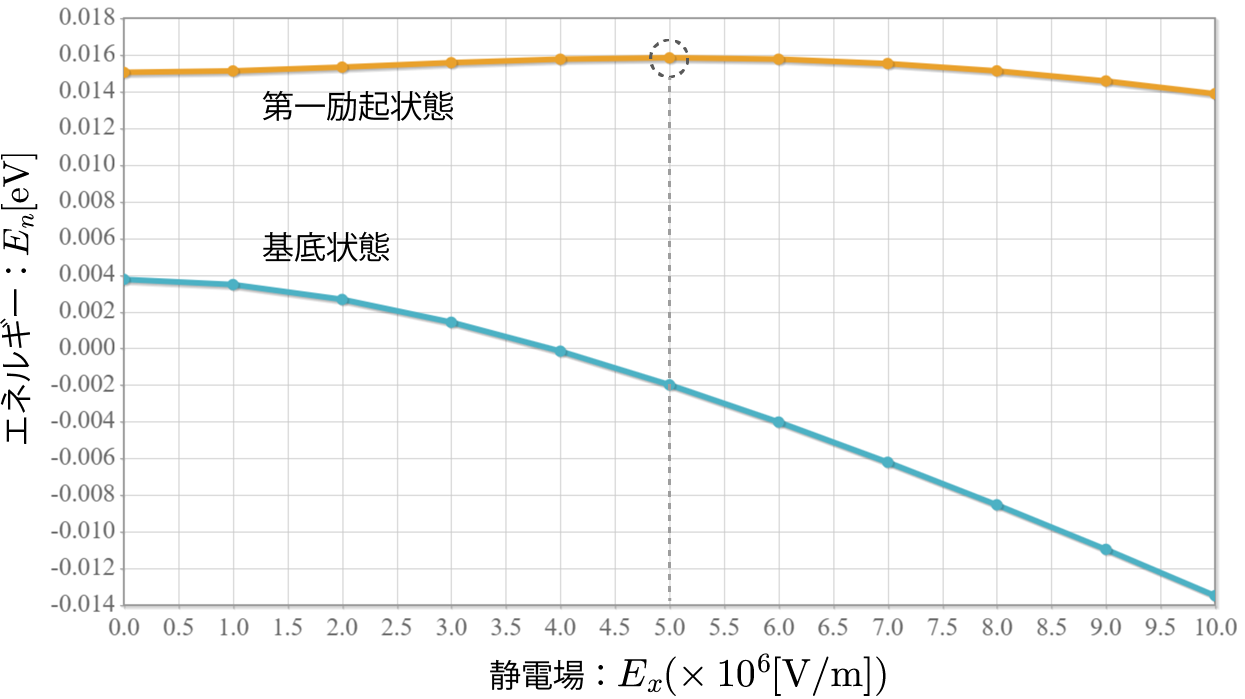
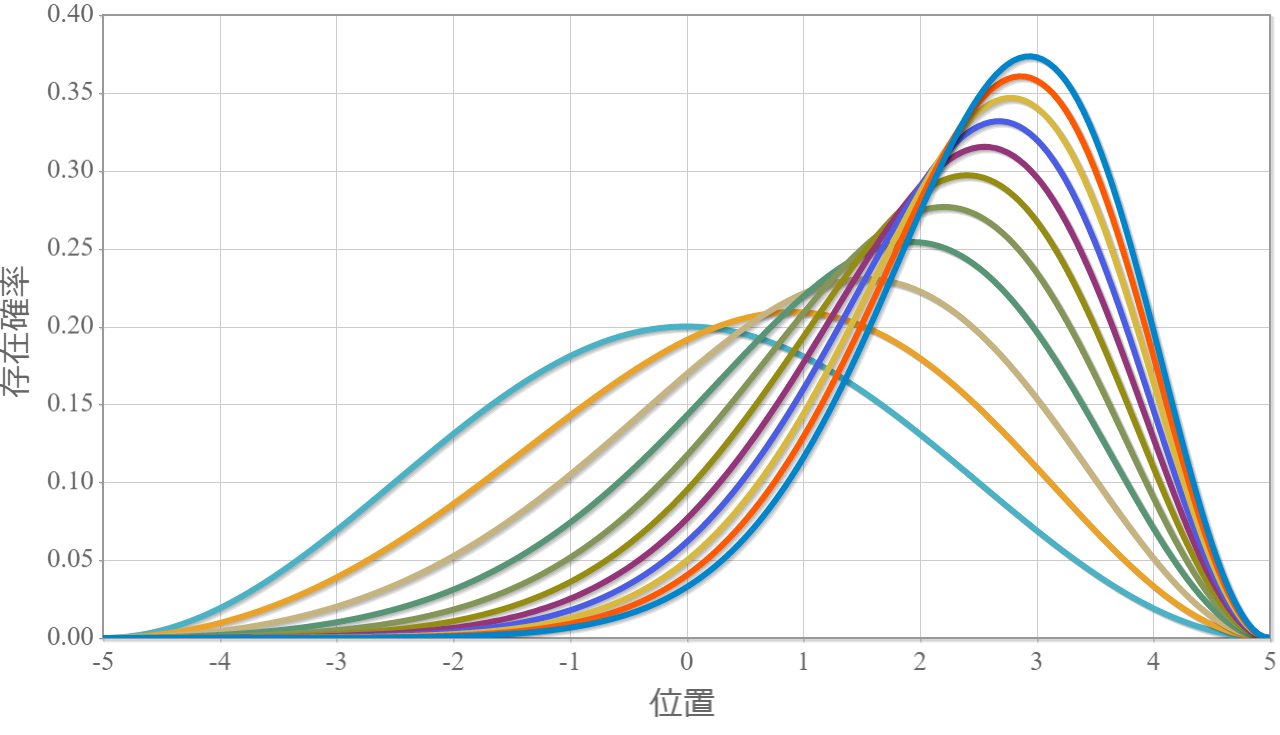
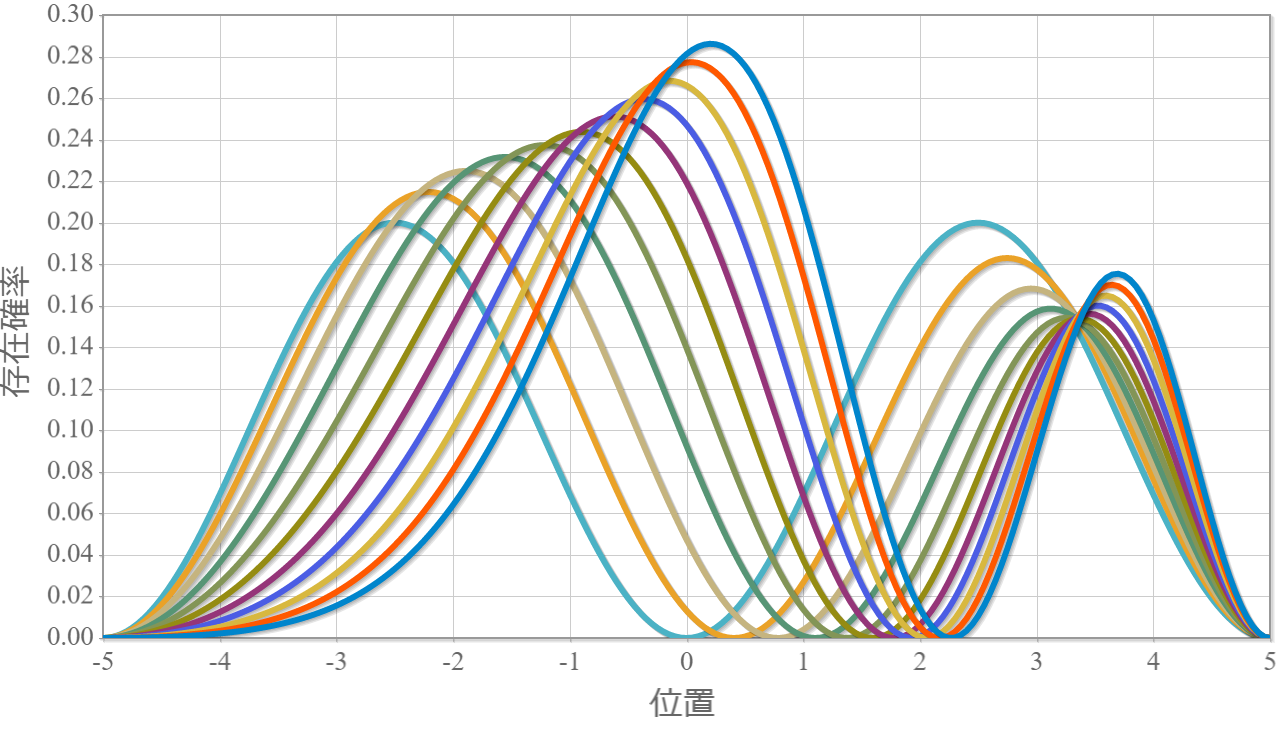
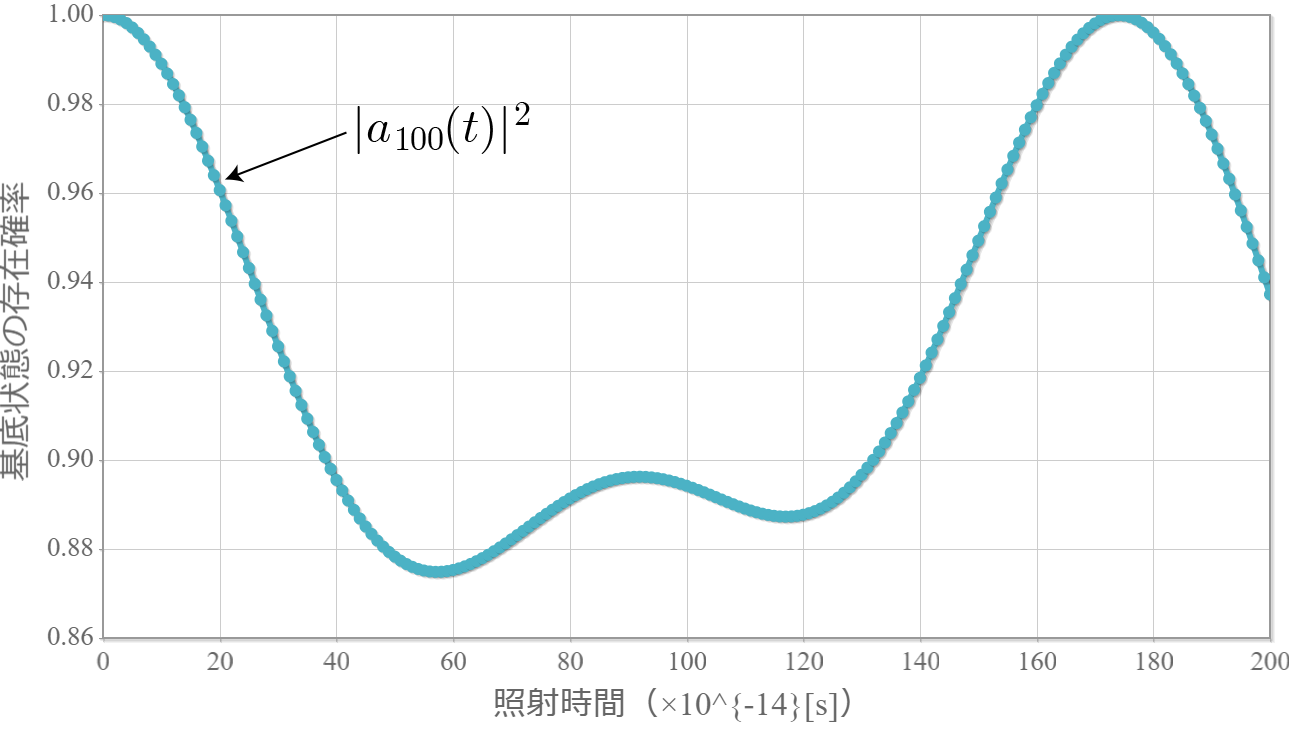
量子ドットに束縛された電子に静電場を加えてることで変化した基底状態と第一励起状態に対して、外部から電磁波を与えて状態遷移の時間発展させることを考えるよ。静電場を加え無い場合と同様にラビ振動するはずだけれども、ちゃんとシミュレーションできるかどうかを確かめるよ。この場合のハミルトニアンは次のとおりだね。
\begin{align}
\hat{H} = -\frac{\hbar^2}{2m_e} \frac{d^2}{dx^2} + e E_x x + \frac{e}{m_e} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}
\end{align}
静磁場を加えたときの固有状態は数値的はすでに解けているので、そのハミルトニアンを $\hat{H}_{\rm Field}$ と表して、その固有関数を $\tilde{\varphi}_n(x)$、固有エネルギーを $\tilde{E}_n$ と表すと、次の固有方程式
\begin{align}
\hat{H}_{\rm Field} \tilde{\varphi}_n(x) = \tilde{E}_n\tilde{\varphi}_n(x)
\end{align}
を満たすね。ちなみに固有状態を明示的に表しておくと
\begin{align}
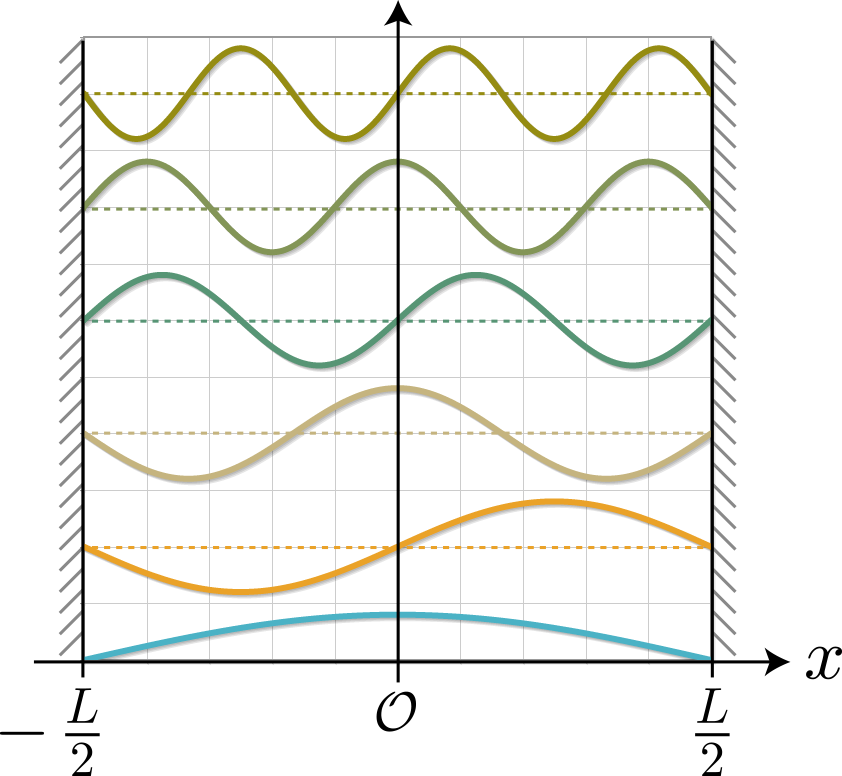
\tilde{\varphi}_n(x) = \sum\limits_{n’=0} a^{(n)}_{n’}\varphi_{n’}(x) = \sqrt{\frac{2}{L}} \sum\limits_{n’=0} a^{(n)}_{n’} \sin\left[ k_n (x + \frac{L}{2}) \right] \ , \ k_n = \frac{\pi(n+1)}{L}
\end{align}
となって、この $a^{(n)}_{n’}$ が既知であるという意味だよ。このハミルトニアン $\hat{H}_{\rm Field}$ を用いて、元のハミルトニアンは
\begin{align}
\hat{H} = \hat{H}_{\rm Field} + \frac{e}{m_e} \boldsymbol{A}\cdot \hat{\boldsymbol{p}}
\end{align}
と表すことができて、$\tilde{E}_n$ と $\tilde{\varphi}_n(x)$ はすでに既知なので、前回と同様にラビ振動をシミュレーションできそうだね。今回も1次元系で考えているので、ベクトルポテンシャルを $\boldsymbol{A}(t) = (A_x(t), 0, 0)$ として、
\begin{align}
A_x(t) = A_0 \cos(kx-\omega t)
\end{align}
と考えるよ。そして、電磁波を入射するときの波動関数を
\begin{align}
\tilde{\psi}(x, t) = \sum\limits_{n=0} \tilde{a}_n(t) \tilde{\varphi}_n(x)
\end{align}
という感じに、展開してその係数の値が時間に依存すると考えるよ。これを時間依存を考慮したシュレーディンガー方程式
\begin{align}
i \hbar \frac{\partial }{\partial t} \tilde{\psi}(x, t) = \hat{H} \tilde{\psi}(x, t)
\end{align}
に代入して、両辺に $\tilde{\varphi}^*_m(x)$ を掛けて全空間で積分するよ。すると、$\tilde{a}_m(t)$ に関する連立常微分方程式が得られるね。
\begin{align}
i \hbar \frac{d \tilde{a}_m(t)}{d t} = E^{(0)}_m \tilde{a}_m(t) + \sum\limits_{n=0} \langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle \tilde{a}_n(t)
\end{align}
$\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle$ は、
\begin{align}
\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle \equiv \int_{-\frac{L}{2}}^{\frac{L}{2}} \tilde{\varphi}^*_m(x) \hat{V}(t)
\tilde{\varphi}_n(x)\, dx = \sum\limits_{n’, m’=0} a^{(m)*}_{m’} a^{(n)}_{n’} \int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_{m’}(x) \hat{V}(t)
\varphi_{n’}(x)\, dx = \sum\limits_{n’, m’=0} a^{(m)*}_{m’} a^{(n)}_{n’} \langle m’ | \hat{V}(t) | n’ \rangle
\end{align}
となって、静電場が無い場合の固有関数の積分の和で表すことができるね。$\hat{p}_x/m_e = [\hat{H}_0, x ]/i\hbar$ を考慮すると
\begin{align}
\langle m’ | \hat{V}(t) | n’ \rangle = \frac{1}{L}\int_{-\frac{L}{2}}^{\frac{L}{2}} \varphi^*_{m’}(x) \hat{V}(t)
\varphi_{n’}(x)\, dx = \frac{eA_0}{m_e} \langle m’ | \cos(kx-\omega t) p_x | n’ \rangle = \frac{eA_0}{i\hbar} \langle m’ | \cos(kx-\omega t) [\hat{H}_0, x ] | n’ \rangle
\end{align}
と変形できて、今回も波長が量子ドットのサイズよりも十分大きいと仮定すると、$kx \simeq 0$ と近似することができるので
\begin{align}
\langle m’ | \hat{V}(t) | n’ \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) \left[ E^{(0)}_{m’} – E^{(0)}_{n’} \right] \langle m’ |
x | n’ \rangle
\end{align}
となるので、最終的に $\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle$ は
\begin{align}
\langle \tilde{m} | \hat{V}(t) | \tilde{n} \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) \sum\limits_{n’, m’=0} a^{(m)*}_{m’} a^{(n)}_{n’} \left[ E^{(0)}_{m’} – E^{(0)}_{n’} \right] \langle m’ | x | n’ \rangle = \frac{eA_0}{i\hbar} \cos(\omega t) K_{mn}
\end{align}
となるね。$K_{mn}$ は一度計算するれば良いので、これを用いて、展開係数$\tilde{a}_m(t)$ に関する連立常微分方程式は
\begin{align}
i \hbar \frac{d \tilde{a}_m(t)}{d t} = \tilde{E}_m \tilde{a}_m(t) + \frac{eA_0}{i\hbar} \cos(\omega t)\sum\limits_{n=0} K_{mn} a_n(t)
\end{align}
となるね。この $\tilde{E}_m, K_{mn}$ はあらかじめ計算することができるね。電磁波の角振動数が2準位間のエネルギー差 $\Delta E = \tilde{E}_1 – \tilde{E}_0$ と表して $\omega = \Delta E / \hbar$ となるときに、2準位間を周期的に遷移するね。次回はこれをシミュレーションするよ。